19 KiB

Raw Blame History Unescape Escape

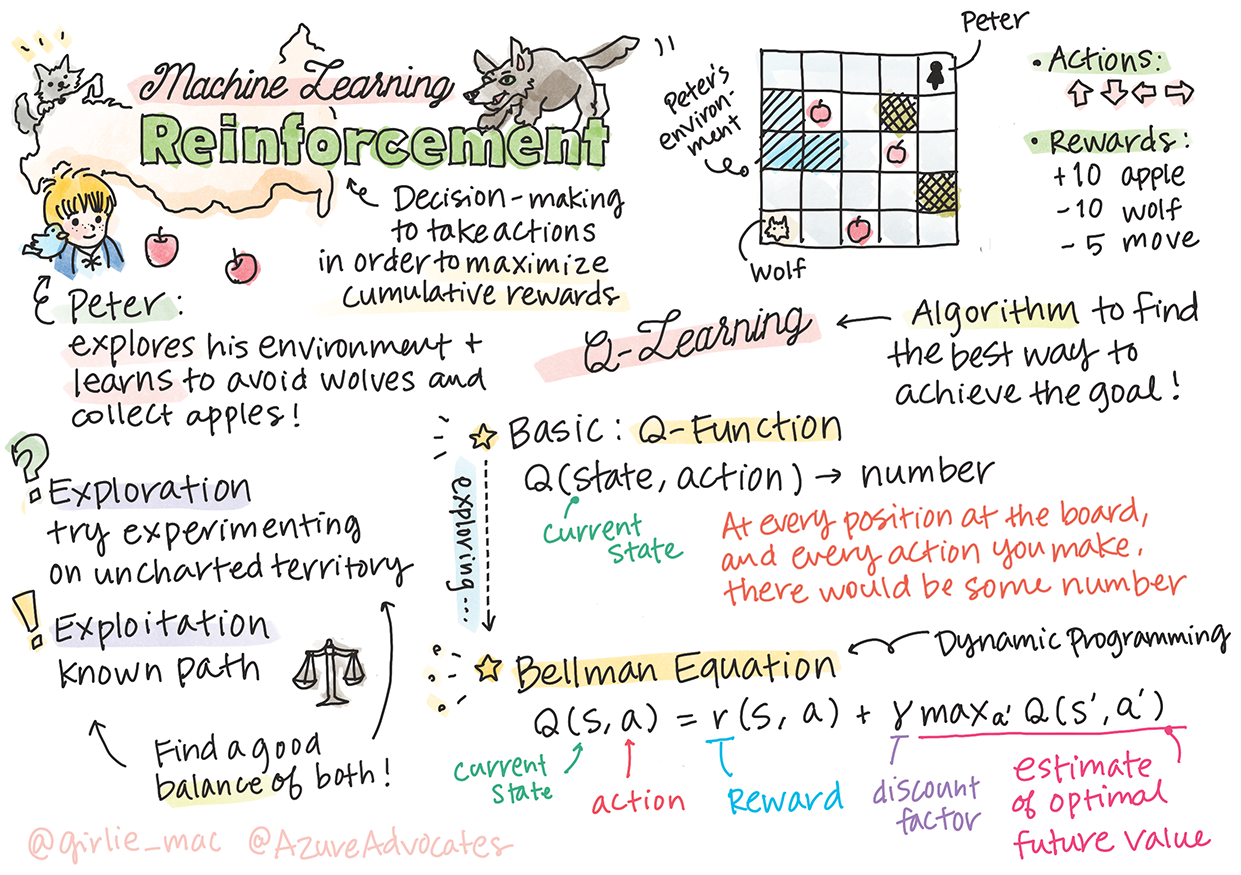
Reinforcement Learning과 Q-Learning 소개하기

Sketchnote by Tomomi Imura

Reinforcement learning에는 3가지 중요한 컨셉이 섞여있습니다: agent, 일부 states, 그리고 state 당 actions 세트. 특정 상황에서 행동하면 agent에게 보상이 주어집니다. Super Mario 게임을 다시 상상해봅니다. 마리오가 되어서, 게임 레벨에 진입하고, 구덩이 옆에 있습니다. 그 위에 동전이 있습니다. 게임 레벨에서, 특정 위치에 있는, 마리오가 됩니다 ... 이게 state 입니다. 한 단계 오른쪽으로 이동하면 (action) 구덩이를 빠져서, 낮은 점수를 받습니다. 그러나, 점프 버튼을 누르면 점수를 얻고 살아남을 수 있습니다. 긍정적인 결과이며, 긍정적인 점수를 줘야 합니다.

reinforcement learning과 (게임) 시뮬레이터로, 살아남고 가능한 많은 점수로 최대 보상을 받는 게임의 플레이 방식을 배울 수 있습니다.

🎥 Dmitry discuss Reinforcement Learning 들으려면 이미지 클릭

강의 전 퀴즈

전제조건 및 설정

이 강의에서, Python으로 약간의 코드를 실험할 예정입니다. 이 강의에서 Jupyter Notebook을, 컴퓨터나 클라우드 어디에서나 실행해야 합니다.

the lesson notebook을 열고 이 강의로 만들 수 있습니다.

노트: 만약 클라우드에서 코드를 연다면, 노트북 코드에서 사용하는 rlboard.py 파일도 가져올 필요가 있습니다. 노트북과 같은 디렉토리에 추가합니다.

소개

이 강의에서, 러시아 작곡가 Sergei Prokofiev의 동화 곡에 영감을 받은, Peter and the Wolf 의 월드를 탐험해볼 예정입니다. Reinforcement Learning으로 Peter가 환경을 탐험하고, 맛있는 사과를 모으고 늑대는 피할 것입니다.

Reinforcement Learning (RL)은 많은 실험을 돌려서 일부 environment에서 agent의 최적화된 동작을 배울 수 있는 훈련 기술입니다. 이 환경의 agent는 reward function으로 정의된, 약간의 goal을 가지고 있어야 합니다.

환경

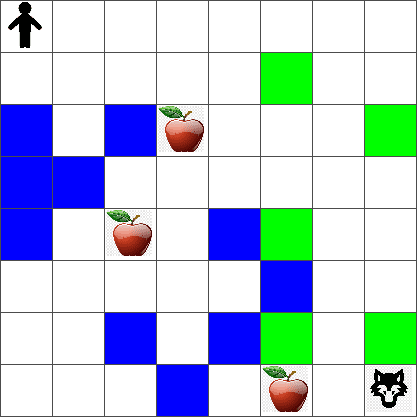
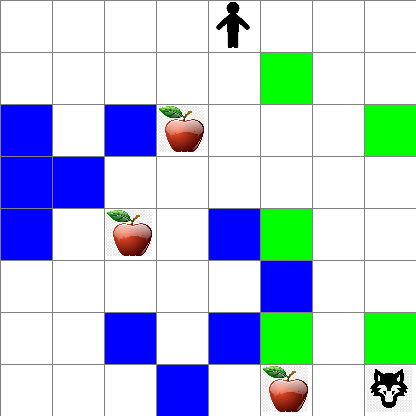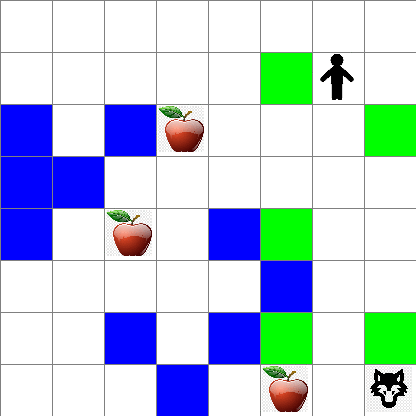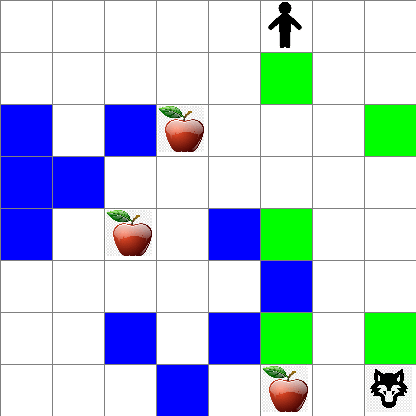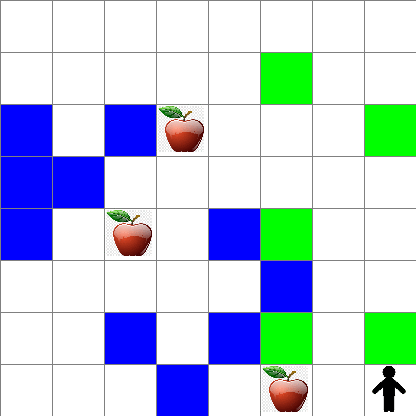
단순하고자, Peter의 월드를 이렇게 width x height 크기의 정사각형 보드로 고려해보려 합니다:

이 보드에서 각 셀은 이 중 하나 입니다:

ground, Peter와 다른 생명체가 걸을 수 있습니다.
water, 무조건 걸을 수 없습니다.
a tree or grass, 휴식할 수 있는 장소입니다.
an apple, Peter가 스스로 먹으려고 찾을 수 있는 물건입니다.
a wolf, 위험하고 피해야 합니다.

이 환경에서 작성하는 코드가 포함되어 있는, rlboard.py 별도 Python 모듈이 있습니다. 그러므로 이 코드는 컨셉을 이해하는 게 중요하지 않으므로, 모듈을 가져오고 샘플 보드를 (code block 1) 만들고자 사용할 예정입니다:

from rlboard import *

width, height = 8,8
m = Board(width,height)
m.randomize(seed=13)
m.plot()

이 코드는 위와 비슷하게 그림을 출력하게 됩니다.

액션과 정책

예시에서, Peter의 목표는 늑대와 장애물을 피하고, 사과를 찾는 것입니다. 그러기 위해서, 사과를 찾기 전까지 걷게 됩니다.

그러므로, 어느 위치에서, 다음 액션 중 하나를 선택할 수 있습니다: up, down, left 그리고 right.

이 액션을 dictionary로 정의하고, 좌표 변경의 쌍을 맵핑합니다. 오른쪽 이동(R)은 (1,0) 쌍에 대응합니다. (code block 2):

actions = { "U" : (0,-1), "D" : (0,1), "L" : (-1,0), "R" : (1,0) }
action_idx = { a : i for i,a in enumerate(actions.keys()) }

요약해보면, 이 시나리오의 전략과 목표는 다음과 같습니다:

agent (Peter)의 전략은, policy로 불리며 정의됩니다. 정책은 주어진 state에서 action을 반환하는 함수입니다. 이 케이스에서, 문제의 state는 플레이어의 현재 위치를 포함해서, 보드로 표현합니다.
reinforcement learning의 목표는, 결국 문제를 효율적으로 풀수 있게 좋은 정책을 학습하는 것입니다. 그러나, 기본적으로, random walk라고 불리는 단순한 정책을 고려해보겠습니다.

랜덤 워킹

랜덤 워킹 전략으로 첫 문제를 풀어봅시다. 랜덤 워킹으로, 사과에 닿을 때까지, 허용된 액션에서 다음 액션을 무작위로 선택합니다 (code block 3).

아래 코드로 랜덤 워킹을 구현합니다:

def random_policy(m):
    return random.choice(list(actions))

def walk(m,policy,start_position=None):
    n = 0 # number of steps
    # set initial position
    if start_position:
        m.human = start_position 
    else:
        m.random_start()
    while True:
        if m.at() == Board.Cell.apple:
            return n # success!
        if m.at() in [Board.Cell.wolf, Board.Cell.water]:
            return -1 # eaten by wolf or drowned
        while True:
            a = actions[policy(m)]
            new_pos = m.move_pos(m.human,a)
            if m.is_valid(new_pos) and m.at(new_pos)!=Board.Cell.water:
                m.move(a) # do the actual move
                break
        n+=1

walk(m,random_policy)

walk를 부르면 실행할 때마다 다르게, 일치하는 경로의 길이를 반환합니다.

워킹 실험을 여러 번 (say, 100) 실행하고, 통계 결과를 출력합니다 (code block 4):

def print_statistics(policy):
    s,w,n = 0,0,0
    for _ in range(100):
        z = walk(m,policy)
        if z<0:
            w+=1
        else:
            s += z
            n += 1
    print(f"Average path length = {s/n}, eaten by wolf: {w} times")

print_statistics(random_policy)

가까운 사과으로 가는 평균 걸음이 대략 5-6 걸음이라는 사실로 주어졌을 때, 경로의 평균 길이가 대략 30-40 걸음이므로, 꽤 오래 걸립니다.

또 랜덤 워킹을 하는 동안 Peter의 행동이 어떻게 되는지 확인할 수 있습니다:

보상 함수

정책을 더 지능적으로 만드려면, 행동을 다른 것보다 "더" 좋은지 이해할 필요가 있습니다. 이렇게, 목표를 정의할 필요가 있습니다.

목표는 각 state에서 일부 점수 값을 반환할 예정인, reward function로 정의할 수 있습니다. 높은 점수일수록, 더 좋은 보상 함수입니다. (code block 5)

move_reward = -0.1
goal_reward = 10
end_reward = -10

def reward(m,pos=None):
    pos = pos or m.human
    if not m.is_valid(pos):
        return end_reward
    x = m.at(pos)
    if x==Board.Cell.water or x == Board.Cell.wolf:
        return end_reward
    if x==Board.Cell.apple:
        return goal_reward
    return move_reward

보상 함수에 대해서 흥미로운 것은 많은 경우에, 게임이 끝날 때만 중요한 보상을 줍니다. 알고리즘이 끝날 때 긍정적인 보상으로 이어지는 "good" 단계를 어떻게든지 기억하고, 중요도를 올려야 된다는 점을 의미합니다. 비슷하게, 나쁜 결과를 이끄는 모든 동작을 하지 말아야 합니다.

Q-Learning

여기에서 논의할 알고리즘은 Q-Learning이라고 불립니다. 이 알고리즘에서, 정책은 Q-Table 불리는 함수 (데이터 구조)로 정의합니다. 주어진 state에서 각 액션의 "goodness"를 기록합니다.

테이블, 또는 multi-dimensional 배열로 자주 표현하는 게 편리하므로 Q-Table이라고 부릅니다. 보드는 width x height 크기라서, width x height x len(actions) 형태의 numpy 배열로 Q-Table을 표현할 수 있습니다 : (code block 6)

Q = np.ones((width,height,len(actions)),dtype=np.float)*1.0/len(actions)

Q-Table의 모든 값이 같다면, 이 케이스에서 - 0.25 으로 초기화합니다. 각자 state는 모두가 충분히 동일하게 움직이므로, "random walk" 정책에 대응됩니다. 보드에서 테이블을 시각화하기 위해서 Q-Table을 plot 함수에 전달할 수 있습니다: m.plot(Q).

각자 셀의 중심에 이동하는 방향이 표시되는 "arrow"가 있습니다. 모든 방향은 같으므로, 점이 출력됩니다.

사과로 가는 길을 더 빨리 찾을 수 있으므로, 지금부터 시물레이션을 돌리고, 환경을 찾고, 그리고 더 좋은 Q-Table 분포 값을 배울 필요가 있습니다.

Q-Learning의 핵심: Bellman 방정식

움직이기 시작하면, 각 액션은 알맞은 보상을 가집니다, 예시로. 이론적으로 가장 높은 보상을 바로 주면서 다음 액션을 선택할 수 있습니다. 그러나, 대부분 state 에서, 행동은 사과에 가려는 목표가 성취감에 없으므로, 어떤 방향이 더 좋은지 바로 결정하지 못합니다.

즉시 발생되는 결과가 아니라, 시뮬레이션의 끝에 도달했을 때 생기는, 최종 결과라는 것을 기억합니다.

딜레이된 보상에 대해 설명하려면, 문제를 재귀적으로 생각할 수 있는, dynamic programming 의 원칙을 사용할 필요가 있습니다.

지금 state s에 있고, state s' 다음으로 움직이길 원한다고 가정합니다. 그렇게 하면, 보상 함수로 정의된 즉시 보상 r(s,a) 를 일부 미래 보상과 함께 받게 될 예정입니다. Q-Table이 각 액션의 "attractiveness"를 올바르게 가져온다고 가정하면, s' state에서 Q(s',a') 의 최대 값에 대응하는 a 액션을 선택하게 됩니다. 그래서, state s에서 얻을 수 있는 가능한 좋은 미래 보상은 max_a'*Q(s',a')*로 정의될 예정입니다. (여기의 최대는 state *s'*에서 가능한 모든 a' 액션으로 계산합니다.)

주어진 a 액션에서, state s의 Q-Table 값을 계산하는 Bellman formula가 주어집니다:

여기 y는 미래 보상보다 현재 보상을 얼마나 선호하는지 판단하는 discount factor로 불리고 있고 반대의 경우도 그렇습니다.

알고리즘 학습

다음 방정식이 주어지면, 학습 알고리즘의 의사 코드를 작성할 수 있습니다:

모든 state와 액션에 대하여 같은 숫자로 Q-Table Q 초기화
학습률 α ← 1 설정
수차례 시뮬레이션 반복
1. 랜덤 위치에서 시작
2. 반복
  1. state s 에서 a 액션 선택
  2. 새로운 state s' 로 이동해서 액션 수행
  3. 게임이 끝나는 조건이 생기거나, 또는 총 보상이 너무 작은 경우 - 시뮬레이션 종료
  4. 새로운 state에서 r 보상 계산
  5. Bellman 방정식 따라서 Q-Function 업데이트 : Q(s,a) ← (1-α)Q(s,a)+α(r+γ max_a'Q(s',a'))
  6. s ← s'
  7. 총 보상을 업데이트하고 α. 감소

Exploit vs. explore

다음 알고리즘에서, 2.1 단계에 액션을 어떻게 선택하는지 명확하지 않습니다. 만약 랜덤으로 액션을 선택하면, 환경을 램덤으로 explore하게 되고, 일반적으로 가지 않는 영역도 탐험하게 되면서 꽤 자주 죽을 것 같습니다. 다른 방식은 이미 알고 있는 Q-Table 값을 exploit하고, state s에서 최고의 액션 (높은 Q-Table 값)을 선택하는 방식입니다. 그러나, 다른 state를 막을 수 있고, 최적의 솔루션을 찾지 못할 수 있습니다.

따라서, 최적의 방식은 exploration과 exploitation 사이 밸런스를 잘 조절하는 것입니다. 이는 Q-Table 값에 확률로 비례한 state s에서 액션을 선택할 수 있습니다. 초반에, Q-Table 값이 모두 같을 때, 랜덤 선택에 해당하겠지만, 환경을 더 배운다면, agent가 탐험하지 않은 경로를 선택하면서, 최적 경로를 따라갈 가능성이 커집니다.

Python 구현

지금 학습 알고리즘을 구현할 준비가 되었습니다. 그 전에, Q-Table에서 임의 숫자를 액션과 대응되는 확률 백터로 변환하는 일부 함수가 필요합니다.

probs() 함수를 만듭니다:
```
def probs(v,eps=1e-4):
    v = v-v.min()+eps
    v = v/v.sum()
    return v
```
백터의 모든 컴포넌트가 똑같다면, 초기 케이스에서 0으로 나누는 것을 피하기 위해서 원본 백터에 약간의 eps를 추가합니다.

epochs라고 불리는, 5000번 실험으로 학습 알고리즘을 실행합니다: (code block 8)

    for epoch in range(5000):
    
        # Pick initial point
        m.random_start()
        
        # Start travelling
        n=0
        cum_reward = 0
        while True:
            x,y = m.human
            v = probs(Q[x,y])
            a = random.choices(list(actions),weights=v)[0]
            dpos = actions[a]
            m.move(dpos,check_correctness=False) # we allow player to move outside the board, which terminates episode
            r = reward(m)
            cum_reward += r
            if r==end_reward or cum_reward < -1000:
                lpath.append(n)
                break
            alpha = np.exp(-n / 10e5)
            gamma = 0.5
            ai = action_idx[a]
            Q[x,y,ai] = (1 - alpha) * Q[x,y,ai] + alpha * (r + gamma * Q[x+dpos[0], y+dpos[1]].max())
            n+=1

이 알고리즘이 실행된 후, Q-Table은 각 단계에 다른 액션의 attractiveness를 정의하는 값으로 업데이트해야 합니다. 움직이고 싶은 방향의 방향으로 각 셀에 백터를 plot해서 Q-Table을 시각화할 수 있습니다. 단순하게, 화살표 머리 대신 작은 원을 그립니다.

정책 확인

Q-Table은 각 state에서 각 액션의 "attractiveness"를 리스트로 가지고 있으므로, 사용해서 세계에서 실력있는 네비게이션으로 정의하는 것은 상당히 쉽습니다. 간편한 케이스는, 가장 높은 Q-Table 값에 상응하는 액션을 선택할 수 있는 경우입니다: (code block 9)

def qpolicy_strict(m):
        x,y = m.human
        v = probs(Q[x,y])
        a = list(actions)[np.argmax(v)]
        return a

walk(m,qpolicy_strict)

만약 코드를 여러 번 시도하면, 가끔 "hangs"을 일으키고, 노트북에 있는 STOP 버튼을 눌러서 중단할 필요가 있다는 점을 알게 됩니다. 최적 Q-Value의 측면에서 두 state가 "point"하는 상황이 있을 수 있기 때문에, 이러한 케이스에는 agent가 그 state 사이를 무한으로 이동하는 현상이 발생됩니다.

🚀 도전

Task 1: 특정 걸음 (say, 100) 숫자로 경로의 최대 길이를 제한하는 walk 함수를 수정하고, 가끔 코드가 이 값을 반환하는지 지켜봅니다.

Task 2: 이미 이전에 갔던 곳으로 돌아가지 않도록 walk 함수를 수정합니다. walk를 반복하는 것을 막을 수 있지만, agent가 탈출할 수 없는 곳은 여전히 "trapped" 될 수 있습니다.

더 좋은 네비게이션 정책으로 exploitation과 exploration을 합쳐서, 훈련 중에 사용했습니다. 이 정책에서, Q-Table 값에 비례해서, 특정 확률로 각 액션을 선택할 예정입니다. 이 전략은 이미 탐험한 위치로 agent가 돌아가는 결과를 도출할 수 있지만, 해당 코드에서 볼 수 있는 것처럼, 원하는 위치로 가는 평균 경로가 매우 짧게 결과가 나옵니다. (print_statistics가 100번 시뮬레이션 돌렸다는 점을 기억합니다): (code block 10)

def qpolicy(m):
        x,y = m.human
        v = probs(Q[x,y])
        a = random.choices(list(actions),weights=v)[0]
        return a

print_statistics(qpolicy)

이 코드가 실행된 후, 3-6의 범위에서, 이전보다 매우 작은 평균 경로 길이를 얻어야 합니다.

학습 프로세스 조사

언급했던 것처럼, 학습 프로세스는 문제 공간의 구조에 대해 얻은 지식에 exploration과 exploration 사이 밸런스를 잘 맞춥니다. 학습 결과가 (agent가 목표로 가는 깗은 경로를 찾을 수 있게 도와주는 능력) 개선되었던 것을 볼 수 있지만, 학습 프로세스를 하는 동안에 평균 경로 길이가 어떻게 작동하는지 보는 것도 흥미롭습니다:

배운 내용을 오약하면 이렇습니다:

평균 경로의 길이 증가. 처음 여기에서 볼 수 있는 것은, 평균 경로 길이가 증가하는 것입니다. 아마도 환경에 대해 잘 모를 때, 물 또는 늑대, 나쁜 state에 걸릴 수 있다는 사실입니다. 더 배우고 지식으로 시작하면, 환경을 오래 탐험할 수 있지만, 여전히 사과가 어디에 자라고 있는지 잘 모릅니다.
배울수록, 경로 길이 감소. 충분히 배웠으면, agent가 목표를 달성하는 것은 더 쉽고, 경로 길이가 줄어들기 시작합니다. 그러나 여전히 탐색하게 되므로, 최적의 경로를 자주 빗겨나가고, 새로운 옵션을 탐험해서, 경로를 최적 경로보다 길게 만듭니다.
급격한 길이 증가. 이 그래프에서 관찰할 수 있는 약간의 포인트는, 갑자기 길이가 길어졌다는 것입니다. 프로세스의 추계학 특성을 나타내고, 일부 포인트에서 새로운 값을 덮어쓰는 Q-Table 계수로 "spoil"될 수 있습니다. 관성적으로 학습률을 줄여서 최소화해야 합니다 (예시로, 훈련이 끝나기 직전에, 작은 값으로만 Q-Table 값을 맞춥니다).

전체적으로, 학습 프로세스의 성공과 퀄리티는 학습률, 학습률 감소, 그리고 감가율처럼 파라미터에 기반하는게 상당히 중요하다는 점을 기억합니다. 훈련하면서 최적화하면 (예시로, Q-Table coefficients), parameters와 구별해서, 가끔 hyperparameters라고 불립니다. 최고의 hyperparameter 값을 찾는 프로세스는 hyperparameter optimization이라고 불리며, 별도의 토픽이 있을 만합니다.

강의 후 퀴즈

과제

A More Realistic World

19 KiB Raw Blame History Unescape Escape