|
|
2 years ago | |
|---|---|---|
| .. | ||
| README.it.md | 2 years ago | |
| README.ko.md | 2 years ago | |
| README.zh-cn.md | 2 years ago | |
| assignment.es.md | ||
| assignment.it.md | ||
| assignment.ko.md | ||
| assignment.zh-cn.md | ||
README.zh-cn.md
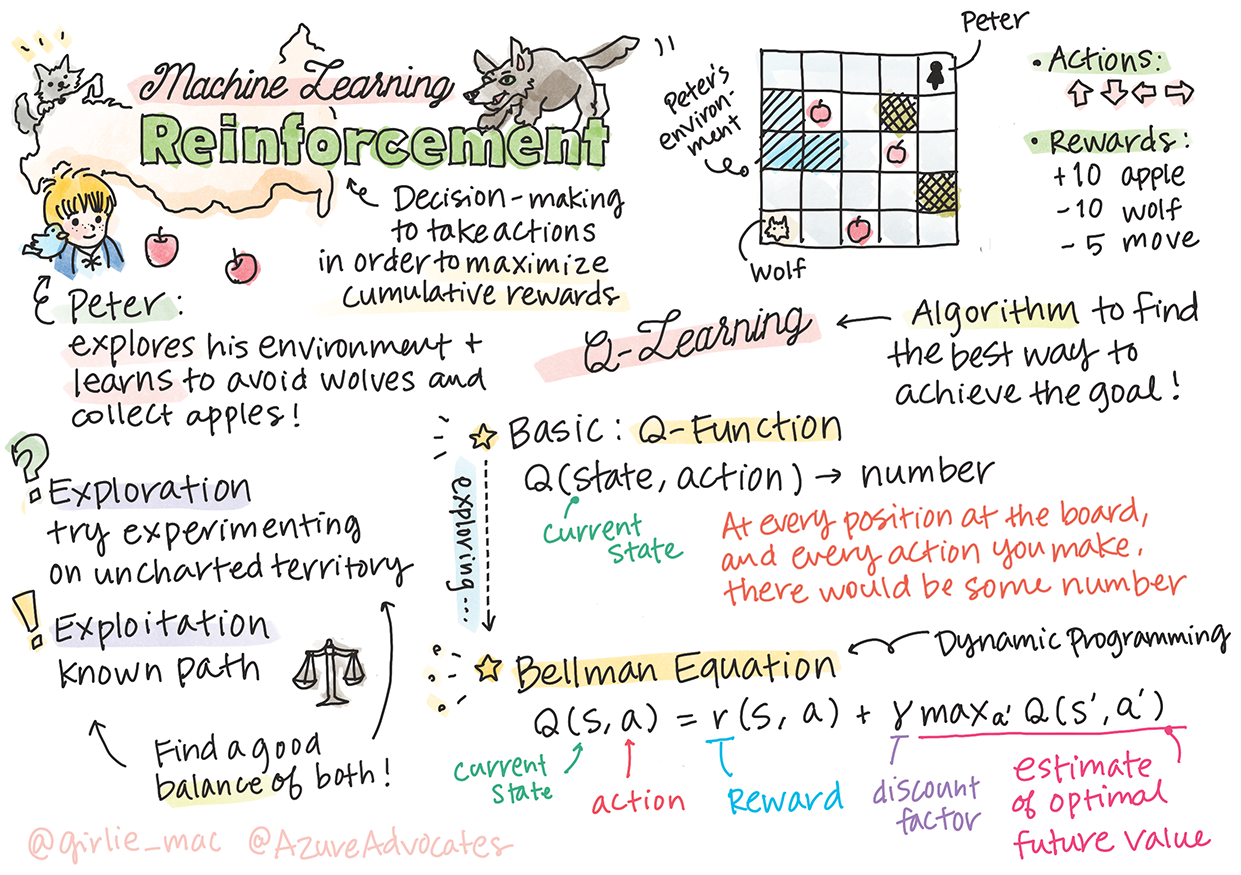
强化学习和 Q-Learning 介绍
作者 Tomomi Imura
强化学习涉及三个重要概念:代理、一些状态和每个状态的一组动作。通过在指定状态下执行一个动作,代理会得到奖励。想象一下电脑游戏超级马里奥。你是马里奥,你在一个游戏关卡中,站在悬崖边上。在你上面是一枚硬币。你是马里奥,在游戏关卡里,在特定位置......这就是你的状态。向右移动一步(一个动作)会让跌下悬崖,而且会得到一个低分。然而,按下跳跃按钮会让你活下来并得分。这是一个积极的结果,它会给你一个积极、正向的分数。
通过使用强化学习和模拟器(游戏),你可以学习如何玩游戏以最大化奖励,既能够活下去还可以获得尽可能多的积分。
🎥 点击上图观看 Dmitry 讨论强化学习
课前测验
先决条件和设置
在本课中,我们将用 Python 代码做一些试验。你应该能够在你的计算机上或云中的某个地方运行本课程中的 Jupyter Notebook 代码。
你可以打开课本笔记本 并通过学习本课进行编译、运行。
注意: 如果你是从云端打开此代码,你还需要获取笔记本代码中使用的
rlboard.py文件。将其添加到与笔记本相同的目录中。
介绍
在本课中,我们将探索 彼得与狼 的世界,其灵感来自俄罗斯作曲家 Sergei Prokofiev的音乐童话。我们将使用强化学习让彼得探索他的环境,收集美味的苹果并避免遇到狼。
强化学习(RL)是一种学习技术,它允许我们通过运行许多实验来学习代理在某些环境中的最佳行为。这种环境中的代理应该有一些目标,由奖励函数定义。
环境
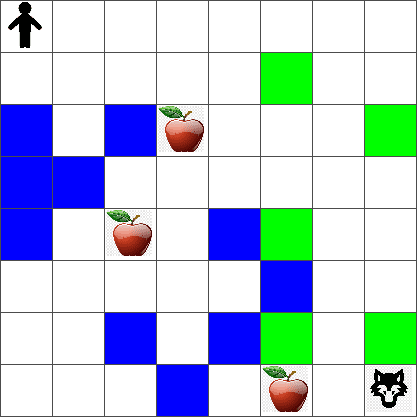
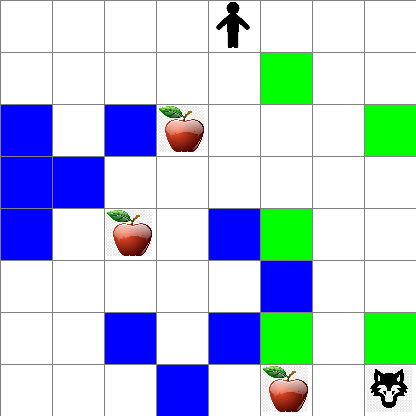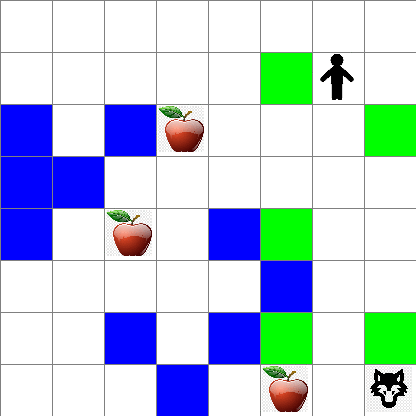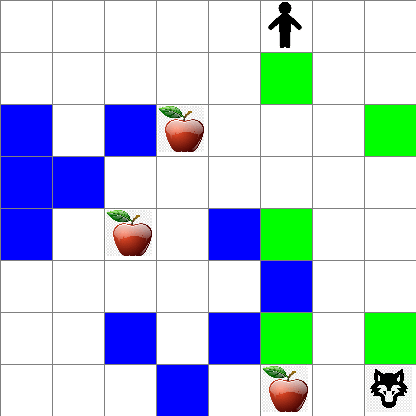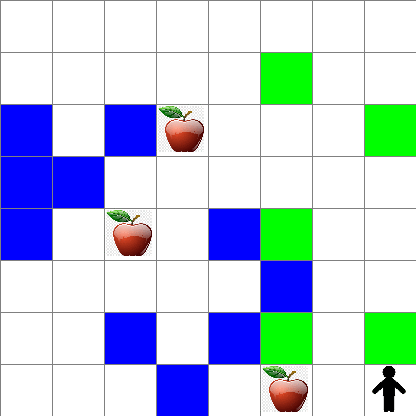
为简单起见,让我们将 Peter 的世界视为一个大小为 width x height 的方板,如下所示:
该板中的每个单元格可以是:
- 地面,彼得和其他生物可以在上面行走。
- 水,不能在上面行走。
- 树或草,可以休息的地方。
- 苹果,代表彼得希望找到用来喂饱自己的食物。
- 狼,这是危险的,应该避免遇到。
有一个单独的 Python 模块 rlboard.py,其中包含在此环境中工作的代码。因为这段代码对于理解我们的概念并不重要,我们将导入该模块并使用它来创建示例板(代码块 1):
from rlboard import *
width, height = 8,8
m = Board(width,height)
m.randomize(seed=13)
m.plot()
这段代码会打印一张类似于上面的环境图片。
行动和策略
在我们的例子中,彼得的目标是找到苹果,同时避开狼和其他障碍物。为此,他可以四处走动,直到找到一个苹果。
因此,在任何位置,他都可以选择以下动作之一:向上、向下、向左和向右。
我们将这些动作定义为字典,并将它们映射到相应的坐标变化对。例如,向右移动 (R) 将对应于一对 (1,0)。(代码块 2):
actions = { "U" : (0,-1), "D" : (0,1), "L" : (-1,0), "R" : (1,0) }
action_idx = { a : i for i,a in enumerate(actions.keys()) }
综上所述,本场景的策略和目标如下:
-
我们的代理(彼得)的策略由一个函数定义,它返回任何给定状态下的动作。在我们的例子中,问题的状态由棋盘表示,包括玩家的当前位置。
-
目标,强化学习的目的是学习一个好的策略,使我们能够有效地解决问题。但是,作为基准,让我们考虑称为 随机走动 的最简单策略。
随机走动
让我们首先通过实施随机走动策略来解决我们的问题。通过随机走动,我们从允许的动作中随机选择下一个动作,直到我们找到苹果(代码块 3)。
-
使用以下代码实现随机走动:
def random_policy(m): return random.choice(list(actions)) def walk(m,policy,start_position=None): n = 0 # number of steps # set initial position if start_position: m.human = start_position else: m.random_start() while True: if m.at() == Board.Cell.apple: return n # success! if m.at() in [Board.Cell.wolf, Board.Cell.water]: return -1 # eaten by wolf or drowned while True: a = actions[policy(m)] new_pos = m.move_pos(m.human,a) if m.is_valid(new_pos) and m.at(new_pos)!=Board.Cell.water: m.move(a) # do the actual move break n+=1 walk(m,random_policy)对
walk的调用应返回相应路径的长度,该长度可能因每次运行而不同。 -
多次运行该实验(例如 100 次),并打印结果统计信息(代码块 4):
def print_statistics(policy): s,w,n = 0,0,0 for _ in range(100): z = walk(m,policy) if z<0: w+=1 else: s += z n += 1 print(f"Average path length = {s/n}, eaten by wolf: {w} times") print_statistics(random_policy)请注意,一条路径的平均长度约为 30-40 步,考虑到到最近苹果的平均距离约为 5-6 步,这一数字相当大。
你还可以看到 Peter 在随机走动过程中的运动情况:
奖励函数
为了使我们的策略更加智能,我们需要了解哪些动作比其他动作 "更好"。为此,我们需要定义我们的目标。
可以根据奖励函数来定义目标,该函数将为每个状态返回一些分数值。数字越大,奖励函数越好。(代码块 5)
move_reward = -0.1
goal_reward = 10
end_reward = -10
def reward(m,pos=None):
pos = pos 或 m.human
if not m.is_valid(pos):
return end_reward
x = m.at(pos)
if x==Board.Cell.water or x == Board.Cell.wolf:
return end_reward
if x==Board.Cell.apple:
return goal_reward
return move_reward
关于奖励函数的一个有趣的事情是,在大多数情况下,我们只在游戏结束时才得到实质性的奖励。这意味着我们的算法应该以某种方式记住最终导致积极奖励的"好"步骤,并增加它们的重要性。同样,所有导致不良结果的举动都应该被阻拦。
Q-Learning
我们将在这里讨论的一种叫做 Q-Learning 的算法。在该算法中,策略由称为 Q-Table 的函数(或数据结构)定义。它记录了给定状态下每个动作的"优点"。
之所以称为 Q-Table,是因为表格或多维数组通常表示起来很方便。由于我们的棋盘尺寸为 "width"x"height",我们可以使用形状为 "width"x"height"x"len(actions) 的 numpy 数组来表示 Q-Table:(代码块6)
Q = np.ones((width,height,len(actions)),dtype=np.float)*1.0/len(actions)
请注意,我们将 Q-Table 的所有值初始化为一个相等的值,在我们的例子中为 "-0.25"。这对应于"随机走动"策略,因为每个状态中的所有移动都同样好。我们可以将 Q-Table 传递给 plot 函数,以便在板上可视化表格:m.plot(Q)。
在每个单元格的中心有一个"箭头",表示首选的移动方向。由于所有方向都相等,因此显示一个点。
现在我们需要运行这个程序,探索我们的环境,并学习更好的 Q-Table 值分布,这将使我们能够更快地找到通往苹果的路径。
Q-Learning 的本质:贝尔曼方程
一旦我们开始移动,每个动作都会有相应的奖励,即理论上我们可以根据最高的即时奖励来选择下一个动作。但是,在大多数情况,此举不会实现我们到达苹果的目标,因此我们无法立即决定哪个方向更好。
请记住,重要的不是直接结果,而是我们将在模拟结束时获得的最终结果。
为了解释这种延迟奖励,我们需要使用**动态规划** 的原则,它允许我们递归地思考问题。
假设我们现在处于状态 s,并且我们想要移动到下一个状态 s'。通过这样做,我们将收到由奖励函数定义的即时奖励 r(s,a),以及一些未来的奖励。如果我们假设我们的 Q-Table 正确反映了每个动作的“吸引力”,那么在状态 s' 我们将选择对应于 Q(s',a') 最大值的动作 a。因此,我们可以在状态 s 获得的最佳未来奖励将被定义为 maxa'Q(s',a')(这里的最大值是在状态 s' 时所有可能的动作 a' 上计算的)。
这给出了 Bellman 公式,用于计算状态 s 的 Q-Table 值,给定动作 a:

这里 γ 是所谓的折扣因子,它决定了你应该在多大程度上更喜欢当前的奖励而不是未来的奖励,反之亦然。
学习算法
鉴于上面的等式,我们现在可以为我们的学习算法编写伪代码:
- 用相同的数字为所有状态和动作初始化 Q-Table Q
- 设置学习率α ← 1
- 多次重复模拟
- 随机位置开始
- 重复
- 在状态 s 选择一个动作 a 2.通过移动到新状态 s' 来执行动作 3.如果我们遇到游戏结束的情况,或者总奖励太少——退出模拟
- 计算新状态下的奖励 r
- 根据 Bellman 方程更新 Q-Function: Q(s,a) ← (1-α)Q(s,a)+α(r+γ maxa'Q( s',a'))
- s ← s'
- 更新总奖励并减少 α。
利用与探索
在上面的算法中,我们没有指定在步骤 2.1 中我们应该如何选择一个动作。如果我们随机选择动作,我们会随机探索环境,我们很可能会经常死亡以及探索我们通常不会去的区域。另一种方法是利用我们已经知道的 Q-Table 值,从而在状态 s 选择最佳动作(具有更高的 Q-Table 值)。然而,这将阻止我们探索其他状态,而且我们可能找不到最佳解决方案。
因此,最好的方法是在探索和开发之间取得平衡。这可以通过选择状态 s 的动作来完成,概率与 Q 表中的值成正比。一开始,当 Q-Table 值都相同时,它将对应于随机选择,但是随着我们对环境的了解越来越多,我们将更有可能遵循最佳路线,同时允许智能体偶尔选择未探索的路径。
Python 实现
我们现在准备实现学习算法。在我们这样做之前,我们还需要一些函数来将 Q-Table 中的任意数字转换为相应动作的概率向量。
-
创建一个函数
probs():def probs(v,eps=1e-4): v = vv.min()+eps v = v/v.sum() return v我们向原始向量添加了一些
eps,以避免在初始情况下被 0 除,此时向量的所有分量都相同。
通过 5000 次实验运行他们的学习算法,也称为 epochs:(代码块 8)
for epoch in range(5000):
# Pick initial point
m.random_start()
# Start travelling
n=0
cum_reward = 0
while True:
x,y = m.human
v = probs(Q[x,y])
a = random.choices(list(actions),weights=v)[0]
dpos = actions[a]
m.move(dpos,check_correctness=False) # we allow player to move outside the board, which terminates episode
r = reward(m)
cum_reward += r
if r==end_reward or cum_reward < -1000:
lpath.append(n)
break
alpha = np.exp(-n / 10e5)
gamma = 0.5
ai = action_idx[a]
Q[x,y,ai] = (1 - alpha) * Q[x,y,ai] + alpha * (r + gamma * Q[x+dpos[0], y+dpos[1]].max())
n+=1
执行此算法后,应使用定义每个步骤不同动作的吸引力的值更新 Q-Table 。我们可以尝试通过在每个单元格上绘制一个向量来可视化 Q-Table,该向量将指向所需的移动方向。为简单起见,我们画一个小圆圈而不是箭头。

检查策略
由于 Q-Table 列出了每个状态下每个动作的"吸引力",因此很容易使用它来定义我们世界中的高效导航。在最简单的情况下,我们可以选择最高 Q-Table 值对应的 action:(代码块9)
def qpolicy_strict(m):
x,y = m.human
v = probs(Q[x,y])
a = list(actions)[np.argmax(v)]
return a
walk(m,qpolicy_strict)
如果你多次尝试上面的代码,你可能会注意到它有时会"挂起",你需要按笔记本中的 STOP 按钮来中断它。发生这种情况是因为可能存在两种状态在最佳 Q 值方面"指向"彼此的情况,在这种情况下,代理最终会在这些状态之间无限期地移动。
🚀挑战
任务 1: 修改
walk函数,将路径的最大长度限制为一定的步数(比如 100),并时不时地观察上面的代码返回值。
任务 2: 修改
walk函数,使其不会回到之前已经去过的地方。这将防止walk循环,但是,代理仍然可能最终"被困"在它无法逃脱的位置。
导航
更好的导航策略是我们在训练期间使用的,它结合了利用和探索。在这个策略中,我们将以一定的概率选择每个动作,与 Q-Table 中的值成比例。这种策略可能仍会导致代理返回到它已经探索过的位置,但是,正如你从下面的代码中看到的,它会导致到达所需位置的平均路径非常短(请记住,print_statistics 运行模拟100次):(代码块10)
def qpolicy(m):
x,y = m.human
v = probs(Q[x,y])
a = random.choices(list(actions),weights=v)[0]
return a
print_statistics(qpolicy)
运行此代码后,你应该获得比以前小得多的平均路径长度,范围为 3-6。
调查学习过程
正如我们已经提到的,学习过程是探索和探索有关问题空间结构的知识之间的平衡。我们已经看到学习的结果(帮助代理找到到达目标的短路径的能力)有所改善,但观察平均路径长度在学习过程中的表现也很有趣:

学习内容可以概括为:
-
平均路径长度增加。我们在这里看到的是,起初,平均路径长度增加。这可能是因为当我们对环境一无所知时,我们很可能会陷入糟糕的状态,水或狼。随着我们学习更多并开始使用这些知识,我们可以更长时间地探索环境,但我们仍然不知道苹果在哪里。
-
随着我们了解更多,路径长度减少。一旦我们学习得足够多,代理就更容易实现目标,路径长度开始减少。然而,我们仍然对探索持开放态度,因此我们经常偏离最佳路径,并探索新的选择,使路径比最佳路径更长。
-
长度突然增加。我们在这张图上还观察到,在某个时刻,长度突然增加。这表明该过程的随机性,我们可以在某个时候通过用新值覆盖 Q-Table 系数来"破坏" Q-Table 系数。理想情况下,这应该通过降低学习率来最小化(例如,在训练结束时,我们只调整 Q-Table 很小的一个小值)。
总的来说,重要的是要记住学习过程的成功和质量在很大程度上取决于参数,例如学习率、学习率衰减和折扣因子。这些通常称为超参数,以区别于我们在训练期间优化的参数(例如,Q-Table 系数)。寻找最佳超参数值的过程称为超参数优化,它值得一个单独的话题来介绍。