13 KiB

Raw Permalink Blame History

시계열 예측 소개

스케치노트 제공: Tomomi Imura

이번 강의와 다음 강의에서는 시계열 예측에 대해 배워볼 것입니다. 시계열 예측은 머신러닝 과학자의 도구 중에서 흥미롭고 가치 있는 부분으로, 다른 주제들에 비해 덜 알려져 있습니다. 시계열 예측은 일종의 '수정 구슬'과 같아서, 가격과 같은 변수의 과거 성과를 기반으로 미래의 잠재적 가치를 예측할 수 있습니다.

🎥 위 이미지를 클릭하면 시계열 예측에 대한 동영상을 볼 수 있습니다.

강의 전 퀴즈

시계열 예측은 가격 책정, 재고 관리, 공급망 문제와 같은 비즈니스 문제에 직접적으로 적용될 수 있어 실질적인 가치를 지닌 흥미로운 분야입니다. 딥러닝 기술이 미래 성과를 더 잘 예측하기 위해 더 많은 통찰력을 제공하기 시작했지만, 시계열 예측은 여전히 고전적인 머신러닝 기술에 의해 크게 영향을 받는 분야입니다.

펜실베니아 주립대의 유용한 시계열 커리큘럼은 여기에서 확인할 수 있습니다.

소개

스마트 주차 미터 배열을 관리한다고 가정해봅시다. 이 미터는 시간이 지남에 따라 얼마나 자주 사용되었는지, 얼마나 오래 사용되었는지에 대한 데이터를 제공합니다.

미터의 과거 성과를 기반으로 공급과 수요의 법칙에 따라 미래 가치를 예측할 수 있다면 어떨까요?

목표를 달성하기 위해 언제 행동해야 할지 정확히 예측하는 것은 시계열 예측으로 해결할 수 있는 도전 과제입니다. 사람들이 주차 공간을 찾는 바쁜 시간에 더 많은 요금을 부과하는 것은 기분 좋지 않을 수 있지만, 거리를 청소하기 위한 수익을 창출하는 확실한 방법이 될 것입니다!

이제 시계열 알고리즘의 유형을 탐구하고 데이터를 정리하고 준비하기 위한 노트북을 시작해봅시다. 여러분이 분석할 데이터는 GEFCom2014 예측 대회에서 가져온 것으로, 2012년부터 2014년까지 3년간의 시간별 전력 사용량과 온도 값을 포함하고 있습니다. 전력 사용량과 온도의 과거 패턴을 바탕으로 전력 사용량의 미래 값을 예측할 수 있습니다.

이 예제에서는 과거 사용량 데이터만을 사용하여 한 시간 단위로 예측하는 방법을 배울 것입니다. 그러나 시작하기 전에, 이 과정에서 어떤 일이 일어나는지 이해하는 것이 유용합니다.

몇 가지 정의

'시계열'이라는 용어를 접할 때, 여러 다른 맥락에서의 사용을 이해해야 합니다.

🎓 시계열

수학에서 "시계열은 시간 순서로 나열되거나 그래프로 표시된 데이터 포인트의 시리즈입니다. 가장 일반적으로 시계열은 일정한 간격으로 연속적으로 측정된 데이터의 시퀀스입니다." 시계열의 예로는 다우존스 산업평균지수의 일일 종가가 있습니다. 시계열 플롯과 통계 모델링은 신호 처리, 날씨 예측, 지진 예측, 그리고 시간이 지나면서 데이터를 플롯할 수 있는 다른 분야에서 자주 사용됩니다.

🎓 시계열 분석

시계열 분석은 위에서 언급한 시계열 데이터를 분석하는 것입니다. 시계열 데이터는 '중단된 시계열'과 같이 중단 이벤트 전후의 시계열 진화 패턴을 감지하는 것을 포함하여 다양한 형태를 취할 수 있습니다. 시계열에 필요한 분석 유형은 데이터의 특성에 따라 다릅니다. 시계열 데이터 자체는 숫자 또는 문자 시리즈 형태를 취할 수 있습니다.

분석은 주파수 영역, 시간 영역, 선형 및 비선형 등 다양한 방법을 사용합니다. 이 유형의 데이터를 분석하는 다양한 방법에 대해 더 알아보기.

🎓 시계열 예측

시계열 예측은 과거에 수집된 데이터가 보여주는 패턴을 기반으로 미래 값을 예측하기 위해 모델을 사용하는 것입니다. 시계열 데이터를 탐색하기 위해 회귀 모델을 사용하는 것이 가능하지만, 시간 지수를 플롯의 x 변수로 사용하는 경우, 이러한 데이터는 특별한 유형의 모델을 사용하는 것이 가장 좋습니다.

시계열 데이터는 선형 회귀로 분석할 수 있는 데이터와 달리 순서가 있는 관측값 목록입니다. 가장 일반적인 모델은 ARIMA로, "자기회귀 통합 이동평균"을 의미합니다.

ARIMA 모델은 "시리즈의 현재 값을 과거 값과 과거 예측 오류와 관련짓습니다." 이러한 모델은 시간 순서로 정렬된 데이터를 분석하는 데 가장 적합합니다.

ARIMA 모델에는 여러 유형이 있으며, 여기에서 배울 수 있으며 다음 강의에서 다룰 것입니다.

다음 강의에서는 단변량 시계열을 사용하여 ARIMA 모델을 구축할 것입니다. 단변량 시계열은 시간이 지남에 따라 값이 변하는 하나의 변수에 초점을 맞춥니다. 이러한 유형의 데이터의 예로는 Mauna Loa Observatory에서 월별 CO2 농도를 기록한 이 데이터셋이 있습니다:

CO2	YearMonth	Year	Month
330.62	1975.04	1975	1
331.40	1975.13	1975	2
331.87	1975.21	1975	3
333.18	1975.29	1975	4
333.92	1975.38	1975	5
333.43	1975.46	1975	6
331.85	1975.54	1975	7
330.01	1975.63	1975	8
328.51	1975.71	1975	9
328.41	1975.79	1975	10
329.25	1975.88	1975	11
330.97	1975.96	1975	12

✅ 이 데이터셋에서 시간이 지남에 따라 변하는 변수를 식별하세요.

시계열 데이터의 특성 고려하기

시계열 데이터를 살펴보면, 특정 특성을 가지고 있다는 것을 알 수 있습니다. 이러한 특성을 고려하고 완화하여 데이터의 패턴을 더 잘 이해할 수 있습니다. 시계열 데이터를 분석하려는 '신호'로 간주한다면, 이러한 특성은 '노이즈'로 생각할 수 있습니다. 통계적 기법을 사용하여 이러한 '노이즈'를 줄여야 할 때가 많습니다.

다음은 시계열 데이터를 다루기 위해 알아야 할 몇 가지 개념입니다:

🎓 추세

추세는 시간에 따라 측정 가능한 증가와 감소로 정의됩니다. 더 알아보기. 시계열의 맥락에서 추세를 사용하는 방법과 필요하다면 추세를 제거하는 방법에 대해 알아보세요.

🎓 계절성

계절성은 주기적인 변동으로 정의됩니다. 예를 들어, 휴일 시즌의 판매량 증가가 이에 해당합니다. 여기에서 계절성을 데이터에서 표시하는 다양한 플롯 유형을 확인하세요.

🎓 이상치

이상치는 표준 데이터 변동에서 멀리 떨어져 있는 값입니다.

🎓 장기 주기

계절성과는 별개로, 데이터는 1년 이상 지속되는 경제 침체와 같은 장기 주기를 나타낼 수 있습니다.

🎓 일정한 분산

시간이 지나면서 일부 데이터는 일정한 변동을 나타냅니다. 예를 들어, 낮과 밤의 에너지 사용량.

🎓 급격한 변화

데이터는 추가 분석이 필요한 급격한 변화를 나타낼 수 있습니다. 예를 들어, COVID로 인해 사업체가 갑작스럽게 문을 닫으면서 데이터에 변화가 생겼습니다.

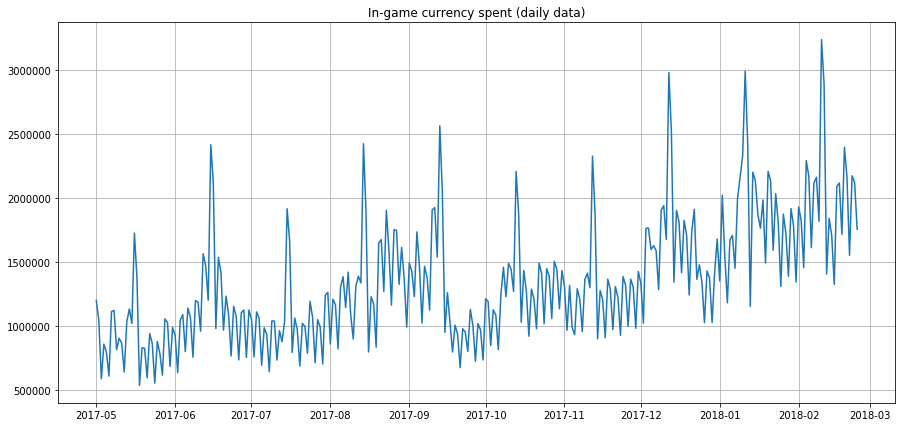
✅ 샘플 시계열 플롯을 확인하세요. 몇 년 동안의 일일 게임 내 통화 사용량을 보여줍니다. 위에서 나열된 특성 중 어떤 것을 이 데이터에서 식별할 수 있나요?

연습 - 전력 사용량 데이터 시작하기

이제 과거 사용량을 기반으로 미래 전력 사용량을 예측하는 시계열 모델을 만들어 봅시다.

이 예제의 데이터는 GEFCom2014 예측 대회에서 가져온 것입니다. 2012년부터 2014년까지 3년간의 시간별 전력 사용량과 온도 값을 포함하고 있습니다.

Tao Hong, Pierre Pinson, Shu Fan, Hamidreza Zareipour, Alberto Troccoli and Rob J. Hyndman, "Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond", International Journal of Forecasting, vol.32, no.3, pp 896-913, July-September, 2016.

이 강의의 working 폴더에서 notebook.ipynb 파일을 엽니다. 데이터를 로드하고 시각화하는 데 도움이 되는 라이브러리를 추가하세요.
```
import os
import matplotlib.pyplot as plt
from common.utils import load_data
%matplotlib inline
```
참고로, 포함된 common 폴더의 파일을 사용하여 환경을 설정하고 데이터를 다운로드합니다.
다음으로, load_data()와 head()를 호출하여 데이터프레임으로 데이터를 확인하세요:
```
data_dir = './data'
energy = load_data(data_dir)[['load']]
energy.head()
```
두 개의 열이 날짜와 사용량을 나타내는 것을 볼 수 있습니다:

load

2012-01-01 00:00:00 2698.0

2012-01-01 01:00:00 2558.0

2012-01-01 02:00:00 2444.0

2012-01-01 03:00:00 2402.0

2012-01-01 04:00:00 2403.0

	load
2012-01-01 00:00:00	2698.0
2012-01-01 01:00:00	2558.0
2012-01-01 02:00:00	2444.0
2012-01-01 03:00:00	2402.0
2012-01-01 04:00:00	2403.0

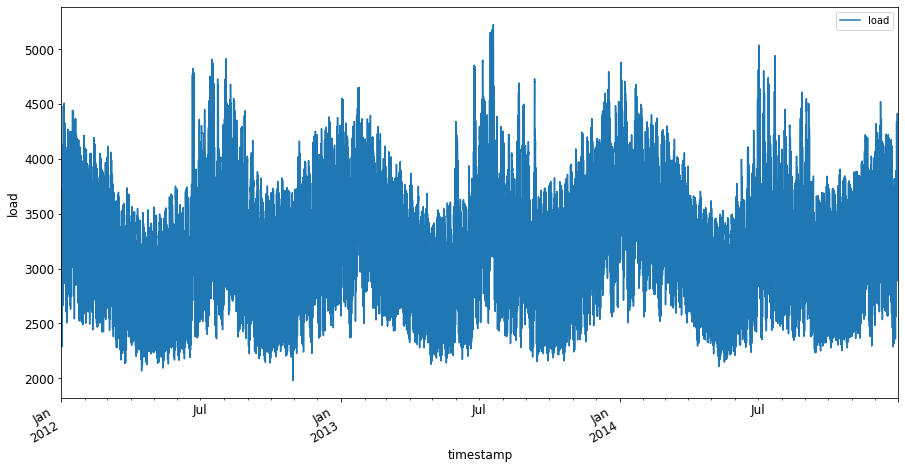
이제 plot()을 호출하여 데이터를 플롯하세요:

energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

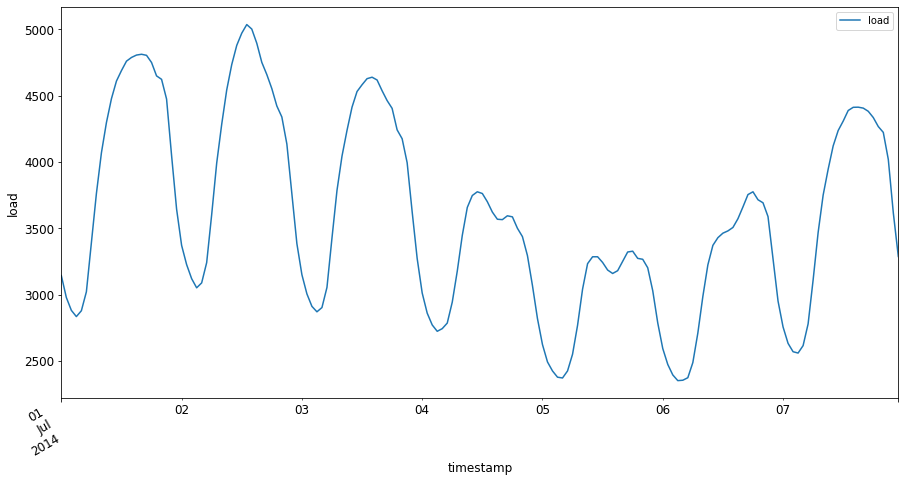
이제 2014년 7월 첫째 주를 [시작 날짜]:[종료 날짜] 패턴으로 energy에 입력하여 플롯하세요:
```
energy['2014-07-01':'2014-07-07'].plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
멋진 플롯입니다! 이러한 플롯을 살펴보고 위에서 나열된 특성 중 어떤 것을 확인할 수 있는지 살펴보세요. 데이터를 시각화함으로써 무엇을 추론할 수 있을까요?

다음 강의에서는 ARIMA 모델을 만들어 예측을 생성할 것입니다.

🚀도전 과제

시계열 예측이 도움이 될 수 있는 모든 산업 및 연구 분야를 목록으로 만들어 보세요. 예술, 계량경제학, 생태학, 소매업, 산업, 금융 등에서 이러한 기술의 응용 사례를 생각해볼 수 있나요? 또 다른 분야는 어디일까요?

강의 후 퀴즈

복습 및 자기 학습

여기서는 다루지 않지만, 신경망은 때때로 고전적인 시계열 예측 방법을 강화하는 데 사용됩니다. 이에 대해 이 기사를 읽어보세요.

과제

더 많은 시계열 시각화하기

면책 조항:
이 문서는 AI 번역 서비스 Co-op Translator를 사용하여 번역되었습니다. 정확성을 위해 최선을 다하고 있으나, 자동 번역에는 오류나 부정확성이 포함될 수 있습니다. 원본 문서를 해당 언어로 작성된 상태에서 권위 있는 자료로 간주해야 합니다. 중요한 정보의 경우, 전문적인 인간 번역을 권장합니다. 이 번역 사용으로 인해 발생하는 오해나 잘못된 해석에 대해 당사는 책임을 지지 않습니다.

13 KiB Raw Permalink Blame History