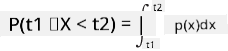24 KiB

Raw Permalink Blame History Unescape Escape

Utangulizi Mfupi wa Takwimu na Uwezekano


Takwimu na Uwezekano - Sketchnote na @nitya

Nadharia ya Takwimu na Uwezekano ni maeneo mawili yanayohusiana sana ya Hisabati ambayo ni muhimu sana kwa Sayansi ya Data. Inawezekana kufanya kazi na data bila uelewa wa kina wa hisabati, lakini ni bora kujua angalau dhana za msingi. Hapa tutatoa utangulizi mfupi ambao utakusaidia kuanza.

Jaribio la Kabla ya Somo

Uwezekano na Mabadiliko ya Kawaida

Uwezekano ni namba kati ya 0 na 1 inayoonyesha uwezekano wa tukio fulani kutokea. Inafafanuliwa kama idadi ya matokeo chanya (yanayopelekea tukio hilo), ikigawanywa na jumla ya matokeo, kwa sharti kwamba matokeo yote yana uwezekano sawa. Kwa mfano, tunapopiga kete, uwezekano wa kupata namba shufwa ni 3/6 = 0.5.

Tunapozungumzia matukio, tunatumia mabadiliko ya kawaida. Kwa mfano, mabadiliko ya kawaida yanayowakilisha namba inayopatikana tunapopiga kete yatakuwa na thamani kati ya 1 hadi 6. Seti ya namba kutoka 1 hadi 6 inaitwa nafasi ya sampuli. Tunaweza kuzungumzia uwezekano wa mabadiliko ya kawaida kuchukua thamani fulani, kwa mfano P(X=3)=1/6.

Mabadiliko ya kawaida katika mfano uliopita yanaitwa ya kidhahiri, kwa sababu yana nafasi ya sampuli inayohesabika, yaani kuna thamani tofauti zinazoweza kuorodheshwa. Kuna matukio ambapo nafasi ya sampuli ni safu ya namba halisi, au seti nzima ya namba halisi. Mabadiliko kama hayo yanaitwa endelevu. Mfano mzuri ni muda wa kuwasili kwa basi.

Usambazaji wa Uwezekano

Kwa mabadiliko ya kawaida ya kidhahiri, ni rahisi kuelezea uwezekano wa kila tukio kwa kutumia kazi P(X). Kwa kila thamani s kutoka nafasi ya sampuli S, itatoa namba kati ya 0 na 1, ambapo jumla ya thamani zote za P(X=s) kwa matukio yote itakuwa 1.

Usambazaji wa kidhahiri unaojulikana zaidi ni usambazaji wa sare, ambapo kuna nafasi ya sampuli ya vipengele N, na uwezekano sawa wa 1/N kwa kila kimoja.

Ni vigumu zaidi kuelezea usambazaji wa uwezekano wa mabadiliko endelevu, yenye thamani zinazotolewa kutoka kwenye kipengele [a,b], au seti nzima ya namba halisi ℝ. Fikiria tukio la muda wa kuwasili kwa basi. Kwa kweli, kwa kila muda halisi wa kuwasili t, uwezekano wa basi kufika hasa wakati huo ni 0!

Sasa unajua kwamba matukio yenye uwezekano wa 0 hutokea, na mara nyingi sana! Angalau kila wakati basi linapofika!

Tunaweza tu kuzungumzia uwezekano wa mabadiliko kuangukia katika kipengele fulani cha thamani, kwa mfano P(t₁≤X<t₂). Katika kesi hii, usambazaji wa uwezekano unaelezewa na kazi ya msongamano wa uwezekano p(x), ambapo

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Mfano wa usambazaji wa sare endelevu unaitwa sare endelevu, ambao hufafanuliwa kwenye kipengele kilichofungwa. Uwezekano kwamba thamani X itaangukia kwenye kipengele cha urefu l ni sawia na l, na huongezeka hadi 1.

Usambazaji mwingine muhimu ni usambazaji wa kawaida, ambao tutazungumzia kwa undani zaidi hapa chini.

Wastani, Tofauti na Mkengeuko wa Kawaida

Tuseme tunachora mfuatano wa sampuli n za mabadiliko ya kawaida X: x₁, x₂, ..., x_n. Tunaweza kufafanua wastani (au wastani wa hesabu) wa mfuatano kwa njia ya kawaida kama (x₁+x₂+x_n)/n. Tunapoongeza ukubwa wa sampuli (yaani tunachukua kikomo n→∞), tutapata wastani (pia huitwa matarajio) wa usambazaji. Tutawakilisha matarajio kwa E(x).

Inaweza kuonyeshwa kwamba kwa usambazaji wowote wa kidhahiri wenye thamani {x₁, x₂, ..., x_N} na uwezekano unaolingana p₁, p₂, ..., p_N, matarajio yatakuwa sawa na E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Ili kutambua jinsi thamani zilivyo mbali, tunaweza kuhesabu tofauti σ² = ∑(x_i - μ)²/n, ambapo μ ni wastani wa mfuatano. Thamani σ inaitwa mkengeuko wa kawaida, na σ² inaitwa tofauti.

Hali, Median na Robo

Wakati mwingine, wastani hauwakilishi vyema thamani "ya kawaida" kwa data. Kwa mfano, wakati kuna thamani chache za juu sana ambazo ziko nje kabisa ya kiwango, zinaweza kuathiri wastani. Kiashiria kingine kizuri ni median, thamani ambayo nusu ya data iko chini yake, na nusu nyingine - juu yake.

Ili kutusaidia kuelewa usambazaji wa data, ni muhimu kuzungumzia robo:

Robo ya kwanza, au Q1, ni thamani ambayo 25% ya data iko chini yake
Robo ya tatu, au Q3, ni thamani ambayo 75% ya data iko chini yake

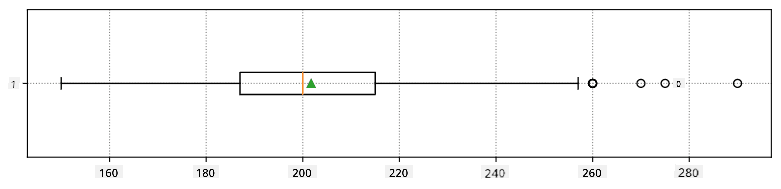
Kigrafu tunaweza kuwakilisha uhusiano kati ya median na robo katika mchoro unaoitwa box plot:

Hapa pia tunahesabu nafasi ya kati ya robo IQR=Q3-Q1, na kinachoitwa outliers - thamani ambazo ziko nje ya mipaka [Q1-1.5IQR,Q3+1.5IQR].

Kwa usambazaji wa kidhahiri unaojumuisha idadi ndogo ya thamani zinazowezekana, thamani "ya kawaida" nzuri ni ile inayojitokeza mara nyingi zaidi, ambayo inaitwa hali. Mara nyingi hutumika kwa data ya kategoria, kama vile rangi. Fikiria hali ambapo tuna vikundi viwili vya watu - baadhi wanapendelea sana nyekundu, na wengine wanapendelea bluu. Tukiwakilisha rangi kwa namba, wastani wa rangi inayopendwa ungekuwa mahali fulani kwenye wigo wa machungwa-kijani, jambo ambalo halionyeshi upendeleo halisi wa kundi lolote. Hata hivyo, hali ingekuwa mojawapo ya rangi hizo, au rangi zote mbili, ikiwa idadi ya watu wanaopendelea kila moja ni sawa (katika kesi hii tunaita sampuli multimodal).

Data Halisi

Tunapochambua data kutoka maisha halisi, mara nyingi si mabadiliko ya kawaida kama hayo, kwa maana kwamba hatufanyi majaribio yenye matokeo yasiyojulikana. Kwa mfano, fikiria timu ya wachezaji wa baseball, na data zao za mwili, kama vile urefu, uzito na umri. Namba hizo si za kubahatisha hasa, lakini bado tunaweza kutumia dhana zile zile za hisabati. Kwa mfano, mfuatano wa uzito wa watu unaweza kuchukuliwa kuwa mfuatano wa thamani zinazotolewa kutoka kwa mabadiliko fulani ya kawaida. Hapa chini ni mfuatano wa uzito wa wachezaji halisi wa baseball kutoka Major League Baseball, uliotolewa kutoka hifadhidata hii (kwa urahisi wako, ni thamani 20 za kwanza tu zimeonyeshwa):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Kumbuka: Ili kuona mfano wa kufanya kazi na hifadhidata hii, angalia notebook inayofuatana. Pia kuna changamoto kadhaa katika somo hili, na unaweza kuzimaliza kwa kuongeza msimbo kwenye notebook hiyo. Ikiwa huna uhakika jinsi ya kufanya kazi na data, usijali - tutarudi kwenye kufanya kazi na data kwa kutumia Python baadaye. Ikiwa hujui jinsi ya kuendesha msimbo kwenye Jupyter Notebook, angalia makala hii.

Hapa kuna mchoro wa box plot unaoonyesha wastani, median na robo kwa data yetu:

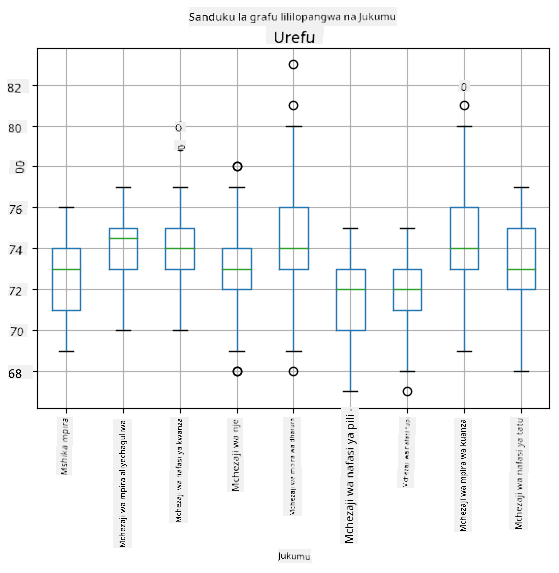
Kwa kuwa data yetu ina taarifa kuhusu majukumu tofauti ya wachezaji, tunaweza pia kufanya box plot kwa mujibu wa jukumu - hii itaturuhusu kupata wazo la jinsi thamani zinavyotofautiana kati ya majukumu. Wakati huu tutazingatia urefu:

Mchoro huu unaonyesha kwamba, kwa wastani, urefu wa wachezaji wa nafasi ya kwanza ni mrefu zaidi kuliko wa nafasi ya pili. Baadaye katika somo hili tutajifunza jinsi tunavyoweza kuthibitisha dhana hii kwa njia rasmi zaidi, na jinsi ya kuonyesha kwamba data yetu ni muhimu kitaalamu kuonyesha hilo.

Tunapofanya kazi na data halisi, tunadhani kwamba pointi zote za data ni sampuli zilizotolewa kutoka kwa usambazaji fulani wa uwezekano. Dhana hii inaturuhusu kutumia mbinu za kujifunza kwa mashine na kujenga mifano ya utabiri inayofanya kazi.

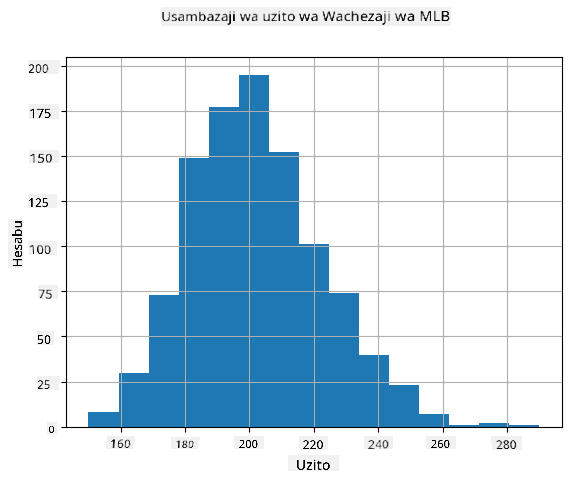
Ili kuona usambazaji wa data yetu, tunaweza kuchora mchoro unaoitwa histogramu. Mhimili wa X ungekuwa na idadi ya vipengele tofauti vya uzito (vinavyoitwa bins), na mhimili wa wima ungeonyesha idadi ya mara mabadiliko yetu ya kawaida yalikuwa ndani ya kipengele fulani.

Kutoka kwenye histogramu hii unaweza kuona kwamba thamani zote ziko katikati ya wastani fulani wa uzito, na kadri tunavyoenda mbali na uzito huo - ndivyo uzito wa thamani hiyo unavyopungua. Yaani, ni nadra sana kwamba uzito wa mchezaji wa baseball utakuwa tofauti sana na wastani wa uzito. Tofauti ya uzito inaonyesha kiwango ambacho uzito unaweza kutofautiana na wastani.

Tukichukua uzito wa watu wengine, si kutoka kwenye ligi ya baseball, usambazaji unaweza kuwa tofauti. Hata hivyo, umbo la usambazaji litakuwa sawa, lakini wastani na tofauti zitabadilika. Kwa hivyo, tukifundisha mfano wetu kwa wachezaji wa baseball, kuna uwezekano wa kutoa matokeo yasiyo sahihi unapowekwa kwa wanafunzi wa chuo kikuu, kwa sababu usambazaji wa msingi ni tofauti.

Usambazaji wa Kawaida

Usambazaji wa uzito ambao tumeona hapo juu ni wa kawaida sana, na vipimo vingi kutoka maisha halisi hufuata aina hiyo ya usambazaji, lakini na wastani na tofauti tofauti. Usambazaji huu unaitwa usambazaji wa kawaida, na una jukumu muhimu sana katika takwimu.

Kutumia usambazaji wa kawaida ni njia sahihi ya kuzalisha uzito wa kubahatisha wa wachezaji wa baseball wa baadaye. Mara tu tunapojua wastani wa uzito mean na mkengeuko wa kawaida std, tunaweza kuzalisha sampuli 1000 za uzito kwa njia ifuatayo:

samples = np.random.normal(mean,std,1000)

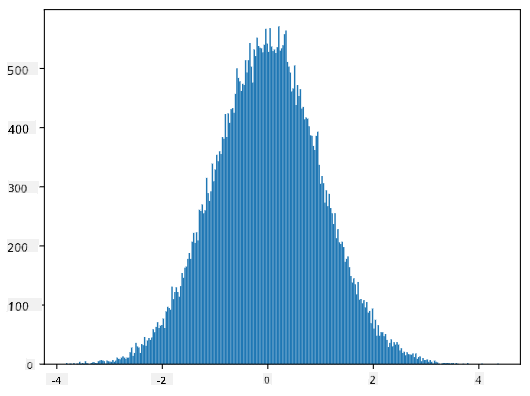
Tukichora histogramu ya sampuli zilizozalishwa tutaona picha inayofanana sana na ile iliyoonyeshwa hapo juu. Na tukiongeza idadi ya sampuli na idadi ya bins, tunaweza kuzalisha picha ya usambazaji wa kawaida inayokaribia ile bora zaidi:

Usambazaji wa Kawaida na wastani=0 na std.dev=1

Vipengele vya Uhakika

Tunapozungumzia uzito wa wachezaji wa baseball, tunadhani kwamba kuna mabadiliko ya kawaida W yanayowakilisha usambazaji bora wa uwezekano wa uzito wa wachezaji wote wa baseball (inayoitwa idadi ya watu). Mfuatano wetu wa uzito unawakilisha sehemu ndogo ya wachezaji wote wa baseball tunayoita sampuli. Swali la kuvutia ni, je, tunaweza kujua vigezo vya usambazaji wa W, yaani wastani na tofauti ya idadi ya watu?

Jibu rahisi litakuwa kuhesabu wastani na tofauti ya sampuli yetu. Hata hivyo, inaweza kutokea kwamba sampuli yetu ya kubahatisha haiwakilishi kwa usahihi idadi kamili ya watu. Kwa hivyo inafaa kuzungumzia kipengele cha uhakika.

Kipengele cha uhakika ni makadirio ya wastani wa kweli wa idadi ya watu kwa kuzingatia sampuli yetu, ambayo ni sahihi kwa uwezekano fulani (au kiwango cha uhakika).

Tuseme tuna sampuli X...

1, ..., X_n kutoka kwa usambazaji wetu. Kila mara tunapochukua sampuli kutoka kwa usambazaji wetu, tunapata thamani tofauti ya wastani μ. Kwa hivyo, μ inaweza kuchukuliwa kama kiashiria cha nasibu. Kiwango cha kujiamini chenye kujiamini p ni jozi ya thamani (L_p,R_p), ambapo P(L_p≤μ≤R_p) = p, yaani, uwezekano wa thamani ya wastani kupatikana ndani ya kiwango hicho ni sawa na p.

Inazidi maelezo mafupi yetu kujadili kwa undani jinsi viwango hivyo vya kujiamini vinavyohesabiwa. Maelezo zaidi yanaweza kupatikana kwenye Wikipedia. Kwa ufupi, tunafafanua usambazaji wa wastani wa sampuli uliohesabiwa kulingana na wastani halisi wa idadi ya watu, unaoitwa usambazaji wa mwanafunzi.

Ukweli wa kuvutia: Usambazaji wa mwanafunzi umepewa jina la mwanahisabati William Sealy Gosset, ambaye alichapisha karatasi yake kwa jina la bandia "Student". Alifanya kazi katika kiwanda cha bia cha Guinness, na, kulingana na mojawapo ya matoleo, mwajiri wake hakutaka umma kujua kwamba walikuwa wakitumia majaribio ya takwimu kuamua ubora wa malighafi.

Ikiwa tunataka kukadiria wastani μ wa idadi yetu ya watu kwa kujiamini p, tunahitaji kuchukua (1-p)/2-th percentile ya usambazaji wa mwanafunzi A, ambayo inaweza kuchukuliwa kutoka kwenye jedwali, au kuhesabiwa kwa kutumia baadhi ya kazi zilizojengwa ndani ya programu za takwimu (mfano Python, R, nk.). Kisha kiwango cha μ kitakuwa X±A*D/√n, ambapo X ni wastani uliopatikana wa sampuli, D ni kiwango cha mkengeuko.

Kumbuka: Tunapuuza pia mjadala wa dhana muhimu ya digrii za uhuru, ambayo ni muhimu kuhusiana na usambazaji wa mwanafunzi. Unaweza kurejelea vitabu kamili zaidi vya takwimu ili kuelewa dhana hii kwa undani.

Mfano wa kuhesabu kiwango cha kujiamini kwa uzito na urefu umetolewa katika majarida yanayoambatana.

p	Wastani wa Uzito
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Angalia kwamba kadri uwezekano wa kujiamini unavyoongezeka, ndivyo kiwango cha kujiamini kinavyopanuka.

Upimaji wa Dhana

Katika seti yetu ya data ya wachezaji wa baseball, kuna majukumu tofauti ya wachezaji, ambayo yanaweza kufupishwa hapa chini (angalia majarida yanayoambatana ili kuona jinsi jedwali hili linavyoweza kuhesabiwa):

Jukumu	Urefu	Uzito	Idadi
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

Tunaweza kuona kwamba wastani wa urefu wa first basemen ni mkubwa kuliko wa second basemen. Kwa hivyo, tunaweza kushawishika kusema kwamba first basemen ni warefu kuliko second basemen.

Kauli hii inaitwa dhana, kwa sababu hatujui kama ukweli huu ni sahihi au la.

Hata hivyo, si mara zote ni wazi ikiwa tunaweza kufanya hitimisho hili. Kutoka kwa mjadala hapo juu tunajua kwamba kila wastani una kiwango cha kujiamini kinachohusiana, na kwa hivyo tofauti hii inaweza kuwa tu kosa la takwimu. Tunahitaji njia rasmi zaidi ya kupima dhana yetu.

Hebu tuhesabu viwango vya kujiamini kando kwa urefu wa first na second basemen:

Kujiamini	First Basemen	Second Basemen
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Tunaweza kuona kwamba chini ya kiwango chochote cha kujiamini viwango havingiliani. Hii inathibitisha dhana yetu kwamba first basemen ni warefu kuliko second basemen.

Kwa njia rasmi zaidi, tatizo tunalotatua ni kuona kama usambazaji mbili za uwezekano ni sawa, au angalau zina vigezo sawa. Kulingana na usambazaji, tunahitaji kutumia majaribio tofauti kwa hilo. Ikiwa tunajua kwamba usambazaji wetu ni wa kawaida, tunaweza kutumia Student t-test.

Katika Student t-test, tunahesabu kinachoitwa t-value, ambacho kinaonyesha tofauti kati ya wastani, kwa kuzingatia mkengeuko. Imeonyeshwa kwamba t-value inafuata usambazaji wa mwanafunzi, ambao huturuhusu kupata thamani ya kizingiti kwa kiwango cha kujiamini p (hii inaweza kuhesabiwa, au kuangaliwa kwenye jedwali za nambari). Kisha tunalinganisha t-value na kizingiti hiki ili kuidhinisha au kukataa dhana.

Katika Python, tunaweza kutumia kifurushi cha SciPy, ambacho kinajumuisha kazi ya ttest_ind (pamoja na kazi nyingine nyingi muhimu za takwimu!). Inahesabu t-value kwa ajili yetu, na pia inafanya utafutaji wa kinyume wa p-value ya kujiamini, ili tuweze kuangalia tu kujiamini ili kufanya hitimisho.

Kwa mfano, kulinganisha kwetu kati ya urefu wa first na second basemen kunatupa matokeo yafuatayo:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

Katika kesi yetu, p-value ni ndogo sana, ikimaanisha kwamba kuna ushahidi mkubwa unaounga mkono kwamba first basemen ni warefu.

Kuna aina nyingine tofauti za dhana ambazo tunaweza kutaka kupima, kwa mfano:

Kuthibitisha kwamba sampuli fulani inafuata usambazaji fulani. Katika kesi yetu tumedhani kwamba urefu umegawanywa kawaida, lakini hiyo inahitaji uthibitisho rasmi wa takwimu.
Kuthibitisha kwamba thamani ya wastani wa sampuli inalingana na thamani fulani iliyowekwa
Kulinganisha wastani wa idadi ya sampuli (mfano, tofauti ya viwango vya furaha kati ya makundi tofauti ya umri)

Sheria ya Nambari Kubwa na Theoremu ya Kikomo cha Kati

Moja ya sababu kwa nini usambazaji wa kawaida ni muhimu ni kinachoitwa theoremu ya kikomo cha kati. Tuseme tuna sampuli kubwa ya N ya thamani huru X₁, ..., X_N, zilizochukuliwa kutoka kwa usambazaji wowote wenye wastani μ na mkengeuko σ². Kisha, kwa N kubwa ya kutosha (kwa maneno mengine, wakati N→∞), wastani Σ_iX_i utakuwa umegawanywa kawaida, na wastani μ na mkengeuko σ²/N.

Njia nyingine ya kufasiri theoremu ya kikomo cha kati ni kusema kwamba bila kujali usambazaji, unapohesabu wastani wa jumla ya thamani yoyote ya nasibu unapata usambazaji wa kawaida.

Kutoka kwa theoremu ya kikomo cha kati pia inafuata kwamba, wakati N→∞, uwezekano wa wastani wa sampuli kuwa sawa na μ unakuwa 1. Hii inajulikana kama sheria ya nambari kubwa.

Uhusiano wa Pamoja na Uwiano

Moja ya mambo ambayo Sayansi ya Takwimu hufanya ni kutafuta uhusiano kati ya data. Tunaposema kwamba mfululizo miwili ina uhusiano wa pamoja tunamaanisha kwamba inaonyesha tabia sawa kwa wakati mmoja, yaani, ama inapanda/inaanguka kwa pamoja, au mfululizo mmoja unapanda wakati mwingine unashuka na kinyume chake. Kwa maneno mengine, kunaonekana kuwa na uhusiano fulani kati ya mfululizo miwili.

Uhusiano wa pamoja hauonyeshi lazima uhusiano wa kisababishi kati ya mfululizo miwili; wakati mwingine vigezo vyote vinaweza kutegemea sababu ya nje, au inaweza kuwa tu kwa bahati kwamba mfululizo miwili una uhusiano wa pamoja. Hata hivyo, uhusiano wa pamoja wa kihisabati wenye nguvu ni kiashiria kizuri kwamba vigezo viwili vimeunganishwa kwa namna fulani.

Kihisabati, dhana kuu inayonyesha uhusiano kati ya vigezo viwili vya nasibu ni uhusiano wa pamoja, ambao unahesabiwa kama hivi: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Tunahesabu mkengeuko wa vigezo vyote kutoka kwa wastani wao, kisha tunazidisha mkengeuko huo. Ikiwa vigezo vyote vinapotosha pamoja, kuzidisha kutakuwa na thamani chanya kila mara, ambayo itaongeza hadi uhusiano wa pamoja chanya. Ikiwa vigezo vyote vinapotosha bila mpangilio (yaani, moja linashuka chini ya wastani wakati lingine linapanda juu ya wastani), tutapata namba hasi kila mara, ambayo itaongeza hadi uhusiano wa pamoja hasi. Ikiwa mkengeuko hauhusiani, utaongeza hadi takriban sifuri.

Thamani halisi ya uhusiano wa pamoja haituambii mengi kuhusu ukubwa wa uhusiano wa pamoja, kwa sababu inategemea ukubwa wa thamani halisi. Ili kuifanya iwe ya kawaida, tunaweza kugawanya uhusiano wa pamoja kwa mkengeuko wa kawaida wa vigezo vyote, ili kupata uwiano. Jambo zuri ni kwamba uwiano daima uko katika safu ya [-1,1], ambapo 1 inaonyesha uhusiano wa pamoja chanya kati ya thamani, -1 - uhusiano wa pamoja hasi wenye nguvu, na 0 - hakuna uhusiano wa pamoja kabisa (vigezo ni huru).

Mfano: Tunaweza kuhesabu uwiano kati ya uzito na urefu wa wachezaji wa baseball kutoka kwa seti ya data iliyotajwa hapo juu:

print(np.corrcoef(weights,heights))

Matokeo yake, tunapata matrix ya uwiano kama hii:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Matrix ya uwiano C inaweza kuhesabiwa kwa idadi yoyote ya mfululizo wa pembejeo S₁, ..., S_n. Thamani ya C_ij ni uwiano kati ya S_i na S_j, na vipengele vya diagonal daima ni 1 (ambayo pia ni uwiano wa pamoja wa S_i).

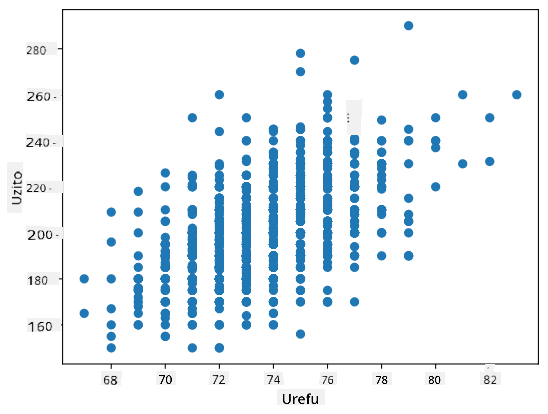
Katika kesi yetu, thamani 0.53 inaonyesha kwamba kuna uhusiano fulani kati ya uzito na urefu wa mtu. Tunaweza pia kutengeneza mchoro wa kutawanyika wa thamani moja dhidi ya nyingine ili kuona uhusiano kwa macho:

Mifano zaidi ya uwiano wa pamoja na uhusiano wa pamoja inaweza kupatikana katika majarida yanayoambatana.

Hitimisho

Katika sehemu hii, tumejifunza:

mali za msingi za takwimu za data, kama vile wastani, mkengeuko, hali na robo
usambazaji tofauti wa vigezo vya nasibu, ikiwa ni pamoja na usambazaji wa kawaida
jinsi ya kupata uwiano kati ya mali tofauti
jinsi ya kutumia mbinu za hisabati na takwimu ili kuthibitisha dhana fulani,
jinsi ya kuhesabu viwango vya kujiamini kwa kigezo cha nasibu kwa kuzingatia sampuli ya data

Ingawa hii si orodha kamili ya mada zilizopo ndani ya uwezekano na takwimu, inapaswa kuwa ya kutosha kukupa mwanzo mzuri katika kozi hii.

🚀 Changamoto

Tumia msimbo wa sampuli katika jarida kujaribu dhana nyingine kwamba:

First basemen ni wazee kuliko second basemen
First basemen ni warefu kuliko third basemen
Shortstops ni warefu kuliko second basemen

Maswali ya baada ya somo

Mapitio na Kujisomea

Uwezekano na takwimu ni mada pana sana inayostahili kozi yake yenyewe. Ikiwa una nia ya kwenda zaidi katika nadharia, unaweza kuendelea kusoma baadhi ya vitabu vifuatavyo:

Carlos Fernandez-Granda kutoka Chuo Kikuu cha New York ana maelezo mazuri ya mihadhara Probability and Statistics for Data Science (inapatikana mtandaoni)
Peter na Andrew Bruce. Practical Statistics for Data Scientists. [msimbo wa sampuli katika R].
James D. Miller. Statistics for Data Science [msimbo wa sampuli katika R]

Kazi

Utafiti Mdogo wa Kisukari

Credits

Somu hili limeandikwa kwa ♥️ na Dmitry Soshnikov

Kanusho:
Hati hii imetafsiriwa kwa kutumia huduma ya tafsiri ya AI Co-op Translator. Ingawa tunajitahidi kwa usahihi, tafadhali fahamu kuwa tafsiri za kiotomatiki zinaweza kuwa na makosa au kutokuwa sahihi. Hati ya asili katika lugha yake ya awali inapaswa kuzingatiwa kama chanzo cha mamlaka. Kwa taarifa muhimu, inashauriwa kutumia huduma ya tafsiri ya kitaalamu ya binadamu. Hatutawajibika kwa maelewano mabaya au tafsiri zisizo sahihi zinazotokana na matumizi ya tafsiri hii.

24 KiB Raw Permalink Blame History Unescape Escape