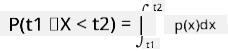24 KiB

Raw Permalink Blame History Unescape Escape

Kratek uvod v statistiko in verjetnost


Statistika in verjetnost - Sketchnote avtorja @nitya

Teorija statistike in verjetnosti sta dve tesno povezani področji matematike, ki sta zelo pomembni za podatkovno znanost. Čeprav je mogoče delati s podatki brez poglobljenega matematičnega znanja, je vseeno koristno poznati vsaj osnovne koncepte. Tukaj bomo predstavili kratek uvod, ki vam bo pomagal začeti.

Predavanje - kviz

Verjetnost in naključne spremenljivke

Verjetnost je število med 0 in 1, ki izraža, kako verjeten je določen dogodek. Definirana je kot število pozitivnih izidov (ki vodijo do dogodka), deljeno s skupnim številom možnih izidov, ob predpostavki, da so vsi izidi enako verjetni. Na primer, ko vržemo kocko, je verjetnost, da dobimo sodo število, 3/6 = 0,5.

Ko govorimo o dogodkih, uporabljamo naključne spremenljivke. Na primer, naključna spremenljivka, ki predstavlja število, dobljeno pri metanju kocke, bi imela vrednosti od 1 do 6. Množica števil od 1 do 6 se imenuje vzorec. Lahko govorimo o verjetnosti, da naključna spremenljivka dobi določeno vrednost, na primer P(X=3)=1/6.

Naključna spremenljivka v prejšnjem primeru se imenuje diskretna, ker ima števno vzorčno množico, tj. obstajajo ločene vrednosti, ki jih lahko naštejemo. Obstajajo pa tudi primeri, ko je vzorčna množica razpon realnih števil ali celotna množica realnih števil. Takšne spremenljivke imenujemo zvezne. Dober primer je čas prihoda avtobusa.

Porazdelitev verjetnosti

V primeru diskretnih naključnih spremenljivk je enostavno opisati verjetnost vsakega dogodka s funkcijo P(X). Za vsako vrednost s iz vzorčne množice S bo podala število med 0 in 1, tako da bo vsota vseh vrednosti P(X=s) za vse dogodke enaka 1.

Najbolj znana diskretna porazdelitev je enakomerna porazdelitev, pri kateri ima vzorčna množica N elementov, z enako verjetnostjo 1/N za vsakega od njih.

Težje je opisati porazdelitev verjetnosti zvezne spremenljivke, katere vrednosti so izbrane iz intervala [a,b] ali celotne množice realnih števil ℝ. Razmislimo o primeru časa prihoda avtobusa. Pravzaprav je za vsak točen čas prihoda t verjetnost, da avtobus pride točno ob tem času, enaka 0!

Zdaj veste, da se dogodki z verjetnostjo 0 zgodijo, in to zelo pogosto! Vsaj vsakič, ko avtobus prispe!

Lahko govorimo le o verjetnosti, da spremenljivka pade v določen interval vrednosti, npr. P(t₁≤X<t₂). V tem primeru je porazdelitev verjetnosti opisana z gostotno funkcijo verjetnosti p(x), tako da

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Zvezni analog enakomerne porazdelitve se imenuje zvezna enakomerna porazdelitev, ki je definirana na končnem intervalu. Verjetnost, da vrednost X pade v interval dolžine l, je sorazmerna z l in se povečuje do 1.

Druga pomembna porazdelitev je normalna porazdelitev, o kateri bomo podrobneje govorili spodaj.

Povprečje, varianca in standardni odklon

Predpostavimo, da vzamemo zaporedje n vzorcev naključne spremenljivke X: x₁, x₂, ..., x_n. Povprečje (ali aritmetična sredina) zaporedja lahko definiramo na tradicionalen način kot (x₁+x₂+...+x_n)/n. Ko povečujemo velikost vzorca (tj. vzamemo mejo pri n→∞), dobimo povprečje (imenovano tudi pričakovana vrednost) porazdelitve. Pričakovano vrednost označimo z E(x).

Dokazano je, da za katerokoli diskretno porazdelitev z vrednostmi {x₁, x₂, ..., x_N} in ustreznimi verjetnostmi p₁, p₂, ..., p_N, pričakovana vrednost ustreza E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Za ugotavljanje, kako razpršene so vrednosti, lahko izračunamo varianco σ² = ∑(x_i - μ)²/n, kjer je μ povprečje zaporedja. Vrednost σ imenujemo standardni odklon, σ² pa varianca.

Modus, mediana in kvartili

Včasih povprečje ne predstavlja ustrezno "tipične" vrednosti za podatke. Na primer, kadar obstajajo ekstremne vrednosti, ki so povsem izven dosega, lahko vplivajo na povprečje. Druga dobra mera je mediana, vrednost, pri kateri je polovica podatkov nižja, druga polovica pa višja.

Za boljše razumevanje porazdelitve podatkov je koristno govoriti o kvartilih:

Prvi kvartil ali Q1 je vrednost, pri kateri je 25 % podatkov nižjih od nje.
Tretji kvartil ali Q3 je vrednost, pri kateri je 75 % podatkov nižjih od nje.

Grafično lahko razmerje med mediano in kvartili predstavimo v diagramu, imenovanem škatlasti diagram:

Tukaj prav tako izračunamo interkvartilni razpon IQR=Q3-Q1 in tako imenovane izstopajoče vrednosti - vrednosti, ki ležijo zunaj meja [Q1-1.5IQR, Q3+1.5IQR].

Za končno porazdelitev, ki vsebuje majhno število možnih vrednosti, je dobra "tipična" vrednost tista, ki se pojavi najpogosteje, in jo imenujemo modus. Pogosto se uporablja za kategorialne podatke, kot so barve. Na primer, če imamo dve skupini ljudi - eno, ki močno preferira rdečo, in drugo, ki preferira modro. Če barve kodiramo s številkami, bi povprečna vrednost za najljubšo barvo padla nekje v oranžno-zeleni spekter, kar ne bi ustrezalo dejanskim preferencam nobene skupine. Modus pa bi bil ena od barv ali obe barvi, če je število ljudi, ki glasujejo za njiju, enako (v tem primeru vzorec imenujemo multimodalen).

Podatki iz resničnega sveta

Ko analiziramo podatke iz resničnega življenja, ti pogosto niso naključne spremenljivke v pravem pomenu besede, saj ne izvajamo eksperimentov z neznanim izidom. Na primer, razmislimo o ekipi igralcev baseballa in njihovih telesnih podatkih, kot so višina, teža in starost. Te številke niso povsem naključne, vendar lahko še vedno uporabimo iste matematične koncepte. Na primer, zaporedje tež igralcev lahko obravnavamo kot zaporedje vrednosti, izbranih iz neke naključne spremenljivke. Spodaj je zaporedje tež dejanskih igralcev baseballa iz Major League Baseball, vzeto iz tega nabora podatkov (za vašo udobje je prikazanih le prvih 20 vrednosti):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Opomba: Če želite videti primer dela s tem naborom podatkov, si oglejte priloženi zvezek. V tej lekciji je tudi več izzivov, ki jih lahko rešite z dodajanjem kode v ta zvezek. Če niste prepričani, kako delati s podatki, ne skrbite - k delu s podatki v Pythonu se bomo vrnili kasneje. Če ne veste, kako zagnati kodo v Jupyter Notebooku, si oglejte ta članek.

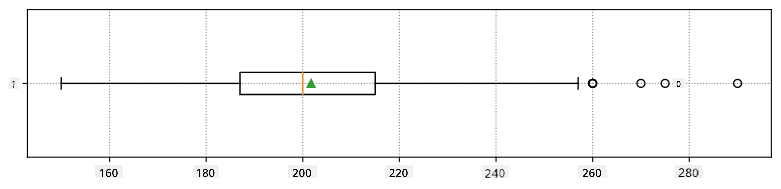
Tukaj je škatlasti diagram, ki prikazuje povprečje, mediano in kvartile za naše podatke:

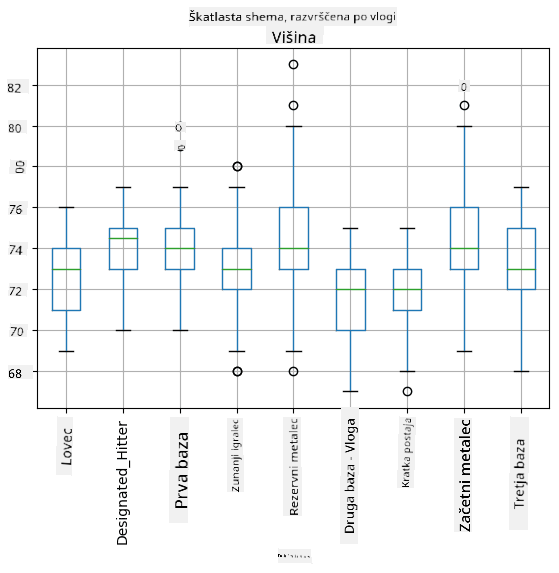
Ker naši podatki vsebujejo informacije o različnih vlogah igralcev, lahko naredimo tudi škatlasti diagram po vlogah - to nam omogoča vpogled v to, kako se vrednosti parametrov razlikujejo med vlogami. Tokrat bomo obravnavali višino:

Ta diagram nakazuje, da je povprečna višina igralcev na prvi bazi višja od višine igralcev na drugi bazi. Kasneje v tej lekciji se bomo naučili, kako lahko to hipotezo formalneje preverimo in kako pokažemo, da so naši podatki statistično pomembni za to trditev.

Pri delu s podatki iz resničnega sveta predpostavljamo, da so vse točke vzorci, izbrani iz neke porazdelitve verjetnosti. Ta predpostavka nam omogoča uporabo tehnik strojnega učenja in gradnjo delujočih napovednih modelov.

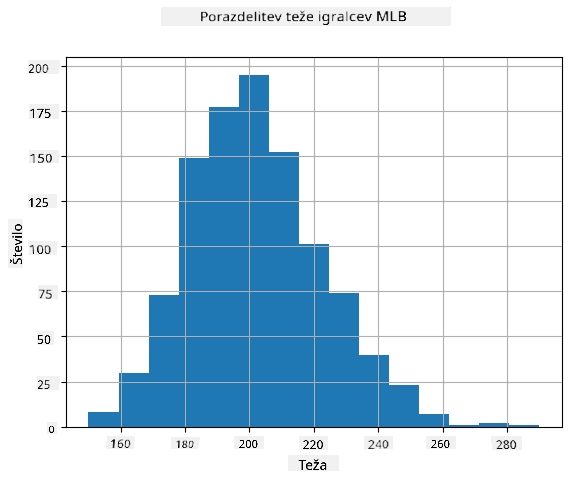
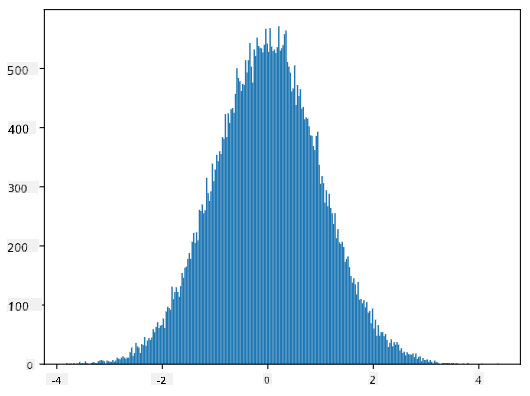
Da bi videli, kakšna je porazdelitev naših podatkov, lahko narišemo graf, imenovan histogram. X-os bo vsebovala število različnih intervalov teže (tako imenovanih razredov), Y-os pa bo prikazovala število primerov, ko je vzorec naključne spremenljivke padel v določen interval.

Iz tega histograma lahko vidimo, da so vse vrednosti skoncentrirane okoli določenega povprečja teže, in bolj ko se oddaljujemo od tega povprečja, manj pogosto se pojavljajo teže te vrednosti. To pomeni, da je zelo malo verjetno, da bi bila teža igralca baseballa zelo različna od povprečne teže. Varianca tež prikazuje, v kolikšni meri se teže verjetno razlikujejo od povprečja.

Če bi vzeli teže drugih ljudi, ki niso iz baseball lige, bi bila porazdelitev verjetno drugačna. Vendar bi bila oblika porazdelitve enaka, le povprečje in varianca bi se spremenila. Če torej naš model treniramo na igralcih baseballa, bo verjetno dal napačne rezultate, ko ga uporabimo na študentih univerze, ker je osnovna porazdelitev drugačna.

Normalna porazdelitev

Porazdelitev tež, ki smo jo videli zgoraj, je zelo tipična, in veliko meritev iz resničnega sveta sledi istemu tipu porazdelitve, vendar z različnim povprečjem in varianco. Ta porazdelitev se imenuje normalna porazdelitev in igra zelo pomembno vlogo v statistiki.

Uporaba normalne porazdelitve je pravilen način za generiranje naključnih tež potencialnih igralcev baseballa. Ko poznamo povprečno težo mean in standardni odklon std, lahko generiramo 1000 vzorcev teže na naslednji način:

samples = np.random.normal(mean,std,1000)

Če narišemo histogram generiranih vzorcev, bomo videli sliko, zelo podobno zgornji. Če povečamo število vzorcev in število razredov, lahko ustvarimo sliko normalne porazdelitve, ki je bližje idealni:

Normalna porazdelitev s povprečjem=0 in std.odklonom=1

Intervali zaupanja

Ko govorimo o težah igralcev baseballa, predpostavljamo, da obstaja določena naključna spremenljivka W, ki ustreza idealni porazdelitvi verjetnosti tež vseh igralcev baseballa (tako imenovana populacija). Naše zaporedje tež ustreza podmnožici vseh igralcev baseballa, ki jo imenujemo vzorec. Zanimivo vprašanje je, ali lahko poznamo parametre porazdelitve W, tj. povprečje in varianco populacije?

Najlažji odgovor bi bil izračunati povprečje in varianco našega vzorca. Vendar se lahko zgodi, da naš naključni vzorec ne predstavlja natančno celotne populacije. Zato je smiselno govoriti o intervalu zaupanja.

Interval zaupanja je ocena pravega povprečja populacije glede na naš vzorec, ki je točna z določeno verjetnostjo (ali stopnjo zaupanja).

Predpostavimo, da imamo vzorec X...

1, ..., X_n iz naše porazdelitve. Vsakič, ko vzamemo vzorec iz naše porazdelitve, dobimo drugačno povprečno vrednost μ. Tako lahko μ obravnavamo kot naključno spremenljivko. Interval zaupanja z zaupanjem p je par vrednosti (L_p,R_p), tako da P(L_p≤μ≤R_p) = p, torej verjetnost, da izmerjena povprečna vrednost pade v interval, je enaka p.

Podrobna razlaga, kako se ti intervali zaupanja izračunajo, presega naš kratek uvod. Več podrobnosti najdete na Wikipediji. Na kratko, definiramo porazdelitev izračunanega vzorčnega povprečja glede na pravo povprečje populacije, kar imenujemo studentova porazdelitev.

Zanimivo dejstvo: Studentova porazdelitev je poimenovana po matematiku Williamu Sealyju Gossetu, ki je svoje delo objavil pod psevdonimom "Student". Delal je v pivovarni Guinness, in po eni od različic njegov delodajalec ni želel, da bi širša javnost vedela, da uporabljajo statistične teste za določanje kakovosti surovin.

Če želimo oceniti povprečje μ naše populacije z zaupanjem p, moramo vzeti (1-p)/2-ti percentil studentove porazdelitve A, ki ga lahko pridobimo iz tabel ali izračunamo z vgrajenimi funkcijami statistične programske opreme (npr. Python, R itd.). Nato je interval za μ podan z X±A*D/√n, kjer je X pridobljeno povprečje vzorca, D pa standardni odklon.

Opomba: Prav tako izpuščamo razpravo o pomembnem konceptu stopnje prostosti, ki je pomemben v povezavi s studentovo porazdelitvijo. Za globlje razumevanje tega koncepta se lahko obrnete na bolj celovite knjige o statistiki.

Primer izračuna intervala zaupanja za težo in višino je podan v priloženih zvezkih.

p	Povprečje teže
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Opazimo, da je višja verjetnost zaupanja, širši je interval zaupanja.

Testiranje hipotez

V našem naboru podatkov o igralcih baseballa obstajajo različne vloge igralcev, ki jih lahko povzamemo spodaj (glejte priložen zvezek, da vidite, kako se ta tabela lahko izračuna):

Vloga	Višina	Teža	Število
Lovec	72.723684	204.328947	76
Določeni udarec	74.222222	220.888889	18
Prvi bazni igralec	74.000000	213.109091	55
Zunanji igralec	73.010309	199.113402	194
Rezervni metalec	74.374603	203.517460	315
Drugi bazni igralec	71.362069	184.344828	58
Kratki igralec	71.903846	182.923077	52
Začetni metalec	74.719457	205.163636	221
Tretji bazni igralec	73.044444	200.955556	45

Opazimo lahko, da je povprečna višina prvih baznih igralcev višja od povprečne višine drugih baznih igralcev. Tako bi lahko sklepali, da so prvi bazni igralci višji od drugih baznih igralcev.

Ta izjava se imenuje hipoteza, ker ne vemo, ali je dejstvo dejansko resnično ali ne.

Vendar ni vedno očitno, ali lahko to zaključimo. Iz zgornje razprave vemo, da ima vsako povprečje pripadajoči interval zaupanja, zato je lahko ta razlika zgolj statistična napaka. Potrebujemo bolj formalni način za testiranje naše hipoteze.

Izračunajmo intervale zaupanja ločeno za višine prvih in drugih baznih igralcev:

Zaupanje	Prvi bazni igralci	Drugi bazni igralci
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Vidimo, da se pri nobenem zaupanju intervali ne prekrivajo. To dokazuje našo hipotezo, da so prvi bazni igralci višji od drugih baznih igralcev.

Bolj formalno, problem, ki ga rešujemo, je ugotoviti, ali sta dve porazdelitvi verjetnosti enaki, ali imata vsaj enake parametre. Glede na porazdelitev moramo za to uporabiti različne teste. Če vemo, da sta naši porazdelitvi normalni, lahko uporabimo Studentov t-test.

Pri Studentovem t-testu izračunamo tako imenovano t-vrednost, ki kaže razliko med povprečji ob upoštevanju variance. Dokazano je, da t-vrednost sledi studentovi porazdelitvi, kar nam omogoča pridobitev mejne vrednosti za dano raven zaupanja p (to lahko izračunamo ali poiščemo v numeričnih tabelah). Nato primerjamo t-vrednost s to mejno vrednostjo, da potrdimo ali zavrnemo hipotezo.

V Pythonu lahko uporabimo paket SciPy, ki vključuje funkcijo ttest_ind (poleg mnogih drugih uporabnih statističnih funkcij!). Ta funkcija za nas izračuna t-vrednost in tudi obraten izračun p-vrednosti zaupanja, tako da lahko preprosto pogledamo zaupanje in sprejmemo zaključek.

Na primer, naša primerjava med višinami prvih in drugih baznih igralcev nam daje naslednje rezultate:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

V našem primeru je p-vrednost zelo nizka, kar pomeni, da obstajajo močni dokazi, ki podpirajo, da so prvi bazni igralci višji.

Obstajajo tudi različne druge vrste hipotez, ki jih morda želimo testirati, na primer:

Dokazati, da dani vzorec sledi neki porazdelitvi. V našem primeru smo predpostavili, da so višine normalno porazdeljene, vendar to zahteva formalno statistično preverjanje.
Dokazati, da povprečna vrednost vzorca ustreza neki predhodno določeni vrednosti.
Primerjati povprečja več vzorcev (npr. kakšna je razlika v ravni sreče med različnimi starostnimi skupinami).

Zakon velikih števil in centralni limitni izrek

Eden od razlogov, zakaj je normalna porazdelitev tako pomembna, je tako imenovani centralni limitni izrek. Predpostavimo, da imamo velik vzorec neodvisnih N vrednosti X₁, ..., X_N, vzorčenih iz katere koli porazdelitve s povprečjem μ in varianco σ². Nato, za dovolj veliko N (z drugimi besedami, ko N→∞), bo povprečje Σ_iX_i normalno porazdeljeno, s povprečjem μ in varianco σ²/N.

Drug način interpretacije centralnega limitnega izreka je, da ne glede na porazdelitev, ko izračunate povprečje vsote vrednosti katere koli naključne spremenljivke, dobite normalno porazdelitev.

Iz centralnega limitnega izreka prav tako sledi, da, ko N→∞, verjetnost, da bo vzorčno povprečje enako μ, postane 1. To je znano kot zakon velikih števil.

Kovarianca in korelacija

Ena od stvari, ki jih počne podatkovna znanost, je iskanje povezav med podatki. Pravimo, da se dve zaporedji korelirata, ko kažeta podobno vedenje ob istem času, tj. se bodisi hkrati dvigujeta/padata, bodisi eno zaporedje narašča, ko drugo pada, in obratno. Z drugimi besedami, zdi se, da obstaja neka povezava med dvema zaporedjema.

Korelacija ne pomeni nujno vzročne povezave med dvema zaporedjema; včasih lahko obe spremenljivki odvisni od nekega zunanjega vzroka, ali pa je zgolj naključje, da se dve zaporedji korelirata. Vendar pa je močna matematična korelacija dober pokazatelj, da sta dve spremenljivki nekako povezani.

Matematično je glavni koncept, ki kaže povezavo med dvema naključnima spremenljivkama, kovarianca, ki se izračuna takole: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Izračunamo odklon obeh spremenljivk od njihovih povprečnih vrednosti in nato produkt teh odklonov. Če obe spremenljivki odstopata skupaj, bo produkt vedno pozitivna vrednost, ki bo prispevala k pozitivni kovarianci. Če obe spremenljivki odstopata neusklajeno (tj. ena pade pod povprečje, ko druga naraste nad povprečje), bomo vedno dobili negativne številke, ki bodo prispevale k negativni kovarianci. Če odkloni niso odvisni, se bodo približno sešteli na nič.

Absolutna vrednost kovariance nam ne pove veliko o tem, kako velika je korelacija, ker je odvisna od velikosti dejanskih vrednosti. Da jo normaliziramo, lahko kovarianco delimo s standardnim odklonom obeh spremenljivk, da dobimo korelacijo. Dobro je, da je korelacija vedno v razponu [-1,1], kjer 1 označuje močno pozitivno korelacijo med vrednostmi, -1 močno negativno korelacijo, in 0 - nobene korelacije (spremenljivki sta neodvisni).

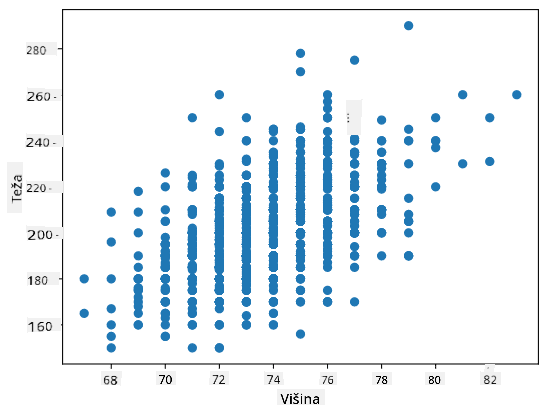
Primer: Korelacijo med težo in višino igralcev baseballa iz zgoraj omenjenega nabora podatkov lahko izračunamo:

print(np.corrcoef(weights,heights))

Kot rezultat dobimo korelacijsko matriko, kot je ta:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Korelacijsko matriko C lahko izračunamo za poljubno število vhodnih zaporedij S₁, ..., S_n. Vrednost C_ij je korelacija med S_i in S_j, diagonalni elementi pa so vedno 1 (kar je tudi samokorelacija S_i).

V našem primeru vrednost 0.53 kaže, da obstaja neka korelacija med težo in višino osebe. Prav tako lahko naredimo razpršeni diagram ene vrednosti proti drugi, da vizualno vidimo povezavo:

Več primerov korelacije in kovariance najdete v priloženem zvezku.

Zaključek

V tem poglavju smo se naučili:

osnovnih statističnih lastnosti podatkov, kot so povprečje, varianca, modus in kvartili
različnih porazdelitev naključnih spremenljivk, vključno z normalno porazdelitvijo
kako najti korelacijo med različnimi lastnostmi
kako uporabiti matematični in statistični aparat za dokazovanje hipotez
kako izračunati intervale zaupanja za naključno spremenljivko glede na vzorec podatkov

Čeprav to ni izčrpen seznam tem, ki obstajajo znotraj verjetnosti in statistike, bi moralo biti dovolj, da vam omogoči dober začetek tega tečaja.

🚀 Izziv

Uporabite vzorčno kodo v zvezku za testiranje drugih hipotez:

Prvi bazni igralci so starejši od drugih baznih igralcev
Prvi bazni igralci so višji od tretjih baznih igralcev
Kratki igralci so višji od drugih baznih igralcev

Kvizi po predavanju

Pregled in samostojno učenje

Verjetnost in statistika sta tako široki temi, da si zaslužita svoj tečaj. Če želite iti globlje v teorijo, lahko nadaljujete z branjem nekaterih naslednjih knjig:

Carlos Fernandez-Granda z New York University ima odlične zapiske predavanj Probability and Statistics for Data Science (na voljo na spletu)
Peter in Andrew Bruce. Practical Statistics for Data Scientists. [vzorec kode v R].
James D. Miller. Statistics for Data Science [vzorec kode v R]

Naloga

Majhna študija o diabetesu

Zasluge

To lekcijo je z ljubeznijo napisal Dmitry Soshnikov

Omejitev odgovornosti:
Ta dokument je bil preveden z uporabo storitve za strojno prevajanje Co-op Translator. Čeprav si prizadevamo za natančnost, vas prosimo, da se zavedate, da lahko avtomatizirani prevodi vsebujejo napake ali netočnosti. Izvirni dokument v njegovem izvirnem jeziku je treba obravnavati kot avtoritativni vir. Za ključne informacije priporočamo strokovno človeško prevajanje. Ne prevzemamo odgovornosti za morebitna nesporazumevanja ali napačne razlage, ki izhajajo iz uporabe tega prevoda.

24 KiB Raw Permalink Blame History Unescape Escape