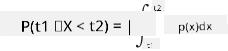32 KiB

Raw Permalink Blame History Unescape Escape

مقدمة موجزة في الإحصاء والاحتمالات


الإحصاء والاحتمالات - رسم توضيحي بواسطة @nitya

نظرية الإحصاء والاحتمالات هما مجالان مترابطان في الرياضيات ولهما أهمية كبيرة في علم البيانات. يمكن العمل مع البيانات دون معرفة عميقة بالرياضيات، ولكن من الأفضل معرفة بعض المفاهيم الأساسية على الأقل. هنا سنقدم مقدمة قصيرة لمساعدتك على البدء.

اختبار ما قبل المحاضرة

الاحتمالات والمتغيرات العشوائية

الاحتمال هو رقم بين 0 و1 يعبر عن مدى احتمال حدوث حدث معين. يتم تعريفه على أنه عدد النتائج الإيجابية (التي تؤدي إلى الحدث)، مقسومًا على العدد الإجمالي للنتائج، بشرط أن تكون جميع النتائج متساوية الاحتمال. على سبيل المثال، عند رمي النرد، فإن احتمال الحصول على رقم زوجي هو 3/6 = 0.5.

عندما نتحدث عن الأحداث، نستخدم المتغيرات العشوائية. على سبيل المثال، المتغير العشوائي الذي يمثل الرقم الناتج عند رمي النرد يأخذ قيمًا من 1 إلى 6. مجموعة الأرقام من 1 إلى 6 تُسمى فضاء العينة. يمكننا الحديث عن احتمال أن يأخذ المتغير العشوائي قيمة معينة، مثل P(X=3)=1/6.

المتغير العشوائي في المثال السابق يُسمى متغيرًا منفصلًا، لأنه يحتوي على فضاء عينة قابل للعد، أي أن هناك قيمًا منفصلة يمكن تعدادها. هناك حالات يكون فيها فضاء العينة عبارة عن نطاق من الأرقام الحقيقية، أو مجموعة الأرقام الحقيقية بأكملها. تُسمى هذه المتغيرات متصلة. مثال جيد هو وقت وصول الحافلة.

توزيع الاحتمالات

في حالة المتغيرات العشوائية المنفصلة، من السهل وصف احتمال كل حدث بواسطة دالة P(X). لكل قيمة s من فضاء العينة S، ستعطي رقمًا بين 0 و1، بحيث يكون مجموع جميع قيم P(X=s) لجميع الأحداث يساوي 1.

التوزيع المنفصل الأكثر شهرة هو التوزيع المنتظم، حيث يوجد فضاء عينة يحتوي على N عنصرًا، مع احتمال متساوٍ قدره 1/N لكل منها.

من الصعب وصف توزيع الاحتمالات للمتغير المتصل، مع قيم مأخوذة من بعض الفواصل [a,b]، أو مجموعة الأرقام الحقيقية ℝ. فكر في حالة وقت وصول الحافلة. في الواقع، بالنسبة لكل وقت وصول محدد t، فإن احتمال وصول الحافلة في ذلك الوقت بالضبط هو 0!

الآن تعرف أن الأحداث ذات الاحتمال 0 تحدث، وغالبًا جدًا! على الأقل في كل مرة تصل فيها الحافلة!

يمكننا فقط الحديث عن احتمال أن يقع المتغير في نطاق معين من القيم، مثل P(t₁≤X<t₂). في هذه الحالة، يتم وصف توزيع الاحتمالات بواسطة دالة كثافة الاحتمال p(x)، بحيث

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

النظير المتصل للتوزيع المنتظم يُسمى التوزيع المنتظم المتصل، والذي يتم تعريفه على فاصل محدود. احتمال أن تقع القيمة X في فاصل طوله l يتناسب مع l، ويصل إلى 1.

توزيع آخر مهم هو التوزيع الطبيعي، والذي سنتحدث عنه بمزيد من التفصيل أدناه.

المتوسط، التباين والانحراف المعياري

افترض أننا أخذنا سلسلة من n عينات من متغير عشوائي X: x₁, x₂, ..., x_n. يمكننا تعريف المتوسط (أو المتوسط الحسابي) للقيم في السلسلة بالطريقة التقليدية كالتالي: (x₁+x₂+x_n)/n. مع زيادة حجم العينة (أي أخذ الحد مع n→∞)، سنحصل على المتوسط (ويُسمى أيضًا التوقع) للتوزيع. سنرمز للتوقع بـ E(x).

يمكن إثبات أنه بالنسبة لأي توزيع منفصل بقيم {x₁, x₂, ..., x_N} واحتمالات مقابلة p₁, p₂, ..., p_N، فإن التوقع سيكون E(X)=x₁p₁+x₂p₂+...+x_Np_N.

لتحديد مدى انتشار القيم، يمكننا حساب التباين σ² = ∑(x_i - μ)²/n، حيث μ هو متوسط السلسلة. القيمة σ تُسمى الانحراف المعياري، وσ² تُسمى التباين.

النمط، الوسيط والرباعيات

في بعض الأحيان، لا يمثل المتوسط بشكل كافٍ القيمة "النموذجية" للبيانات. على سبيل المثال، عندما تكون هناك بعض القيم المتطرفة التي تكون خارج النطاق تمامًا، يمكن أن تؤثر على المتوسط. مؤشر جيد آخر هو الوسيط، وهو قيمة بحيث تكون نصف نقاط البيانات أقل منها، والنصف الآخر أعلى.

لمساعدتنا في فهم توزيع البيانات، من المفيد الحديث عن الرباعيات:

الربعية الأولى، أو Q1، هي قيمة بحيث تقع 25% من البيانات تحتها
الربعية الثالثة، أو Q3، هي قيمة بحيث تقع 75% من البيانات تحتها

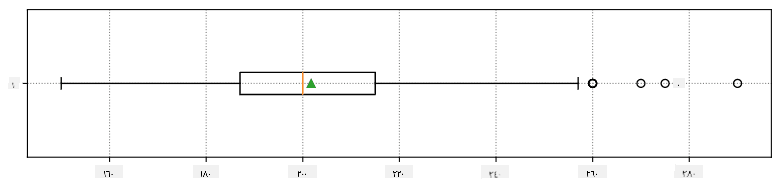
يمكننا تمثيل العلاقة بين الوسيط والرباعيات في رسم بياني يُسمى مخطط الصندوق:

هنا نحسب أيضًا النطاق بين الرباعيات IQR=Q3-Q1، وما يُسمى القيم المتطرفة - وهي القيم التي تقع خارج الحدود [Q1-1.5IQR,Q3+1.5IQR].

بالنسبة للتوزيع المحدود الذي يحتوي على عدد صغير من القيم الممكنة، فإن القيمة "النموذجية" الجيدة هي تلك التي تظهر بشكل متكرر، والتي تُسمى النمط. غالبًا ما يتم تطبيقه على البيانات الفئوية، مثل الألوان. فكر في حالة وجود مجموعتين من الأشخاص - بعضهم يفضل الأحمر بشدة، والبعض الآخر يفضل الأزرق. إذا قمنا بترميز الألوان بأرقام، فإن القيمة المتوسطة للون المفضل ستكون في نطاق البرتقالي-الأخضر، مما لا يعكس التفضيل الفعلي لأي من المجموعتين. ومع ذلك، سيكون النمط إما أحد الألوان، أو كلاهما إذا كان عدد الأشخاص الذين يفضلونها متساويًا (في هذه الحالة نسمي العينة متعددة الأنماط).

البيانات الواقعية

عند تحليل البيانات من الحياة الواقعية، غالبًا ما تكون هذه البيانات ليست متغيرات عشوائية بالمعنى الدقيق، بمعنى أننا لا نجري تجارب بنتائج غير معروفة. على سبيل المثال، فكر في فريق من لاعبي البيسبول، وبيانات أجسامهم مثل الطول، الوزن والعمر. هذه الأرقام ليست عشوائية تمامًا، ولكن يمكننا تطبيق نفس المفاهيم الرياضية. على سبيل المثال، يمكن اعتبار سلسلة أوزان الأشخاص سلسلة من القيم مأخوذة من متغير عشوائي معين. أدناه سلسلة أوزان لاعبي البيسبول الفعليين من دوري البيسبول الرئيسي، مأخوذة من هذه المجموعة (لراحتك، تم عرض أول 20 قيمة فقط):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

ملاحظة: لرؤية مثال على العمل مع هذه المجموعة، ألقِ نظرة على دفتر الملاحظات المرافق. هناك أيضًا عدد من التحديات طوال هذا الدرس، ويمكنك إكمالها بإضافة بعض التعليمات البرمجية إلى ذلك الدفتر. إذا كنت غير متأكد من كيفية العمل مع البيانات، لا تقلق - سنعود إلى العمل مع البيانات باستخدام Python لاحقًا. إذا كنت لا تعرف كيفية تشغيل التعليمات البرمجية في Jupyter Notebook، ألقِ نظرة على هذه المقالة.

إليك مخطط الصندوق الذي يظهر المتوسط، الوسيط والرباعيات لبياناتنا:

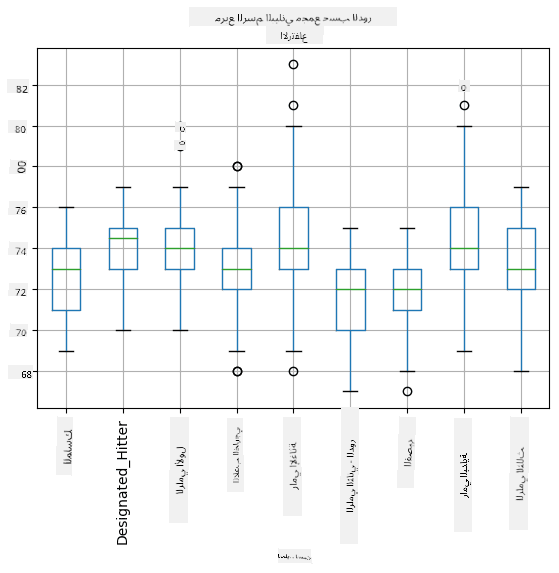
نظرًا لأن بياناتنا تحتوي على معلومات حول الأدوار المختلفة للاعبين، يمكننا أيضًا إنشاء مخطط الصندوق حسب الدور - مما يسمح لنا بفهم كيفية اختلاف قيم المعلمات عبر الأدوار. هذه المرة سننظر في الطول:

يشير هذا الرسم إلى أنه، في المتوسط، يكون طول لاعبي القاعدة الأولى أعلى من طول لاعبي القاعدة الثانية. لاحقًا في هذا الدرس، سنتعلم كيفية اختبار هذه الفرضية بشكل أكثر رسمية، وكيفية إثبات أن بياناتنا ذات دلالة إحصائية لإظهار ذلك.

عند العمل مع البيانات الواقعية، نفترض أن جميع نقاط البيانات هي عينات مأخوذة من توزيع احتمالي معين. يسمح لنا هذا الافتراض بتطبيق تقنيات التعلم الآلي وبناء نماذج تنبؤية فعالة.

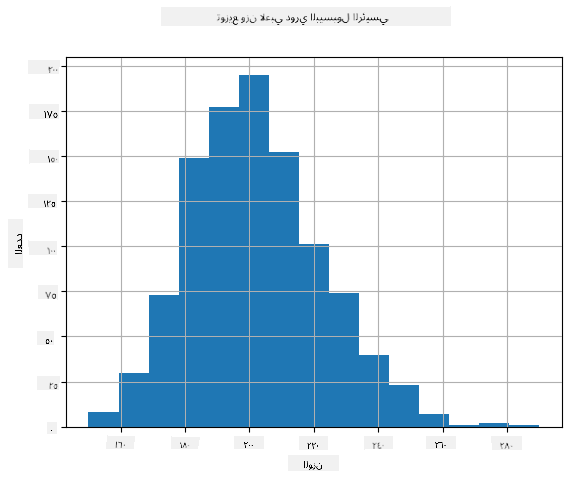
لرؤية توزيع بياناتنا، يمكننا رسم رسم بياني يُسمى الهيستوجرام. يحتوي المحور X على عدد من فواصل الوزن المختلفة (ما يُسمى الصناديق)، ويُظهر المحور العمودي عدد المرات التي كانت فيها عينة المتغير العشوائي داخل فاصل معين.

من هذا الهيستوجرام، يمكنك رؤية أن جميع القيم تتمركز حول متوسط وزن معين، وكلما ابتعدنا عن ذلك الوزن - قل عدد الأوزان التي لها تلك القيمة. أي أنه من غير المحتمل جدًا أن يكون وزن لاعب البيسبول مختلفًا جدًا عن متوسط الوزن. يظهر تباين الأوزان مدى احتمال اختلاف الأوزان عن المتوسط.

إذا أخذنا أوزان أشخاص آخرين، ليسوا من دوري البيسبول، فمن المحتمل أن يكون التوزيع مختلفًا. ومع ذلك، سيكون شكل التوزيع نفسه، ولكن المتوسط والتباين سيتغيران. لذا، إذا قمنا بتدريب نموذجنا على لاعبي البيسبول، فمن المحتمل أن يعطي نتائج خاطئة عند تطبيقه على طلاب الجامعة، لأن التوزيع الأساسي مختلف.

التوزيع الطبيعي

التوزيع الذي رأيناه أعلاه للأوزان هو شائع جدًا، والعديد من القياسات من العالم الواقعي تتبع نفس النوع من التوزيع، ولكن بمتوسط وتباين مختلفين. يُسمى هذا التوزيع التوزيع الطبيعي، ويلعب دورًا مهمًا جدًا في الإحصاء.

استخدام التوزيع الطبيعي هو الطريقة الصحيحة لتوليد أوزان عشوائية للاعبي البيسبول المحتملين. بمجرد أن نعرف متوسط الوزن mean والانحراف المعياري std، يمكننا توليد 1000 عينة وزن بالطريقة التالية:

samples = np.random.normal(mean,std,1000)

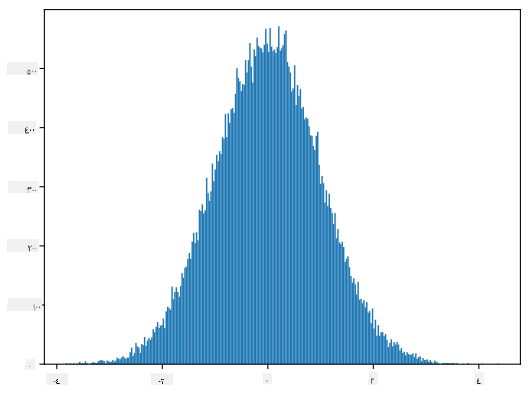
إذا قمنا برسم الهيستوجرام للعينات المولدة، سنرى صورة مشابهة جدًا لتلك الموضحة أعلاه. وإذا قمنا بزيادة عدد العينات وعدد الصناديق، يمكننا توليد صورة للتوزيع الطبيعي تكون أقرب إلى المثالية:

توزيع طبيعي بمتوسط=0 وانحراف معياري=1

فترات الثقة

عندما نتحدث عن أوزان لاعبي البيسبول، نفترض أن هناك متغير عشوائي W يمثل التوزيع الاحتمالي المثالي لأوزان جميع لاعبي البيسبول (ما يُسمى السكان). تتوافق سلسلة الأوزان الخاصة بنا مع مجموعة فرعية من جميع لاعبي البيسبول التي نسميها العينة. السؤال المثير للاهتمام هو، هل يمكننا معرفة معلمات توزيع W، أي متوسط وتباين السكان؟

الإجابة الأسهل ستكون حساب المتوسط والتباين لعينةنا. ومع ذلك، قد يحدث أن عينةنا العشوائية لا تمثل السكان بالكامل بدقة. لذلك من المنطقي الحديث عن فترة الثقة.

فترة الثقة هي تقدير المتوسط الحقيقي للسكان بناءً على عينةنا، والذي يكون دقيقًا بنسبة معينة (أو مستوى الثقة).

افترض أن لدينا عينة X <فرعي> 1, ..., X_n من توزيعنا. في كل مرة نأخذ عينة من توزيعنا، سنحصل على قيمة متوسط مختلفة μ. وبالتالي يمكن اعتبار μ متغيرًا عشوائيًا. فترة الثقة بمستوى ثقة p هي زوج من القيم (L_p,R_p)، بحيث P(L_p≤μ≤R_p) = p، أي أن احتمال وقوع قيمة المتوسط المقاسة داخل الفترة يساوي p.

يتجاوز نطاق مقدمتنا القصيرة مناقشة كيفية حساب هذه الفترات بالتفصيل. يمكن العثور على المزيد من التفاصيل على ويكيبيديا. باختصار، نحدد توزيع متوسط العينة المحسوب بالنسبة إلى المتوسط الحقيقي للسكان، والذي يُطلق عليه توزيع الطالب.

معلومة مثيرة للاهتمام: تم تسمية توزيع الطالب نسبة إلى عالم الرياضيات ويليام سيلي جوسيت، الذي نشر ورقته تحت اسم مستعار "Student". كان يعمل في مصنع جينيس للبيرة، ووفقًا لإحدى الروايات، لم يرغب صاحب العمل في أن يعرف الجمهور العام أنهم يستخدمون الاختبارات الإحصائية لتحديد جودة المواد الخام.

إذا أردنا تقدير المتوسط μ للسكان بمستوى ثقة p، نحتاج إلى أخذ (1-p)/2-th percentile من توزيع الطالب A، والذي يمكن أخذه إما من الجداول أو حسابه باستخدام بعض الوظائف المدمجة في برامج الإحصاء (مثل Python، R، إلخ). ثم تكون الفترة لـ μ معطاة بـ X±A*D/√n، حيث X هو المتوسط المحصل عليه للعينة، وD هو الانحراف المعياري.

ملاحظة: نتجنب أيضًا مناقشة مفهوم مهم وهو درجات الحرية، وهو مهم فيما يتعلق بتوزيع الطالب. يمكنك الرجوع إلى كتب أكثر شمولية في الإحصاء لفهم هذا المفهوم بشكل أعمق.

تم تقديم مثال لحساب فترة الثقة للأوزان والأطوال في دفتر الملاحظات المرافق.

p	متوسط الوزن
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

لاحظ أنه كلما زادت احتمالية الثقة، زادت عرض فترة الثقة.

اختبار الفرضيات

في مجموعة بيانات لاعبي البيسبول، هناك أدوار مختلفة للاعبين، يمكن تلخيصها أدناه (انظر دفتر الملاحظات المرافق لمعرفة كيفية حساب هذا الجدول):

الدور	الطول	الوزن	العدد
الماسك	72.723684	204.328947	76
الضارب المعين	74.222222	220.888889	18
القاعدة الأولى	74.000000	213.109091	55
اللاعب الخارجي	73.010309	199.113402	194
الرامي الاحتياطي	74.374603	203.517460	315
القاعدة الثانية	71.362069	184.344828	58
اللاعب القصير	71.903846	182.923077	52
الرامي الأساسي	74.719457	205.163636	221
القاعدة الثالثة	73.044444	200.955556	45

يمكننا ملاحظة أن متوسط أطوال لاعبي القاعدة الأولى أعلى من لاعبي القاعدة الثانية. وبالتالي، قد نميل إلى استنتاج أن لاعبي القاعدة الأولى أطول من لاعبي القاعدة الثانية.

يُطلق على هذا البيان اسم فرضية، لأننا لا نعرف ما إذا كانت الحقيقة صحيحة أم لا.

ومع ذلك، ليس من الواضح دائمًا ما إذا كان يمكننا التوصل إلى هذا الاستنتاج. من المناقشة أعلاه نعلم أن لكل متوسط فترة ثقة مرتبطة، وبالتالي قد يكون هذا الاختلاف مجرد خطأ إحصائي. نحتاج إلى طريقة أكثر رسمية لاختبار فرضيتنا.

دعونا نحسب فترات الثقة بشكل منفصل لأطوال لاعبي القاعدة الأولى والثانية:

الثقة	لاعبو القاعدة الأولى	لاعبو القاعدة الثانية
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

يمكننا أن نرى أنه تحت أي مستوى ثقة لا تتداخل الفترات. وهذا يثبت فرضيتنا أن لاعبي القاعدة الأولى أطول من لاعبي القاعدة الثانية.

بشكل أكثر رسمية، المشكلة التي نحاول حلها هي معرفة ما إذا كانت توزيعين احتماليين متطابقين، أو على الأقل لهما نفس المعلمات. اعتمادًا على التوزيع، نحتاج إلى استخدام اختبارات مختلفة لذلك. إذا كنا نعلم أن توزيعاتنا طبيعية، يمكننا تطبيق اختبار الطالب t.

في اختبار الطالب t، نحسب ما يسمى قيمة t، التي تشير إلى الفرق بين المتوسطات، مع الأخذ في الاعتبار التباين. يتم إثبات أن قيمة t تتبع توزيع الطالب، مما يسمح لنا بالحصول على قيمة الحد لمستوى الثقة p (يمكن حساب ذلك أو العثور عليه في الجداول العددية). ثم نقارن قيمة t بهذه القيمة الحدية لقبول أو رفض الفرضية.

في Python، يمكننا استخدام حزمة SciPy، التي تتضمن وظيفة ttest_ind (بالإضافة إلى العديد من الوظائف الإحصائية المفيدة الأخرى!). تقوم هذه الوظيفة بحساب قيمة t لنا، كما تقوم أيضًا بالبحث العكسي لقيمة الثقة p، بحيث يمكننا فقط النظر إلى الثقة لاستخلاص الاستنتاج.

على سبيل المثال، مقارنة أطوال لاعبي القاعدة الأولى والثانية تعطينا النتائج التالية:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

في حالتنا، قيمة p منخفضة جدًا، مما يعني أن هناك دليل قوي يدعم أن لاعبي القاعدة الأولى أطول.

هناك أيضًا أنواع أخرى من الفرضيات التي قد نرغب في اختبارها، على سبيل المثال:

إثبات أن عينة معينة تتبع توزيعًا معينًا. في حالتنا افترضنا أن الأطوال موزعة بشكل طبيعي، ولكن ذلك يحتاج إلى تحقق إحصائي رسمي.
إثبات أن قيمة متوسط العينة تتوافق مع قيمة محددة مسبقًا.
مقارنة متوسطات عدد من العينات (مثل الفرق في مستويات السعادة بين الفئات العمرية المختلفة).

قانون الأعداد الكبيرة ونظرية الحد المركزي

أحد الأسباب التي تجعل التوزيع الطبيعي مهمًا هو ما يسمى نظرية الحد المركزي. لنفترض أن لدينا عينة كبيرة من قيم مستقلة N X₁, ..., X_N، مأخوذة من أي توزيع بمتوسط μ وتباين σ². ثم، بالنسبة لـ N كبيرة بما فيه الكفاية (بعبارة أخرى، عندما N→∞)، سيكون المتوسط Σ_iX_i موزعًا بشكل طبيعي، بمتوسط μ وتباين σ²/N.

طريقة أخرى لتفسير نظرية الحد المركزي هي القول إنه بغض النظر عن التوزيع، عندما تحسب متوسط مجموع أي قيم متغير عشوائي، ينتهي بك الأمر بتوزيع طبيعي.

من نظرية الحد المركزي يتبع أيضًا أنه، عندما N→∞، يصبح احتمال أن يكون متوسط العينة مساويًا لـ μ يساوي 1. وهذا يُعرف بـ قانون الأعداد الكبيرة.

التغاير والارتباط

أحد الأشياء التي يقوم بها علم البيانات هو إيجاد العلاقات بين البيانات. نقول إن سلسلتين تتوافقان عندما تظهران سلوكًا مشابهًا في نفس الوقت، أي ترتفعان/تنخفضان معًا، أو ترتفع واحدة عندما تنخفض الأخرى والعكس صحيح. بمعنى آخر، يبدو أن هناك علاقة بين سلسلتين.

الارتباط لا يشير بالضرورة إلى علاقة سببية بين سلسلتين؛ أحيانًا يمكن أن تعتمد كلا المتغيرين على سبب خارجي، أو يمكن أن يكون مجرد صدفة أن السلسلتين تتوافقان. ومع ذلك، فإن الارتباط الرياضي القوي هو مؤشر جيد على أن المتغيرين مرتبطان بطريقة ما.

رياضيًا، المفهوم الرئيسي الذي يظهر العلاقة بين متغيرين عشوائيين هو التغاير، الذي يُحسب كالتالي: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. نحسب الانحراف لكلا المتغيرين عن قيم المتوسط الخاصة بهما، ثم حاصل ضرب تلك الانحرافات. إذا انحرف كلا المتغيرين معًا، سيكون حاصل الضرب دائمًا قيمة إيجابية، مما يضيف إلى تغاير إيجابي. إذا انحرف كلا المتغيرين بشكل غير متزامن (أي ينخفض أحدهما عن المتوسط عندما يرتفع الآخر فوق المتوسط)، سنحصل دائمًا على أرقام سلبية، مما يضيف إلى تغاير سلبي. إذا كانت الانحرافات غير مرتبطة، ستضيف إلى ما يقرب من الصفر.

القيمة المطلقة للتغاير لا تخبرنا كثيرًا عن مدى قوة الارتباط، لأنها تعتمد على حجم القيم الفعلية. لتطبيعها، يمكننا تقسيم التغاير على الانحراف المعياري لكلا المتغيرين للحصول على الارتباط. الشيء الجيد هو أن الارتباط دائمًا في النطاق [-1,1]، حيث يشير 1 إلى ارتباط إيجابي قوي بين القيم، و-1 إلى ارتباط سلبي قوي، و0 إلى عدم وجود ارتباط على الإطلاق (المتغيرات مستقلة).

مثال: يمكننا حساب الارتباط بين الأوزان والأطوال للاعبي البيسبول من مجموعة البيانات المذكورة أعلاه:

print(np.corrcoef(weights,heights))

كنتيجة، نحصل على مصفوفة الارتباط مثل هذه:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

يمكن حساب مصفوفة الارتباط C لأي عدد من السلاسل المدخلة S₁, ..., S_n. قيمة C_ij هي الارتباط بين S_i وS_j، والعناصر القطرية دائمًا 1 (وهو أيضًا الارتباط الذاتي لـ S_i).

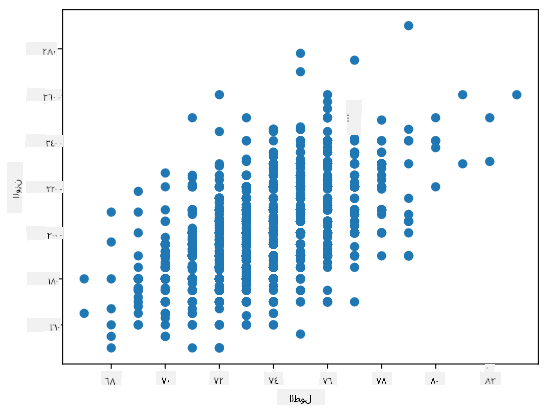
في حالتنا، تشير القيمة 0.53 إلى وجود بعض الارتباط بين وزن وطول الشخص. يمكننا أيضًا إنشاء مخطط انتشار لقيمة مقابل الأخرى لرؤية العلاقة بصريًا:

يمكن العثور على المزيد من أمثلة الارتباط والتغاير في دفتر الملاحظات المرافق.

الخاتمة

في هذا القسم، تعلمنا:

الخصائص الإحصائية الأساسية للبيانات، مثل المتوسط، التباين، النمط والرباعيات
توزيعات مختلفة للمتغيرات العشوائية، بما في ذلك التوزيع الطبيعي
كيفية إيجاد الارتباط بين الخصائص المختلفة
كيفية استخدام الأدوات الرياضية والإحصائية لإثبات بعض الفرضيات
كيفية حساب فترات الثقة للمتغير العشوائي بناءً على عينة البيانات

بينما هذه ليست قائمة شاملة للمواضيع الموجودة ضمن الاحتمالات والإحصاء، يجب أن تكون كافية لتمنحك بداية جيدة في هذه الدورة.

🚀 التحدي

استخدم الكود النموذجي في دفتر الملاحظات لاختبار فرضيات أخرى مثل:

لاعبو القاعدة الأولى أكبر سنًا من لاعبي القاعدة الثانية
لاعبو القاعدة الأولى أطول من لاعبي القاعدة الثالثة
اللاعبون القصيرون أطول من لاعبي القاعدة الثانية

اختبار ما بعد المحاضرة

المراجعة والدراسة الذاتية

الاحتمالات والإحصاء موضوع واسع يستحق دورة خاصة به. إذا كنت مهتمًا بالتعمق في النظرية، قد ترغب في متابعة قراءة بعض الكتب التالية:

كارلوس فرنانديز-جراندا من جامعة نيويورك لديه ملاحظات محاضرة رائعة الاحتمالات والإحصاء لعلم البيانات (متاحة عبر الإنترنت)
بيتر وأندرو بروس. الإحصاء العملي لعلماء البيانات. [كود نموذجي في R].
جيمس دي ميلر. الإحصاء لعلم البيانات [كود نموذجي في R]

الواجب

دراسة صغيرة عن مرض السكري

الشكر

تم تأليف هذا الدرس بحب ♥️ بواسطة ديمتري سوشنيكوف

إخلاء المسؤولية:
تمت ترجمة هذا المستند باستخدام خدمة الترجمة الآلية Co-op Translator. بينما نسعى لتحقيق الدقة، يرجى العلم أن الترجمات الآلية قد تحتوي على أخطاء أو عدم دقة. يجب اعتبار المستند الأصلي بلغته الأصلية هو المصدر الموثوق. للحصول على معلومات حساسة أو هامة، يُوصى بالاستعانة بترجمة بشرية احترافية. نحن غير مسؤولين عن أي سوء فهم أو تفسيرات خاطئة تنشأ عن استخدام هذه الترجمة.

32 KiB Raw Permalink Blame History Unescape Escape