15 KiB
Construindo um modelo de regressão usando Scikit-learn: regressão em dois modos
Infográfico por Dasani Madipalli
Questionário inicial
Esta liçao está disponível em R!
Introdução
Até agora, você viu o que é regressão com dados de amostra coletados do conjunto de dados de preços de abóboras, usaremos esse conjunto de dados ao longo desta lição. Você também o visualizou usando Matplotlib.
Você está pronto para mergulhar mais fundo na regressão para ML. Nesta lição, você aprenderá mais sobre dois tipos de regressão: regressão linear básica e regressão polinomial, junto com um pouco da matemática que fundamenta essas duas técnicas.
Ao longo deste curso, assumimos um conhecimento mínimo de matemática e procuramos torná-lo acessível para alunos vindos de outras áreas, portanto, preste atenção às notas, 🧮 legendas, diagramas e outras ferramentas de aprendizagem para ajudar na compreensão.
Pré-requisito
Você já deve saber mais ou menos como é a estrutura do conjunto de dados de abóboras que estávamos examinando. Você pode encontrá-lo já tratado no arquivo notebook.ipynb desta lição. No arquivo, o preço da abóbora é exibido por bushel (aquela unidade de medida 😅) em um novo dataframe. Certifique-se de que você pode executar os notebooks no Visual Studio Code.
Preparação
Lembre-se de que você está carregando esses dados para produzir questionamentos a partir deles.
- Qual é a melhor época para comprar abóboras?
- Que preço posso esperar de uma caixa de abóboras pequenas?
- Devo comprar abóboras em caixas de 1/2 bushel ou de 1 1/9?
Vamos continuar investigando esses dados.
Na lição anterior, você criou um dataframe Pandas e o preencheu com parte do conjunto de dados original, padronizando o preço por bushel. Porém, ao fazer isso só foi possível reunir cerca de 400 pontos de dados e apenas para os meses de outono.
Dê uma olhada nos dados que pré-carregamos no notebook que acompanha esta lição. Os dados são pré-carregados e um gráfico de dispersão inicial é traçado para mostrar os dados do mês. Talvez possamos obter mais detalhes sobre a natureza dos dados fazendo uma limpeza.
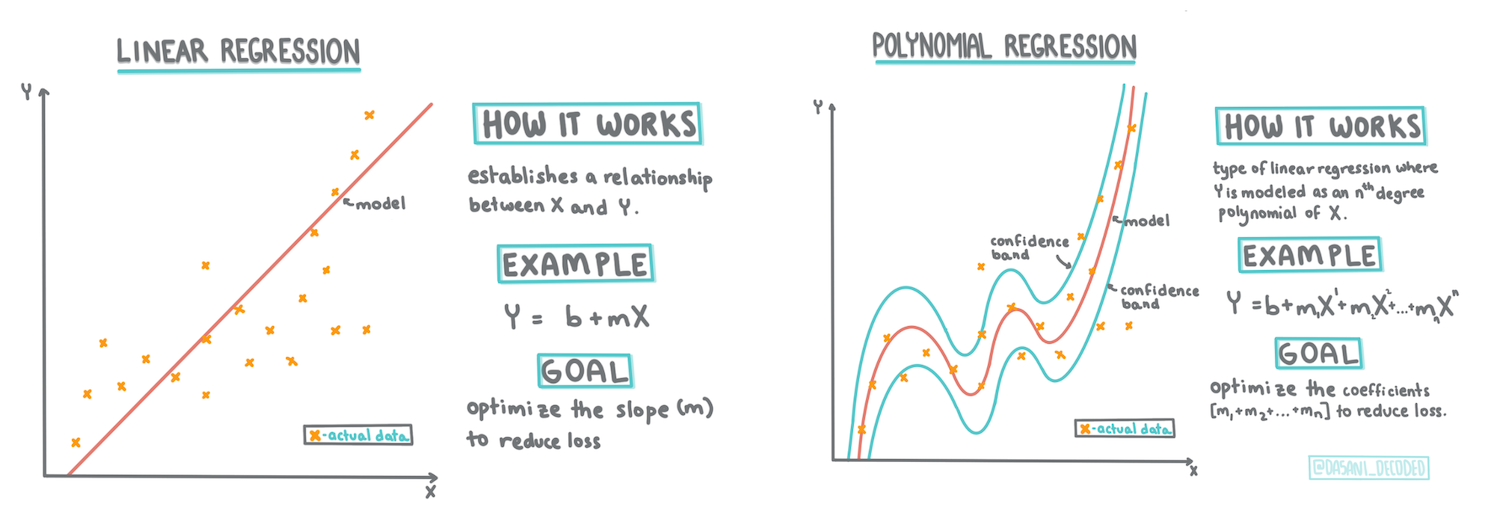
Linha de regressão linear
Como você aprendeu na Lição 1, o objetivo de um exercício de regressão linear é ser capaz de traçar uma linha para:
- Mostrar relações entre variáveis.
- Fazer previsões. Previsões sobre onde um novo ponto de dados ficaria em relação a linha.
É típico da Regressão de Mínimos Quadrados traçar esse tipo de linha. O termo 'mínimos quadrados' significa que todos os pontos de dados ao redor da linha de regressão são quadrados e somados. Idealmente, essa soma final é a menor possível, porque queremos um baixo número de erros, ou mínimos quadrados.
Fazemos isso porque queremos modelar uma linha que tenha a menor distância cumulativa de todos os nossos pontos de dados. Também elevamos os termos ao quadrado antes de adicioná-los, pois estamos preocupados com sua magnitude e não com sua direção.
🧮 Me mostre a matemática
Esta linha, chamada de linha de melhor ajuste, pode ser expressa por uma equação:
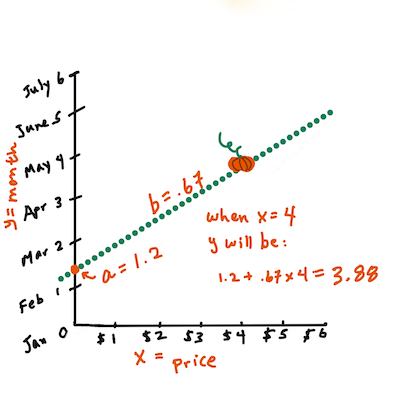
Y = a + bX
Xé a 'variável explanatória'.Yé a 'variável dependente'.bé a inclinação da linha eaé a interseção de y, que se refere ao valor deYquandoX = 0.Primeiro, calculamos a inclinação
b(Infográfico por Jen Looper).Em outras palavras, e se referindo à pergunta original sobre os dados das abóboras: "prever o preço mensal de uma abóbora por bushel",
Xseria o preço eYo mês de venda.Agora calcule o valor de
Y. Se você está pagando cerca de US $ 4, então deve ser abril! (Infográfico por Jen Looper).Esse cálculo deve demonstrar a inclinação da linha, que também depende da interseção, ou onde
Yestá situado quandoX = 0.Você pode observar o cálculo desses valores no site Math is Fun (Matemática é divertida). Visite também esta calculadora de mínimos quadrados para observar como os valores dos números afetam a linha.
Correlação
Mais um termo a ser entendido é o Coeficiente de correlação entre as variáveis X e Y fornecidas. Usando um gráfico de dispersão, você pode visualizar rapidamente esse coeficiente. Um gráfico com pontos de dados espalhados quase no mesmo formato da linha tem alta correlação, mas um gráfico com pontos de dados espalhados por toda parte entre X e Y tem uma correlação baixa.
Um bom modelo de regressão linear será aquele que tiver um coeficiente de correlação alto (mais próximo de 1 do que 0) usando o método de regressão por mínimos quadrados com uma linha de regressão.
✅Execute o notebook desta lição e observe o gráfico de dispersão usando as colunas City (cidade) e Price (preço). Os dados que associam a cidade ao preço para vendas de abóboras parecem ter alta ou baixa correlação?
Prepare seus dados para regressão
Usando a matemática por trás deste exercício, crie um modelo de regressão para prever qual melhor preço de caixa de abóbora. Um comprador de abóbora vai querer saber desse tipo de informação para otimizar suas compras.
Como você usará o Scikit-learn, não há razão para fazer isso manualmente (mas você pode!). No bloco principal do seu notebook, adicione a biblioteca do Scikit-learn para converter automaticamente todos os dados string em números:
from sklearn.preprocessing import LabelEncoder
new_pumpkins.iloc[:, 0:-1] = new_pumpkins.iloc[:, 0:-1].apply(LabelEncoder().fit_transform)
Se você olhar para o dataframe new_pumpkins agora, verá que todas as strings são números. Isso torna a leitura mais difícil, mas muito mais simples para o Scikit-learn!
Você pode tomar decisões robustas (não apenas com base em um gráfico de dispersão) sobre os melhores dados para a regressão.
Tente encontrar uma boa correlação entre dois pontos de seus dados para construir um bom modelo preditivo. Vemos que há uma correlação baixa entre City e Price:
print(new_pumpkins['City'].corr(new_pumpkins['Price']))
0.32363971816089226
Porém, há uma correlação um pouco melhor entre Package (pacote) e Price. Isso faz sentido, né? Normalmente, quanto maior a caixa de produtos, mais alto é o preço.
print(new_pumpkins['Package'].corr(new_pumpkins['Price']))
0.6061712937226021
Uma boa pergunta sobre esses dados seria: 'Que preço posso esperar de uma determinada caixa de abóbora?'.
Vamos construir o modelo de regressão.
Construindo um modelo linear
Antes de construir seu modelo, vamos tratar os dados mais uma vez. Elimine quaisquer dados nulos e verifique os dados mais uma vez.
new_pumpkins.dropna(inplace=True)
new_pumpkins.info()
Em seguida, crie um novo dataframe a partir desse conjunto e imprima-o:
new_columns = ['Package', 'Price']
lin_pumpkins = new_pumpkins.drop([c for c in new_pumpkins.columns if c not in new_columns], axis='columns')
lin_pumpkins
Package Price
70 0 13.636364
71 0 16.363636
72 0 16.363636
73 0 15.454545
74 0 13.636364
... ... ...
1738 2 30.000000
1739 2 28.750000
1740 2 25.750000
1741 2 24.000000
1742 2 24.000000
415 rows × 2 columns
-
Atribua seu X e y:
X = lin_pumpkins.values[:, :1] y = lin_pumpkins.values[:, 1:2]
✅ Mas o que é isso? Você está usando a notação slice para criar arrays e populá-los nas variáveis X and y.
-
Comece as rotinas de construção do modelo de regressão:
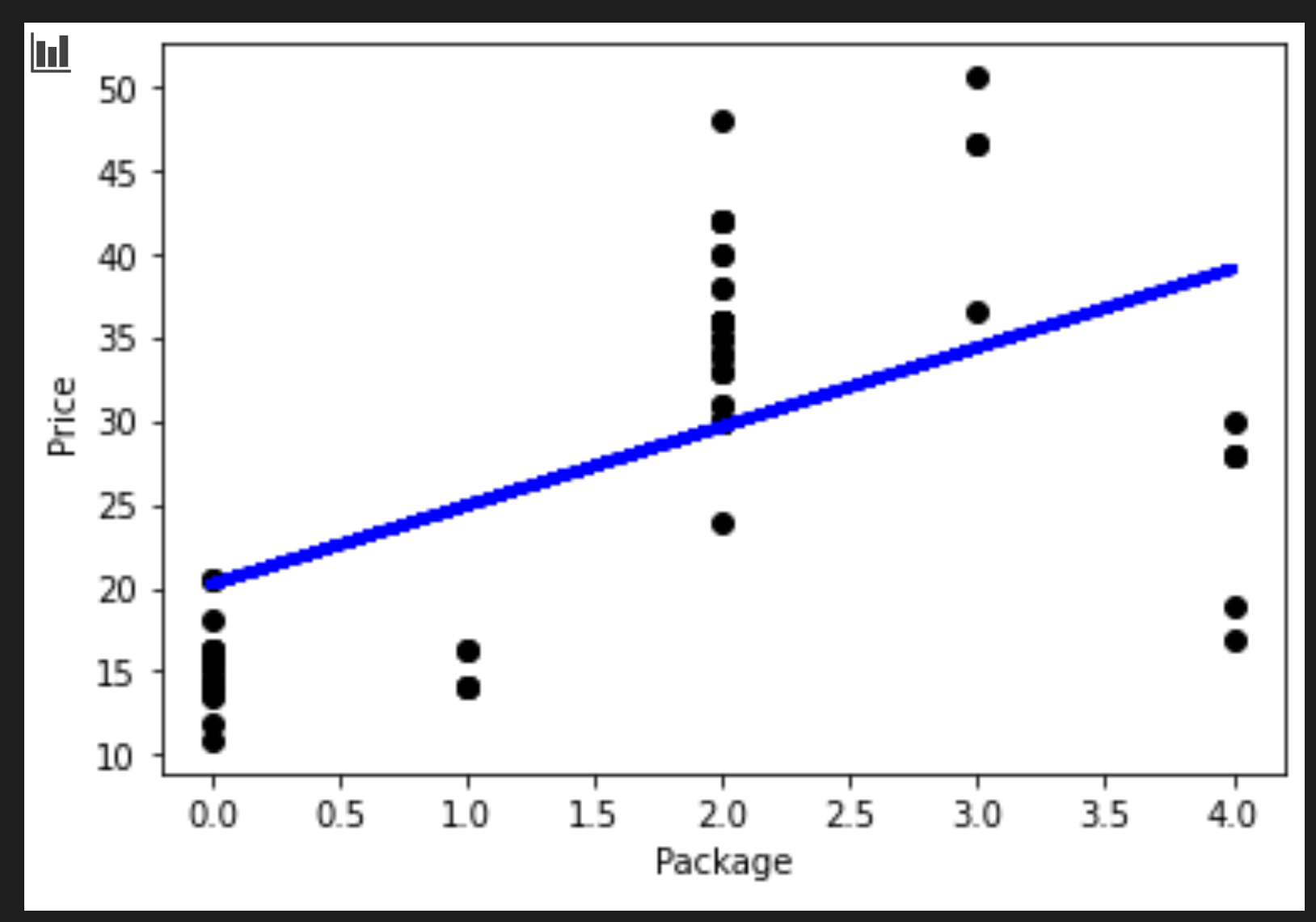
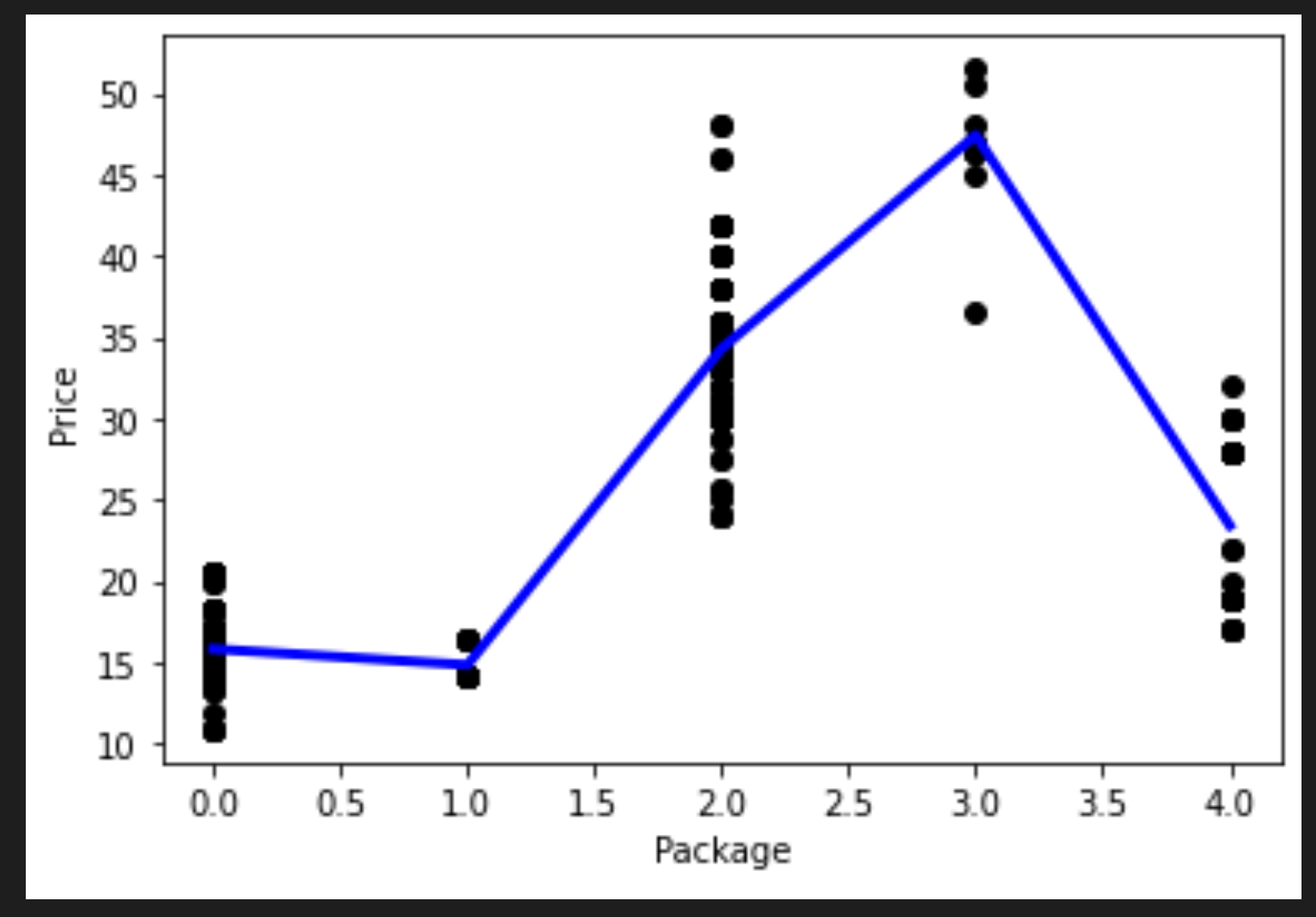
from sklearn.linear_model import LinearRegression from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) pred = lin_reg.predict(X_test) accuracy_score = lin_reg.score(X_train,y_train) print('Model Accuracy: ', accuracy_score)Como a correlação não é tão boa, o modelo não é muito preciso.
Model Accuracy: 0.3315342327998987 -
Para visualizar a linha, use o código abaixo:
plt.scatter(X_test, y_test, color='black') plt.plot(X_test, pred, color='blue', linewidth=3) plt.xlabel('Package') plt.ylabel('Price') plt.show() -
Teste o modelo com um valor hipotético de variedade (coluna Variety):
lin_reg.predict( np.array([ [2.75] ]) )O preço devolvido é:
array([[33.15655975]])
O número faz sentido se a lógica da linha de regressão estiver correta.
🎃 Parabéns, você acabou de criar um modelo que pode ajudar a prever o preço de uma caixa (ou outro tipo de medida) de abóboras. Já vai ter decoração de halloween até o do ano que vem ou já pode aprimorar seu histórico de receitas que levam abóbora.
Lembre-se que sempre tem como melhorar o seu modelo!
Regressão polinomial
Outro tipo de regressão linear é a regressão polinomial. Embora às vezes haja uma relação linear entre as variáveis - quanto maior o volume da abóbora, mais alto é o preço -, às vezes essas relações não podem ser representadas como um plano ou uma linha reta.
✅ Aqui estão mais exemplos de dados que podem usar regressão polinomial.
Dê uma outra olhada na relação entre Variety e Price no gráfico anterior. Este gráfico de dispersão parece que deve ser analisado por uma linha reta? Talvez não. Nesse caso, você pode tentar a regressão polinomial.
✅ Polinômios são expressões matemáticas que podem consistir em uma ou mais variáveis e coeficientes.
A regressão polinomial cria uma linha curva para ajustar melhor os dados não lineares.
-
Vamos recriar um dataframe preenchido com um segmento dos dados originais:
new_columns = ['Variety', 'Package', 'City', 'Month', 'Price'] poly_pumpkins = new_pumpkins.drop([c for c in new_pumpkins.columns if c not in new_columns], axis='columns') poly_pumpkins
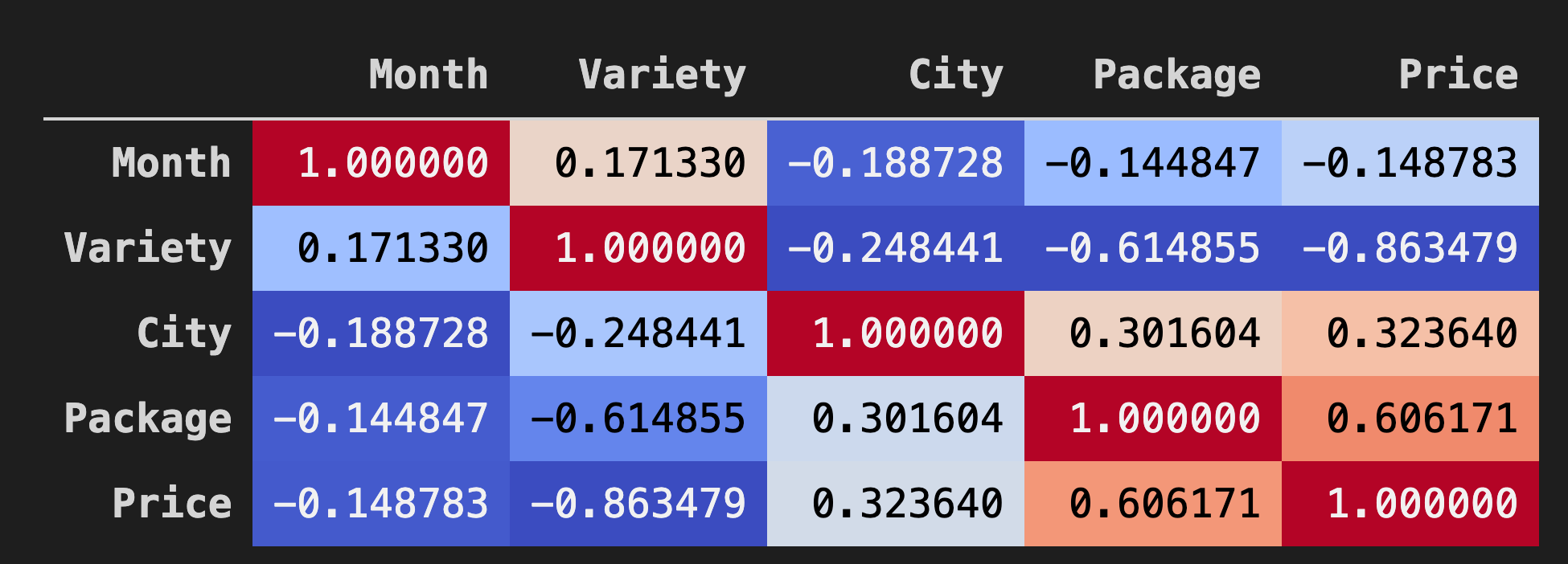
Uma boa forma de visualizar as correlações entre os dados em dataframes é exibi-los em um gráfico 'coolwarm':
-
Use o método
Background_gradient()comcoolwarmcomo parâmetro:corr = poly_pumpkins.corr() corr.style.background_gradient(cmap='coolwarm')Este código cria um mapa de calor:
Este gráfico mostra a boa correlação entre Package e Price. Portanto, você pode criar um modelo melhor que o anterior.
Criando um pipeline
Scikit-learn inclui uma API para construir modelos de regressão polinomial - a API make_pipeline. É criado um pipeline que consiste em uma cadeia de estimadores. Nesse caso, o pipeline inclui recursos polinomiais ou previsões que formam um caminho não linear.
-
Populamos X e y:
X=poly_pumpkins.iloc[:,3:4].values y=poly_pumpkins.iloc[:,4:5].values -
Criamos um pipeline chamando a função
make_pipeline():from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(4), LinearRegression()) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) pipeline.fit(np.array(X_train), y_train) y_pred=pipeline.predict(X_test)
Criando uma sequência
Neste momento, você precisa criar um novo dataframe com dados classificados para que o pipeline possa criar uma sequência.
Adicione o código abaixo:
df = pd.DataFrame({'x': X_test[:,0], 'y': y_pred[:,0]})
df.sort_values(by='x',inplace = True)
points = pd.DataFrame(df).to_numpy()
plt.plot(points[:, 0], points[:, 1],color="blue", linewidth=3)
plt.xlabel('Package')
plt.ylabel('Price')
plt.scatter(X,y, color="black")
plt.show()
Você criou um novo dataframe chamando pd.DataFrame. Em seguida, classificou os valores chamando sort_values(). Finalmente, você criou um gráfico polinomial:
Você pode ver uma linha curva que se ajusta melhor aos seus dados.
Vamos verificar a acurácia do modelo:
accuracy_score = pipeline.score(X_train,y_train)
print('Model Accuracy: ', accuracy_score)
Tcharam! ✨
Model Accuracy: 0.8537946517073784
Fazendo previsões
Podemos inserir um novo valor e obter uma previsão?
Chame predict() para pedir uma previsão:
pipeline.predict( np.array([ [2.75] ]) )
E conseguimos:
array([[46.34509342]])
Agora faz sentido! E se esse modelo for melhor que o anterior usando o mesmo conjunto de dados, você já pode fazer orçamentos para abóboras mais caras! 😂
🏆 Muito bem! Você criou dois modelos de regressão em uma lição. Na lição final, você aprenderá sobre regressão logística para determinar categorias 🤩.
🚀Desafio
Teste variáveis diferentes neste notebook para ver como a correlação corresponde à acurácia do modelo.
Questionário para fixação
Revisão e Auto Aprendizagem
Nesta lição, aprendemos sobre regressão linear. Existem outros tipos importantes de regressão. Leia sobre as técnicas Stepwise, Ridge, Lasso e Elasticnet. Um bom curso para um estudo mais aprofundado é o Stanford Statistical Learning course (Curso de aprendizagem estatística de Stanford).