19 KiB
CartPole 스케이팅
이전 강의에서 풀었던 문제는 장난감 문제처럼 보일 수 있고, 실제 시나리오에서 진짜 적용되지 않습니다. 체스나 바둑을 즐기는 것을 포함한 - 시나리오에 많은 실제 문제와 공유하기 때문에, 이 케이스는 아닙니다. 주어진 룰과 discrete state를 보드가 가지고 있기 때문에 비슷합니다.
강의 전 퀴즈
소개
이 강의에서 Q-Learning의 같은 원칙을 하나 이상의 실수가 주어진 state인, continuous state 문제로 적용할 예정입니다. 다음 문제를 다루게 됩니다:
문제: 만약 Peter가 늑대로부터 도망가길 원한다면, 빠르게 움직일 필요가 있습니다. Peter가 특히 Q-Learning으로, 밸런스를 유지하면서, 스케이트를 배울 수 있는지 보게 됩니다.
Peter와 친구들은 늑대로부터 도망갈 창의력을 얻습니다! Image by Jen Looper
CartPole 문제로 알려진 밸런스있는 간단한 버전을 사용할 예정입니다. cartpole 월드에서, 왼쪽과 오른쪽으로 움직일 수 있는 수평 슬라이더를 가지며, 목표는 슬라이더의 위쪽에 있는 수직 폴을 밸런스하는 것입니다.
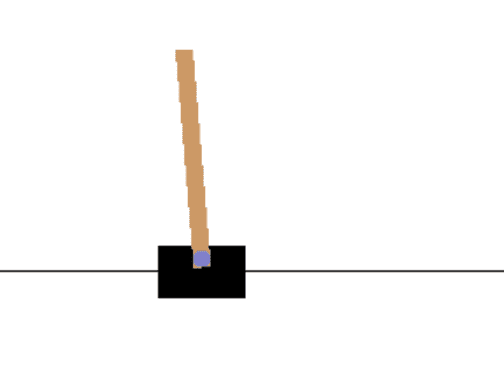
전제 조건
이 강의에서, OpenAI Gym으로 불리는 라이브러리를 사용해서 다른 environments를 시뮬레이션합니다. 이 강의의 코드를 로컬에서 (에시. from Visual Studio Code), 새로운 윈도우로 열어서 시뮬레이션할 수 있습니다. 코드를 온라인으로 실행할 때는, here에서 설명된 것처럼, 코드를 약간 트윅할 필요가 있습니다.
OpenAI Gym
이전 강의에서, 게임의 룰과 state는 스스로 정의했던 Board 클래스로 주어졌습니다. balancing pole의 물리학 그늘에서 시뮬레이션하는, 특별한 simulation environment를 사용할 예정입니다. 가장 인기있는 reinforcement learning 알고리즘을 훈련하기 위한 시뮬레이션 환경은 OpenAI애서 관리하는, Gym이라고 불립니다. 이 gym을 사용해서 cartpole 시뮬레이션부터 Atari 게임까지 다양한 environments를 만들 수 있습니다.
노트: OpenAI Gym here에서 사용할 수 있는 다양한 환경을 볼 수 있습니다.
먼저, gym을 설치하고 필요한 라이브러리를 가져옵니다 (code block 1):
import sys
!{sys.executable} -m pip install gym
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
연습 - cartpole 환경 초기화
cartpole balancing 문제를 풀려면, 대상 환경을 초기화할 필요가 있습니다.각 환경은 이렇게 연결되었습니다:
-
Observation space 은 환경으로부터 받는 정보의 구조를 정의합니다. cartpole 문제라면, 폴의 위치, 속도와 일부 기타 값을 받습니다.
-
Action space 는 가능한 액션을 정의합니다. 이 케이스에서 action space는 추상적이고, 두 액션 left와 right로 이루어져 있습니다. (code block 2)
-
초기화하려면, 다음 코드를 타이핑합니다:
env = gym.make("CartPole-v1") print(env.action_space) print(env.observation_space) print(env.action_space.sample())
어떻게 환경이 동작하는지 보려면, 100 번 짧게 시뮬레이션 돌립니다. 각 단계에서, 수행할 액션 중 하나를 제공합니다 - 이 시뮬레이션에서 action_space로 액션을 랜덤 선택하게 됩니다.
-
아래 코드를 실행하고 어떤 결과가 나오는지 봅니다.
✅ 로컬 설치한 Python에서 이 코드를 실행하도록 권장한다는 점을 기억합니다! (code block 3)
env.reset() for i in range(100): env.render() env.step(env.action_space.sample()) env.close()이 이미지와 비슷한 내용이 보여지게 됩니다:
-
시뮬레이션하는 동안, 액션 방식을 판단하기 위해서 관찰할 필요가 있습니다. 사실, step 함수는 현재 관측치, 보상 함수, 그리고 시뮬레이션을 지속하거나 끝내고자 가리키는 종료 플래그를 반환합니다: (code block 4)
env.reset() done = False while not done: env.render() obs, rew, done, info = env.step(env.action_space.sample()) print(f"{obs} -> {rew}") env.close()노트북 출력에서 이렇게 보이게 됩니다:
[ 0.03403272 -0.24301182 0.02669811 0.2895829 ] -> 1.0 [ 0.02917248 -0.04828055 0.03248977 0.00543839] -> 1.0 [ 0.02820687 0.14636075 0.03259854 -0.27681916] -> 1.0 [ 0.03113408 0.34100283 0.02706215 -0.55904489] -> 1.0 [ 0.03795414 0.53573468 0.01588125 -0.84308041] -> 1.0 ... [ 0.17299878 0.15868546 -0.20754175 -0.55975453] -> 1.0 [ 0.17617249 0.35602306 -0.21873684 -0.90998894] -> 1.0시뮬레이션의 각 단계에서 반환되는 관찰 백터는 다음 값을 포함합니다:
- Position of cart
- Velocity of cart
- Angle of pole
- Rotation rate of pole
-
이 숫자의 최소 최대 값을 가져옵니다: (code block 5)
print(env.observation_space.low) print(env.observation_space.high)각 시뮬레이션 단계의 보상 값은 항상 1이라는 점을 알 수 있습니다. 목표는 가장 긴 기간에 폴을 합리적으로 수직 위치에 유지하며, 가능한 오래 생존하는 것입니다.
✅ 사실, the CartPole 시뮬레이션은 100번 넘는 시도에서 평균 195개 보상을 얻을 수 있게 관리되면 해결된 것으로 여깁니다.
State discretization
Q-Learning에서, 각 state에서 할 것을 정의하는 Q-Table을 만들 필요가 있습니다. 이렇게 하려면, state가 discreet으로 되어야하고, 더 정확해지면, 한정된 discrete 값 숫자를 포함해야 합니다. 그래서, 관측치를 어떻게든지 discretize 해서, 한정된 state 세트와 맵핑할 필요가 있습니다.
이렇게 할 수 있는 몇 방식이 있습니다:
- Divide into bins. 만약 특정 값의 간격을 알고있다면, 간격을 bins의 수로 나누고, 값을 속해있는 bin 숫자로 변환할 수 있습니다. numpy
digitize메소드로 마무리 지을 수 있습니다. 이 케이스에서, 디지털화를 선택하기 위해서 bin의 수를 기반했기 때문에, state 크기를 정확히 알게 됩니다.
✅ linear interpolation으로 값을 한정된 간격 (say, from -20 to 20)에 가져오고, 반올림해서 숫자를 정수로 변환할 수 있습니다. 특별하게 입력 값의 정확한 범위를 모른다면, state의 크기에서 조금만 컨트롤하게 둡니다. 예시로, 4개 중에 2개 값은 상/하 한도가 없으므로, state 개수에서 무한으로 결과가 나올 수 있습니다.
예시에서, 두 번째 접근 방식을 사용하겠습니다. 나중에 알게 되듯이, 정의하지 못한 상/하 한도에도, 이 값은 특정하게 한정된 간격에 벗어난 값을 드물게 가지므로, 극단적인 값을 가진 state는 매우 드뭅니다.
-
여기는 모델에서 관측치를 가지고, 4개 정수 값의 튜플을 만드는 함수입니다: (code block 6)
def discretize(x): return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int)) -
bin으로 다른 discretization 방식도 찾아봅니다: (code block 7)
def create_bins(i,num): return np.arange(num+1)*(i[1]-i[0])/num+i[0] print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10)) ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter nbins = [20,20,10,10] # number of bins for each parameter bins = [create_bins(ints[i],nbins[i]) for i in range(4)] def discretize_bins(x): return tuple(np.digitize(x[i],bins[i]) for i in range(4)) -
지금부터 짧은 시뮬레이션을 실행하고 분리된 환경 값을 관찰합니다. 자유롭게
discretize와discretize_bins를 시도하고 다른점이 있다면 봅시다.✅ discretize_bins는 0-베이스인, bin 숫자를 반환합니다. 그래서 0 주변 입력 변수의 값은 간격의 중간에서 (10) 숫자를 반환합니다. discretize에서, 출력 값의 범위에 대해서 신경쓰지 못하고, negative를 허용하므로, state 값은 바뀌지 못하고, 0은 0에 대응합니다. (code block 8)
env.reset() done = False while not done: #env.render() obs, rew, done, info = env.step(env.action_space.sample()) #print(discretize_bins(obs)) print(discretize(obs)) env.close()✅ 만약 환경 실행이 어떻게 되는지 보려면 env.render로 시작되는 줄을 주석 해제합니다. 그렇지 않으면 빠르게, 백그라운드에서 실행할 수 있습니다. Q-Learning 프로세스가 진행되면서 "invisible" 실행으로 사용할 수 있습니다.
Q-Table 구조
이전 강의에서, state는 0부터 8까지 숫자의 간단한 쌍이라서, 8x8x2 형태 numpy tensor로 Q-Table를 표현하는 게 편리합니다. 만약 bins discretization를 사용하면, state vector의 크기를 알 수 있으므로, 같은 접근 방식을 사용하고 20x20x10x10x2 형태 배열로 state를 나타냅니다 (여기 2 개는 액션 공간의 차원이고, 첫 차원은 관찰 공간에서 각 파라미터를 사용하고자 선택된 bin의 숫자에 해당합니다).
그러나, 가끔은 관찰 공간의 정확한 넓이를 알 수 없습니다. discretize 함수의 케이스에서, 원본 값의 일부는 결합되지 않으므로, state가 특정한 제한 사항에 놓여있는지 확신할 수 없습니다. 따라서, 조금 다른 접근 방식으로 사용하고 dictionary로 Q-Table을 표현할 예정입니다.
-
dictionary 키로 (state,action) 쌍을 사용하고, 값을 Q-Table 엔트리 값에 대응합니다. (code block 9)
Q = {} actions = (0,1) def qvalues(state): return [Q.get((state,a),0) for a in actions]여기 가능한 모든 액션에 해당하는 state로 주어진 Q-Table 값의 리스트를 반환하는,
qvalues()함수도 정의합니다. 만약 앤트리가 Q-Table에 없다면, 기본적으로 0을 반환합니다.
Q-Learning 시작합시다
지금부터 Peter에게 밸런스를 가르치기 직전입니다!
-
먼저, 일부 hyperparameters를 맞춥시다: (code block 10)
# hyperparameters alpha = 0.3 gamma = 0.9 epsilon = 0.90여기,
alpha는 각 단계에서 Q-Table의 현재 값을 어느정도 범위로 조정할 수 있게 정의하는 learning rate입니다. 이전 강의에서는 1로 시작하고, 훈련하는 동안alpha를 낮은 값으로 낮춥니다. 이 예시에서 간단하게 하고자 변함없이 그대로 두고,alpha값을 조정하는 실험을 나중에 진행할 수 있습니다.gamma는 현재 보상을 넘는 미래 보상에 얼마나 우선 순위를 두어야 할지 나타내는 discount factor입니다.epsilon는 exploitation보다 exploration을 선호하는지 안 하는지에 관해 결정하는 exploration/exploitation factor입니다. 알고리즘에서,epsilon퍼센트의 케이스는 Q-Table 값에 따라서 다음 액션을 선택하고, 남는 케이스에서는 랜덤 액션을 수행할 예정입니다. 전에 본 적 없는 검색 공간의 영역을 탐색할 수 있습니다.✅ 밸런싱의 측면에서 - 랜덤 액션을 (exploration) 선택하는 것은 잘못된 방향으로 랜덤 펀치를 날릴 수 있으며, pole은 이 "실수"에서 밸런스를 복구하는 방식을 배우게 됩니다.
알고리즘 개선
이전 강의의 알고리즘을 두 번 개선할 수 있습니다:
-
여러 번 시뮬레이션해서, 평균 누적 보상을 계산합니다. 각자 5000번 반복하면서 프로세스를 출력하고, 이 시간 동안에 누적 보상을 계산합니다. 195 포인트보다 더 얻었다면 - 필수보다 더 높은 퀄리티로, 문제를 해결한 것으로 간주한다는 점을 의미합니다.
-
Qmax로, 최대 평균 누적 결과를 계산하고, 이 결과와 일치하는 Q-Table에 저장합니다. 훈련을 할 때 가끔 평균 누적 결과가 드랍되기 시작하는 것을 알아챌 수 있고, 훈련 중 관찰된 좋은 모델에 해당하는 Q-Table의 값을 그대로 두고 싶습니다.
-
plot을 진행하기 위해서
rewardsvector로 각 시뮬레이션의 누적 보상을 얻을 수 있습니다. (code block 11)def probs(v,eps=1e-4): v = v-v.min()+eps v = v/v.sum() return v Qmax = 0 cum_rewards = [] rewards = [] for epoch in range(100000): obs = env.reset() done = False cum_reward=0 # == do the simulation == while not done: s = discretize(obs) if random.random()<epsilon: # exploitation - chose the action according to Q-Table probabilities v = probs(np.array(qvalues(s))) a = random.choices(actions,weights=v)[0] else: # exploration - randomly chose the action a = np.random.randint(env.action_space.n) obs, rew, done, info = env.step(a) cum_reward+=rew ns = discretize(obs) Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns))) cum_rewards.append(cum_reward) rewards.append(cum_reward) # == Periodically print results and calculate average reward == if epoch%5000==0: print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}") if np.average(cum_rewards) > Qmax: Qmax = np.average(cum_rewards) Qbest = Q cum_rewards=[]
이 결과에서 알 수 있습니다:
-
목표에 가까워집니다. 시뮬레이션을 100+번 넘게 계속 하면 195개 누적 보상을 얻는 목표에 가까워지거나, 실제로 달성했을 수도 있습니다! 만약 작은 숫자를 얻더라도, 평균적으로 5000번 넘게 하고, 드러나있는 표준으로도 100번만 수행해도 되므로, 여전히 알 수 없습니다.
-
보상이 드랍되기 시작합니다. 가끔 보상이 드랍되기 시작하면, 시뮬레이션을 안 좋게 만들어서 Q-Table에 이미 학습한 값을 "destroy"할 수 있다는 점을 의미합니다.
이 관측치는 훈련 프로세스를 plot하면, 더 명확히 보입니다.
훈련 프로세스 Plotting
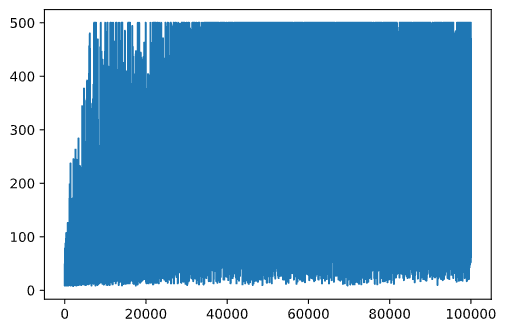
훈련 하면서, rewards vector로 각 반복에서 누적 보상 값을 얻었습니다. 여기에서 반복 숫자로 plot할 때 볼 수 았습니다:
plt.plot(rewards)
그래프에서, 추계학 훈련 프로세스의 특성으로 훈련 세션 길이가 매우 달라지므로, 모든 것을 말할 수 없습니다. 이 그래프를 잘 이해하도록, 훈련 시리즈로 running average를 계산할 수 있습니다. 100으로 합시다. np.convolve으로 편하게 마무리 지을 수 있습니다: (code block 12)
def running_average(x,window):
return np.convolve(x,np.ones(window)/window,mode='valid')
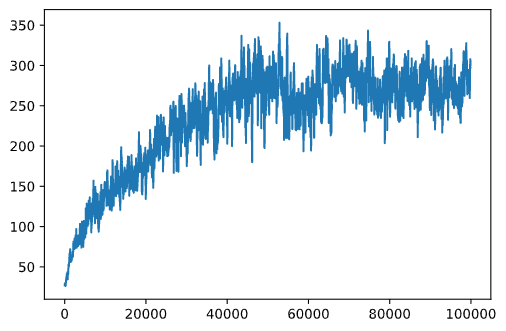
plt.plot(running_average(rewards,100))
다양한 hyperparameters
더 안정적으로 훈련하기 위해서, 훈련 중에 일부 hyperparameters를 조정하는 게 괜찮습니다. 이런 특징이 있습니다:
-
For learning rate,
alpha는, 1에 근접한 값으로 시작하고, 파라이터를 계속 줄이게 됩니다. 시간이 지나고, Q-Table에서 좋은 확률 값을 얻으므로, 새로운 값으로 완전히 덮지않고, 살짝 조정하게 됩니다. -
Increase epsilon. 덜 explore하고 더 exploit하려고,
epsilon을 천천히 증가하기 원할 수 있습니다.epsilon의 낮은 값으로 시작하고, 1에 가까이 올리는 것이 괜찮습니다.
Task 1: hyperparameter 값으로 플레이하고 높은 누적 보상에 달성할 수 있는지 확인합니다. 195보다 더 얻을 수 있나요?
Task 2: 정식으로 문제를 해결하려면, 100번 연속으로 195개 평균 보상을 얻을 필요가 있습니다. 훈련하면서 측정하고 공식적으로 문제를 해결했는지 확인합니다!
실행 결과 보기
실제로 훈련된 모델이 어떻게 동작하는지 보는 것은 흥미롭습니다. 시뮬레이션을 돌리고 Q-Table 확률 분포에 따라서 샘플링된, 훈련을 하는 동안 같은 액션 선택 전략으로 따라갑니다: (code block 13)
obs = env.reset()
done = False
while not done:
s = discretize(obs)
env.render()
v = probs(np.array(qvalues(s)))
a = random.choices(actions,weights=v)[0]
obs,_,done,_ = env.step(a)
env.close()
이렇게 보입니다:
🚀 도전
Task 3: 여기, Q-Table의 최종 복사본을 사용하는 게, 최고가 아닐 수 있습니다. 최적-성능을 내는 Q-Table로
Qbest변수를 저장했다는 점을 기억합니다!Qbest를Q에 복사한 최적-성능을 내는 Q-Table로 같은 예시를 시도하고 다른 점을 파악합니다.
Task 4: 여기에는 각 단계에서 최상의 액션을 선택하지 않고, 일치하는 확률 분포로 샘플링했습니다. 가장 높은 Q-Table 값으로, 항상 최상의 액션을 선택하면 더 합리적인가요?
np.argmax함수로 높은 Q-Table 값에 해당되는 액션 숫자를 찾아서 마무리할 수 있습니다. 이 전략을 구현하고 밸런스를 개선했는지 봅니다.
강의 후 퀴즈
과제: Train a Mountain Car
결론
지금부터 agent에 게임에서 원하는 state를 정의하는 보상 함수로 제공하고, 검색 공간을 지능적으로 탐색할 기회를 주며 좋은 결과로 도달하도록 어떻게 훈련하는지 배웠습니다. discrete적이고 연속 환경의 케이스에서 Q-Learning 알고리즘을 성공적으로 적용했지만, discrete적인 액션으로 했습니다.
Atari 게임 스크린에서의 이미지처럼, 액션 상태 또한 연속적이고, 관찰 공간이 조금 더 복잡해지는 시뮬레이션을 공부하는 것도 중요합니다. 이 문제는 좋은 결과에 도달하기 위해서, neural networks처럼, 더 강한 머신러닝 기술을 자주 사용해야 합니다. 이러한 더 구체적인 토픽은 곧 오게 될 더 어려운 AI 코스의 주제입니다.