26 KiB

Raw Blame History Unescape Escape

Прогнозування часових рядів за допомогою ARIMA

У попередньому уроці ви дізналися трохи про прогнозування часових рядів і завантажили набір даних, що показує коливання електричного навантаження за певний період часу.

🎥 Натисніть на зображення вище, щоб переглянути відео: Короткий вступ до моделей ARIMA. Приклад виконаний у R, але концепції є універсальними.

Тест перед лекцією

Вступ

У цьому уроці ви дізнаєтеся про конкретний спосіб створення моделей за допомогою ARIMA: AutoRegressive Integrated Moving Average. Моделі ARIMA особливо добре підходять для аналізу даних, які демонструють нестаціонарність.

Загальні концепції

Щоб працювати з ARIMA, необхідно знати кілька ключових понять:

🎓 Стаціонарність. У статистичному контексті стаціонарність означає дані, розподіл яких не змінюється при зсуві в часі. Нестаціонарні дані, навпаки, демонструють коливання через тренди, які потрібно трансформувати для аналізу. Наприклад, сезонність може викликати коливання в даних, які можна усунути шляхом "сезонного диференціювання".
🎓 Диференціювання. Диференціювання даних у статистичному контексті означає процес трансформації нестаціонарних даних для перетворення їх у стаціонарні шляхом усунення неконстантного тренду. "Диференціювання усуває зміни рівня часових рядів, ліквідуючи тренд і сезонність, тим самим стабілізуючи середнє значення часових рядів." Стаття Шіксіонга та ін.

ARIMA у контексті часових рядів

Розглянемо складові ARIMA, щоб краще зрозуміти, як вона допомагає моделювати часові ряди та робити прогнози.

AR - Автокореляція. Автокореляційні моделі, як випливає з назви, аналізують попередні значення ваших даних, щоб зробити припущення про них. Ці попередні значення називаються "лагами". Наприклад, дані, що показують щомісячні продажі олівців. Загальна кількість продажів кожного місяця буде вважатися "змінною, що еволюціонує" в наборі даних. Ця модель будується як "змінна, що еволюціонує, регресується на своїх власних лагових (тобто попередніх) значеннях." wikipedia
I - Інтеграція. На відміну від схожих моделей 'ARMA', 'I' в ARIMA означає її інтегровану складову. Дані стають "інтегрованими", коли застосовуються кроки диференціювання для усунення нестаціонарності.
MA - Змінне середнє. Складова змінного середнього цієї моделі стосується вихідної змінної, яка визначається шляхом спостереження за поточними та минулими значеннями лагів.

Суть: ARIMA використовується для того, щоб модель максимально точно відповідала особливій формі даних часових рядів.

Вправа - створення моделі ARIMA

Відкрийте папку /working у цьому уроці та знайдіть файл notebook.ipynb.

Запустіть ноутбук, щоб завантажити бібліотеку Python statsmodels; вона знадобиться для моделей ARIMA.
Завантажте необхідні бібліотеки.

Тепер завантажте кілька додаткових бібліотек, корисних для побудови графіків:

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape
from IPython.display import Image

%matplotlib inline
pd.options.display.float_format = '{:,.2f}'.format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore") # specify to ignore warning messages

Завантажте дані з файлу /data/energy.csv у Pandas DataFrame і перегляньте їх:
```
energy = load_data('./data')[['load']]
energy.head(10)
```
Побудуйте графік усіх доступних даних про енергію з січня 2012 року по грудень 2014 року. Ніяких сюрпризів не буде, оскільки ми бачили ці дані в попередньому уроці:
```
energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Тепер давайте створимо модель!

Створення навчальних і тестових наборів даних

Тепер ваші дані завантажені, і ви можете розділити їх на навчальний і тестовий набори. Ви будете тренувати свою модель на навчальному наборі. Як завжди, після завершення навчання моделі ви оціните її точність за допомогою тестового набору. Ви повинні переконатися, що тестовий набір охоплює більш пізній період часу, ніж навчальний, щоб модель не отримала інформацію з майбутніх періодів часу.

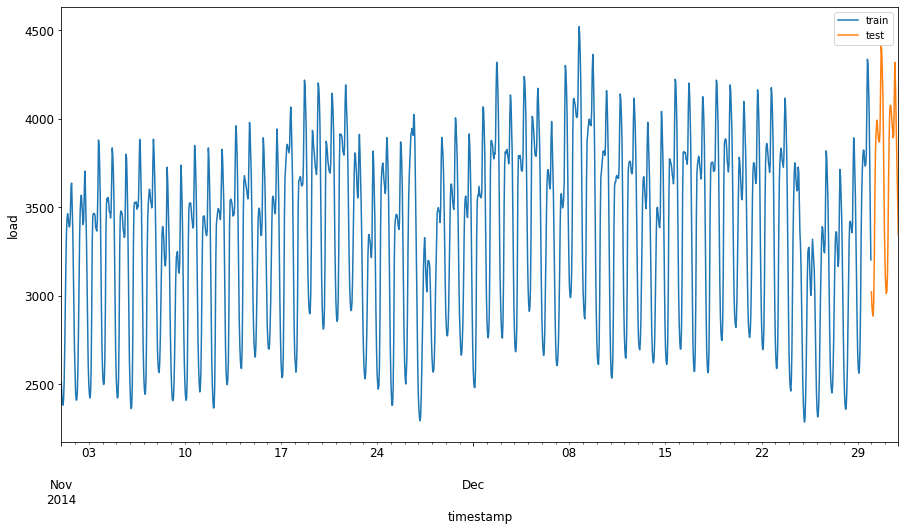
Виділіть двомісячний період з 1 вересня по 31 жовтня 2014 року для навчального набору. Тестовий набір включатиме двомісячний період з 1 листопада по 31 грудня 2014 року:
```
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
```
Оскільки ці дані відображають щоденне споживання енергії, існує сильна сезонна закономірність, але споживання найбільш схоже на споживання в більш недавні дні.
Візуалізуйте відмінності:
```
energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Таким чином, використання відносно невеликого періоду часу для навчання даних має бути достатнім.

Примітка: Оскільки функція, яку ми використовуємо для підгонки моделі ARIMA, використовує внутрішньовибіркову валідацію під час підгонки, ми пропустимо дані для валідації.

Підготовка даних до навчання

Тепер вам потрібно підготувати дані до навчання, виконавши фільтрацію та масштабування даних. Відфільтруйте ваш набір даних, щоб включити лише потрібні періоди часу та стовпці, а також масштабування, щоб дані були представлені в інтервалі 0,1.

Відфільтруйте оригінальний набір даних, щоб включити лише зазначені періоди часу для кожного набору та лише потрібний стовпець 'load' плюс дату:

train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)

Ви можете побачити форму даних:

Training data shape:  (1416, 1)
Test data shape:  (48, 1)

Масштабуйте дані, щоб вони були в діапазоні (0, 1).

scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
train.head(10)

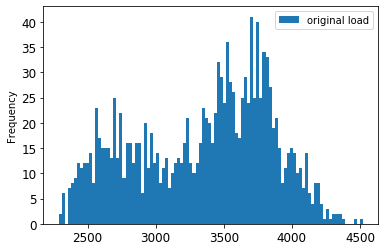
Візуалізуйте оригінальні та масштабовані дані:

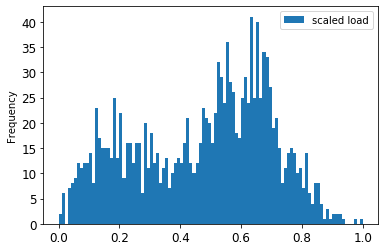
energy[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']].rename(columns={'load':'original load'}).plot.hist(bins=100, fontsize=12)
train.rename(columns={'load':'scaled load'}).plot.hist(bins=100, fontsize=12)
plt.show()

Оригінальні дані

Масштабовані дані

Тепер, коли ви відкалібрували масштабовані дані, ви можете масштабувати тестові дані:
```
test['load'] = scaler.transform(test)
test.head()
```

Реалізація ARIMA

Настав час реалізувати ARIMA! Тепер ви будете використовувати бібліотеку statsmodels, яку ви встановили раніше.

Тепер вам потрібно виконати кілька кроків:

Визначте модель, викликавши SARIMAX() і передавши параметри моделі: параметри p, d і q, а також параметри P, D і Q.
Підготуйте модель для навчальних даних, викликавши функцію fit().
Зробіть прогнози, викликавши функцію forecast() і вказавши кількість кроків (горизонт), які потрібно прогнозувати.

🎓 Що означають всі ці параметри? У моделі ARIMA є 3 параметри, які використовуються для моделювання основних аспектів часових рядів: сезонності, тренду та шуму. Ці параметри:

p: параметр, пов'язаний з автокореляційною складовою моделі, яка враховує попередні значення. d: параметр, пов'язаний з інтегрованою частиною моделі, який впливає на кількість диференціювань (🎓 пам'ятаєте диференціювання 👆?) для застосування до часових рядів. q: параметр, пов'язаний із складовою змінного середнього моделі.

Примітка: Якщо ваші дані мають сезонний аспект - як у цьому випадку - , ми використовуємо сезонну модель ARIMA (SARIMA). У цьому випадку потрібно використовувати інший набір параметрів: P, D і Q, які описують ті ж асоціації, що й p, d і q, але відповідають сезонним компонентам моделі.

Почніть із встановлення бажаного значення горизонту. Спробуємо 3 години:
```
# Specify the number of steps to forecast ahead
HORIZON = 3
print('Forecasting horizon:', HORIZON, 'hours')
```
Вибір найкращих значень для параметрів моделі ARIMA може бути складним, оскільки це дещо суб'єктивно і потребує часу. Ви можете розглянути можливість використання функції auto_arima() з бібліотеки pyramid.

Поки що спробуйте кілька ручних варіантів, щоб знайти хорошу модель.

order = (4, 1, 0)
seasonal_order = (1, 1, 0, 24)

model = SARIMAX(endog=train, order=order, seasonal_order=seasonal_order)
results = model.fit()

print(results.summary())

Виводиться таблиця результатів.

Ви створили свою першу модель! Тепер нам потрібно знайти спосіб її оцінити.

Оцінка вашої моделі

Щоб оцінити вашу модель, ви можете виконати так звану валідацію walk forward. На практиці моделі часових рядів перенавчаються кожного разу, коли стають доступними нові дані. Це дозволяє моделі робити найкращий прогноз на кожному кроці часу.

Починаючи з початку часових рядів, використовуючи цю техніку, навчіть модель на навчальному наборі даних. Потім зробіть прогноз на наступний крок часу. Прогноз оцінюється порівняно з відомим значенням. Навчальний набір потім розширюється, щоб включити відоме значення, і процес повторюється.

Примітка: Ви повинні зберігати фіксоване вікно навчального набору для більш ефективного навчання, щоб кожного разу, коли ви додаєте нове спостереження до навчального набору, ви видаляли спостереження з початку набору.

Цей процес забезпечує більш надійну оцінку того, як модель буде працювати на практиці. Однак це має обчислювальну вартість створення такої кількості моделей. Це прийнятно, якщо дані невеликі або модель проста, але може бути проблемою в масштабі.

Валідація walk forward є золотим стандартом оцінки моделей часових рядів і рекомендується для ваших власних проєктів.

Спочатку створіть тестову точку даних для кожного кроку HORIZON.

test_shifted = test.copy()

for t in range(1, HORIZON+1):
    test_shifted['load+'+str(t)] = test_shifted['load'].shift(-t, freq='H')

test_shifted = test_shifted.dropna(how='any')
test_shifted.head(5)

		load	load+1	load+2
2014-12-30	00:00:00	0.33	0.29	0.27
2014-12-30	01:00:00	0.29	0.27	0.27
2014-12-30	02:00:00	0.27	0.27	0.30
2014-12-30	03:00:00	0.27	0.30	0.41
2014-12-30	04:00:00	0.30	0.41	0.57

Дані зміщуються горизонтально відповідно до їхньої точки горизонту.

Зробіть прогнози для ваших тестових даних, використовуючи цей підхід ковзного вікна в циклі розміром довжини тестових даних:

%%time
training_window = 720 # dedicate 30 days (720 hours) for training

train_ts = train['load']
test_ts = test_shifted

history = [x for x in train_ts]
history = history[(-training_window):]

predictions = list()

order = (2, 1, 0)
seasonal_order = (1, 1, 0, 24)

for t in range(test_ts.shape[0]):
    model = SARIMAX(endog=history, order=order, seasonal_order=seasonal_order)
    model_fit = model.fit()
    yhat = model_fit.forecast(steps = HORIZON)
    predictions.append(yhat)
    obs = list(test_ts.iloc[t])
    # move the training window
    history.append(obs[0])
    history.pop(0)
    print(test_ts.index[t])
    print(t+1, ': predicted =', yhat, 'expected =', obs)

Ви можете спостерігати за процесом навчання:

2014-12-30 00:00:00
1 : predicted = [0.32 0.29 0.28] expected = [0.32945389435989236, 0.2900626678603402, 0.2739480752014323]

2014-12-30 01:00:00
2 : predicted = [0.3  0.29 0.3 ] expected = [0.2900626678603402, 0.2739480752014323, 0.26812891674127126]

2014-12-30 02:00:00
3 : predicted = [0.27 0.28 0.32] expected = [0.2739480752014323, 0.26812891674127126, 0.3025962399283795]

Порівняйте прогнози з фактичним навантаженням:

eval_df = pd.DataFrame(predictions, columns=['t+'+str(t) for t in range(1, HORIZON+1)])
eval_df['timestamp'] = test.index[0:len(test.index)-HORIZON+1]
eval_df = pd.melt(eval_df, id_vars='timestamp', value_name='prediction', var_name='h')
eval_df['actual'] = np.array(np.transpose(test_ts)).ravel()
eval_df[['prediction', 'actual']] = scaler.inverse_transform(eval_df[['prediction', 'actual']])
eval_df.head()

Вивід

		timestamp	h	prediction	actual
0	2014-12-30	00:00:00	t+1	3,008.74	3,023.00
1	2014-12-30	01:00:00	t+1	2,955.53	2,935.00
2	2014-12-30	02:00:00	t+1	2,900.17	2,899.00
3	2014-12-30	03:00:00	t+1	2,917.69	2,886.00
4	2014-12-30	04:00:00	t+1	2,946.99	2,963.00

Спостерігайте за прогнозом даних за годину, порівняно з фактичним навантаженням. Наскільки це точно?

Перевірка точності моделі

Перевірте точність вашої моделі, протестувавши її середню абсолютну процентну помилку (MAPE) для всіх прогнозів.

🧮 Покажіть мені математику

MAPE використовується для демонстрації точності прогнозу як співвідношення, визначеного за формулою вище. Різниця між фактичним і прогнозованим значенням ділиться на фактичне.

"Абсолютне значення в цьому розрахунку підсумовується для кожної прогнозованої точки в часі і ділиться на кількість точок n." wikipedia

Виразіть рівняння у коді:

if(HORIZON > 1):
    eval_df['APE'] = (eval_df['prediction'] - eval_df['actual']).abs() / eval_df['actual']
    print(eval_df.groupby('h')['APE'].mean())

Розрахуйте MAPE для одного кроку:

print('One step forecast MAPE: ', (mape(eval_df[eval_df['h'] == 't+1']['prediction'], eval_df[eval_df['h'] == 't+1']['actual']))*100, '%')

MAPE прогнозу на один крок: 0.5570581332313952 %

Виведіть MAPE для багатокрокового прогнозу:
```
print('Multi-step forecast MAPE: ', mape(eval_df['prediction'], eval_df['actual'])*100, '%')
```
```
Multi-step forecast MAPE:  1.1460048657704118 %
```
Найкраще, коли число низьке: врахуйте, що прогноз із MAPE 10 має похибку в 10%.

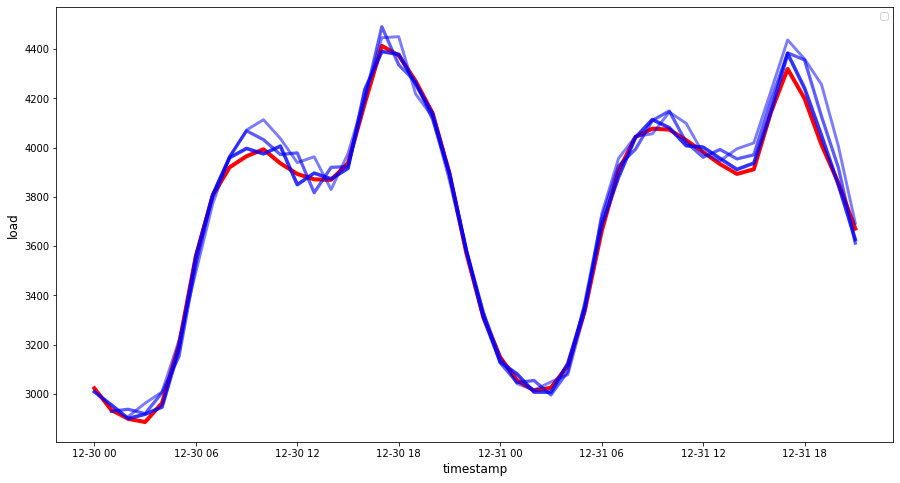
Але, як завжди, легше оцінити точність візуально, тому давайте побудуємо графік:

 if(HORIZON == 1):
    ## Plotting single step forecast
    eval_df.plot(x='timestamp', y=['actual', 'prediction'], style=['r', 'b'], figsize=(15, 8))

else:
    ## Plotting multi step forecast
    plot_df = eval_df[(eval_df.h=='t+1')][['timestamp', 'actual']]
    for t in range(1, HORIZON+1):
        plot_df['t+'+str(t)] = eval_df[(eval_df.h=='t+'+str(t))]['prediction'].values

    fig = plt.figure(figsize=(15, 8))
    ax = plt.plot(plot_df['timestamp'], plot_df['actual'], color='red', linewidth=4.0)
    ax = fig.add_subplot(111)
    for t in range(1, HORIZON+1):
        x = plot_df['timestamp'][(t-1):]
        y = plot_df['t+'+str(t)][0:len(x)]
        ax.plot(x, y, color='blue', linewidth=4*math.pow(.9,t), alpha=math.pow(0.8,t))

    ax.legend(loc='best')

plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

🏆 Дуже гарний графік, який демонструє модель з хорошою точністю. Чудова робота!

🚀Виклик

Досліджуйте способи перевірки точності моделі часових рядів. У цьому уроці ми торкаємося MAPE, але чи є інші методи, які ви могли б використати? Дослідіть їх і додайте коментарі. Корисний документ можна знайти тут

Тест після лекції

Огляд і самостійне навчання

У цьому уроці ми розглядаємо лише основи прогнозування часових рядів за допомогою ARIMA. Приділіть час для поглиблення знань, дослідивши цей репозиторій і його різні типи моделей, щоб дізнатися інші способи створення моделей часових рядів.

Завдання

Нова модель ARIMA

Відмова від відповідальності:
Цей документ було перекладено за допомогою сервісу автоматичного перекладу Co-op Translator. Хоча ми прагнемо до точності, зверніть увагу, що автоматичні переклади можуть містити помилки або неточності. Оригінальний документ мовою оригіналу слід вважати авторитетним джерелом. Для критично важливої інформації рекомендується професійний переклад людиною. Ми не несемо відповідальності за будь-які непорозуміння або неправильні тлумачення, що виникли внаслідок використання цього перекладу.

26 KiB Raw Blame History Unescape Escape