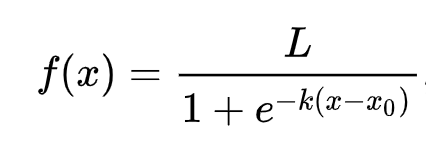17 KiB
Regressão logística para prever categorias
Infográfico por Dasani Madipalli
Questionário inicial
Esta liçao está disponível em R!
Introdução
Nesta lição final sobre Regressão, uma das técnicas básicas do ML clássico, vamos estudar a Regressão Logística. Essa técnica serve para descobrir padrões e prever categorias binárias. Este doce é de chocolate ou não? Esta doença é contagiosa ou não? Este cliente vai escolher este produto ou não?
Você irá aprender:
- Uma nova biblioteca para visualização de dados
- Técnicas de regressão logística
✅ Aprofunde seu conhecimento de como trabalhar com este tipo de regressão neste módulo.
Pré-requisito
Tendo trabalhado com os dados das abóboras, estamos familiarizados o suficiente com eles para perceber que há uma categoria binária com a qual podemos trabalhar: Color (cor).
Vamos construir um modelo de regressão logística para prever qual a cor que a abóbora provavelmente terá (laranja 🎃 ou branca 👻), com base em algumas colunas.
Por que estamos falando de classificação binária em um grupo de lições sobre regressão? Apenas por conveniência linguística, regressão logística é um método de classificação, mesmo sendo linear. Vamos aprender outros modos de classificar dados em lições mais a frente.
Defina a pergunta
Para esta lição, expressaremos 'Orange' (Laranja) ou 'Not Orange' (Não Laranja) como um dado binário. Existe uma categoria 'striped' (listrada) em nosso conjunto de dados, mas há poucas instâncias dela, então não a usaremos. Ela desaparece assim que removemos os valores nulos no conjunto de dados.
🎃 Curiosidade: podemos chamar as abóboras brancas de 'abóboras fantasmas'. Elas não são fáceis de esculpir, por isso não são tão populares quanto as laranjas mas são legais também!
Sobre a regressão logística
A regressão logística difere da regressão linear em alguns aspectos importantes.
Classificação binária
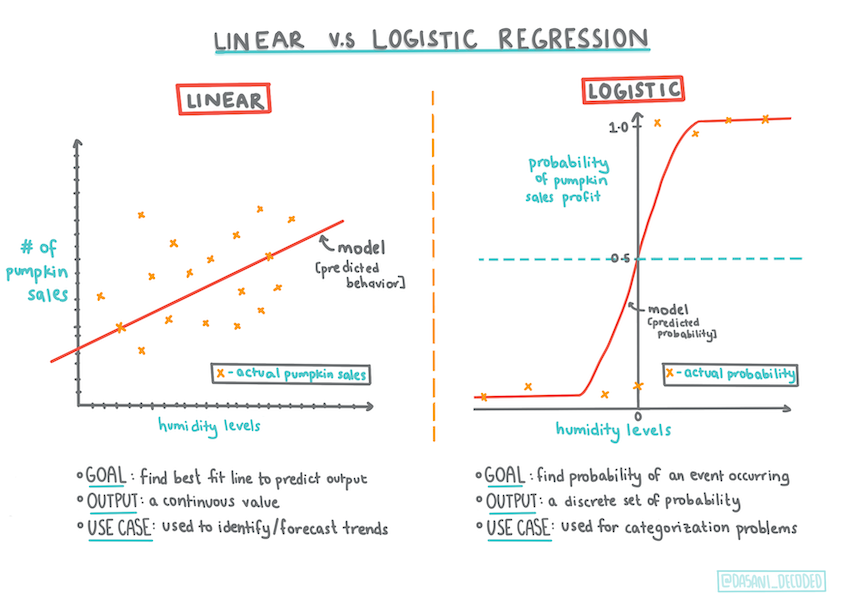
A regressão logística oferece uma previsão sobre uma categoria binária ("laranja ou não laranja"), enquanto a linear é capaz de prever valores contínuos, por exemplo: quanto o preço de uma abóbora vai subir dada sua origem e a época de colheita.
Infográfico por Dasani Madipalli
Outros tipos de classificações
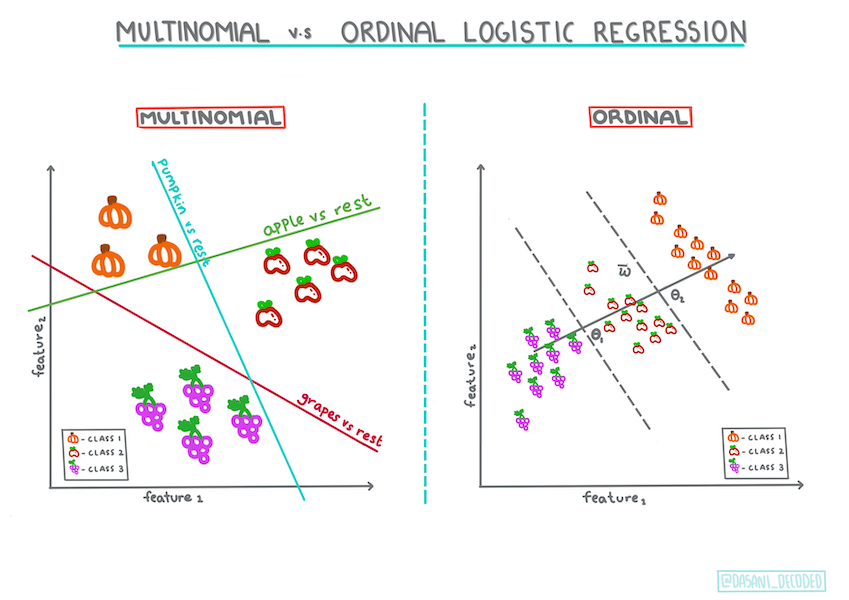
Existem outros tipos de regressão logística, incluindo multinomial e ordinal:
- Multinomial, que envolve ter mais de uma categoria - "Laranja, Branco e Listrado".
- Ordinal, que envolve categorias ordenadas. É útil se quisermos ordenar nossos resultados logicamente, como nossas abóboras que são ordenadas por um número finito de tamanhos (mini, sm, med, lg, xl, xxl).
Infográfico por Dasani Madipalli
Continua sendo linear
Embora esse tipo de regressão esteja relacionado a "previsões de categoria", ele funciona ainda melhor quando há uma relação linear clara entre a variável dependente (cor) e as outras variáveis independentes (o resto do conjunto de dados, como o nome da cidade e as dimensões). É bom saber se existe alguma relação linear entre essas variáveis previamente.
Variáveis NÃO devem ser correlacionadas
Lembra como a regressão linear funcionou melhor com variáveis correlacionadas? A regressão logística é o oposto: as variáveis não precisam disso. Logo, funciona para dados que têm correlações baixas.
Você precisará de muitos dados. E tratados.
A regressão logística fornecerá resultados mais precisos se você usar mais dados; portanto, tenha em mente que, como o conjunto de dados das abóboras é pequeno, talvez não sirva para esta tarefa.
✅ Pense sobre os tipos de dados que funcionariam bem com regressão logística.
Exercício - Organizar os dados
Primeiro, limpamos os dados eliminando os valores nulos e selecionando apenas algumas das colunas:
-
Adicione o seguinte código:
from sklearn.preprocessing import LabelEncoder new_columns = ['Color','Origin','Item Size','Variety','City Name','Package'] new_pumpkins = pumpkins.drop([c for c in pumpkins.columns if c not in new_columns], axis=1) new_pumpkins.dropna(inplace=True) new_pumpkins = new_pumpkins.apply(LabelEncoder().fit_transform)Você pode usar o código abaixo dar uma espiada em como está seu dataframe:
new_pumpkins.info
Visualização: side-by-side grid (grade lado-a-lado)
Após carregar mais uma vez seu notebook com os dados das abóboras e tratá-los para preservar um conjunto de dados contendo algumas colunas, incluindo Color, vamos visualizar o dataframe no notebook usando uma biblioteca diferente: a Seaborn.
Seaborn oferece algumas maneiras interessantes de visualizar dados. Por exemplo, você pode comparar as distribuições dos dados para cada ponto em uma grade lado-a-lado.
-
Crie a grade instanciando um
PairGrid, usando nossos dados de abóborasnew_pumpkins, seguido pela chamada da funçãomap():import seaborn as sns g = sns.PairGrid(new_pumpkins) g.map(sns.scatterplot)Olhando os dados lado a lado, você pode ver como os dados da coluna
Colorse relacionam com as outras colunas.✅ Consegue imaginar o que podemos explorar, dada essa grade de gráficos de dispersão?
Gráfico swarm
Como Color é uma categoria binária (laranja ou não), ela é chamada de 'dado categórico' e precisa de 'uma abordagem mais especializada para visualização'. Existem outras maneiras de visualizar a relação desta coluna com as outras.
As colunas podem ser visualizadas lado a lado com os gráficos Seaborn.
-
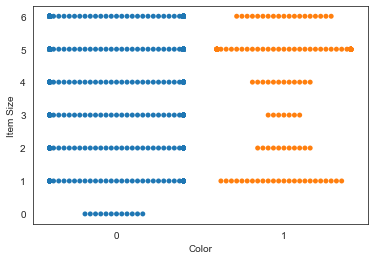
Experimente um gráfico swarm para mostrar a distribuição de valores:
sns.swarmplot(x="Color", y="Item Size", data=new_pumpkins)
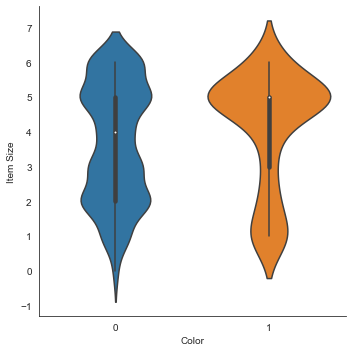
Gráfico violino
Um gráfico do tipo "violino" é útil para visualizar como os dados são distribuídos nas duas categorias. Plotagens semelhantes a violino não funcionam tão bem com conjuntos de dados menores porque a distribuição é exibida de forma mais "uniforme".
-
Use como parâmetros
x=Color,kind="violin"e chame a funçãocatplot():sns.catplot(x="Color", y="Item Size", kind="violin", data=new_pumpkins)✅ Tente criar este gráfico e outros gráficos Seaborn, usando outras colunas.
Agora podemos imaginar a relação entre as duas categorias binárias de cor e tamanho (item size). Vamos explorar a regressão logística para prever a cor de uma abóbora em particular.
🧮 Me mostre a matemática
Você se lembra como a regressão linear costumava usar mínimos quadrados comuns para chegar a um valor? A regressão logística depende do conceito de 'probabilidade máxima' usando funções sigmóide. Uma 'função sigmóide' em um gráfico parece estar na forma de um 'S'. Ela pega um valor e o mapeia para algo entre 0 e 1. Sua curva também é chamada de 'curva logística'. Sua fórmula é assim:
o ponto médio do sigmóide encontra-se no eixo X.
Lé o valor máximo da curva eké a inclinação da curva. Se o resultado da função for maior que 0.5, o valor atribuído à função será classificado como '1'. Caso contrário, será classificado como '0'.
Construindo um modelo
Construir um modelo para encontrar classificações binárias é muito simples no Scikit-learn.
-
Selecione as colunas que deseja usar em seu modelo de classificação e divida os conjuntos de dados em conjuntos de treinamento e teste chamando
train_test_split():from sklearn.model_selection import train_test_split Selected_features = ['Origin','Item Size','Variety','City Name','Package'] X = new_pumpkins[Selected_features] y = new_pumpkins['Color'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) -
Usando seus dados de treinamento, treine seu modelo chamando a função
fit(), e imprima o resultado:from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, classification_report from sklearn.linear_model import LogisticRegression model = LogisticRegression() model.fit(X_train, y_train) predictions = model.predict(X_test) print(classification_report(y_test, predictions)) print('Predicted labels: ', predictions) print('Accuracy: ', accuracy_score(y_test, predictions))Veja o placar do seu modelo. Nada mal, especialmente com apenas 1000 linhas de dados:
precision recall f1-score support 0 0.85 0.95 0.90 166 1 0.38 0.15 0.22 33 accuracy 0.82 199 macro avg 0.62 0.55 0.56 199 weighted avg 0.77 0.82 0.78 199 Predicted labels: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0]
Melhor compreensão usando Matriz de Confusão
Embora você possa obter os valores de um relatório de placar do seu modelo como na impressão acima, você pode entender melhor o desempenho do seu modelo com uma matriz de confusão.
🎓 Uma 'matriz de confusão' (ou 'matriz de erro') é uma tabela que expressa os verdadeiros e falsos positivos e negativos, medindo a acurácia das previsões.
-
Para obter a matriz de confusão, chame a função
confusion_matrix():from sklearn.metrics import confusion_matrix confusion_matrix(y_test, predictions)Dê uma olhada na matriz de confusão do seu modelo:
array([[162, 4], [ 33, 0]])
Na Scikit-learn, as linhas nas matrizes de confusão (eixo 0) são classes reais e colunas (eixo 1) são classes previstas.
0 1 0 TP (True Positive = Verdadeiro Positivo) FN (False Negative = Falso Negativo) 1 FP (False Positive = Falso Positivo) TN (True Negative = Verdadeiro Negativo)
O que está acontecendo aqui? Supondo que nosso modelo tenha que classificar as abóboras entre duas categorias binárias, categoria 'laranja' e categoria 'não laranja':
- Se o seu modelo prevê que uma abóbora não é laranja e ela pertence à categoria 'não laranja', chamamos isso de verdadeiro negativo.
- Se o seu modelo prevê que uma abóbora é laranja e ela pertence à categoria 'não laranja', chamamos isso de falso positivo.
- Se o seu modelo prevê que uma abóbora não é laranja e ela pertence à categoria 'laranja', chamamos isso de falso negativo.
- Se o seu modelo prevê que uma abóbora é laranja e ela pertence à categoria 'laranja', chamamos isso de verdadeiro positivo.
Podemos perceber que é melhor ter um número maior de positivos e negativos verdadeiros e um número menor de positivos e negativos falsos pois, isso significa que o modelo tem um desempenho melhor.
✅ Pergunta: Com base na matriz de confusão, o modelo é bom ou não? Resposta: nada mal; existem muitos verdadeiros positivos (162) e poucos falsos negativos (4).
Vamos revisitar os termos que vimos anteriormente com a ajuda da matriz de confusão de TP / TN e FP / FN:
🎓 Precision: TP / (TP + FP). Razão de dados relevantes que foram previstos corretamente entre todos os dados do conjunto.
🎓 Recall: TP / (TP + FN). A proporção dos dados relevantes que foram previstos, estando rotulados corretamente ou não.
🎓 f1-score (pontuação f1): (2 * precision * recall)/(precision + recall). Uma média ponderada entre precision e recall. 1 é bom e 0 é ruim.
🎓 Support (suporte): O número de ocorrências de cada classe.
🎓 Accuracy (acurácia): (TP + TN) / (TP + TN + FP + FN). Porcentagem de classes previstas corretamente para uma amostra.
🎓 Macro avg (média macro): Média simples (não ponderada) das métricas de cada classe.
🎓 Weighted Avg (média Ponderada): Média ponderada dos valores de Support de cada classe.
Como a matriz de confusão se relaciona com precision (precisão) e recall (cobertura)? A matriz de confusão mostrada acima possui valores de precisão (0.83) e recall (0.98), pois:
Precision = TP / (TP + FP) = 162 / (162 + 33) = 0.8307692307692308
Recall = TP / (TP + FN) = 162 / (162 + 4) = 0.9759036144578314
✅ Você consegue perceber qual métrica deve ser usada se quiser que seu modelo reduza o número de falsos negativos?
Visualizando a curva ROC de um modelo
O modelo construído não é ruim. A acurácia é de cerca de 80%, então ele pode ser usado para prever a cor de uma abóbora com base em algumas colunas.
Vamos usar mais um tipo de visualização utilizando a ROC:
from sklearn.metrics import roc_curve, roc_auc_score
y_scores = model.predict_proba(X_test)
# calculate ROC curve
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])
sns.lineplot([0, 1], [0, 1])
sns.lineplot(fpr, tpr)
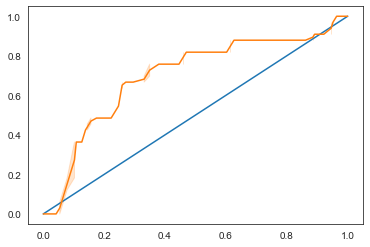
Usando a Seaborn novamente, plote a Receiving Operating Characteristic (Característica de Operação do Receptor) do modelo ou ROC. As curvas ROC são muito usadas para obter uma visão da saída de um classificador em termos de seus verdadeiros versus falsos positivos. "As curvas ROC normalmente apresentam taxa de verdadeiro positivo no eixo Y e taxa de falso positivo no eixo X." Assim, a inclinação da curva e o espaço entre a linha do ponto médio e a curva são importantes: precisamos de uma curva que sobe e passa pela linha. No nosso caso, existem falsos positivos no começo e, em seguida, a linha avança corretamente:
Por fim, usamos a API roc_auc_score da Scikit-learn para calcular a 'Area Under the Curve' (área sob a curva) ou AUC:
auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)
O resultado é 0.6976998904709748. Sabendo que a AUC varia de 0 a 1, o ideal é uma pontuação alta, pois um modelo que está 100% correto em suas previsões terá uma AUC de 1; neste caso, o modelo é muito bom.
Em outras lições sobre classificação, você aprenderá como iterar para melhorar as pontuações do seu modelo. Mas por enquanto, parabéns! Você concluiu as lições sobre regressão!
🚀Desafio
Ainda há muito sobre regressão logística! E a melhor maneira de aprender é experimentando. Encontre um conjunto de dados para este tipo de análise e construa um modelo com ele. O que você aprendeu? dica: tente o Kaggle para conjuntos de dados interessantes.
Questionário para fixação
Revisão e Auto Aprendizagem
Leia as primeiras páginas deste artigo de Stanford sobre alguns usos práticos da regressão logística. Pense nas tarefas mais adequadas para um ou outro tipo de tarefa de regressão que estudamos até agora. O que funcionaria melhor?