11 KiB

Raw Blame History Unescape Escape

Clustering K-Means

🎥 Fare clic sull'immagine sopra per un video: Andrew Ng spiega il clustering

Quiz Pre-Lezione

In questa lezione si imparerà come creare cluster utilizzando Scikit-learn e l'insieme di dati di musica nigeriana importato in precedenza. Si tratteranno le basi di K-Means per Clustering. Si tenga presente che, come appreso nella lezione precedente, ci sono molti modi per lavorare con i cluster e il metodo usato dipende dai propri dati. Si proverà K-Means poiché è la tecnica di clustering più comune. Si inizia!

Temini che si imparerà a conoscere:

Silhouette scoring (punteggio silhouette)
Elbow method (metodo del gomito)
Inerzia
Varianza

Introduzione

K-Means Clustering è un metodo derivato dal campo dell'elaborazione del segnale. Viene utilizzato per dividere e partizionare gruppi di dati in cluster "k" utilizzando una serie di osservazioni. Ogni osservazione lavora per raggruppare un dato punto dati più vicino alla sua "media" più vicina, o punto centrale di un cluster.

I cluster possono essere visualizzati come diagrammi di Voronoi, che includono un punto (o 'seme') e la sua regione corrispondente.

Infografica di Jen Looper

Il processo di clustering K-Means viene eseguito in tre fasi:

L'algoritmo seleziona il numero k di punti centrali campionando dall'insieme di dati. Dopo questo, esegue un ciclo:
1. Assegna ogni campione al centroide più vicino.
2. Crea nuovi centroidi prendendo il valore medio di tutti i campioni assegnati ai centroidi precedenti.
3. Quindi, calcola la differenza tra il nuovo e il vecchio centroide e ripete finché i centroidi non sono stabilizzati.

Uno svantaggio dell'utilizzo di K-Means include il fatto che sarà necessario stabilire 'k', ovvero il numero di centroidi. Fortunatamente il "metodo del gomito" aiuta a stimare un buon valore iniziale per "k". Si proverà in un minuto.

Prerequisito

Si lavorerà nel file notebook.ipynb di questa lezione che include l'importazione dei dati e la pulizia preliminare fatta nell'ultima lezione.

Esercizio - preparazione

Iniziare dando un'altra occhiata ai dati delle canzoni.

Creare un diagramma a scatola e baffi (boxplot), chiamando boxplot() per ogni colonna:

plt.figure(figsize=(20,20), dpi=200)

plt.subplot(4,3,1)
sns.boxplot(x = 'popularity', data = df)

plt.subplot(4,3,2)
sns.boxplot(x = 'acousticness', data = df)

plt.subplot(4,3,3)
sns.boxplot(x = 'energy', data = df)

plt.subplot(4,3,4)
sns.boxplot(x = 'instrumentalness', data = df)

plt.subplot(4,3,5)
sns.boxplot(x = 'liveness', data = df)

plt.subplot(4,3,6)
sns.boxplot(x = 'loudness', data = df)

plt.subplot(4,3,7)
sns.boxplot(x = 'speechiness', data = df)

plt.subplot(4,3,8)
sns.boxplot(x = 'tempo', data = df)

plt.subplot(4,3,9)
sns.boxplot(x = 'time_signature', data = df)

plt.subplot(4,3,10)
sns.boxplot(x = 'danceability', data = df)

plt.subplot(4,3,11)
sns.boxplot(x = 'length', data = df)

plt.subplot(4,3,12)
sns.boxplot(x = 'release_date', data = df)

Questi dati sono un po' rumorosi: osservando ogni colonna come un boxplot, si possono vedere i valori anomali.

Si potrebbe esaminare l'insieme di dati e rimuovere questi valori anomali, ma ciò renderebbe i dati piuttosto minimi.

Per ora, si scelgono quali colonne utilizzare per questo esercizio di clustering. Scegliere quelle con intervalli simili e codifica la colonna artist_top_genre come dati numerici:

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()

X = df.loc[:, ('artist_top_genre','popularity','danceability','acousticness','loudness','energy')]

y = df['artist_top_genre']

X['artist_top_genre'] = le.fit_transform(X['artist_top_genre'])

y = le.transform(y)

Ora si deve scegliere quanti cluster scegliere come obiettivo. E' noto che ci sono 3 generi di canzoni ricavati dall'insieme di dati, quindi si prova 3:

from sklearn.cluster import KMeans

nclusters = 3
seed = 0

km = KMeans(n_clusters=nclusters, random_state=seed)
km.fit(X)

# Predict the cluster for each data point

y_cluster_kmeans = km.predict(X)
y_cluster_kmeans

Viene visualizzato un array con i cluster previsti (0, 1 o 2) per ogni riga del dataframe di dati.

Usare questo array per calcolare un "punteggio silhouette":

from sklearn import metrics
score = metrics.silhouette_score(X, y_cluster_kmeans)
score

Punteggio Silhouette

Si vuole ottenere un punteggio silhouette più vicino a 1. Questo punteggio varia da -1 a 1 e, se il punteggio è 1, il cluster è denso e ben separato dagli altri cluster. Un valore vicino a 0 rappresenta cluster sovrapposti con campioni molto vicini al limite di decisione dei clusters vicini fonte.

Il punteggio è .53, quindi proprio nel mezzo. Ciò indica che i dati non sono particolarmente adatti a questo tipo di clustering, ma si prosegue.

Esercizio: costruire il proprio modello

Importare KMeans e avviare il processo di clustering.
```
from sklearn.cluster import KMeans
wcss = []

for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)
```
Ci sono alcune parti qui che meritano una spiegazione.

🎓 range: queste sono le iterazioni del processo di clustering

🎓 random_state: "Determina la generazione di numeri casuali per l'inizializzazione del centroide."fonte

🎓 WCSS: "somma dei quadrati all'interno del cluster" misura la distanza media al quadrato di tutti i punti all'interno di un cluster rispetto al cluster centroid fonte.

🎓 Inerzia: gli algoritmi K-Means tentano di scegliere i centroidi per ridurre al minimo l’’inerzia’, "una misura di quanto siano coerenti i cluster".fonte. Il valore viene aggiunto alla variabile wcss ad ogni iterazione.

🎓 k-means++: in Scikit-learn puoi utilizzare l'ottimizzazione 'k-means++', che "inizializza i centroidi in modo che siano (generalmente) distanti l'uno dall'altro, portando probabilmente a risultati migliori rispetto all'inizializzazione casuale.

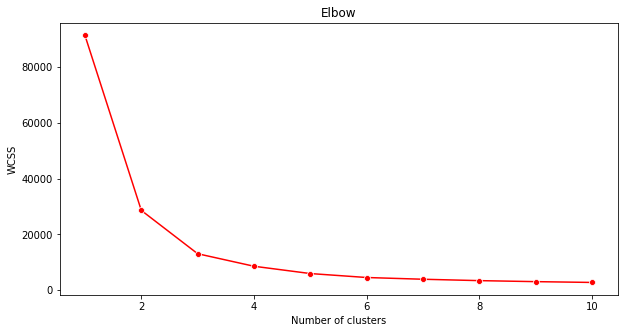
Metodo del gomito

In precedenza, si era supposto che, poiché sono stati presi di mira 3 generi di canzoni, si dovrebbero scegliere 3 cluster. E' questo il caso?

Usare il "metodo del gomito" per assicurarsene.
```
plt.figure(figsize=(10,5))
sns.lineplot(range(1, 11), wcss,marker='o',color='red')
plt.title('Elbow')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
```
Usare la variabile wcss creata nel passaggio precedente per creare un grafico che mostra dove si trova la "piegatura" nel gomito, che indica il numero ottimale di cluster. Forse sono 3!

Esercizio - visualizzare i cluster

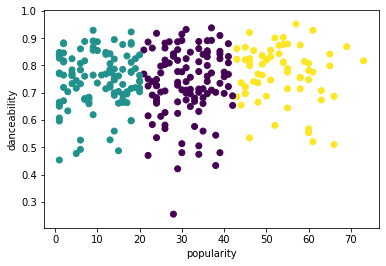
Riprovare il processo, questa volta impostando tre cluster e visualizzare i cluster come grafico a dispersione:

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
labels = kmeans.predict(X)
plt.scatter(df['popularity'],df['danceability'],c = labels)
plt.xlabel('popularity')
plt.ylabel('danceability')
plt.show()

Verificare la precisione del modello:
```
labels = kmeans.labels_

correct_labels = sum(y == labels)

print("Result: %d out of %d samples were correctly labeled." % (correct_labels, y.size))

print('Accuracy score: {0:0.2f}'. format(correct_labels/float(y.size)))
```
La precisione di questo modello non è molto buona e la forma dei grappoli fornisce un indizio sul perché.

Questi dati sono troppo sbilanciati, troppo poco correlati e c'è troppa varianza tra i valori della colonna per raggruppare bene. In effetti, i cluster che si formano sono probabilmente fortemente influenzati o distorti dalle tre categorie di genere definite sopra. È stato un processo di apprendimento!

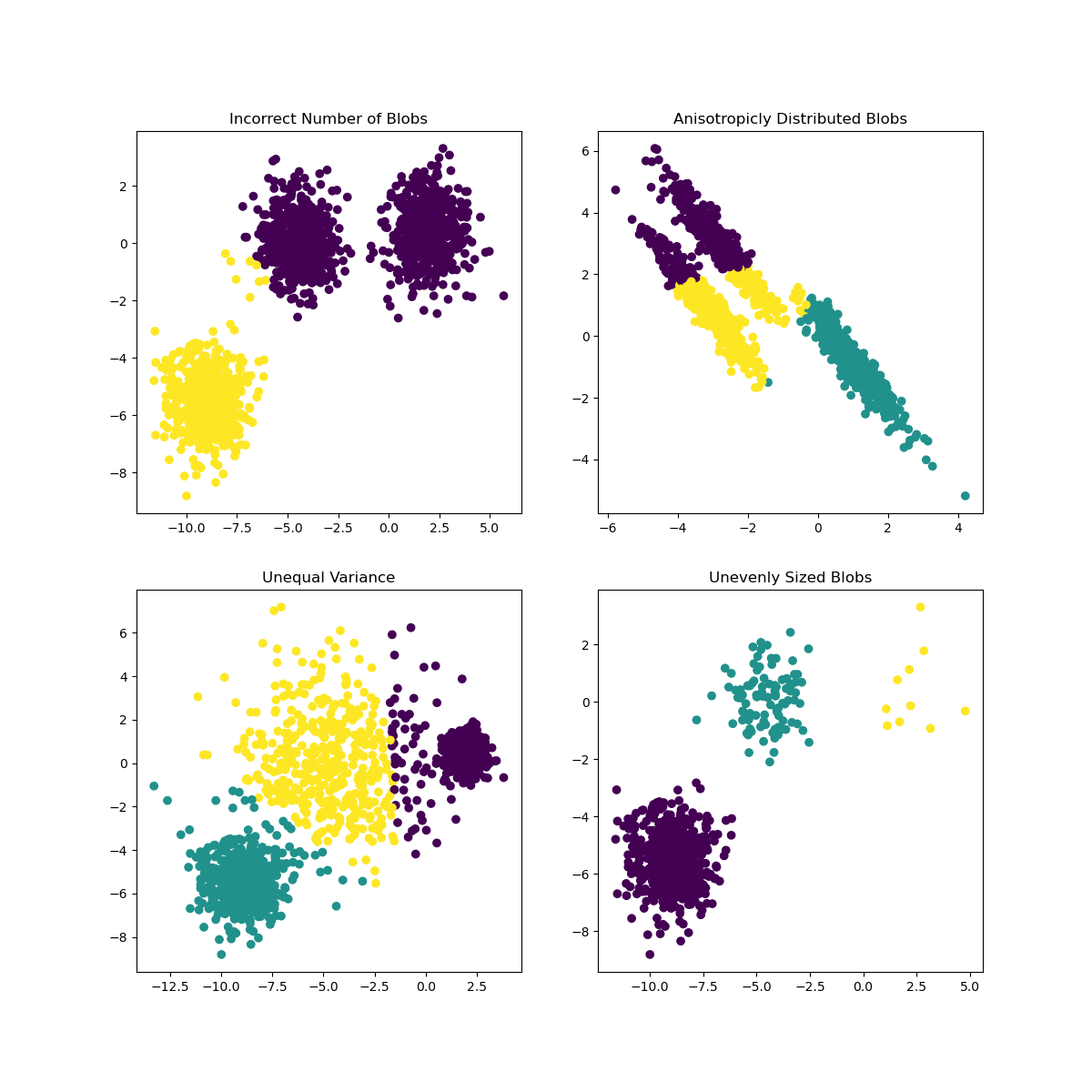
Nella documentazione di Scikit-learn, si può vedere che un modello come questo, con cluster non molto ben delimitati, ha un problema di "varianza":

Infografica da Scikit-learn

Varianza

La varianza è definita come "la media delle differenze al quadrato dalla media" fonte. Nel contesto di questo problema di clustering, si fa riferimento ai dati che i numeri dell'insieme di dati tendono a divergere un po' troppo dalla media.

✅ Questo è un ottimo momento per pensare a tutti i modi in cui si potrebbe correggere questo problema. Modificare un po' di più i dati? Utilizzare colonne diverse? Utilizzare un algoritmo diverso? Suggerimento: provare a ridimensionare i dati per normalizzarli e testare altre colonne.

Provare questo "calcolatore della varianza" per capire un po’ di più il concetto.

🚀 Sfida

Trascorrere un po' di tempo con questo notebook, modificando i parametri. E possibile migliorare l'accuratezza del modello pulendo maggiormente i dati (rimuovendo gli outlier, ad esempio)? È possibile utilizzare i pesi per dare più peso a determinati campioni di dati. Cos'altro si può fare per creare cluster migliori?

Suggerimento: provare a ridimensionare i dati. C'è un codice commentato nel notebook che aggiunge il ridimensionamento standard per rendere le colonne di dati più simili tra loro in termini di intervallo. Si scoprirà che mentre il punteggio della silhouette diminuisce, il "kink" nel grafico del gomito si attenua. Questo perché lasciare i dati non scalati consente ai dati con meno varianza di avere più peso. Leggere un po' di più su questo problema qui.

Quiz post-lezione

Revisione e Auto Apprendimento

Dare un'occhiata a un simulatore di K-Means tipo questo. È possibile utilizzare questo strumento per visualizzare i punti dati di esempio e determinarne i centroidi. Questo aiuta a farsi un'idea di come i dati possono essere raggruppati?

Inoltre, dare un'occhiata a questa dispensa sui k-means di Stanford.

Compito

Provare diversi metodi di clustering

11 KiB Raw Blame History Unescape Escape