15 KiB

Raw Blame History Unescape Escape

Costruire un modello di regressione usando Scikit-learn: regressione in due modi

Infografica di Dasani Madipalli

Quiz pre-lezione

Introduzione

Finora si è esplorato cos'è la regressione con dati di esempio raccolti dall'insieme di dati relativo ai prezzi della zucca, che verrà usato in questa lezione. Lo si è anche visualizzato usando Matplotlib.

Ora si è pronti per approfondire la regressione per machine learning. In questa lezione si imparerà di più su due tipi di regressione: regressione lineare di base e regressione polinomiale, insieme ad alcuni dei calcoli alla base di queste tecniche.

In questo programma di studi, si assume una conoscenza minima della matematica, e si cerca di renderla accessibile agli studenti provenienti da altri campi, quindi si faccia attenzione a note, 🧮 didascalie, diagrammi e altri strumenti di apprendimento che aiutano la comprensione.

Prerequisito

Si dovrebbe ormai avere familiarità con la struttura dei dati della zucca che si sta esaminando. Lo si può trovare precaricato e prepulito nel file notebook.ipynb di questa lezione. Nel file, il prezzo della zucca viene visualizzato per bushel (staio) in un nuovo dataframe. Assicurasi di poter eseguire questi notebook nei kernel in Visual Studio Code.

Preparazione

Come promemoria, si stanno caricando questi dati in modo da porre domande su di essi.

Qual è il momento migliore per comprare le zucche?
Che prezzo ci si può aspettare da una cassa di zucche in miniatura?
Si devono acquistare in cestini da mezzo bushel o a scatola da 1 1/9 bushel? Si continua a scavare in questi dati.

Nella lezione precedente, è stato creato un dataframe Pandas e si è popolato con parte dell'insieme di dati originale, standardizzando il prezzo per lo bushel. In questo modo, tuttavia, si sono potuti raccogliere solo circa 400 punti dati e solo per i mesi autunnali.

Si dia un'occhiata ai dati precaricati nel notebook di accompagnamento di questa lezione. I dati sono precaricati e viene tracciato un grafico a dispersione iniziale per mostrare i dati mensili. Forse si può ottenere qualche dettaglio in più sulla natura dei dati pulendoli ulteriormente.

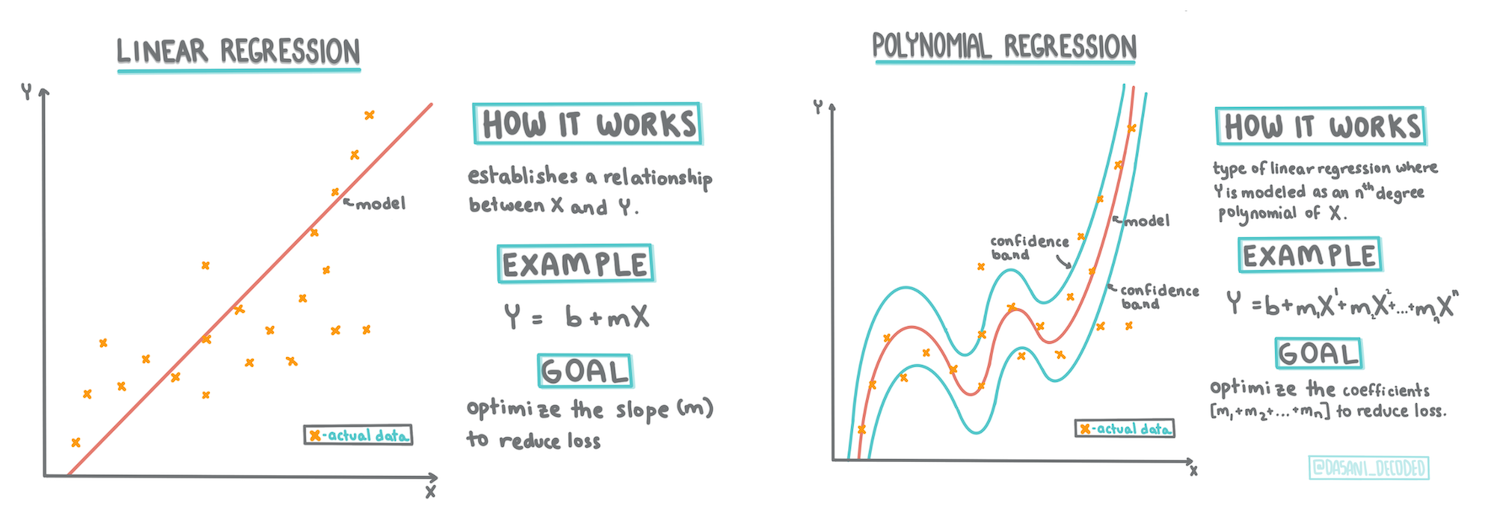
Una linea di regressione lineare

Come si è appreso nella lezione 1, l'obiettivo di un esercizio di regressione lineare è essere in grado di tracciare una linea per:

Mostrare le relazioni tra variabili.
Fare previsioni. Fare previsioni accurate su dove cadrebbe un nuovo punto dati in relazione a quella linea.

È tipico della Regressione dei Minimi Quadrati disegnare questo tipo di linea. Il termine "minimi quadrati" significa che tutti i punti dati che circondano la linea di regressione sono elevati al quadrato e quindi sommati. Idealmente, quella somma finale è la più piccola possibile, perché si vuole un basso numero di errori, o minimi quadrati.

Lo si fa perché si vuole modellare una linea che abbia la distanza cumulativa minima da tutti i punti dati. Si esegue anche il quadrato dei termini prima di aggiungerli poiché interessa la grandezza piuttosto che la direzione.

🧮 Mostrami la matematica

Questa linea, chiamata linea di miglior adattamento , può essere espressa da un'equazione:
Y = a + bX
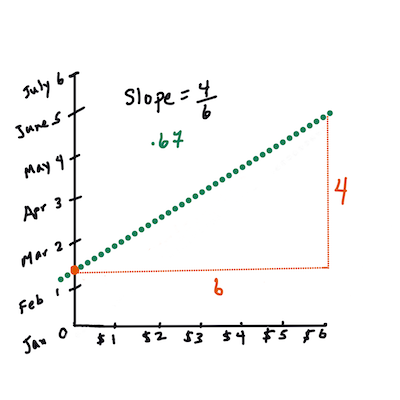
X è la "variabile esplicativa". Y è la "variabile dipendente". La pendenza della linea è b e a è l'intercetta di y, che si riferisce al valore di Y quando X = 0.

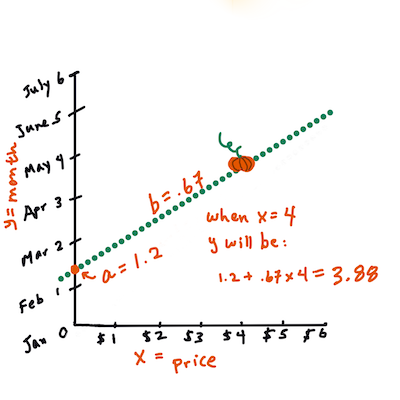
Prima, calcolare la pendenza b. Infografica di Jen Looper

In altre parole, facendo riferimento alla domanda originale per i dati sulle zucche: "prevedere il prezzo di una zucca per bushel per mese", X si riferisce al prezzo e Y si riferirisce al mese di vendita.

Si calcola il valore di Y. Se si sta pagando circa $4, deve essere aprile! Infografica di Jen Looper

La matematica che calcola la linea deve dimostrare la pendenza della linea, che dipende anche dall'intercetta, o dove Y si trova quando X = 0.

Si può osservare il metodo di calcolo per questi valori sul sito web Math is Fun . Si visiti anche questo calcolatore dei minimi quadrati per vedere come i valori dei numeri influiscono sulla linea.

Correlazione

Un altro termine da comprendere è il Coefficiente di Correlazione tra determinate variabili X e Y. Utilizzando un grafico a dispersione, è possibile visualizzare rapidamente questo coefficiente. Un grafico con punti dati sparsi in una linea ordinata ha un'alta correlazione, ma un grafico con punti dati sparsi ovunque tra X e Y ha una bassa correlazione.

Un buon modello di regressione lineare sarà quello che ha un Coefficiente di Correlazione alto (più vicino a 1 rispetto a 0) utilizzando il Metodo di Regressione dei Minimi Quadrati con una linea di regressione.

✅ Eseguire il notebook che accompagna questa lezione e guardare il grafico a dispersione City to Price. I dati che associano la città al prezzo per le vendite di zucca sembrano avere una correlazione alta o bassa, secondo la propria interpretazione visiva del grafico a dispersione?

Preparare i dati per la regressione

Ora che si ha una comprensione della matematica alla base di questo esercizio, si crea un modello di regressione per vedere se si può prevedere quale pacchetto di zucche avrà i migliori prezzi per zucca. Qualcuno che acquista zucche per una festa con tema un campo di zucche potrebbe desiderare che queste informazioni siano in grado di ottimizzare i propri acquisti di pacchetti di zucca per il campo.

Dal momento che si utilizzerà Scikit-learn, non c'è motivo di farlo a mano (anche se si potrebbe!). Nel blocco di elaborazione dati principale del notebook della lezione, aggiungere una libreria da Scikit-learn per convertire automaticamente tutti i dati di tipo stringa in numeri:

from sklearn.preprocessing import LabelEncoder

new_pumpkins.iloc[:, 0:-1] = new_pumpkins.iloc[:, 0:-1].apply(LabelEncoder().fit_transform)

Se si guarda ora il dataframe new_pumpkins, si vede che tutte le stringhe ora sono numeriche. Questo rende più difficile la lettura per un umano ma molto più comprensibile per Scikit-learn! Ora si possono prendere decisioni più consapevoli (non solo basate sull'osservazione di un grafico a dispersione) sui dati più adatti alla regressione.

Si provi a trovare una buona correlazione tra due punti nei propri dati per costruire potenzialmente un buon modello predittivo. A quanto pare, c'è solo una debole correlazione tra la città e il prezzo:

print(new_pumpkins['City'].corr(new_pumpkins['Price']))
0.32363971816089226

Tuttavia, c'è una correlazione leggermente migliore tra il pacchetto e il suo prezzo. Ha senso, vero? Normalmente, più grande è la scatola dei prodotti, maggiore è il prezzo.

print(new_pumpkins['Package'].corr(new_pumpkins['Price']))
0.6061712937226021

Una buona domanda da porre a questi dati sarà: "Che prezzo posso aspettarmi da un determinato pacchetto di zucca?"

Si costruisce questo modello di regressione

Costruire un modello lineare

Prima di costruire il modello, si esegue un altro riordino dei dati. Si eliminano tutti i dati nulli e si controlla ancora una volta che aspetto hanno i dati.

new_pumpkins.dropna(inplace=True)
new_pumpkins.info()

Quindi, si crea un nuovo dataframe da questo set minimo e lo si stampa:

new_columns = ['Package', 'Price']
lin_pumpkins = new_pumpkins.drop([c for c in new_pumpkins.columns if c not in new_columns], axis='columns')

lin_pumpkins

	Package	Price
70	0	13.636364
71	0	16.363636
72	0	16.363636
73	0	15.454545
74	0	13.636364
...	...	...
1738	2	30.000000
1739	2	28.750000
1740	2	25.750000
1741	2	24.000000
1742	2	24.000000
415 rows × 2 columns

Ora si possono assegnare i dati delle coordinate X e y:

X = lin_pumpkins.values[:, :1]
y = lin_pumpkins.values[:, 1:2]

Cosa sta succedendo qui? Si sta usando la notazione slice Python per creare array per popolare X e y.

Successivamente, si avvia le routine di creazione del modello di regressione:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)

pred = lin_reg.predict(X_test)

accuracy_score = lin_reg.score(X_train,y_train)
print('Model Accuracy: ', accuracy_score)

Poiché la correlazione non è particolarmente buona, il modello prodotto non è molto accurato.

Model Accuracy:  0.3315342327998987

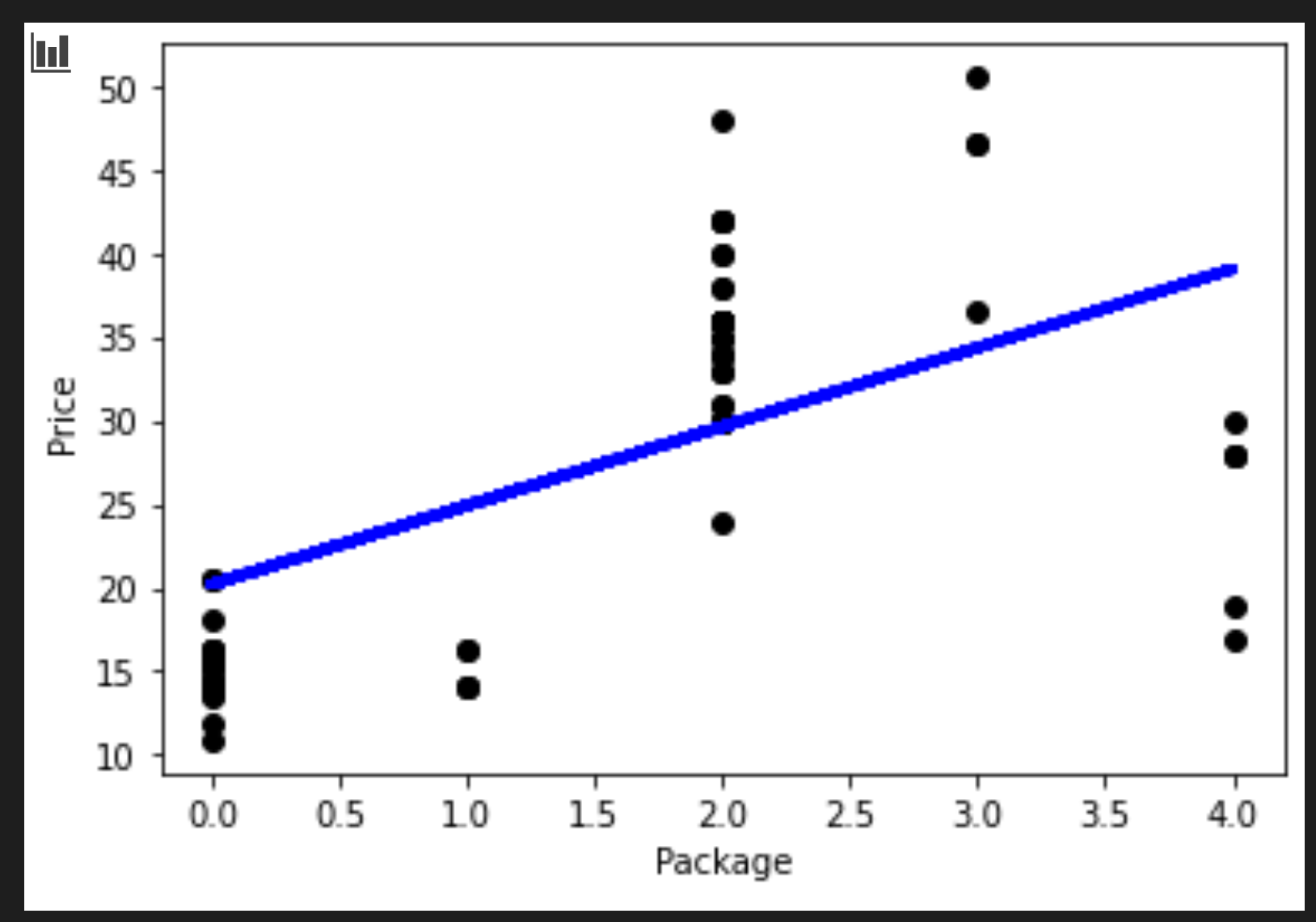
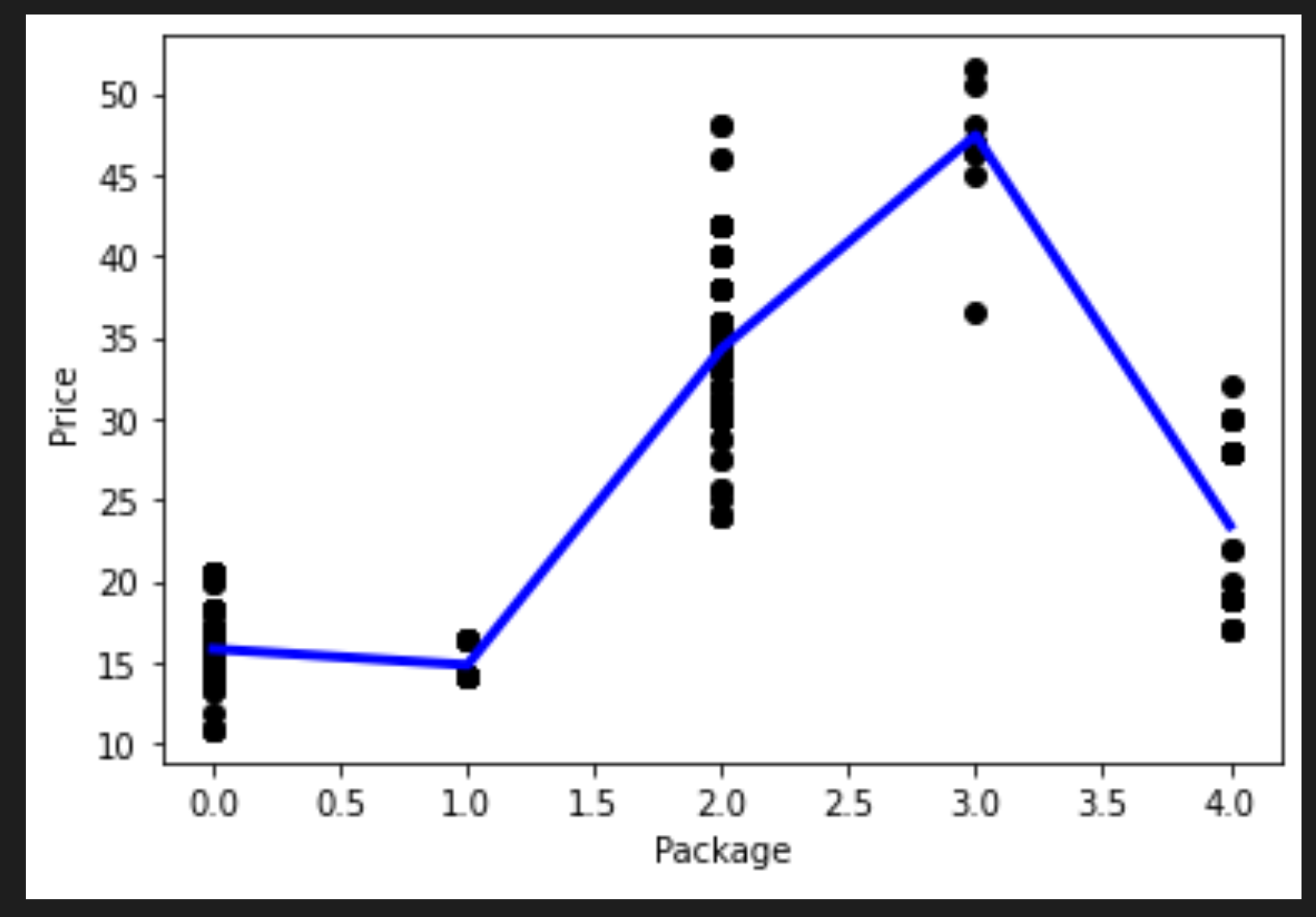
Si può visualizzare la linea tracciata nel processo:

plt.scatter(X_test, y_test,  color='black')
plt.plot(X_test, pred, color='blue', linewidth=3)

plt.xlabel('Package')
plt.ylabel('Price')

plt.show()

Si testa il modello contro una varietà ipotetica:
```
lin_reg.predict( np.array([ [2.75] ]) )
```
Il prezzo restituito per questa varietà mitologica è:
```
array([[33.15655975]])
```

Quel numero ha senso, se la logica della linea di regressione è vera.

🎃 Congratulazioni, si è appena creato un modello che può aiutare a prevedere il prezzo di alcune varietà di zucche. La zucca per le festività sarà bellissima. Ma probabilmente si può creare un modello migliore!

Regressione polinomiale

Un altro tipo di regressione lineare è la regressione polinomiale. Mentre a volte c'è una relazione lineare tra le variabili - più grande è il volume della zucca, più alto è il prezzo - a volte queste relazioni non possono essere tracciate come un piano o una linea retta.

✅ Ecco alcuni altri esempi di dati che potrebbero utilizzare la regressione polinomiale

Si dia un'altra occhiata alla relazione tra Varietà e Prezzo nel tracciato precedente. Questo grafico a dispersione deve essere necessariamente analizzato da una linea retta? Forse no. In questo caso, si può provare la regressione polinomiale.

✅ I polinomi sono espressioni matematiche che possono essere costituite da una o più variabili e coefficienti

La regressione polinomiale crea una linea curva per adattare meglio i dati non lineari.

Viene ricreato un dataframe popolato con un segmento dei dati della zucca originale:

new_columns = ['Variety', 'Package', 'City', 'Month', 'Price']
poly_pumpkins = new_pumpkins.drop([c for c in new_pumpkins.columns if c not in new_columns], axis='columns')

poly_pumpkins

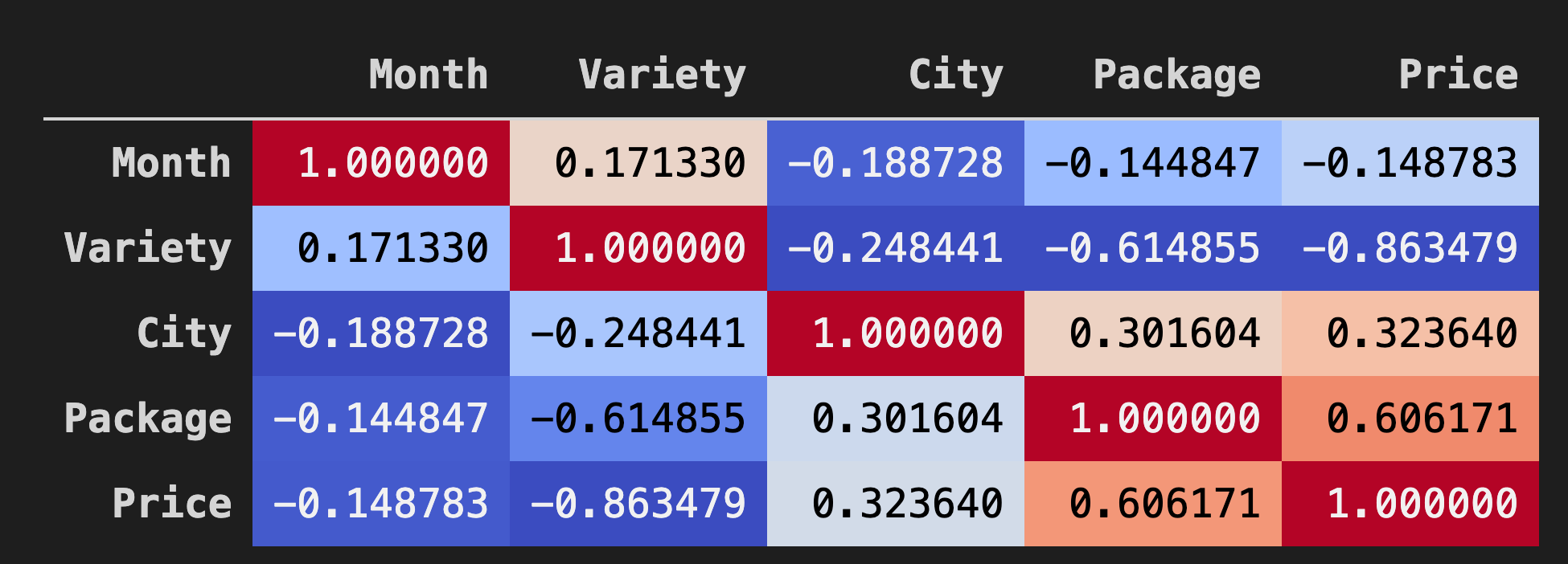
Un buon modo per visualizzare le correlazioni tra i dati nei dataframe è visualizzarli in un grafico "coolwarm":

Si usa il metodo Background_gradient() con coolwarm come valore dell'argomento:
```
corr = poly_pumpkins.corr()
corr.style.background_gradient(cmap='coolwarm')
```
Questo codice crea una mappa di calore:

Guardando questo grafico, si può visualizzare la buona correlazione tra Pacchetto e Prezzo. Quindi si dovrebbe essere in grado di creare un modello un po' migliore dell'ultimo.

Creare una pipeline

Scikit-learn include un'API utile per la creazione di modelli di regressione polinomiale: l'API make_pipeline. Viene creata una 'pipeline' che è una catena di stimatori. In questo caso, la pipeline include caratteristiche polinomiali o previsioni che formano un percorso non lineare.

Si costruiscono le colonne X e y:

X=poly_pumpkins.iloc[:,3:4].values
y=poly_pumpkins.iloc[:,4:5].values

Si crea la pipeline chiamando il metodo make_pipeline() :

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

pipeline = make_pipeline(PolynomialFeatures(4), LinearRegression())

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

pipeline.fit(np.array(X_train), y_train)

y_pred=pipeline.predict(X_test)

Creare una sequenza

A questo punto, è necessario creare un nuovo dataframe con dati ordinati in modo che la pipeline possa creare una sequenza.

Si aggiunge il seguente codice:

df = pd.DataFrame({'x': X_test[:,0], 'y': y_pred[:,0]})
df.sort_values(by='x',inplace = True)
points = pd.DataFrame(df).to_numpy()

plt.plot(points[:, 0], points[:, 1],color="blue", linewidth=3)
plt.xlabel('Package')
plt.ylabel('Price')
plt.scatter(X,y, color="black")
plt.show()

Si è creato un nuovo dataframe chiamato pd.DataFrame. Quindi si sono ordinati i valori chiamando sort_values(). Alla fine si è creato un grafico polinomiale:

Si può vedere una linea curva che si adatta meglio ai dati.

Si verifica la precisione del modello:

accuracy_score = pipeline.score(X_train,y_train)
print('Model Accuracy: ', accuracy_score)

E voilà!

Model Accuracy:  0.8537946517073784

Ecco, meglio! Si prova a prevedere un prezzo:

Fare una previsione

E possibile inserire un nuovo valore e ottenere una previsione?

Si chiami predict() per fare una previsione:

pipeline.predict( np.array([ [2.75] ]) )

Viene data questa previsione:

array([[46.34509342]])

Ha senso, visto il tracciato! Se questo è un modello migliore del precedente, guardando gli stessi dati, si deve preventivare queste zucche più costose!

Ben fatto! Sono stati creati due modelli di regressione in una lezione. Nella sezione finale sulla regressione, si imparerà a conoscere la regressione logistica per determinare le categorie.

🚀 Sfida

Testare diverse variabili in questo notebook per vedere come la correlazione corrisponde all'accuratezza del modello.

Quiz post-lezione

Revisione e Auto Apprendimento

In questa lezione si è appreso della regressione lineare. Esistono altri tipi importanti di regressione. Leggere le tecniche Stepwise, Ridge, Lazo ed Elasticnet. Un buon corso per studiare per saperne di più è il corso Stanford Statistical Learning

Compito

Costruire un modello

15 KiB Raw Blame History Unescape Escape