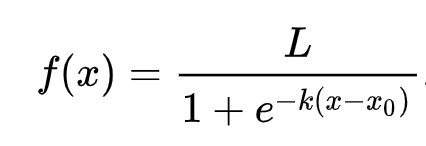19 KiB

Raw Permalink Blame History Unescape Escape

使用逻辑回归预测类别

课前测验

本课程也提供 R 版本！

简介

在本课程中，我们将学习逻辑回归，这是经典机器学习技术之一。你可以使用这种技术发现模式以预测二元类别。例如，这颗糖果是巧克力还是不是巧克力？这种疾病是否具有传染性？这个顾客会选择这个产品还是不会？

在本课程中，你将学习：

一个新的数据可视化库
逻辑回归的技术

✅ 在这个学习模块中深入了解如何使用这种回归方法。

前置知识

通过之前的南瓜数据集练习，我们已经足够熟悉它，并意识到其中有一个可以处理的二元类别：Color。

让我们构建一个逻辑回归模型来预测给定一些变量时，某个南瓜可能的颜色（橙色 🎃 或白色 👻）。

为什么在回归课程中讨论二元分类？仅仅是为了语言上的方便，因为逻辑回归实际上是一种分类方法，尽管它是基于线性的。在下一组课程中，你将学习其他分类数据的方法。

定义问题

对于我们的目的，我们将问题表达为一个二元类别：“白色”或“非白色”。数据集中还有一个“条纹”类别，但实例较少，因此我们不会使用它。实际上，在移除数据集中的空值后，它也会消失。

🎃 有趣的事实：我们有时称白色南瓜为“幽灵”南瓜。它们不太容易雕刻，因此不像橙色南瓜那么受欢迎，但它们看起来很酷！所以我们也可以将问题重新表述为：“幽灵”或“非幽灵”。👻

关于逻辑回归

逻辑回归与之前学习的线性回归有几个重要的不同点。

🎥 点击上方图片观看关于逻辑回归的简短视频概述。

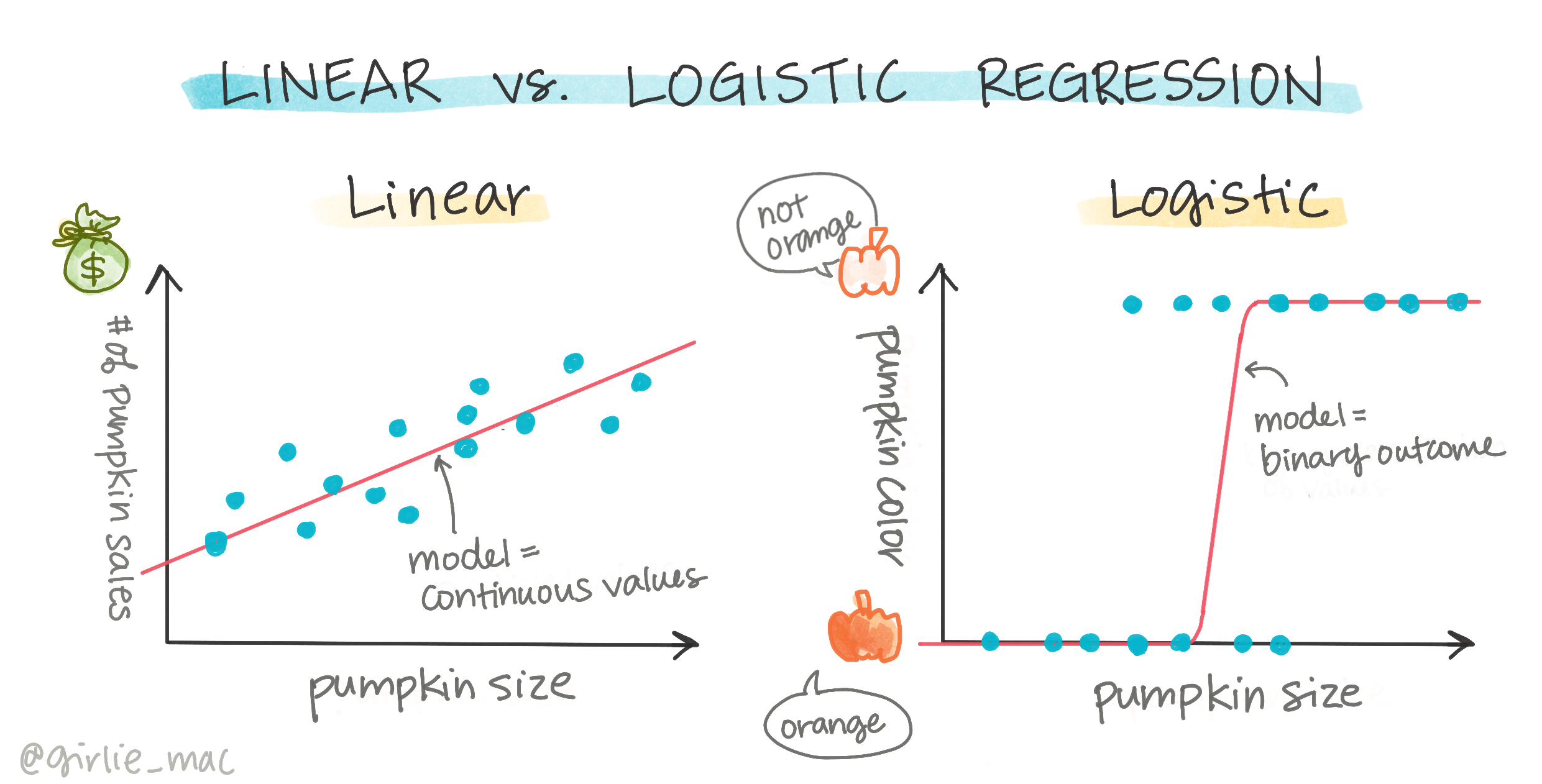
二元分类

逻辑回归与线性回归的功能不同。前者预测二元类别（例如“白色或非白色”），而后者能够预测连续值，例如根据南瓜的产地和收获时间，价格将上涨多少。

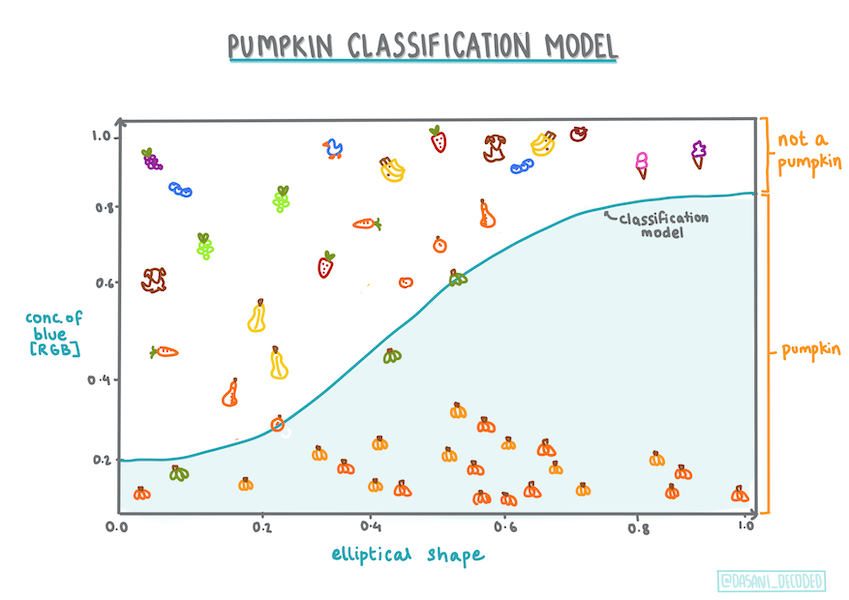
信息图由 Dasani Madipalli 提供

其他分类

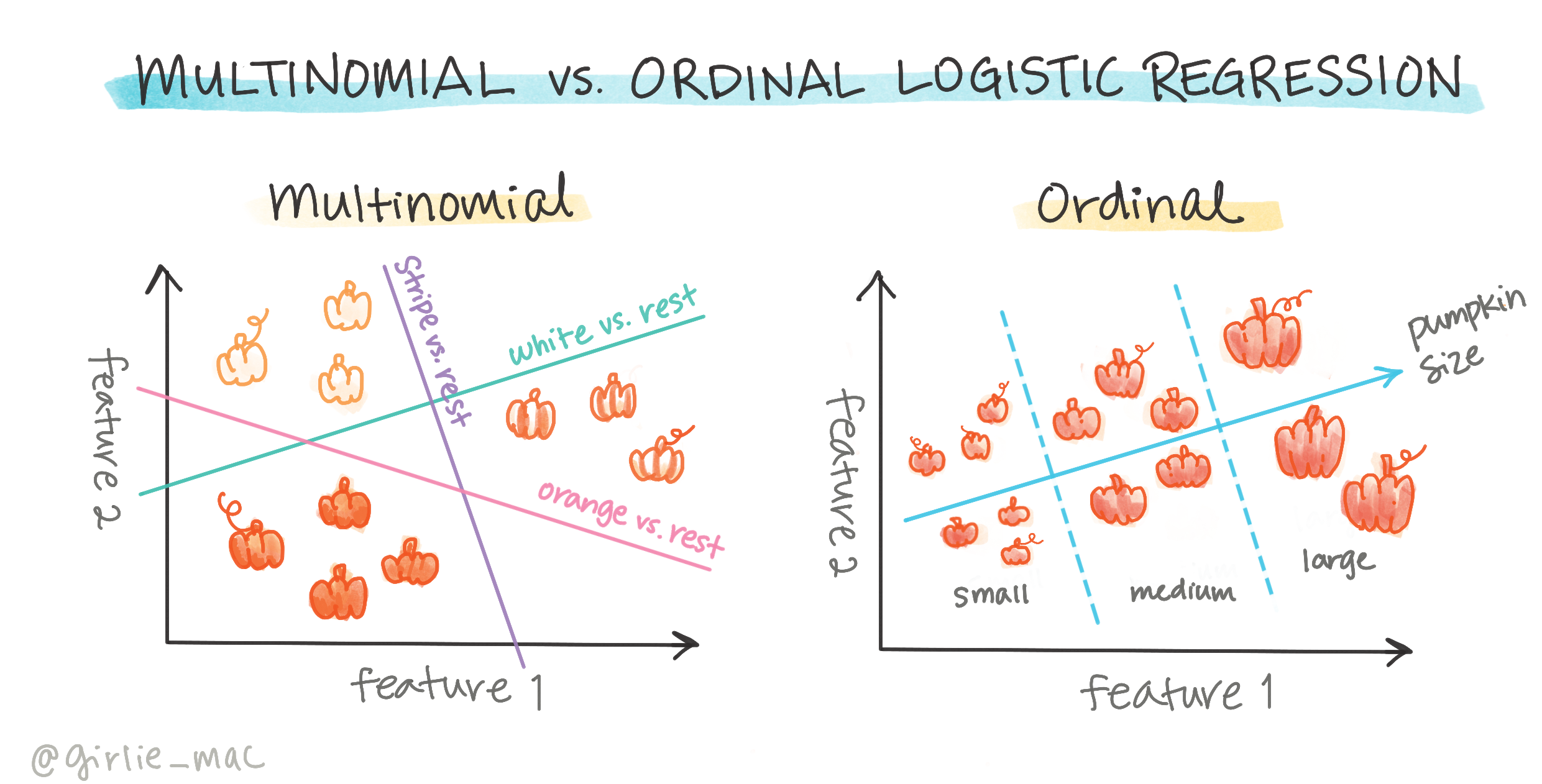
逻辑回归还有其他类型，包括多项式和有序分类：

多项式分类：涉及多个类别，例如“橙色、白色和条纹”。
有序分类：涉及有序类别，适用于逻辑排序的结果，例如按有限大小排序的南瓜（迷你、小、中、大、特大、超大）。

变量不需要相关

还记得线性回归在变量相关性较高时效果更好吗？逻辑回归正好相反——变量不需要相关性。这适用于数据中相关性较弱的情况。

需要大量干净数据

逻辑回归在使用更多数据时会给出更准确的结果；我们的数据集较小，因此并不理想。

🎥 点击上方图片观看关于准备线性回归数据的简短视频概述。

✅ 思考哪些类型的数据适合逻辑回归。

练习 - 整理数据

首先，清理数据，删除空值并选择部分列：

添加以下代码：


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

你可以随时查看新的数据框：

pumpkins.info

可视化 - 分类图

现在你已经加载了起始笔记本，其中包含南瓜数据，并清理了数据以保留一些变量，包括 Color。让我们使用一个不同的库 Seaborn 在笔记本中可视化数据框。Seaborn 是基于我们之前使用的 Matplotlib 构建的。

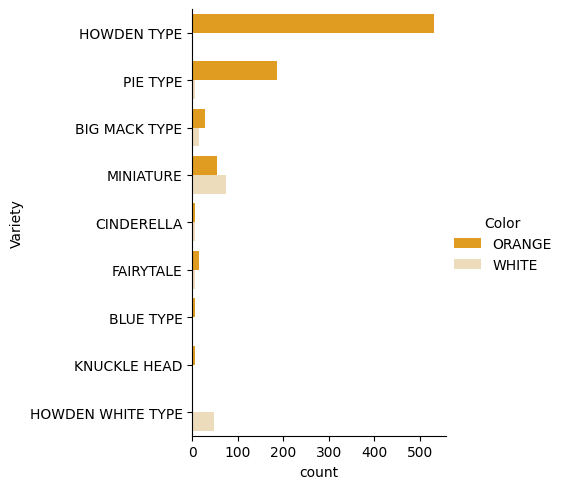
Seaborn 提供了一些很棒的方式来可视化数据。例如，你可以在分类图中比较 Variety 和 Color 数据的分布。

使用 catplot 函数创建这样的图，使用南瓜数据 pumpkins，并为每个南瓜类别（橙色或白色）指定颜色映射：
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
通过观察数据，你可以看到 Color 数据与 Variety 的关系。

✅ 根据这个分类图，你能想到哪些有趣的探索？

数据预处理：特征和标签编码

我们的南瓜数据集的所有列都包含字符串值。处理分类数据对人类来说很直观，但对机器来说却不然。机器学习算法更适合处理数字数据。这就是为什么编码是数据预处理阶段非常重要的一步，它使我们能够将分类数据转换为数值数据，而不会丢失任何信息。良好的编码有助于构建良好的模型。

对于特征编码，主要有两种编码器：

有序编码器：适用于有序变量，即数据具有逻辑顺序的分类变量，例如数据集中的 Item Size 列。它创建一个映射，使每个类别由一个数字表示，该数字是列中类别的顺序。

from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)

分类编码器：适用于无序变量，即数据没有逻辑顺序的分类变量，例如数据集中除 Item Size 之外的所有特征。它是一种独热编码，这意味着每个类别由一个二进制列表示：如果南瓜属于该类别，则编码变量为 1，否则为 0。
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

然后，使用 ColumnTransformer 将多个编码器合并为一个步骤，并将其应用于适当的列。

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

另一方面，为了编码标签，我们使用 scikit-learn 的 LabelEncoder 类，这是一个实用类，用于将标签标准化，使其仅包含 0 到 n_classes-1（这里是 0 和 1）之间的值。

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

完成特征和标签编码后，我们可以将它们合并为一个新的数据框 encoded_pumpkins。

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ 使用有序编码器处理 Item Size 列有哪些优势？

分析变量之间的关系

现在我们已经对数据进行了预处理，可以分析特征和标签之间的关系，以了解模型在给定特征的情况下预测标签的能力。

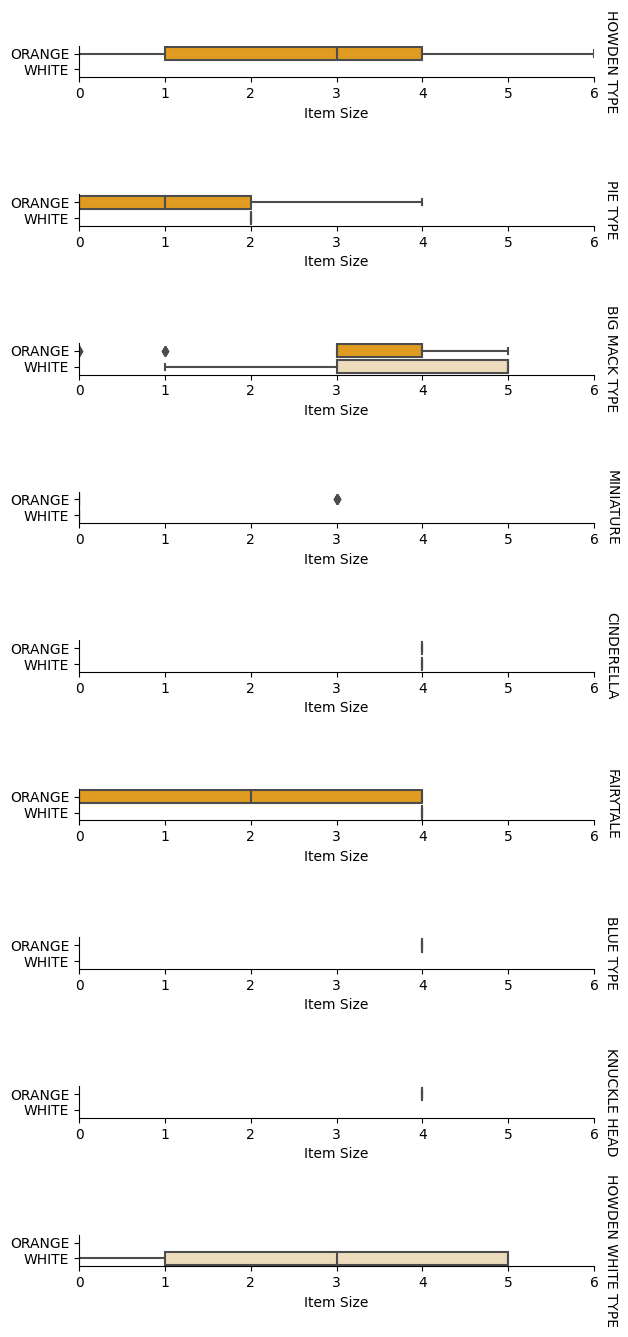
分析这种关系的最佳方式是绘制数据。我们将再次使用 Seaborn 的 catplot 函数，以分类图的形式可视化 Item Size、Variety 和 Color 之间的关系。为了更好地绘制数据，我们将使用编码后的 Item Size 列和未编码的 Variety 列。

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

使用蜂群图

由于 Color 是一个二元类别（白色或非白色），它需要“一种专门的方法来可视化”。还有其他方法可以可视化此类别与其他变量的关系。

你可以使用 Seaborn 图表并排可视化变量。

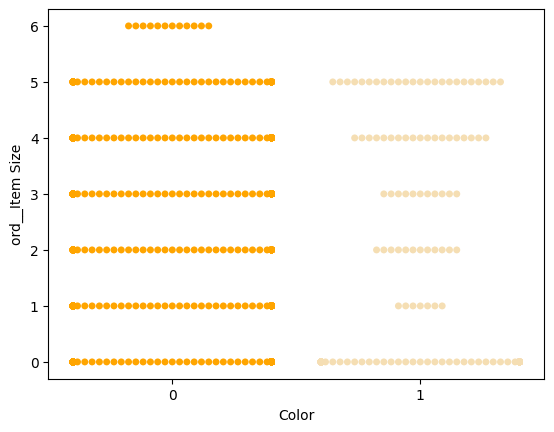
尝试使用“蜂群图”来显示值的分布：

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

注意：上述代码可能会生成警告，因为 Seaborn 无法在蜂群图中表示如此多的数据点。一个可能的解决方案是通过使用 size 参数减小标记的大小。然而，请注意，这会影响图表的可读性。

🧮 数学原理

逻辑回归依赖于“最大似然”概念，使用Sigmoid 函数。在图表上，Sigmoid 函数看起来像一个“S”形。它将一个值映射到 0 和 1 之间的某个位置。它的曲线也被称为“逻辑曲线”。其公式如下：

其中，Sigmoid 的中点位于 x 的 0 点，L 是曲线的最大值，k 是曲线的陡度。如果函数的结果大于 0.5，则该标签将被归类为二元选择中的“1”。否则，将被归类为“0”。

构建模型

在 Scikit-learn 中构建一个用于二元分类的模型非常简单。

🎥 点击上方图片观看关于构建线性回归模型的简短视频概述。

选择你想在分类模型中使用的变量，并调用 train_test_split() 分割训练集和测试集：

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

现在你可以通过调用 fit() 使用训练数据训练模型，并打印结果：

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

查看模型的评分。考虑到数据只有大约 1000 行，结果还不错：

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

使用混淆矩阵更好地理解模型

虽然你可以通过打印上述项获得评分报告术语，但使用混淆矩阵可能更容易理解模型的表现。

🎓 “混淆矩阵”（或“误差矩阵”）是一个表格，用于表达模型的真实与预测的正负情况，从而评估预测的准确性。

要使用混淆矩阵，调用 confusion_matrix()：

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

查看模型的混淆矩阵：

array([[162,   4],
       [ 11,  22]])

在 Scikit-learn 中，混淆矩阵的行（轴 0）是实际标签，列（轴 1）是预测标签。

	0	1
0	TN	FP
1	FN	TP

这里发生了什么？假设我们的模型被要求在两个二元类别之间对南瓜进行分类，“白色”和“非白色”。

如果模型预测南瓜为非白色，而实际上属于“非白色”类别，我们称之为真负（True Negative），显示在左上角。
如果模型预测南瓜为白色，而实际上属于“非白色”类别，我们称之为假负（False Negative），显示在左下角。
如果模型预测南瓜为非白色，而实际上属于“白色”类别，我们称之为假正（False Positive），显示在右上角。
如果模型预测南瓜为白色，而实际上属于“白色”类别，我们称之为真正（True Positive），显示在右下角。

正如你可能猜到的，较多的真正和真负以及较少的假正和假负表明模型表现更好。混淆矩阵如何与精确率和召回率相关联？请记住，上面打印的分类报告显示精确率为 0.85，召回率为 0.67。

精确率 = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

召回率 = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ 问：根据混淆矩阵，模型表现如何？
答：还不错；有相当多的真正例，但也有一些假负例。

让我们通过混淆矩阵中 TP/TN 和 FP/FN 的映射，重新回顾之前提到的术语：

🎓 精确率（Precision）：TP/(TP + FP)
检索到的实例中，相关实例的比例（例如，哪些标签被正确标记）。

🎓 召回率（Recall）：TP/(TP + FN)
相关实例中被检索到的比例，无论是否被正确标记。

🎓 F1 分数（f1-score）：(2 * precision * recall)/(precision + recall)
精确率和召回率的加权平均值，最佳值为 1，最差值为 0。

🎓 支持度（Support）：
每个标签被检索到的次数。

🎓 准确率（Accuracy）：(TP + TN)/(TP + TN + FP + FN)
样本中标签被正确预测的百分比。

🎓 宏平均（Macro Avg）：
对每个标签的指标进行无权重平均的计算，不考虑标签的不平衡。

🎓 加权平均（Weighted Avg）：
对每个标签的指标进行加权平均的计算，权重由支持度（每个标签的真实实例数）决定。

✅ 你能想到如果想减少假负例的数量，应该关注哪个指标吗？

可视化该模型的 ROC 曲线

🎥 点击上方图片观看关于 ROC 曲线的简短视频概述

让我们再做一个可视化，看看所谓的“ROC”曲线：

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
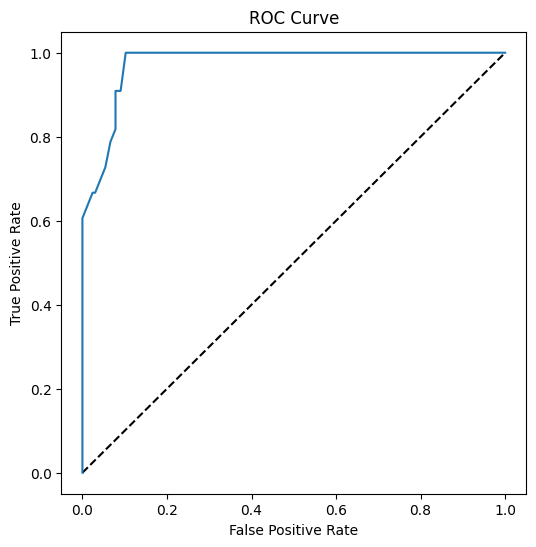
plt.show()

使用 Matplotlib 绘制模型的接收者操作特性曲线（ROC）。ROC 曲线通常用于查看分类器输出的真阳性与假阳性之间的关系。“ROC 曲线通常以真阳性率为 Y 轴，假阳性率为 X 轴。”因此，曲线的陡峭程度以及曲线与中线之间的空间很重要：你希望曲线迅速向上并越过中线。在我们的例子中，起初有一些假阳性，然后曲线正确地向上并越过中线：

最后，使用 Scikit-learn 的 roc_auc_score API 计算实际的“曲线下面积”（AUC）：

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

结果是 0.9749908725812341。由于 AUC 的范围是 0 到 1，你希望分数越大越好，因为一个 100% 正确预测的模型的 AUC 为 1；在这种情况下，该模型表现“相当不错”。

在未来的分类课程中，你将学习如何迭代以提高模型的分数。但现在，恭喜你！你已经完成了这些回归课程！

🚀挑战

关于逻辑回归还有很多内容可以深入探讨！但最好的学习方式是动手实践。找到一个适合这种分析的数据集，并用它构建一个模型。你学到了什么？提示：试试 Kaggle 上的一些有趣数据集。

课后测验

复习与自学

阅读斯坦福大学的这篇论文的前几页，了解逻辑回归的一些实际应用。思考哪些任务更适合我们到目前为止学习的回归类型。哪种方法效果更好？

作业

重试这个回归任务

免责声明：
本文档使用AI翻译服务Co-op Translator进行翻译。尽管我们努力确保准确性，但请注意，自动翻译可能包含错误或不准确之处。应以原始语言的文档作为权威来源。对于关键信息，建议使用专业人工翻译。对于因使用本翻译而引起的任何误解或误读，我们概不负责。

19 KiB Raw Permalink Blame History Unescape Escape