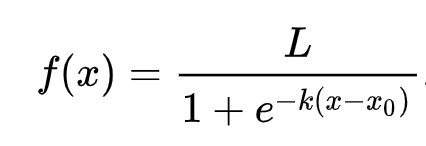32 KiB

Raw Permalink Blame History Unescape Escape

Логістична регресія для прогнозування категорій

Тест перед лекцією

Цей урок доступний у R!

Вступ

У цьому останньому уроці про регресію, одну з базових класичних технік машинного навчання, ми розглянемо логістичну регресію. Цю техніку можна використовувати для виявлення закономірностей і прогнозування бінарних категорій. Чи є ця цукерка шоколадом чи ні? Чи є ця хвороба заразною чи ні? Чи вибере цей клієнт продукт чи ні?

У цьому уроці ви дізнаєтесь:

Нову бібліотеку для візуалізації даних
Техніки логістичної регресії

✅ Поглибте своє розуміння роботи з цим типом регресії у модулі навчання

Передумови

Працюючи з даними про гарбузи, ми вже достатньо знайомі з ними, щоб зрозуміти, що є одна бінарна категорія, з якою ми можемо працювати: Color.

Давайте побудуємо модель логістичної регресії, щоб прогнозувати, якого кольору, ймовірно, буде даний гарбуз (помаранчевий 🎃 чи білий 👻), враховуючи деякі змінні.

Чому ми говоримо про бінарну класифікацію в уроці про регресію? Лише для мовної зручності, оскільки логістична регресія насправді є методом класифікації, хоча й базується на лінійній моделі. Дізнайтеся про інші способи класифікації даних у наступній групі уроків.

Визначення питання

Для наших цілей ми сформулюємо це як бінарне: "Білий" чи "Не білий". У нашому наборі даних також є категорія "смугастий", але випадків її використання мало, тому ми її не враховуватимемо. Вона зникає після видалення нульових значень із набору даних.

🎃 Цікавий факт: ми іноді називаємо білі гарбузи "гарбузами-привидами". Їх не дуже легко вирізати, тому вони не такі популярні, як помаранчеві, але виглядають круто! Тож ми також могли б переформулювати наше питання як: "Привид" чи "Не привид". 👻

Про логістичну регресію

Логістична регресія відрізняється від лінійної регресії, яку ви вивчали раніше, кількома важливими аспектами.

🎥 Натисніть на зображення вище, щоб переглянути коротке відео про логістичну регресію.

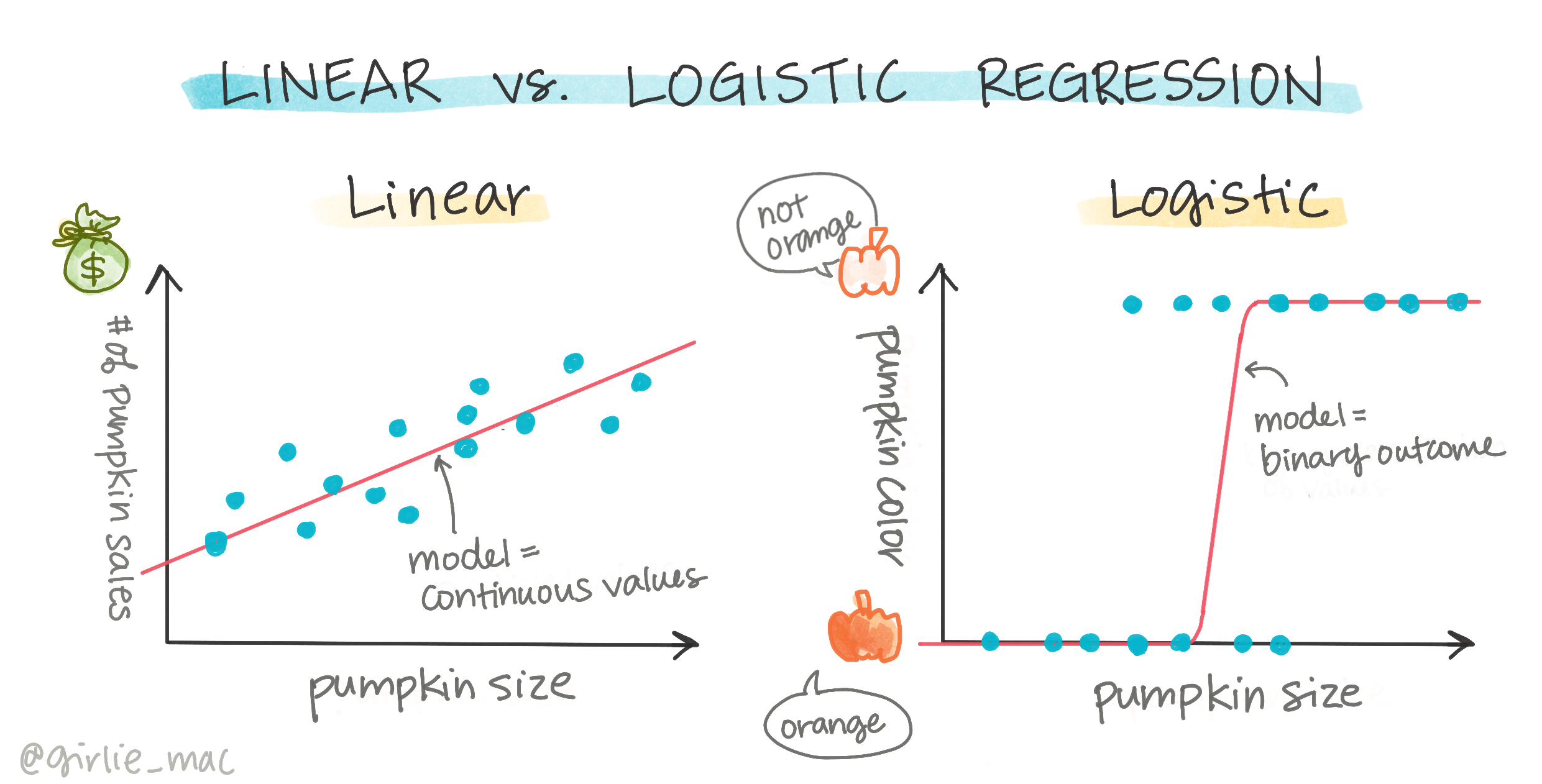
Бінарна класифікація

Логістична регресія не пропонує тих самих функцій, що й лінійна регресія. Перша пропонує прогнозування бінарної категорії ("білий чи не білий"), тоді як друга здатна прогнозувати безперервні значення, наприклад, враховуючи походження гарбуза та час збору врожаю, наскільки зросте його ціна.

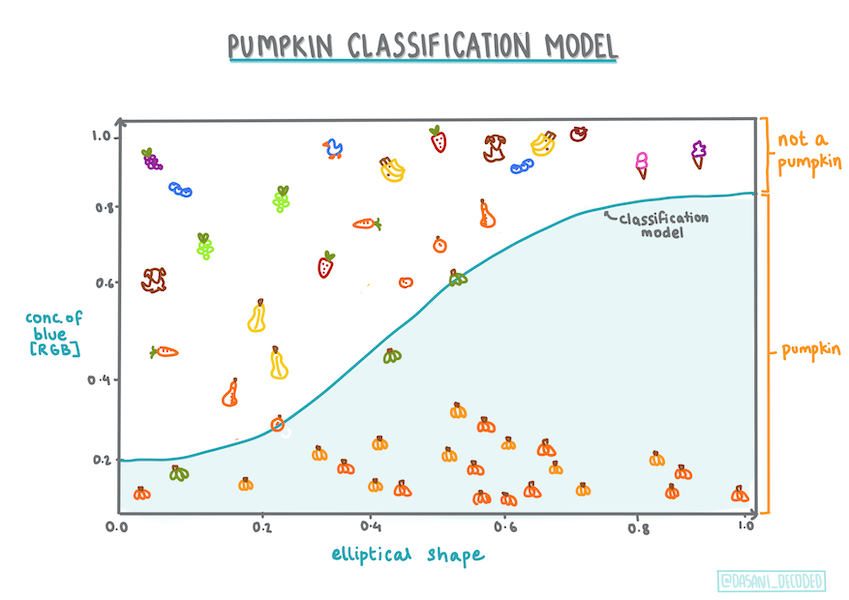
Інфографіка від Dasani Madipalli

Інші класифікації

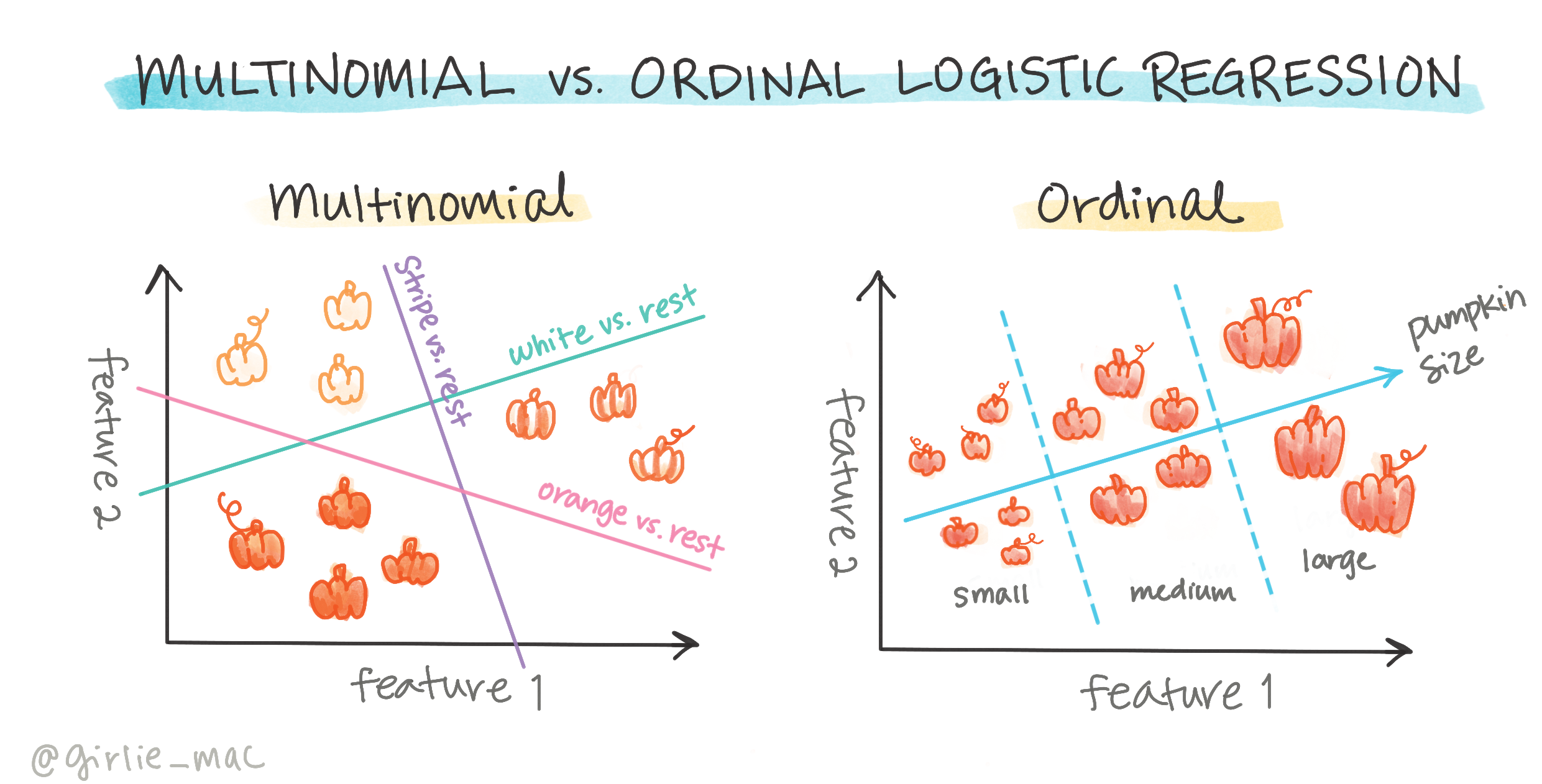
Існують інші типи логістичної регресії, включаючи мультиноміальну та порядкову:

Мультиноміальна, яка передбачає наявність більше ніж однієї категорії - "Помаранчевий, Білий і Смугастий".
Порядкова, яка передбачає впорядковані категорії, корисна, якщо ми хочемо впорядкувати результати логічно, наприклад, гарбузи, які впорядковані за обмеженою кількістю розмірів (mini, sm, med, lg, xl, xxl).

Змінні НЕ повинні корелювати

Пам'ятаєте, як лінійна регресія працювала краще з більш корельованими змінними? Логістична регресія є протилежною - змінні не повинні співпадати. Це підходить для даних, які мають слабкі кореляції.

Вам потрібні великі обсяги чистих даних

Логістична регресія дає більш точні результати, якщо використовувати більше даних; наш невеликий набір даних не є оптимальним для цього завдання, тому враховуйте це.

✅ Подумайте про типи даних, які добре підходять для логістичної регресії

Вправа - підготовка даних

Спочатку трохи очистимо дані, видаливши нульові значення та вибравши лише деякі стовпці:

Додайте наступний код:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Ви завжди можете переглянути ваш новий датафрейм:

pumpkins.info

Візуалізація - категоріальний графік

На даний момент ви завантажили початковий ноутбук з даними про гарбузи та очистили його, щоб зберегти набір даних, що містить кілька змінних, включаючи Color. Давайте візуалізуємо датафрейм у ноутбуці, використовуючи іншу бібліотеку: Seaborn, яка побудована на Matplotlib, яку ми використовували раніше.

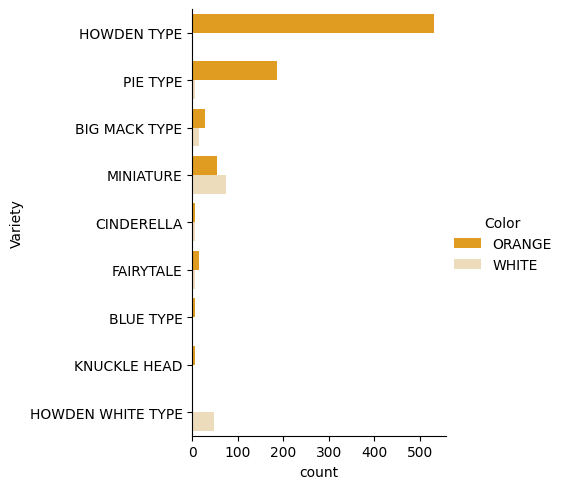
Seaborn пропонує цікаві способи візуалізації ваших даних. Наприклад, ви можете порівняти розподіли даних для кожного Variety і Color у категоріальному графіку.

Створіть такий графік, використовуючи функцію catplot, дані про гарбузи pumpkins і вказавши кольорове відображення для кожної категорії гарбузів (помаранчевий або білий):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Спостерігаючи за даними, ви можете побачити, як дані про Color співвідносяться з Variety.

✅ Враховуючи цей категоріальний графік, які цікаві дослідження ви можете уявити?

Попередня обробка даних: кодування ознак і міток

Наш набір даних про гарбузи містить текстові значення для всіх своїх стовпців. Робота з категоріальними даними є інтуїтивною для людей, але не для машин. Алгоритми машинного навчання добре працюють із числами. Саме тому кодування є дуже важливим етапом у фазі попередньої обробки даних, оскільки воно дозволяє перетворити категоріальні дані в числові, не втрачаючи жодної інформації. Хороше кодування сприяє створенню хорошої моделі.

Для кодування ознак існує два основних типи кодерів:

Ordinal encoder: добре підходить для порядкових змінних, які є категоріальними змінними, де їх дані мають логічний порядок, як стовпець Item Size у нашому наборі даних. Він створює відображення, так що кожна категорія представлена числом, яке є порядком категорії в стовпці.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Categorical encoder: добре підходить для номінальних змінних, які є категоріальними змінними, де їх дані не мають логічного порядку, як усі ознаки, відмінні від Item Size у нашому наборі даних. Це кодування "один-гарячий", що означає, що кожна категорія представлена бінарним стовпцем: закодована змінна дорівнює 1, якщо гарбуз належить до цієї Variety, і 0 в іншому випадку.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Потім ColumnTransformer використовується для об'єднання кількох кодерів в один етап і застосування їх до відповідних стовпців.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Для кодування мітки ми використовуємо клас LabelEncoder з бібліотеки scikit-learn, який є утилітою для нормалізації міток так, щоб вони містили лише значення між 0 і n_classes-1 (тут, 0 і 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Після того, як ми закодували ознаки та мітку, ми можемо об'єднати їх у новий датафрейм encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Які переваги використання порядкового кодера для стовпця Item Size?

Аналіз взаємозв'язків між змінними

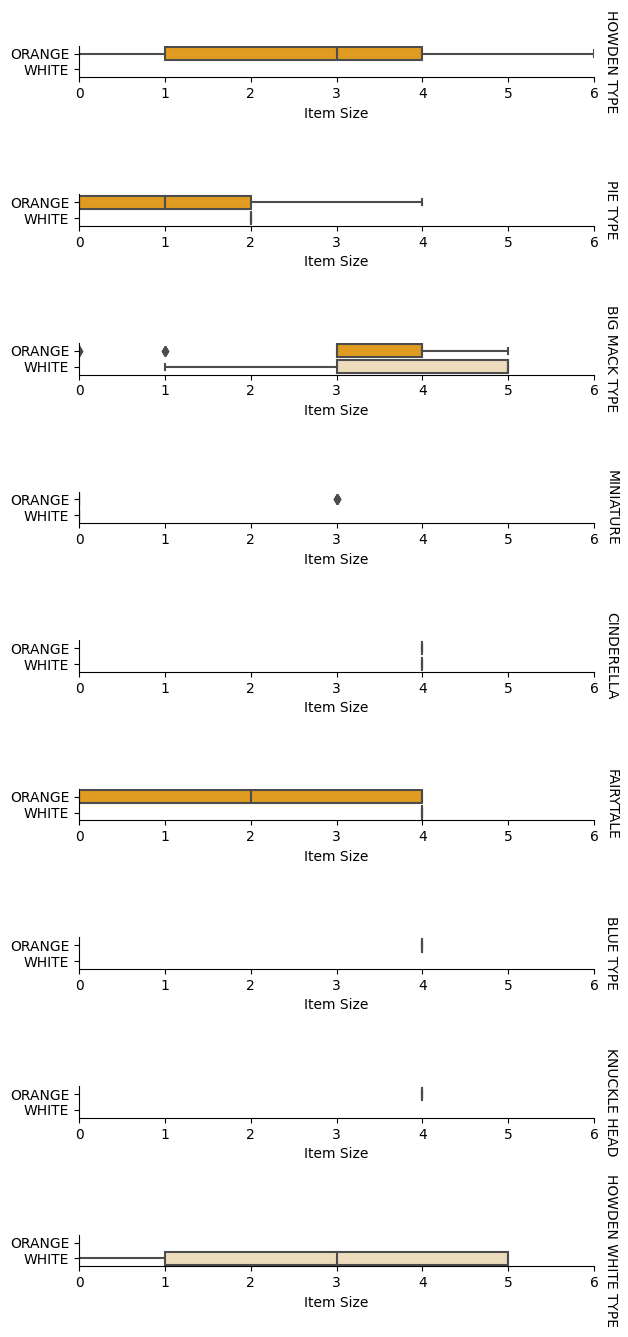
Тепер, коли ми попередньо обробили наші дані, ми можемо аналізувати взаємозв'язки між ознаками та міткою, щоб зрозуміти, наскільки добре модель зможе прогнозувати мітку, враховуючи ознаки. Найкращий спосіб виконати такий аналіз - це побудова графіків. Ми знову будемо використовувати функцію catplot з бібліотеки Seaborn, щоб візуалізувати взаємозв'язки між Item Size, Variety і Color у категоріальному графіку. Для кращої побудови графіка ми будемо використовувати закодований стовпець Item Size і незакодований стовпець Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Використання swarm plot

Оскільки Color є бінарною категорією (Білий чи Не білий), для її візуалізації потрібен 'спеціалізований підхід'. Існують інші способи візуалізації взаємозв'язку цієї категорії з іншими змінними.

Ви можете візуалізувати змінні поруч за допомогою графіків Seaborn.

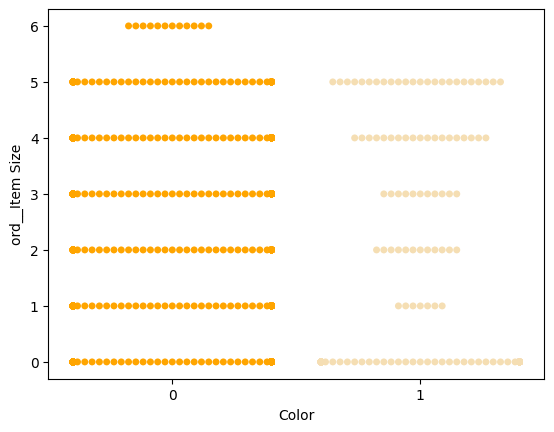
Спробуйте побудувати графік типу 'swarm', щоб показати розподіл значень:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Зверніть увагу: код вище може викликати попередження, оскільки Seaborn не може представити таку кількість точок даних у swarm графіку. Можливим рішенням є зменшення розміру маркера, використовуючи параметр 'size'. Однак майте на увазі, що це впливає на читабельність графіка.

🧮 Покажіть мені математику

Логістична регресія базується на концепції 'максимальної ймовірності', використовуючи сигмоїдальні функції. 'Сигмоїдальна функція' на графіку виглядає як форма 'S'. Вона бере значення і відображає його в діапазоні між 0 і 1. Її крива також називається 'логістичною кривою'. Її формула виглядає так:

де середина сигмоїди знаходиться на точці 0 для x, L - максимальне значення кривої, а k - крутизна кривої. Якщо результат функції більше 0.5, мітка буде віднесена до класу '1' бінарного вибору. Якщо ні, вона буде класифікована як '0'.

Побудова моделі

Побудова моделі для знаходження цих бінарних класифікацій є досить простою у Scikit-learn.

🎥 Натисніть на зображення вище, щоб переглянути коротке відео про побудову моделі лінійної регресії

Виберіть змінні, які ви хочете використовувати у вашій моделі класифікації, і розділіть навчальні та тестові набори, викликавши train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Тепер ви можете навчити свою модель, викликавши fit() з вашими навчальними даними, і вивести її результат:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Подивіться на результати вашої моделі. Вони непогані, враховуючи, що у вас є лише близько 1000 рядків даних:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Краще розуміння через матрицю плутанини

Хоча ви можете отримати звіт про результати терміни, вивівши наведені вище елементи, ви можете краще зрозуміти свою модель, використовуючи матрицю плутанини, щоб допомогти нам зрозуміти, як модель працює.

🎓 'Матриця плутанини' (або 'матриця помилок') - це таблиця, яка виражає справжні та хибні позитивні та негативні результати вашої моделі, таким чином оцінюючи точність прогнозів.

Щоб використовувати матрицю плутанини, викличте confusion_matrix():
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)
```
Подивіться на матрицю плутанини вашої моделі:
```
array([[162,   4],
       [ 11,  22]])
```

У Scikit-learn рядки (вісь 0) представляють фактичні мітки, а стовпці (вісь 1) - прогнозовані мітки.

	0	1
0	TN	FP
1	FN	TP

Що тут відбувається? Припустимо, наша модель має класифікувати гарбузи між двома бінарними категоріями: категорія 'білий' і категорія 'не білий'.

Якщо ваша модель прогнозує гарбуз як не білий, і він насправді належить до категорії 'не білий', ми називаємо це справжнім негативом, показаним у верхньому лівому числі.
Якщо ваша модель прогнозує гарбуз як білий, і він насправді належить до категорії 'не білий', ми називаємо це хибним негативом, показаним у нижньому лівому числі.
Якщо ваша модель прогнозує гарбуз як не білий, і він насправді належить до категорії 'білий', ми називаємо це хибним позитив Як пов'язана матриця плутанини з точністю та повнотою? Пам'ятайте, що класифікаційний звіт, наведений вище, показав точність (0.85) і повноту (0.67).

Точність = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Повнота = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ Питання: Як, згідно з матрицею плутанини, впорався модель? Відповідь: Непогано; є значна кількість правильних негативних результатів, але також кілька хибно-негативних.

Давайте ще раз розглянемо терміни, які ми бачили раніше, за допомогою відображення TP/TN і FP/FN у матриці плутанини:

🎓 Точність: TP/(TP + FP) Частка релевантних прикладів серед отриманих (наприклад, які мітки були правильно позначені).

🎓 Повнота: TP/(TP + FN) Частка релевантних прикладів, які були отримані, незалежно від того, чи були вони правильно позначені.

🎓 f1-оцінка: (2 * точність * повнота)/(точність + повнота) Зважене середнє точності та повноти, де найкраще значення — 1, а найгірше — 0.

🎓 Підтримка: Кількість випадків кожної мітки, що були отримані.

🎓 Точність (Accuracy): (TP + TN)/(TP + TN + FP + FN) Відсоток міток, які були правильно передбачені для вибірки.

🎓 Середнє значення (Macro Avg): Розрахунок незваженого середнього значення метрик для кожної мітки, без урахування дисбалансу міток.

🎓 Зважене середнє (Weighted Avg): Розрахунок середнього значення метрик для кожної мітки з урахуванням дисбалансу міток шляхом зважування їх за підтримкою (кількість правильних випадків для кожної мітки).

✅ Чи можете ви визначити, на яку метрику слід звертати увагу, якщо ви хочете, щоб ваша модель зменшила кількість хибно-негативних результатів?

Візуалізація ROC-кривої цієї моделі

🎥 Натисніть на зображення вище, щоб переглянути короткий відеоогляд ROC-кривих.

Давайте зробимо ще одну візуалізацію, щоб побачити так звану 'ROC'-криву:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

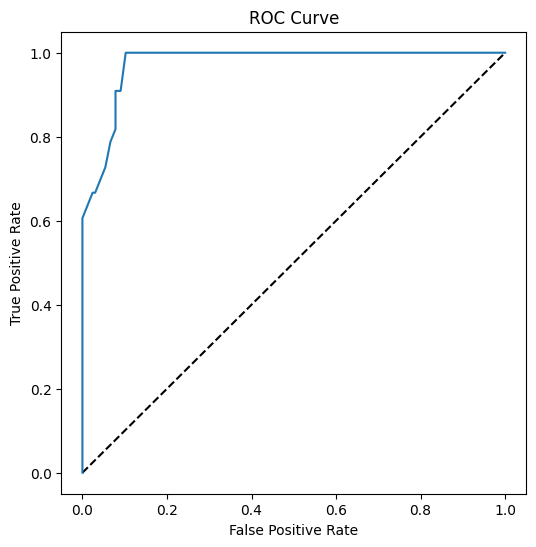
За допомогою Matplotlib побудуйте Receiving Operating Characteristic або ROC-криву моделі. ROC-криві часто використовуються для оцінки результатів класифікатора з точки зору його істинно позитивних і хибно позитивних результатів. "ROC-криві зазвичай мають істинно позитивну частоту на осі Y і хибно позитивну частоту на осі X." Таким чином, важливі крутизна кривої та простір між середньою лінією і кривою: ви хочете, щоб крива швидко піднімалася вгору і відходила від лінії. У нашому випадку є хибно позитивні результати на початку, а потім лінія піднімається вгору і відходить належним чином:

Нарешті, скористайтеся roc_auc_score API з бібліотеки Scikit-learn, щоб обчислити фактичну 'Площу під кривою' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Результат становить 0.9749908725812341. Оскільки AUC варіюється від 0 до 1, вам потрібен високий показник, адже модель, яка на 100% правильно передбачає результати, матиме AUC, що дорівнює 1; у цьому випадку модель доволі хороша.

У майбутніх уроках з класифікації ви дізнаєтеся, як ітеративно покращувати показники вашої моделі. Але наразі вітаємо! Ви завершили ці уроки з регресії!

🚀Виклик

Логістична регресія має ще багато цікавого! Але найкращий спосіб навчитися — це експериментувати. Знайдіть набір даних, який підходить для такого типу аналізу, і створіть модель на його основі. Що ви дізналися? Порада: спробуйте Kaggle для пошуку цікавих наборів даних.

Тест після лекції

Огляд і самостійне навчання

Прочитайте перші кілька сторінок цієї статті зі Стенфорда про деякі практичні застосування логістичної регресії. Подумайте про завдання, які краще підходять для одного чи іншого типу регресії, які ми вивчали до цього моменту. Що працюватиме найкраще?

Завдання

Повторення цієї регресії

Відмова від відповідальності:
Цей документ було перекладено за допомогою сервісу автоматичного перекладу Co-op Translator. Хоча ми прагнемо до точності, зверніть увагу, що автоматичні переклади можуть містити помилки або неточності. Оригінальний документ мовою оригіналу слід вважати авторитетним джерелом. Для критично важливої інформації рекомендується професійний людський переклад. Ми не несемо відповідальності за будь-які непорозуміння або неправильні тлумачення, що виникли внаслідок використання цього перекладу.

32 KiB Raw Permalink Blame History Unescape Escape