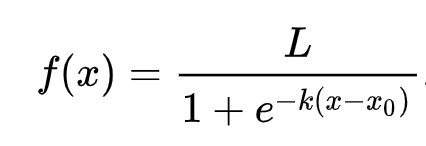23 KiB

Raw Permalink Blame History Unescape Escape

Kategorileri Tahmin Etmek İçin Lojistik Regresyon

Ders Öncesi Test

Bu ders R dilinde de mevcut!

Giriş

Regresyon üzerine olan bu son derste, temel klasik ML tekniklerinden biri olan Lojistik Regresyonu inceleyeceğiz. Bu tekniği, ikili kategorileri tahmin etmek için desenler keşfetmek amacıyla kullanabilirsiniz. Bu şeker çikolata mı değil mi? Bu hastalık bulaşıcı mı değil mi? Bu müşteri bu ürünü seçer mi seçmez mi?

Bu derste şunları öğreneceksiniz:

Veri görselleştirme için yeni bir kütüphane
Lojistik regresyon teknikleri

✅ Bu tür regresyonla çalışma konusundaki bilginizi şu Öğrenme modülünde derinleştirin.

Ön Koşul

Balkabağı verisiyle çalıştıktan sonra, üzerinde çalışabileceğimiz bir ikili kategori olduğunu fark edecek kadar aşina olduk: Renk.

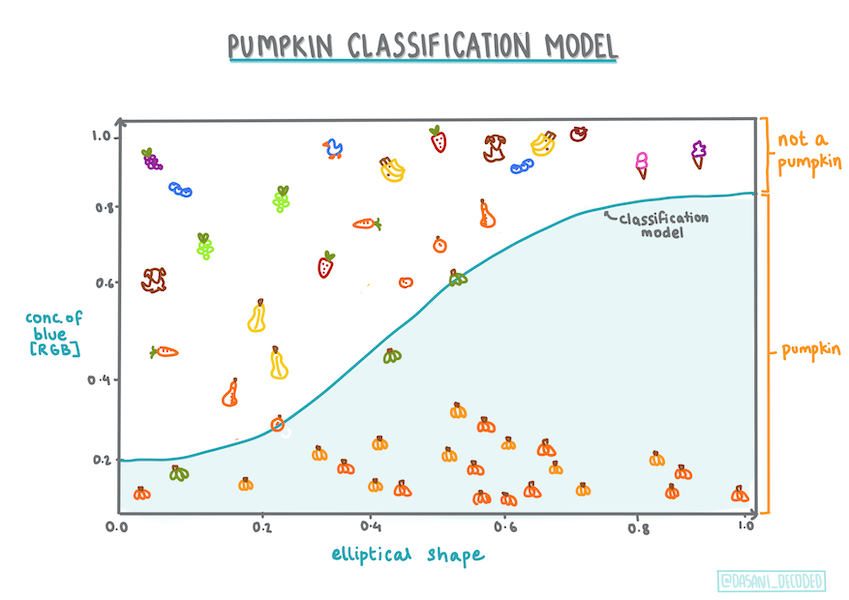
Bazı değişkenlere dayanarak, belirli bir balkabağının muhtemelen hangi renkte olacağını (turuncu 🎃 veya beyaz 👻) tahmin etmek için bir lojistik regresyon modeli oluşturalım.

Regresyonla ilgili bir ders grubunda neden ikili sınıflandırmadan bahsediyoruz? Sadece dilsel kolaylık için, çünkü lojistik regresyon aslında bir sınıflandırma yöntemi, ancak doğrusal tabanlı bir yöntemdir. Veriyi sınıflandırmanın diğer yollarını bir sonraki ders grubunda öğrenin.

Soruyu Tanımlayın

Amacımız için bunu bir ikili olarak ifade edeceğiz: 'Beyaz' veya 'Beyaz Değil'. Veri setimizde ayrıca 'çizgili' bir kategori var, ancak çok az örneği olduğu için bunu kullanmayacağız. Zaten veri setinden eksik değerleri kaldırdığımızda bu kategori kayboluyor.

🎃 Eğlenceli bilgi: Beyaz balkabaklarına bazen 'hayalet' balkabakları diyoruz. Oyması çok kolay değil, bu yüzden turuncu olanlar kadar popüler değiller ama oldukça havalı görünüyorlar! Bu yüzden sorumuzu şu şekilde de yeniden formüle edebiliriz: 'Hayalet' veya 'Hayalet Değil'. 👻

Lojistik Regresyon Hakkında

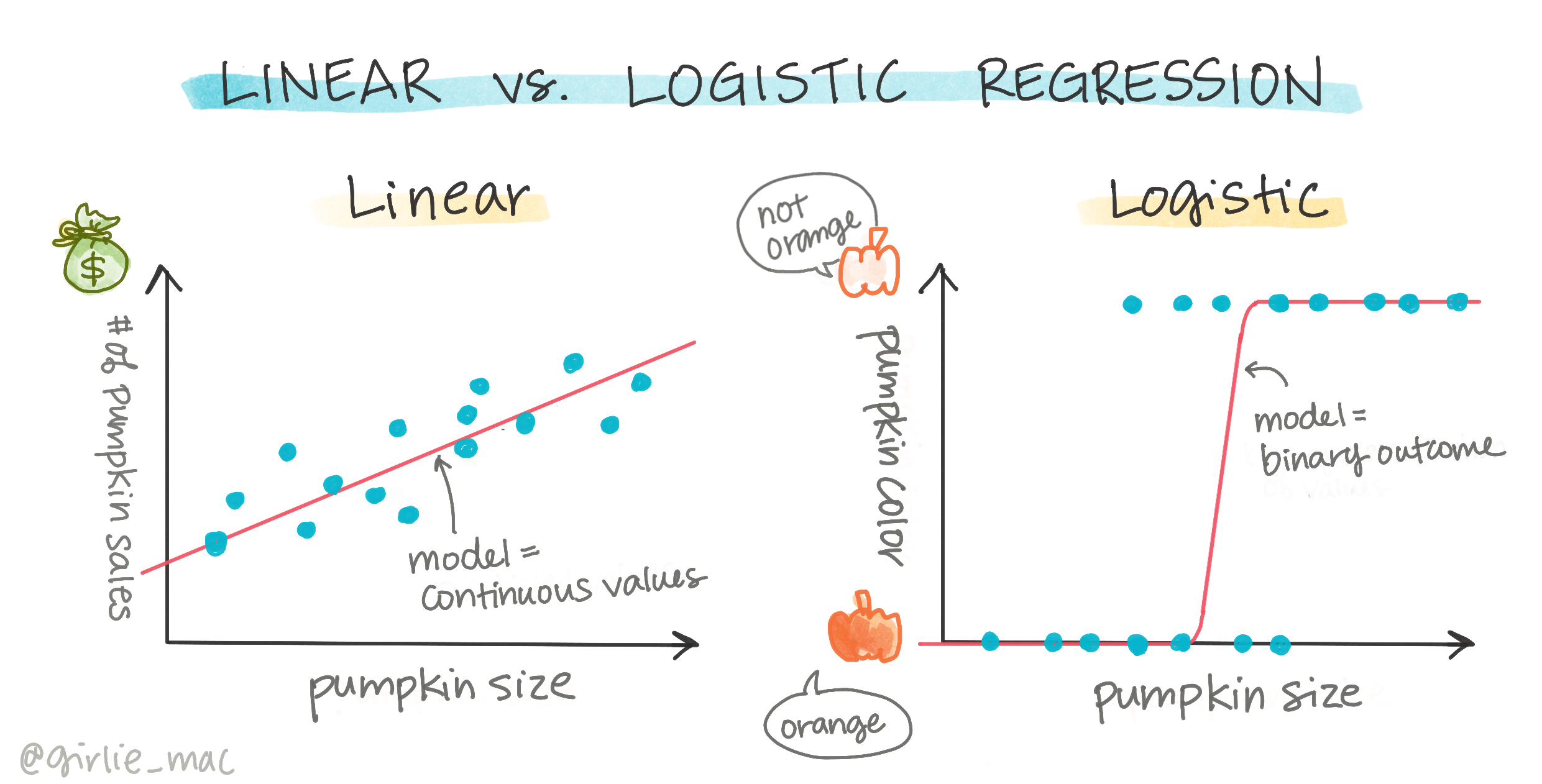
Lojistik regresyon, daha önce öğrendiğiniz doğrusal regresyondan birkaç önemli şekilde farklıdır.

🎥 Lojistik regresyon hakkında kısa bir video özeti için yukarıdaki görsele tıklayın.

İkili Sınıflandırma

Lojistik regresyon, doğrusal regresyonla aynı özellikleri sunmaz. İlki, bir ikili kategori ("beyaz veya beyaz değil") hakkında tahmin sunarken, ikincisi sürekli değerleri tahmin edebilir, örneğin bir balkabağının kökeni ve hasat zamanı verildiğinde, fiyatının ne kadar artacağını.

İnfografik: Dasani Madipalli

Diğer Sınıflandırmalar

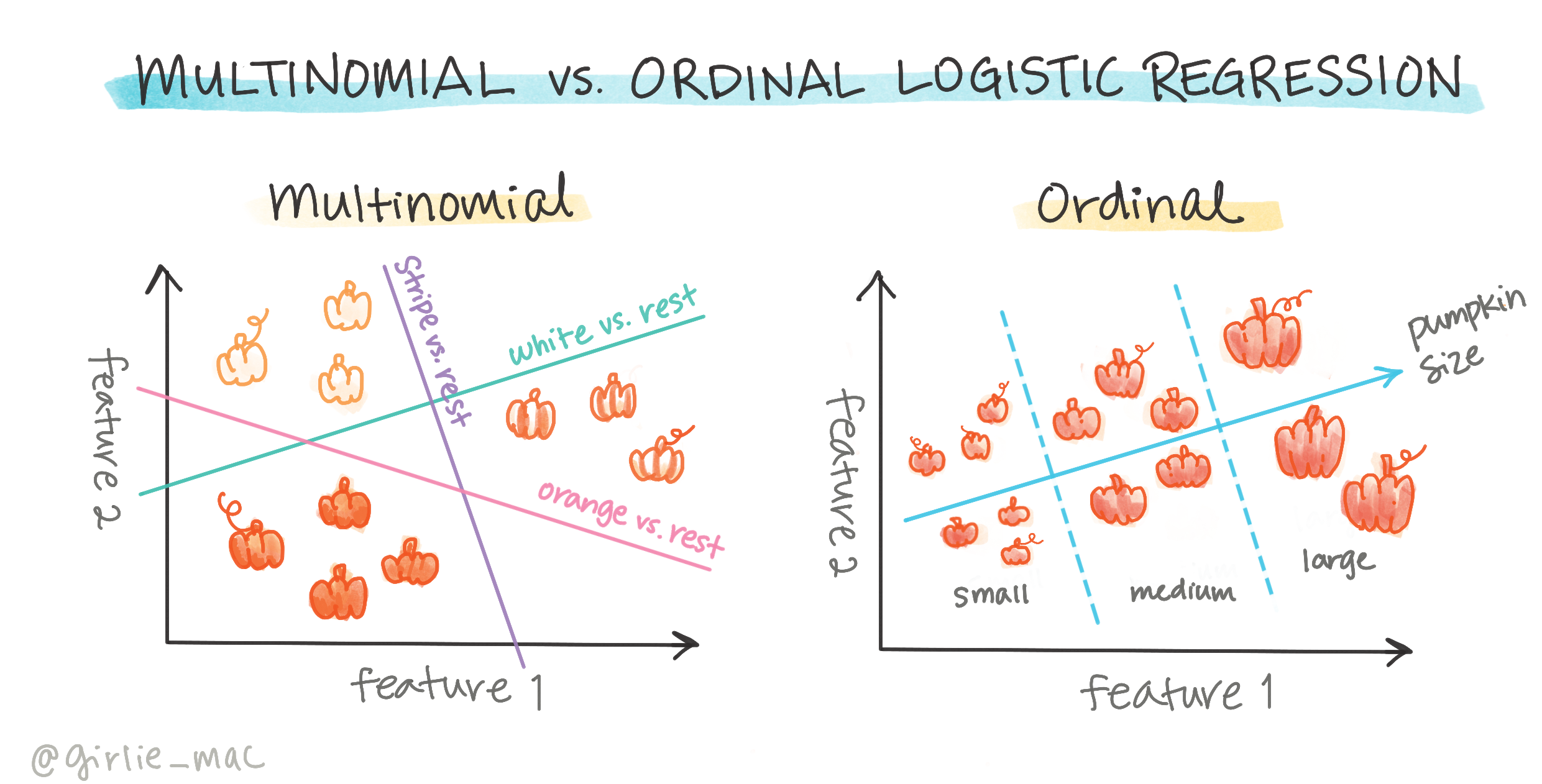
Lojistik regresyonun başka türleri de vardır, bunlar arasında çok terimli ve sıralı olanlar bulunur:

Çok Terimli, birden fazla kategori içerir - "Turuncu, Beyaz ve Çizgili".
Sıralı, mantıksal olarak sıralanmış kategoriler içerir, örneğin sonuçlarımızı mantıksal olarak sıralamak istiyorsak, belirli bir sayıda boyutlara göre sıralanmış balkabakları (mini, küçük, orta, büyük, XL, XXL).

Değişkenlerin Korelasyonlu Olması GEREKMEZ

Doğrusal regresyonun daha fazla korelasyonlu değişkenlerle daha iyi çalıştığını hatırlıyor musunuz? Lojistik regresyon bunun tersidir - değişkenlerin uyumlu olması gerekmez. Bu, zayıf korelasyonlara sahip olan bu veri için işe yarar.

Çok Temiz Veri Gerekir

Lojistik regresyon, daha fazla veri kullanıldığında daha doğru sonuçlar verir; küçük veri setimiz bu görev için optimal değildir, bunu aklınızda bulundurun.

🎥 Doğrusal regresyon için veri hazırlığı hakkında kısa bir video özeti için yukarıdaki görsele tıklayın.

✅ Lojistik regresyona uygun veri türlerini düşünün.

Alıştırma - Veriyi Düzenleme

Öncelikle, eksik değerleri kaldırarak ve yalnızca bazı sütunları seçerek veriyi biraz temizleyin:

Aşağıdaki kodu ekleyin:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Yeni veri çerçevenize her zaman göz atabilirsiniz:

pumpkins.info

Görselleştirme - Kategorik Grafik

Şimdiye kadar balkabağı verilerini içeren başlangıç not defterini yüklediniz ve Renk dahil birkaç değişken içeren bir veri setini koruyacak şekilde temizlediniz. Not defterinde veri çerçevesini farklı bir kütüphane kullanarak görselleştirelim: Seaborn, daha önce kullandığımız Matplotlib üzerine inşa edilmiştir.

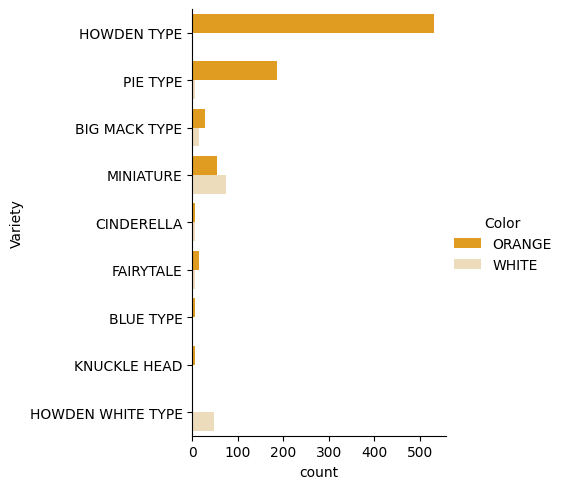
Seaborn, verilerinizi görselleştirmenin bazı güzel yollarını sunar. Örneğin, Çeşit ve Renk için veri dağılımlarını kategorik bir grafikte karşılaştırabilirsiniz.

Balkabağı verilerimiz pumpkins kullanarak ve her balkabağı kategorisi (turuncu veya beyaz) için bir renk eşlemesi belirterek catplot işlevini kullanarak böyle bir grafik oluşturun:
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Verilere bakarak, Renk verisinin Çeşit ile nasıl ilişkili olduğunu görebilirsiniz.

✅ Bu kategorik grafiğe dayanarak, hangi ilginç keşifleri hayal edebilirsiniz?

Veri Ön İşleme: Özellik ve Etiket Kodlama

Balkabağı veri setimiz tüm sütunları için metin değerleri içeriyor. Kategorik verilerle çalışmak insanlar için sezgisel olsa da makineler için değildir. Makine öğrenimi algoritmaları sayılarla daha iyi çalışır. Bu nedenle kodlama, veri ön işleme aşamasında çok önemli bir adımdır, çünkü kategorik verileri sayısal verilere dönüştürmemizi sağlar ve hiçbir bilgi kaybı yaşanmaz. İyi bir kodlama, iyi bir model oluşturmayı sağlar.

Özellik kodlama için iki ana kodlayıcı türü vardır:

Sıralı kodlayıcı: Sıralı değişkenler için uygundur, bunlar kategorik değişkenlerdir ve verileri mantıksal bir sıralamayı takip eder, örneğin veri setimizdeki Ürün Boyutu sütunu. Her kategori bir sayı ile temsil edilir, bu sayı sütundaki kategorinin sırasıdır.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorik kodlayıcı: Mantıksal bir sıralamayı takip etmeyen kategorik değişkenler için uygundur, veri setimizdeki Ürün Boyutu dışındaki tüm özellikler gibi. Bu bir tek-seçim kodlamasıdır, yani her kategori bir ikili sütunla temsil edilir: kodlanmış değişken, balkabağı o Çeşide aitse 1, değilse 0 olur.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Sonrasında, ColumnTransformer kullanılarak birden fazla kodlayıcı tek bir adımda birleştirilir ve uygun sütunlara uygulanır.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Öte yandan, etiketi kodlamak için, scikit-learn LabelEncoder sınıfını kullanırız, bu sınıf etiketleri normalleştirmeye yardımcı olur, böylece yalnızca 0 ile n_classes-1 (burada, 0 ve 1) arasında değerler içerir.

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Özellikleri ve etiketi kodladıktan sonra, bunları yeni bir veri çerçevesi encoded_pumpkins içine birleştirebiliriz.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Ürün Boyutu sütunu için sıralı kodlayıcı kullanmanın avantajları nelerdir?

Değişkenler Arasındaki İlişkileri Analiz Etme

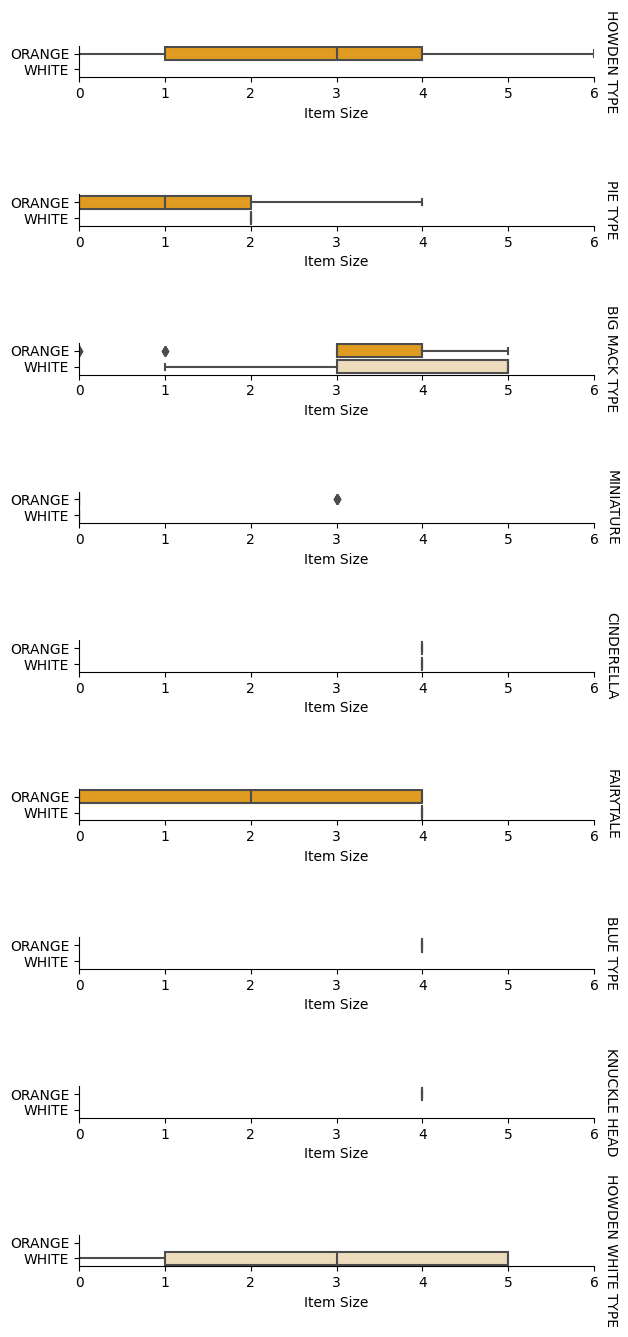
Verilerimizi ön işleme yaptıktan sonra, özellikler ve etiket arasındaki ilişkileri analiz ederek modelin etiketi özelliklere dayanarak ne kadar iyi tahmin edebileceği hakkında bir fikir edinebiliriz. Bu tür bir analizi yapmanın en iyi yolu veriyi görselleştirmektir. Ürün Boyutu, Çeşit ve Renk arasındaki ilişkileri kategorik bir grafikte görselleştirmek için tekrar Seaborn catplot işlevini kullanacağız. Veriyi daha iyi görselleştirmek için kodlanmış Ürün Boyutu sütununu ve kodlanmamış Çeşit sütununu kullanacağız.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Swarm Plot Kullanımı

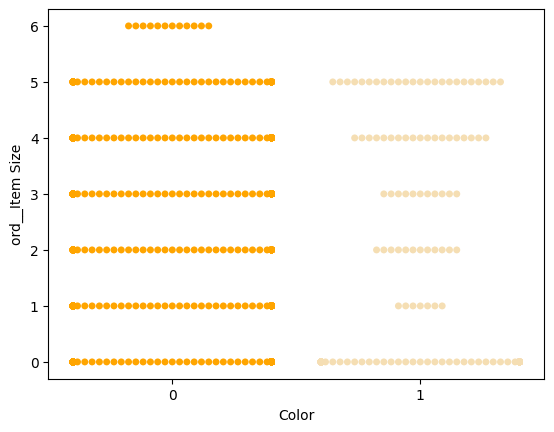
Renk, ikili bir kategori olduğu için (Beyaz veya Beyaz Değil), görselleştirme için 'özel bir yaklaşım' gerektirir. Bu kategorinin diğer değişkenlerle ilişkisini görselleştirmenin başka yolları da vardır.

Seaborn grafikleriyle değişkenleri yan yana görselleştirebilirsiniz.

Değerlerin dağılımını göstermek için bir 'swarm' grafiği deneyin:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Dikkat: Yukarıdaki kod bir uyarı oluşturabilir, çünkü seaborn bu kadar çok veri noktasını bir swarm grafiğinde temsil edemez. Olası bir çözüm, 'size' parametresini kullanarak işaretçi boyutunu küçültmektir. Ancak, bunun grafiğin okunabilirliğini etkilediğini unutmayın.

🧮 Matematiksel Açıklama

Lojistik regresyon, sigmoid fonksiyonları kullanarak 'maksimum olasılık' kavramına dayanır. Bir 'Sigmoid Fonksiyonu' grafikte bir 'S' şekli gibi görünür. Bir değeri alır ve bunu 0 ile 1 arasında bir yere eşler. Eğrisi aynı zamanda 'lojistik eğri' olarak adlandırılır. Formülü şu şekildedir:

Burada sigmoid'in orta noktası x'in 0 noktasında bulunur, L eğrinin maksimum değeridir ve k eğrinin dikliğidir. Fonksiyonun sonucu 0.5'ten büyükse, ilgili etiket ikili seçimin '1' sınıfına atanır. Aksi takdirde, '0' olarak sınıflandırılır.

Modelinizi Oluşturun

Bu ikili sınıflandırmayı bulmak için bir model oluşturmak Scikit-learn'de şaşırtıcı derecede basittir.

🎥 Doğrusal regresyon modeli oluşturma hakkında kısa bir video özeti için yukarıdaki görsele tıklayın.

Sınıflandırma modelinizde kullanmak istediğiniz değişkenleri seçin ve train_test_split() çağırarak eğitim ve test setlerini ayırın:

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Şimdi modelinizi, eğitim verilerinizle fit() çağırarak eğitebilir ve sonucunu yazdırabilirsiniz:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Modelinizin skor tablosuna bir göz atın. Yaklaşık 1000 satır veriyle çalıştığınızı düşünürsek fena değil:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Daha İyi Anlama İçin Bir Karışıklık Matrisi

Yukarıdaki öğeleri yazdırarak terimler ile bir skor tablosu raporu alabilirsiniz, ancak modelinizi daha kolay anlayabilmek için bir karışıklık matrisi kullanabilirsiniz.

🎓 'Karışıklık matrisi' (veya 'hata matrisi'), modelinizin doğru ve yanlış pozitif ve negatiflerini ifade eden bir tablodur, böylece tahminlerin doğruluğunu ölçer.

Bir karışıklık matrisi kullanmak için confusion_matrix() çağırın:

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Modelinizin karışıklık matrisine bir göz atın:

array([[162,   4],
       [ 11,  22]])

Scikit-learn'de karışıklık matrisleri Satırlar (ekseni 0) gerçek etiketlerdir ve sütunlar (ekseni 1) tahmin edilen etiketlerdir.

	0	1
0	TN	FP
1	FN	TP

Burada neler oluyor? Diyelim ki modelimiz balkabaklarını iki ikili kategori arasında sınıflandırmakla görevlendirildi: kategori 'beyaz' ve kategori 'beyaz değil'.

Modeliniz bir balkabağını beyaz değil olarak tahmin ederse ve gerçekten 'beyaz değil' kategorisine aitse buna doğru negatif denir, sol üstteki sayı ile gösterilir.
Modeliniz bir balkabağını beyaz olarak tahmin ederse ve gerçekten 'beyaz değil' kategorisine aitse buna yanlış negatif denir, sol alttaki sayı ile gösterilir.
Modeliniz bir balkabağını beyaz değil olarak tahmin ederse ve gerçekten 'beyaz' kategorisine aitse buna yanlış pozitif denir, sağ üstteki sayı ile gösterilir.
Modeliniz bir balkabağını beyaz olarak tahmin ederse ve gerçekten 'beyaz' kategorisine aitse buna doğru pozitif denir, sağ alttaki sayı ile gösterilir.

Tahmin edebileceğiniz gibi, daha fazla doğru pozitif ve doğru negatif ve daha az yanlış pozitif ve yanlış negatif olması tercih edilir, bu da modelin daha iyi performans gösterdiğini ifade eder. Confusion matrisinin kesinlik ve geri çağırma ile ilişkisi nedir? Yukarıda yazdırılan sınıflandırma raporu kesinlik (0.85) ve geri çağırma (0.67) değerlerini göstermişti.

Kesinlik = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Geri çağırma = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ S: Confusion matrisine göre model nasıl performans gösterdi? C: Fena değil; iyi bir miktarda doğru negatif var ancak birkaç yanlış negatif de mevcut.

Confusion matrisinin TP/TN ve FP/FN haritalaması yardımıyla daha önce gördüğümüz terimleri tekrar gözden geçirelim:

🎓 Kesinlik: TP/(TP + FP) Alınan örnekler arasında doğru olanların oranı (örneğin, hangi etiketler doğru şekilde etiketlendi)

🎓 Geri çağırma: TP/(TP + FN) Alınan örnekler arasında doğru olanların oranı, doğru etiketlenmiş olsun ya da olmasın

🎓 f1-skoru: (2 * kesinlik * geri çağırma)/(kesinlik + geri çağırma) Kesinlik ve geri çağırmanın ağırlıklı ortalaması, en iyi değer 1, en kötü değer 0

🎓 Destek: Alınan her bir etiketin kaç kez ortaya çıktığı

🎓 Doğruluk: (TP + TN)/(TP + TN + FP + FN) Bir örnek için doğru şekilde tahmin edilen etiketlerin yüzdesi.

🎓 Makro Ortalama: Her bir etiket için ağırlıksız ortalama metriklerin hesaplanması, etiket dengesizliği dikkate alınmaz.

🎓 Ağırlıklı Ortalama: Her bir etiket için metriklerin ortalamasının hesaplanması, etiket dengesizliğini destekle (her bir etiket için doğru örnek sayısı) ile ağırlıklandırarak dikkate alır.

✅ Modelinizin yanlış negatif sayısını azaltmasını istiyorsanız hangi metriği takip etmeniz gerektiğini düşünebilir misiniz?

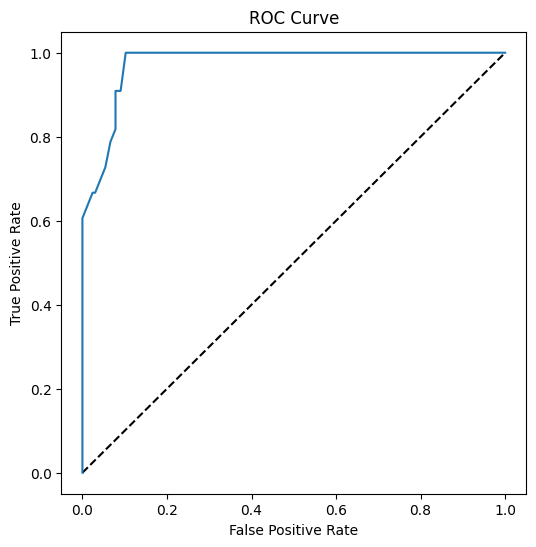
Bu modelin ROC eğrisini görselleştirin

🎥 Yukarıdaki görsele tıklayarak ROC eğrileri hakkında kısa bir video izleyebilirsiniz.

Hadi 'ROC' eğrisini görmek için bir görselleştirme daha yapalım:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Matplotlib kullanarak modelin Alıcı İşletim Karakteristiği veya ROC'sini çizin. ROC eğrileri genellikle bir sınıflandırıcının çıktısını doğru ve yanlış pozitifler açısından görmek için kullanılır. "ROC eğrileri genellikle Y ekseninde doğru pozitif oranı ve X ekseninde yanlış pozitif oranı gösterir." Bu nedenle eğrinin dikliği ve orta çizgi ile eğri arasındaki boşluk önemlidir: eğrinin hızla yukarı ve çizginin üzerine çıkmasını istersiniz. Bizim durumumuzda, başlangıçta yanlış pozitifler var ve ardından çizgi düzgün bir şekilde yukarı ve üzerine çıkıyor:

Son olarak, Scikit-learn'ün roc_auc_score API'sini kullanarak gerçek 'Eğri Altındaki Alan'ı (AUC) hesaplayın:

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Sonuç 0.9749908725812341. AUC'nin 0 ile 1 arasında değiştiği göz önüne alındığında, büyük bir skor istiyorsunuz çünkü tahminlerinde %100 doğru olan bir modelin AUC'si 1 olacaktır; bu durumda model oldukça iyi.

Gelecekteki sınıflandırma derslerinde, modelinizin skorlarını iyileştirmek için nasıl yineleme yapacağınızı öğreneceksiniz. Ama şimdilik, tebrikler! Bu regresyon derslerini tamamladınız!

🚀Meydan Okuma

Lojistik regresyon hakkında keşfedilecek çok şey var! Ancak öğrenmenin en iyi yolu denemektir. Bu tür bir analize uygun bir veri seti bulun ve onunla bir model oluşturun. Ne öğreniyorsunuz? ipucu: Kaggle üzerinde ilginç veri setleri arayın.

Ders sonrası test

Gözden Geçirme ve Kendi Kendine Çalışma

Stanford'dan bu makalenin ilk birkaç sayfasını okuyun ve lojistik regresyonun bazı pratik kullanımlarını inceleyin. Şimdiye kadar incelediğimiz regresyon türlerinden hangisinin hangi görevler için daha uygun olduğunu düşünün. Hangisi en iyi çalışır?

Ödev

Bu regresyonu tekrar deneyin

Feragatname:
Bu belge, AI çeviri hizmeti Co-op Translator kullanılarak çevrilmiştir. Doğruluk için çaba göstersek de, otomatik çevirilerin hata veya yanlışlık içerebileceğini lütfen unutmayın. Belgenin orijinal dili, yetkili kaynak olarak kabul edilmelidir. Kritik bilgiler için profesyonel insan çevirisi önerilir. Bu çevirinin kullanımından kaynaklanan yanlış anlamalar veya yanlış yorumlamalar için sorumluluk kabul etmiyoruz.

23 KiB Raw Permalink Blame History Unescape Escape