12 KiB

Raw Permalink Blame History

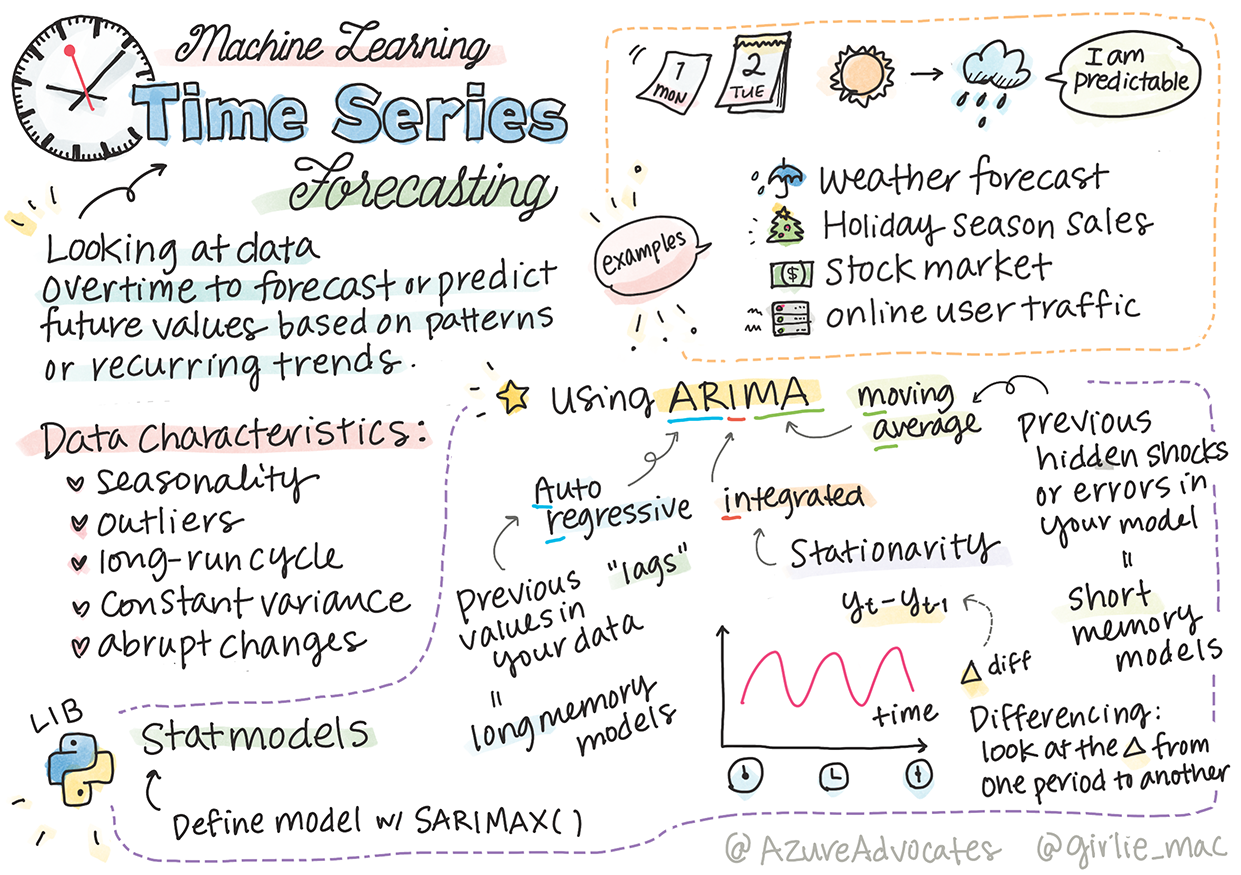
Introduktion till tidsserieprognostisering

Sketchnote av Tomomi Imura

I den här lektionen och nästa kommer du att lära dig lite om tidsserieprognostisering, en intressant och värdefull del av en ML-forskares verktygslåda som är något mindre känd än andra ämnen. Tidsserieprognostisering är som en sorts "kristallkula": baserat på tidigare prestationer av en variabel, som pris, kan du förutsäga dess framtida potentiella värde.

🎥 Klicka på bilden ovan för en video om tidsserieprognostisering

Quiz före föreläsningen

Det är ett användbart och intressant område med verkligt värde för företag, tack vare dess direkta tillämpning på problem som prissättning, lagerhantering och leveranskedjeproblem. Även om djupinlärningstekniker har börjat användas för att få bättre insikter och förbättra prognoser, är tidsserieprognostisering fortfarande ett område som i hög grad bygger på klassiska ML-tekniker.

Penn States användbara läroplan för tidsserier finns här

Introduktion

Anta att du underhåller en uppsättning smarta parkeringsmätare som ger data om hur ofta de används och hur länge över tid.

Tänk om du kunde förutsäga, baserat på mätarens tidigare prestationer, dess framtida värde enligt utbud och efterfrågan?

Att noggrant förutsäga när man ska agera för att uppnå sitt mål är en utmaning som kan hanteras med tidsserieprognostisering. Det skulle kanske inte göra folk glada att behöva betala mer under hektiska tider när de letar efter en parkeringsplats, men det skulle definitivt vara ett sätt att generera intäkter för att hålla gatorna rena!

Låt oss utforska några typer av algoritmer för tidsserier och börja med en notebook för att rensa och förbereda data. De data du kommer att analysera är hämtade från GEFCom2014-prognostävlingen. Den består av tre års timvisa elförbruknings- och temperaturvärden mellan 2012 och 2014. Givet de historiska mönstren för elförbrukning och temperatur kan du förutsäga framtida värden för elförbrukning.

I det här exemplet kommer du att lära dig att förutsäga ett steg framåt i tiden, med hjälp av endast historiska förbrukningsdata. Innan vi börjar är det dock bra att förstå vad som händer bakom kulisserna.

Några definitioner

När du stöter på termen "tidsserie" behöver du förstå dess användning i flera olika sammanhang.

🎓 Tidsserie

Inom matematik är "en tidsserie en serie datapunkter indexerade (eller listade eller plottade) i tidsordning. Vanligtvis är en tidsserie en sekvens som tas vid successiva lika avstånd i tid." Ett exempel på en tidsserie är det dagliga slutvärdet för Dow Jones Industrial Average. Användningen av tidsserieplottar och statistisk modellering är vanligt förekommande inom signalbehandling, väderprognoser, jordbävningsförutsägelser och andra områden där händelser inträffar och datapunkter kan plottas över tid.

🎓 Tidsserieanalys

Tidsserieanalys är analysen av ovan nämnda tidsseriedata. Tidsseriedata kan ta olika former, inklusive "avbrutna tidsserier" som upptäcker mönster i en tidsseries utveckling före och efter en avbrytande händelse. Typen av analys som behövs för tidsserien beror på datans natur. Tidsseriedata kan i sig ta formen av serier av siffror eller tecken.

Analysen som ska utföras använder en mängd olika metoder, inklusive frekvensdomän och tidsdomän, linjära och icke-linjära metoder och mer. Läs mer om de många sätten att analysera denna typ av data.

🎓 Tidsserieprognostisering

Tidsserieprognostisering är användningen av en modell för att förutsäga framtida värden baserat på mönster som visas av tidigare insamlade data. Även om det är möjligt att använda regressionsmodeller för att utforska tidsseriedata, med tidsindex som x-variabler i ett diagram, analyseras sådan data bäst med hjälp av speciella typer av modeller.

Tidsseriedata är en lista över ordnade observationer, till skillnad från data som kan analyseras med linjär regression. Den vanligaste modellen är ARIMA, en akronym för "Autoregressive Integrated Moving Average".

ARIMA-modeller "relaterar det nuvarande värdet av en serie till tidigare värden och tidigare prognosfel." De är mest lämpliga för att analysera tidsdomänsdata, där data är ordnade över tid.

Det finns flera typer av ARIMA-modeller, som du kan lära dig om här och som du kommer att beröra i nästa lektion.

I nästa lektion kommer du att bygga en ARIMA-modell med hjälp av Univariate Time Series, som fokuserar på en variabel som ändrar sitt värde över tid. Ett exempel på denna typ av data är denna dataset som registrerar den månatliga CO2-koncentrationen vid Mauna Loa-observatoriet:

CO2	YearMonth	Year	Month
330.62	1975.04	1975	1
331.40	1975.13	1975	2
331.87	1975.21	1975	3
333.18	1975.29	1975	4
333.92	1975.38	1975	5
333.43	1975.46	1975	6
331.85	1975.54	1975	7
330.01	1975.63	1975	8
328.51	1975.71	1975	9
328.41	1975.79	1975	10
329.25	1975.88	1975	11
330.97	1975.96	1975	12

✅ Identifiera variabeln som ändras över tid i denna dataset

Egenskaper hos tidsseriedata att beakta

När du tittar på tidsseriedata kan du märka att den har vissa egenskaper som du behöver ta hänsyn till och hantera för att bättre förstå dess mönster. Om du betraktar tidsseriedata som potentiellt tillhandahållande av en "signal" som du vill analysera, kan dessa egenskaper betraktas som "brus". Du kommer ofta att behöva minska detta "brus" genom att hantera vissa av dessa egenskaper med statistiska tekniker.

Här är några begrepp du bör känna till för att kunna arbeta med tidsserier:

🎓 Trender

Trender definieras som mätbara ökningar och minskningar över tid. Läs mer. I samband med tidsserier handlar det om hur man använder och, om nödvändigt, tar bort trender från din tidsserie.

🎓 Säsongsvariationer

Säsongsvariationer definieras som periodiska fluktuationer, som exempelvis försäljningsökningar under helger. Ta en titt på hur olika typer av diagram visar säsongsvariationer i data.

🎓 Avvikare

Avvikare är datapunkter som ligger långt ifrån den normala datavariationen.

🎓 Långsiktiga cykler

Oberoende av säsongsvariationer kan data visa en långsiktig cykel, som en ekonomisk nedgång som varar längre än ett år.

🎓 Konstant varians

Över tid kan vissa data visa konstanta fluktuationer, som energianvändning dag och natt.

🎓 Plötsliga förändringar

Data kan visa en plötslig förändring som kan behöva ytterligare analys. Den plötsliga stängningen av företag på grund av COVID, till exempel, orsakade förändringar i data.

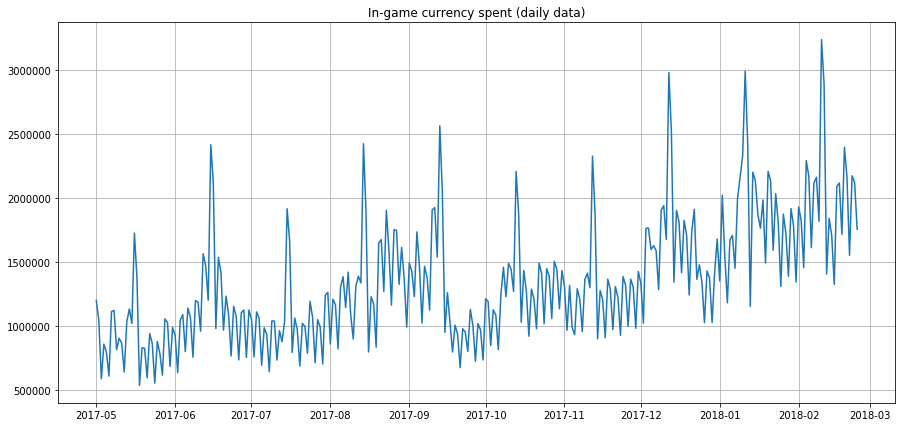
✅ Här är ett exempel på ett tidsseriediagram som visar dagliga utgifter för spelvaluta över några år. Kan du identifiera några av de egenskaper som listas ovan i denna data?

Övning - Kom igång med data om elförbrukning

Låt oss börja skapa en tidsseriemodell för att förutsäga framtida elförbrukning baserat på tidigare förbrukning.

Datan i detta exempel är hämtad från GEFCom2014-prognostävlingen. Den består av tre års timvisa elförbruknings- och temperaturvärden mellan 2012 och 2014.

Tao Hong, Pierre Pinson, Shu Fan, Hamidreza Zareipour, Alberto Troccoli och Rob J. Hyndman, "Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond", International Journal of Forecasting, vol.32, no.3, pp 896-913, juli-september, 2016.

I mappen working för denna lektion, öppna filen notebook.ipynb. Börja med att lägga till bibliotek som hjälper dig att ladda och visualisera data:
```
import os
import matplotlib.pyplot as plt
from common.utils import load_data
%matplotlib inline
```
Observera att du använder filerna från den inkluderade mappen common som ställer in din miljö och hanterar nedladdning av data.
Undersök sedan datan som en dataframe genom att anropa load_data() och head():
```
data_dir = './data'
energy = load_data(data_dir)[['load']]
energy.head()
```
Du kan se att det finns två kolumner som representerar datum och förbrukning:

load

2012-01-01 00:00:00 2698.0

2012-01-01 01:00:00 2558.0

2012-01-01 02:00:00 2444.0

2012-01-01 03:00:00 2402.0

2012-01-01 04:00:00 2403.0

	load
2012-01-01 00:00:00	2698.0
2012-01-01 01:00:00	2558.0
2012-01-01 02:00:00	2444.0
2012-01-01 03:00:00	2402.0
2012-01-01 04:00:00	2403.0

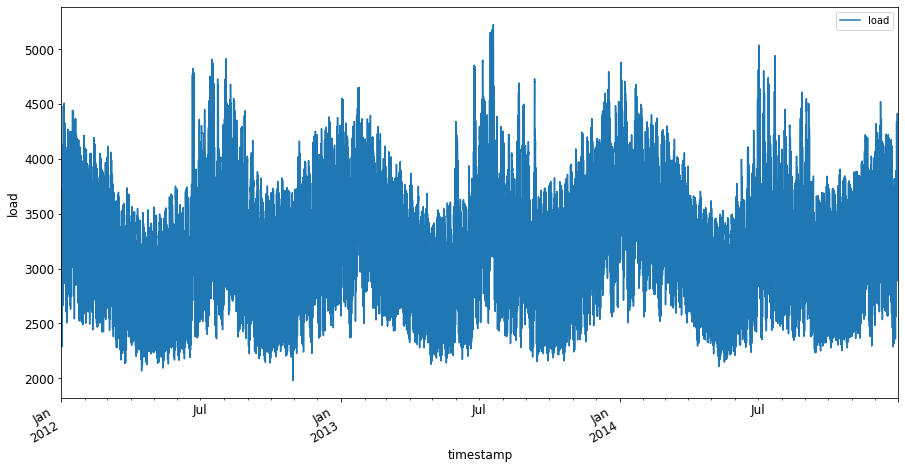
Nu, plotta datan genom att anropa plot():

energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

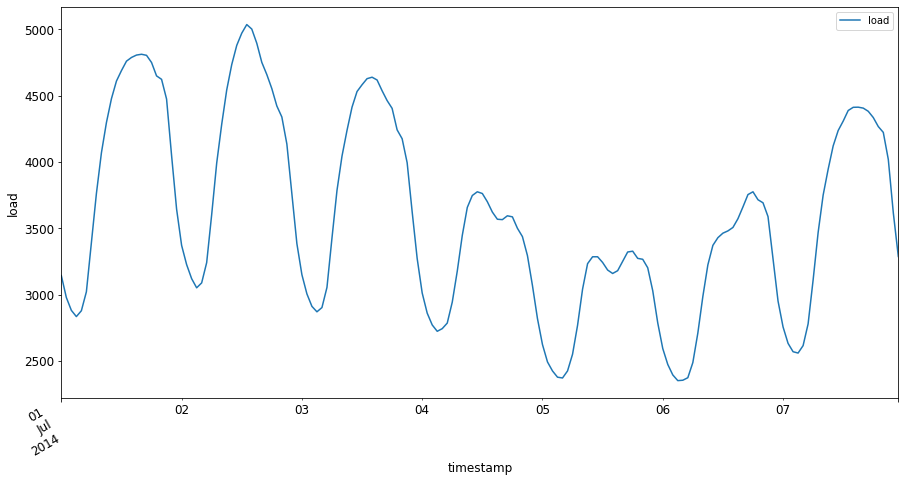
Plotta nu den första veckan i juli 2014 genom att ange den som input till energy i mönstret [från datum]: [till datum]:
```
energy['2014-07-01':'2014-07-07'].plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Ett vackert diagram! Titta på dessa diagram och se om du kan identifiera några av de egenskaper som listas ovan. Vad kan vi dra för slutsatser genom att visualisera datan?

I nästa lektion kommer du att skapa en ARIMA-modell för att göra några prognoser.

🚀Utmaning

Gör en lista över alla branscher och forskningsområden du kan tänka dig som skulle dra nytta av tidsserieprognostisering. Kan du tänka dig en tillämpning av dessa tekniker inom konst? Inom ekonometrik? Ekologi? Detaljhandel? Industri? Finans? Var annars?

Quiz efter föreläsningen

Granskning & Självstudier

Även om vi inte kommer att täcka dem här, används ibland neurala nätverk för att förbättra klassiska metoder för tidsserieprognostisering. Läs mer om dem i denna artikel

Uppgift

Visualisera fler tidsserier

Ansvarsfriskrivning:
Detta dokument har översatts med hjälp av AI-översättningstjänsten Co-op Translator. Även om vi strävar efter noggrannhet, vänligen notera att automatiska översättningar kan innehålla fel eller felaktigheter. Det ursprungliga dokumentet på dess originalspråk bör betraktas som den auktoritativa källan. För kritisk information rekommenderas professionell mänsklig översättning. Vi ansvarar inte för eventuella missförstånd eller feltolkningar som uppstår vid användning av denna översättning.

12 KiB Raw Permalink Blame History