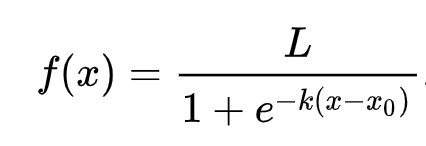22 KiB

Raw Permalink Blame History

Logistisk regression för att förutsäga kategorier

Quiz före föreläsning

Denna lektion finns tillgänglig i R!

Introduktion

I denna sista lektion om regression, en av de grundläggande klassiska ML-teknikerna, ska vi titta på logistisk regression. Du kan använda denna teknik för att upptäcka mönster och förutsäga binära kategorier. Är detta godis choklad eller inte? Är denna sjukdom smittsam eller inte? Kommer denna kund att välja denna produkt eller inte?

I denna lektion kommer du att lära dig:

Ett nytt bibliotek för datavisualisering
Tekniker för logistisk regression

✅ Fördjupa din förståelse för att arbeta med denna typ av regression i detta Learn-modul

Förkunskaper

Efter att ha arbetat med pumpadatan är vi nu tillräckligt bekanta med den för att inse att det finns en binär kategori vi kan arbeta med: Color.

Låt oss bygga en modell för logistisk regression för att förutsäga vilken färg en given pumpa sannolikt har (orange 🎃 eller vit 👻), baserat på vissa variabler.

Varför pratar vi om binär klassificering i en lektion om regression? Endast av språklig bekvämlighet, eftersom logistisk regression egentligen är en klassificeringsmetod, även om den är linjärbaserad. Lär dig om andra sätt att klassificera data i nästa lektionsgrupp.

Definiera frågan

För våra ändamål kommer vi att uttrycka detta som en binär: 'Vit' eller 'Inte vit'. Det finns också en 'randig' kategori i vår dataset, men det finns få instanser av den, så vi kommer inte att använda den. Den försvinner ändå när vi tar bort nullvärden från datasetet.

🎃 Rolig fakta: vi kallar ibland vita pumpor för 'spökpumpor'. De är inte särskilt lätta att skära, så de är inte lika populära som de orangea, men de ser coola ut! Så vi kan också formulera om vår fråga som: 'Spöke' eller 'Inte spöke'. 👻

Om logistisk regression

Logistisk regression skiljer sig från linjär regression, som du lärde dig om tidigare, på några viktiga sätt.

🎥 Klicka på bilden ovan för en kort videoöversikt av logistisk regression.

Binär klassificering

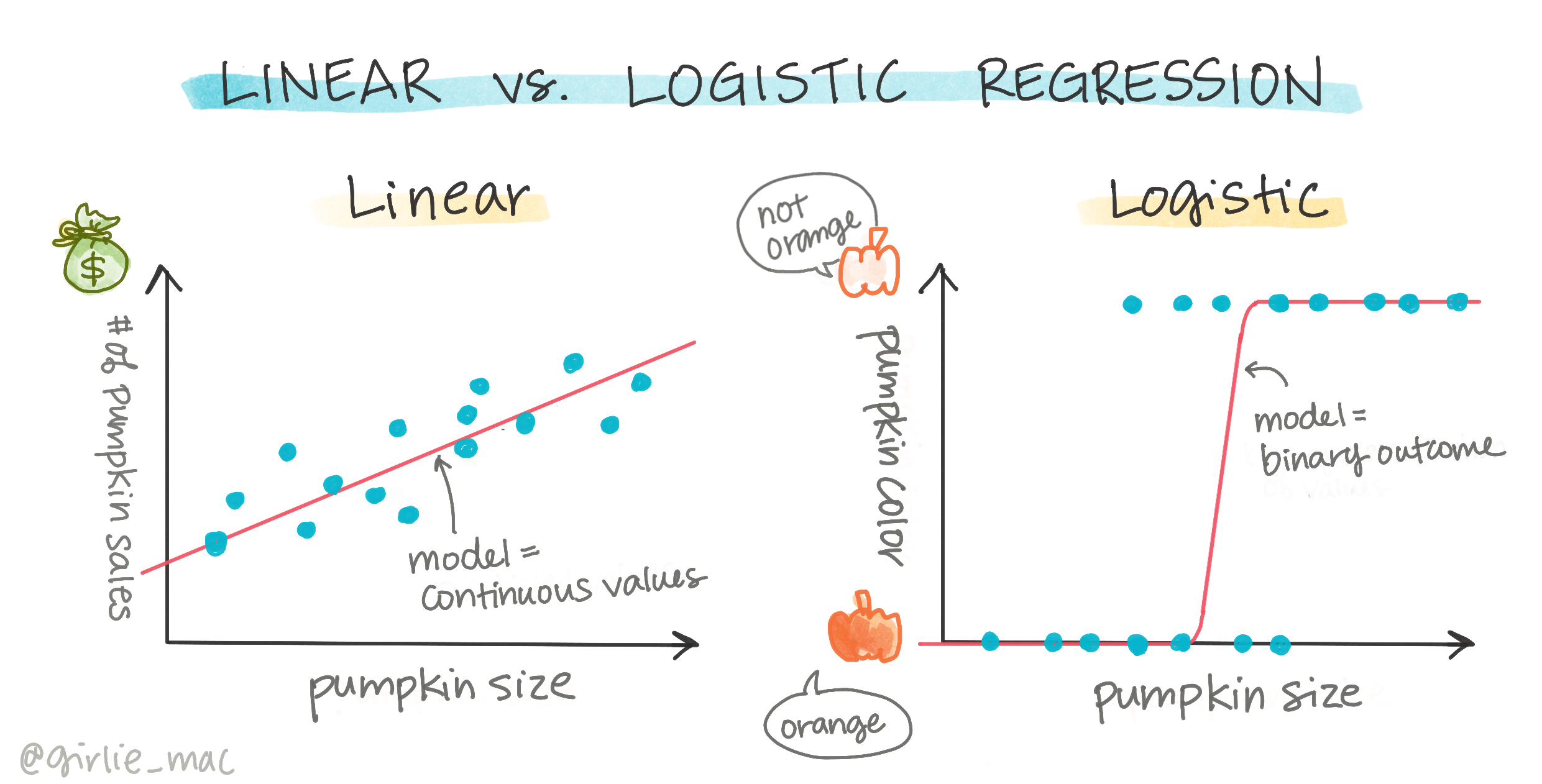
Logistisk regression erbjuder inte samma funktioner som linjär regression. Den förstnämnda ger en förutsägelse om en binär kategori ("vit eller inte vit"), medan den senare kan förutsäga kontinuerliga värden, till exempel givet ursprunget av en pumpa och skördetiden, hur mycket dess pris kommer att stiga.

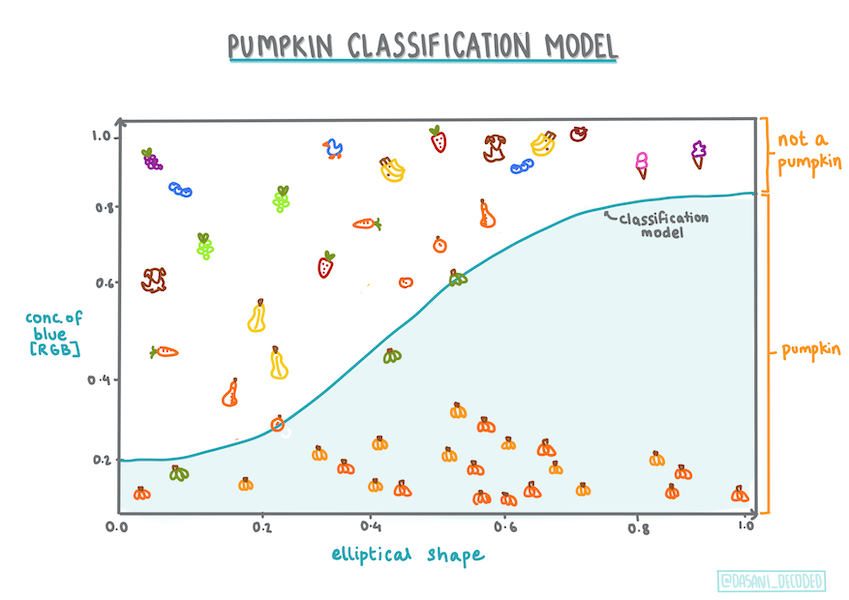
Infografik av Dasani Madipalli

Andra klassificeringar

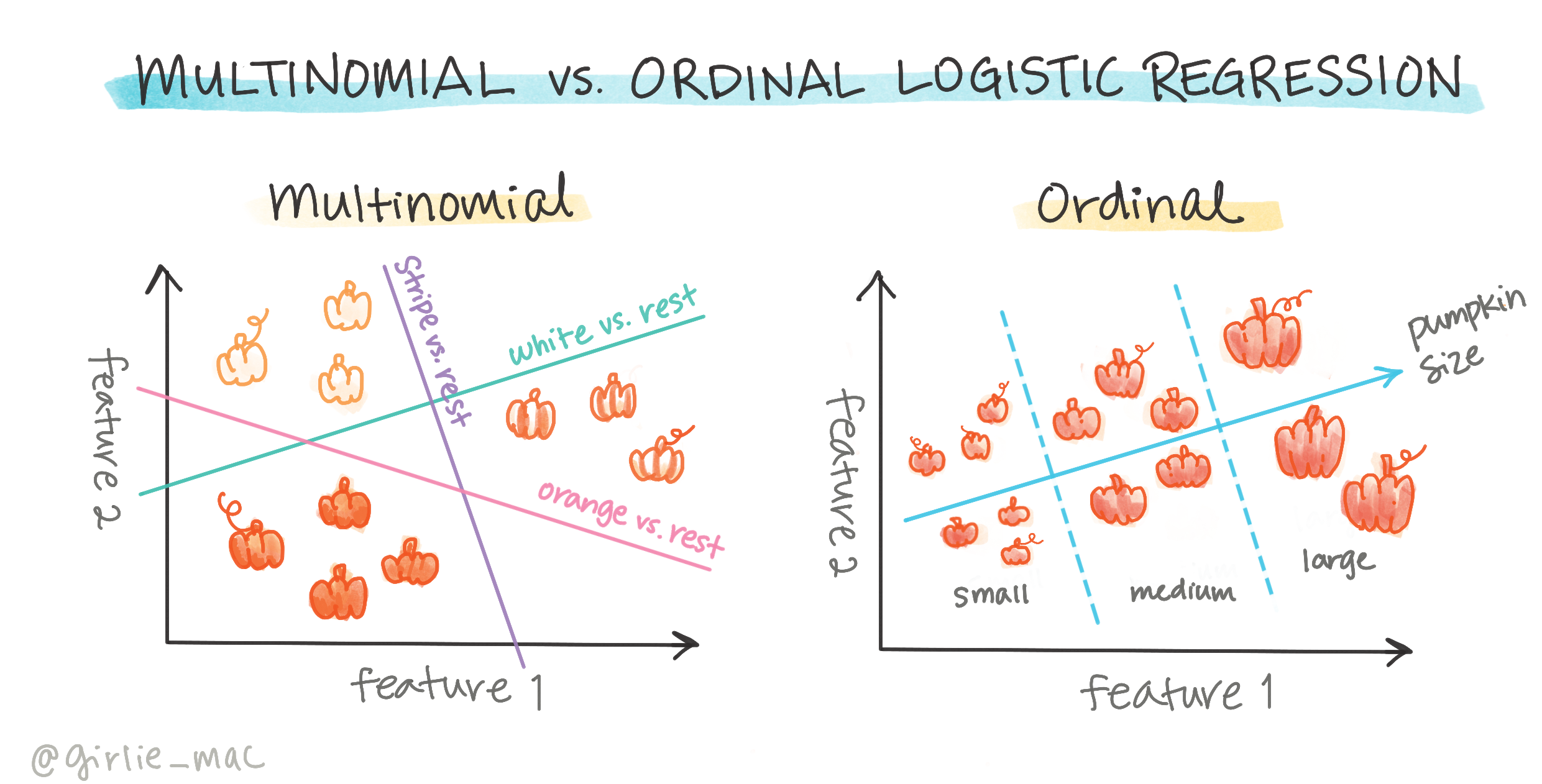
Det finns andra typer av logistisk regression, inklusive multinomial och ordinal:

Multinomial, som innebär att ha mer än en kategori - "Orange, Vit och Randig".
Ordinal, som innebär ordnade kategorier, användbart om vi vill ordna våra resultat logiskt, som våra pumpor som är ordnade efter ett begränsat antal storlekar (mini, sm, med, lg, xl, xxl).

Variabler BEHÖVER INTE korrelera

Kommer du ihåg hur linjär regression fungerade bättre med mer korrelerade variabler? Logistisk regression är motsatsen - variablerna behöver inte stämma överens. Det fungerar för denna data som har något svaga korrelationer.

Du behöver mycket ren data

Logistisk regression ger mer exakta resultat om du använder mer data; vårt lilla dataset är inte optimalt för denna uppgift, så ha det i åtanke.

🎥 Klicka på bilden ovan för en kort videoöversikt av att förbereda data för linjär regression

✅ Fundera på vilka typer av data som skulle passa bra för logistisk regression

Övning - städa datan

Först, städa datan lite, ta bort nullvärden och välj endast några av kolumnerna:

Lägg till följande kod:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Du kan alltid ta en titt på din nya dataframe:

pumpkins.info

Visualisering - kategoriskt diagram

Vid det här laget har du laddat upp startnotebooken med pumpadatan igen och städat den för att bevara ett dataset som innehåller några variabler, inklusive Color. Låt oss visualisera dataframe i notebooken med ett annat bibliotek: Seaborn, som är byggt på Matplotlib som vi använde tidigare.

Seaborn erbjuder några smarta sätt att visualisera din data. Till exempel kan du jämföra distributioner av datan för varje Variety och Color i ett kategoriskt diagram.

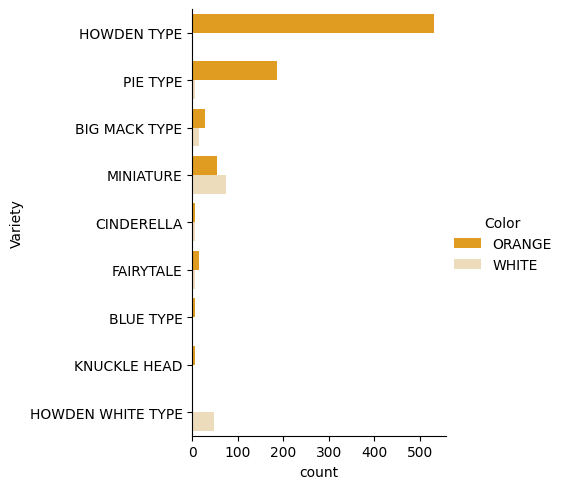
Skapa ett sådant diagram genom att använda funktionen catplot, med vår pumpadata pumpkins, och specificera en färgkartläggning för varje pumpakategori (orange eller vit):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Genom att observera datan kan du se hur färgdata relaterar till sort.

✅ Givet detta kategoriska diagram, vilka intressanta undersökningar kan du föreställa dig?

Datapreparation: kodning av funktioner och etiketter

Vårt pumpadataset innehåller strängvärden för alla dess kolumner. Att arbeta med kategorisk data är intuitivt för människor men inte för maskiner. Maskininlärningsalgoritmer fungerar bra med siffror. Därför är kodning ett mycket viktigt steg i datapreparationsfasen, eftersom det gör det möjligt för oss att omvandla kategorisk data till numerisk data utan att förlora någon information. Bra kodning leder till att bygga en bra modell.

För kodning av funktioner finns det två huvudtyper av kodare:

Ordinal kodare: passar bra för ordnade variabler, som är kategoriska variabler där deras data följer en logisk ordning, som kolumnen Item Size i vårt dataset. Den skapar en kartläggning så att varje kategori representeras av ett nummer, vilket är ordningen på kategorin i kolumnen.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorisk kodare: passar bra för nominella variabler, som är kategoriska variabler där deras data inte följer en logisk ordning, som alla funktioner utom Item Size i vårt dataset. Det är en one-hot-kodning, vilket innebär att varje kategori representeras av en binär kolumn: den kodade variabeln är lika med 1 om pumpan tillhör den sorten och 0 annars.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Sedan används ColumnTransformer för att kombinera flera kodare i ett enda steg och tillämpa dem på de lämpliga kolumnerna.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Å andra sidan, för att koda etiketten, använder vi scikit-learn-klassen LabelEncoder, som är en hjälpsklass för att normalisera etiketter så att de endast innehåller värden mellan 0 och n_classes-1 (här, 0 och 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

När vi har kodat funktionerna och etiketten kan vi slå samman dem till en ny dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Vilka är fördelarna med att använda en ordinal kodare för kolumnen Item Size?

Analysera relationer mellan variabler

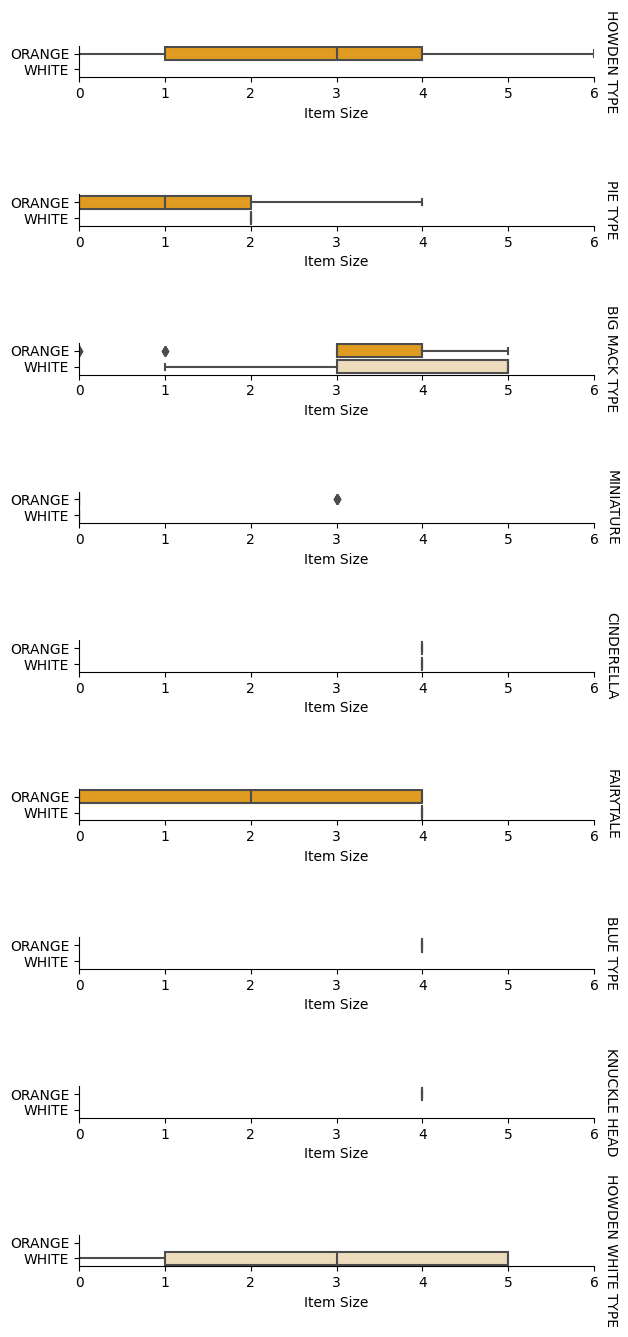
Nu när vi har förberett vår data kan vi analysera relationerna mellan funktionerna och etiketten för att få en uppfattning om hur väl modellen kommer att kunna förutsäga etiketten baserat på funktionerna. Det bästa sättet att utföra denna typ av analys är att plotta datan. Vi kommer att använda Seaborns funktion catplot igen för att visualisera relationerna mellan Item Size, Variety och Color i ett kategoriskt diagram. För att bättre plotta datan kommer vi att använda den kodade kolumnen Item Size och den okodade kolumnen Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Använd ett swarm-diagram

Eftersom Color är en binär kategori (Vit eller Inte), behöver den 'en specialiserad metod för visualisering'. Det finns andra sätt att visualisera relationen mellan denna kategori och andra variabler.

Du kan visualisera variabler sida vid sida med Seaborn-diagram.

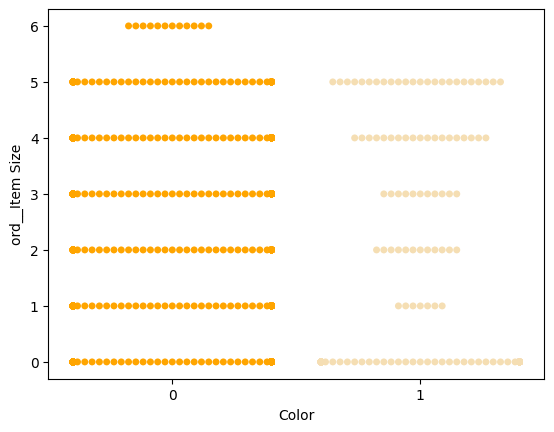
Prova ett 'swarm'-diagram för att visa distributionen av värden:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Observera: koden ovan kan generera en varning, eftersom Seaborn misslyckas med att representera en sådan mängd datapunkter i ett swarm-diagram. En möjlig lösning är att minska storleken på markören genom att använda parametern 'size'. Men var medveten om att detta påverkar läsbarheten av diagrammet.

🧮 Visa mig matematiken

Logistisk regression bygger på konceptet 'maximum likelihood' med hjälp av sigmoidfunktioner. En 'Sigmoidfunktion' på ett diagram ser ut som en 'S'-form. Den tar ett värde och kartlägger det till någonstans mellan 0 och 1. Dess kurva kallas också för en 'logistisk kurva'. Dess formel ser ut så här:

där sigmoids mittpunkt befinner sig vid x:s 0-punkt, L är kurvans maximala värde, och k är kurvans branthet. Om resultatet av funktionen är mer än 0.5, kommer etiketten i fråga att ges klassen '1' av det binära valet. Om inte, kommer den att klassificeras som '0'.

Bygg din modell

Att bygga en modell för att hitta dessa binära klassificeringar är förvånansvärt enkelt i Scikit-learn.

🎥 Klicka på bilden ovan för en kort videoöversikt av att bygga en linjär regressionsmodell

Välj de variabler du vill använda i din klassificeringsmodell och dela upp tränings- och testuppsättningarna genom att kalla på train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Nu kan du träna din modell genom att kalla på fit() med din träningsdata och skriva ut dess resultat:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Ta en titt på din modells poängrapport. Den är inte dålig, med tanke på att du bara har cirka 1000 rader data:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Bättre förståelse via en förvirringsmatris

Även om du kan få en poängrapport termer genom att skriva ut ovanstående, kan du kanske förstå din modell lättare genom att använda en förvirringsmatris för att hjälpa oss att förstå hur modellen presterar.

🎓 En 'förvirringsmatris' (eller 'felmatris') är en tabell som uttrycker din modells verkliga vs. falska positiva och negativa, och därmed mäter noggrannheten i förutsägelserna.

För att använda en förvirringsmatris, kalla på confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Ta en titt på din modells förvirringsmatris:

array([[162,   4],
       [ 11,  22]])

I Scikit-learn är rader (axel 0) faktiska etiketter och kolumner (axel 1) förutsagda etiketter.

	0	1
0	TN	FP
1	FN	TP

Vad händer här? Låt oss säga att vår modell ombeds att klassificera pumpor mellan två binära kategorier, kategori 'vit' och kategori 'inte-vit'.

Om din modell förutspår en pumpa som inte vit och den tillhör kategorin 'inte-vit' i verkligheten kallar vi det en sann negativ, visat av det övre vänstra numret.
Om din modell förutspår en pumpa som vit och den tillhör kategorin 'inte-vit' i verkligheten kallar vi det en falsk negativ, visat av det nedre vänstra numret.
Om din modell förutspår en pumpa som inte vit och den tillhör kategorin 'vit' i verkligheten kallar vi det en falsk positiv, visat av det övre högra numret.
Om din modell förutspår en pumpa som vit och den tillhör kategorin 'vit' i verkligheten kallar vi det en sann positiv, visat av det nedre högra numret.

Som du kanske har gissat är det att föredra att ha ett större antal sanna positiva och sanna negativa och ett lägre antal falska positiva och falska negativa, vilket innebär att modellen presterar bättre. Hur relaterar förvirringsmatrisen till precision och återkallning? Kom ihåg att klassificeringsrapporten som skrivits ut ovan visade precision (0,85) och återkallning (0,67).

Precision = tp / (tp + fp) = 22 / (22 + 4) = 0,8461538461538461

Återkallning = tp / (tp + fn) = 22 / (22 + 11) = 0,6666666666666666

✅ F: Enligt förvirringsmatrisen, hur presterade modellen? S: Inte dåligt; det finns ett bra antal sanna negativa men också några falska negativa.

Låt oss återbesöka de termer vi såg tidigare med hjälp av förvirringsmatrisens kartläggning av TP/TN och FP/FN:

🎓 Precision: TP/(TP + FP) Andelen relevanta instanser bland de hämtade instanserna (t.ex. vilka etiketter som var korrekt märkta)

🎓 Återkallning: TP/(TP + FN) Andelen relevanta instanser som hämtades, oavsett om de var korrekt märkta eller inte

🎓 f1-score: (2 * precision * återkallning)/(precision + återkallning) Ett viktat genomsnitt av precision och återkallning, där bästa är 1 och sämsta är 0

🎓 Support: Antalet förekomster av varje etikett som hämtats

🎓 Noggrannhet: (TP + TN)/(TP + TN + FP + FN) Procentandelen etiketter som förutsades korrekt för ett urval.

🎓 Makro-genomsnitt: Beräkningen av de oviktade genomsnittliga måtten för varje etikett, utan att ta hänsyn till obalans mellan etiketter.

🎓 Viktat genomsnitt: Beräkningen av de genomsnittliga måtten för varje etikett, med hänsyn till obalans mellan etiketter genom att väga dem efter deras support (antalet sanna instanser för varje etikett).

✅ Kan du tänka dig vilken metrisk du bör fokusera på om du vill att din modell ska minska antalet falska negativa?

Visualisera ROC-kurvan för denna modell

🎥 Klicka på bilden ovan för en kort videogenomgång av ROC-kurvor

Låt oss göra en visualisering till för att se den så kallade 'ROC'-kurvan:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

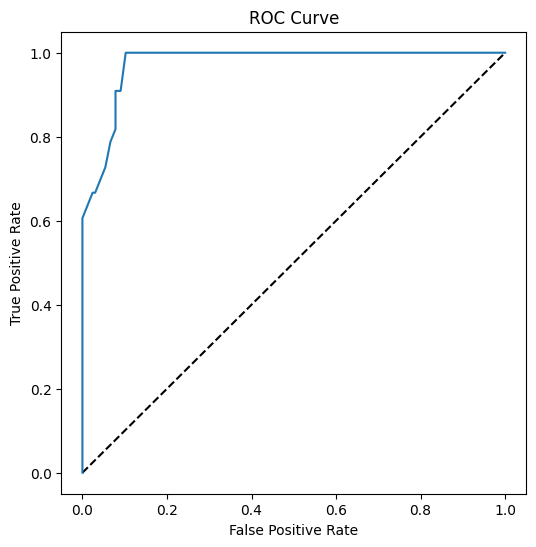
Använd Matplotlib för att plotta modellens Receiving Operating Characteristic eller ROC. ROC-kurvor används ofta för att få en överblick över en klassificerares resultat i termer av dess sanna respektive falska positiva. "ROC-kurvor har vanligtvis den sanna positiva frekvensen på Y-axeln och den falska positiva frekvensen på X-axeln." Därför spelar kurvans branthet och utrymmet mellan mittlinjen och kurvan roll: du vill ha en kurva som snabbt går upp och över linjen. I vårt fall finns det falska positiva i början, och sedan går linjen upp och över korrekt:

Använd slutligen Scikit-learns roc_auc_score API för att beräkna det faktiska 'Area Under the Curve' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Resultatet är 0.9749908725812341. Eftersom AUC sträcker sig från 0 till 1 vill du ha ett högt värde, eftersom en modell som är 100 % korrekt i sina förutsägelser kommer att ha en AUC på 1; i detta fall är modellen ganska bra.

I framtida lektioner om klassificeringar kommer du att lära dig hur du itererar för att förbättra modellens resultat. Men för nu, grattis! Du har avslutat dessa regressionslektioner!

🚀Utmaning

Det finns mycket mer att utforska kring logistisk regression! Men det bästa sättet att lära sig är att experimentera. Hitta en dataset som lämpar sig för denna typ av analys och bygg en modell med den. Vad lär du dig? tips: prova Kaggle för intressanta dataset.

Quiz efter föreläsningen

Granskning & Självstudier

Läs de första sidorna av denna artikel från Stanford om några praktiska användningar för logistisk regression. Fundera på uppgifter som är bättre lämpade för den ena eller andra typen av regressionsuppgifter som vi har studerat hittills. Vad skulle fungera bäst?

Uppgift

Försök denna regression igen

Ansvarsfriskrivning:
Detta dokument har översatts med hjälp av AI-översättningstjänsten Co-op Translator. Även om vi strävar efter noggrannhet, vänligen notera att automatiska översättningar kan innehålla fel eller felaktigheter. Det ursprungliga dokumentet på sitt ursprungliga språk bör betraktas som den auktoritativa källan. För kritisk information rekommenderas professionell mänsklig översättning. Vi ansvarar inte för eventuella missförstånd eller feltolkningar som uppstår vid användning av denna översättning.

22 KiB Raw Permalink Blame History