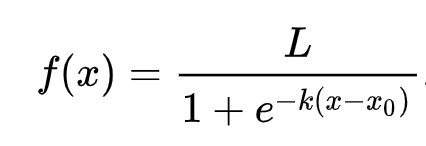31 KiB

Raw Permalink Blame History Unescape Escape

Логистичка регресија за предвиђање категорија

Квиз пре предавања

Ова лекција је доступна и на R!

Увод

У овој последњој лекцији о регресији, једној од основних класичних техника машинског учења, погледаћемо логистичку регресију. Ову технику бисте користили за откривање образаца ради предвиђања бинарних категорија. Да ли је овај слаткиш чоколада или не? Да ли је ова болест заразна или не? Да ли ће овај купац изабрати овај производ или не?

У овој лекцији ћете научити:

Нову библиотеку за визуализацију података
Технике за логистичку регресију

✅ Продубите своје разумевање рада са овом врстом регресије у овом модулу за учење

Предуслов

Радећи са подацима о бундевама, сада смо довољно упознати са њима да схватимо да постоји једна бинарна категорија са којом можемо радити: Боја.

Хајде да направимо модел логистичке регресије да предвидимо, на основу неких варијабли, која боја је вероватно дата бундева (наранџаста 🎃 или бела 👻).

Зашто говоримо о бинарној класификацији у лекцији о регресији? Само ради језичке погодности, јер је логистичка регресија заправо метода класификације, иако заснована на линеарности. Сазнајте више о другим начинима класификације података у следећој групи лекција.

Дефинисање питања

За наше потребе, изразићемо ово као бинарно: 'Бела' или 'Није бела'. У нашем скупу података постоји и категорија 'пругаста', али има мало примера, па је нећемо користити. Ионако нестаје када уклонимо вредности null из скупа података.

🎃 Забавна чињеница: беле бундеве понекад називамо 'духовима'. Нису баш лаке за резбарење, па нису толико популарне као наранџасте, али изгледају занимљиво! Тако да бисмо могли да формулишемо наше питање као: 'Дух' или 'Није дух'. 👻

О логистичкој регресији

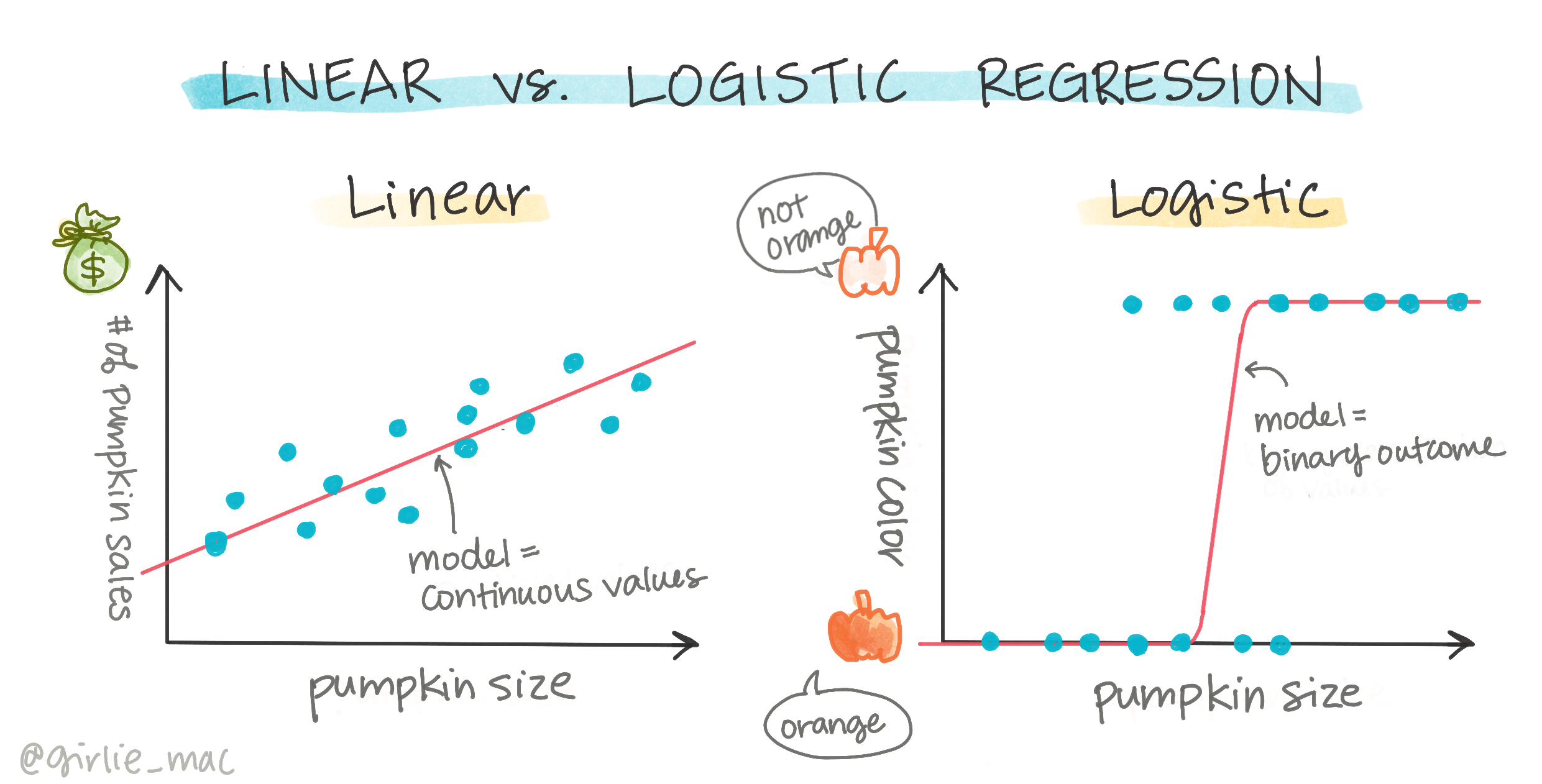
Логистичка регресија се разликује од линеарне регресије, коју сте раније научили, у неколико важних аспеката.

🎥 Кликните на слику изнад за кратак видео преглед логистичке регресије.

Бинарна класификација

Логистичка регресија не нуди исте могућности као линеарна регресија. Прва нуди предвиђање бинарне категорије ("бела или није бела"), док друга може да предвиди континуалне вредности, на пример, на основу порекла бундеве и времена жетве, колико ће њена цена порасти.

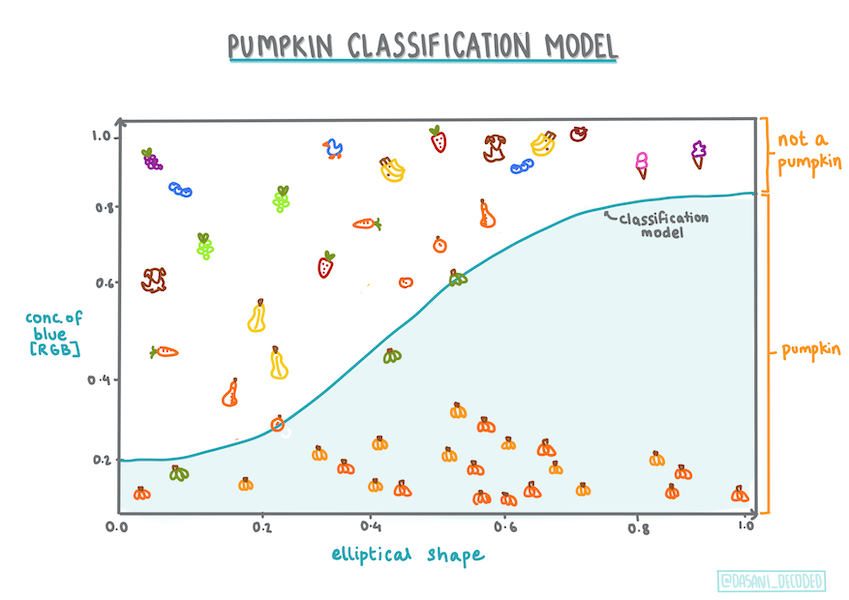
Инфографика од Dasani Madipalli

Друге класификације

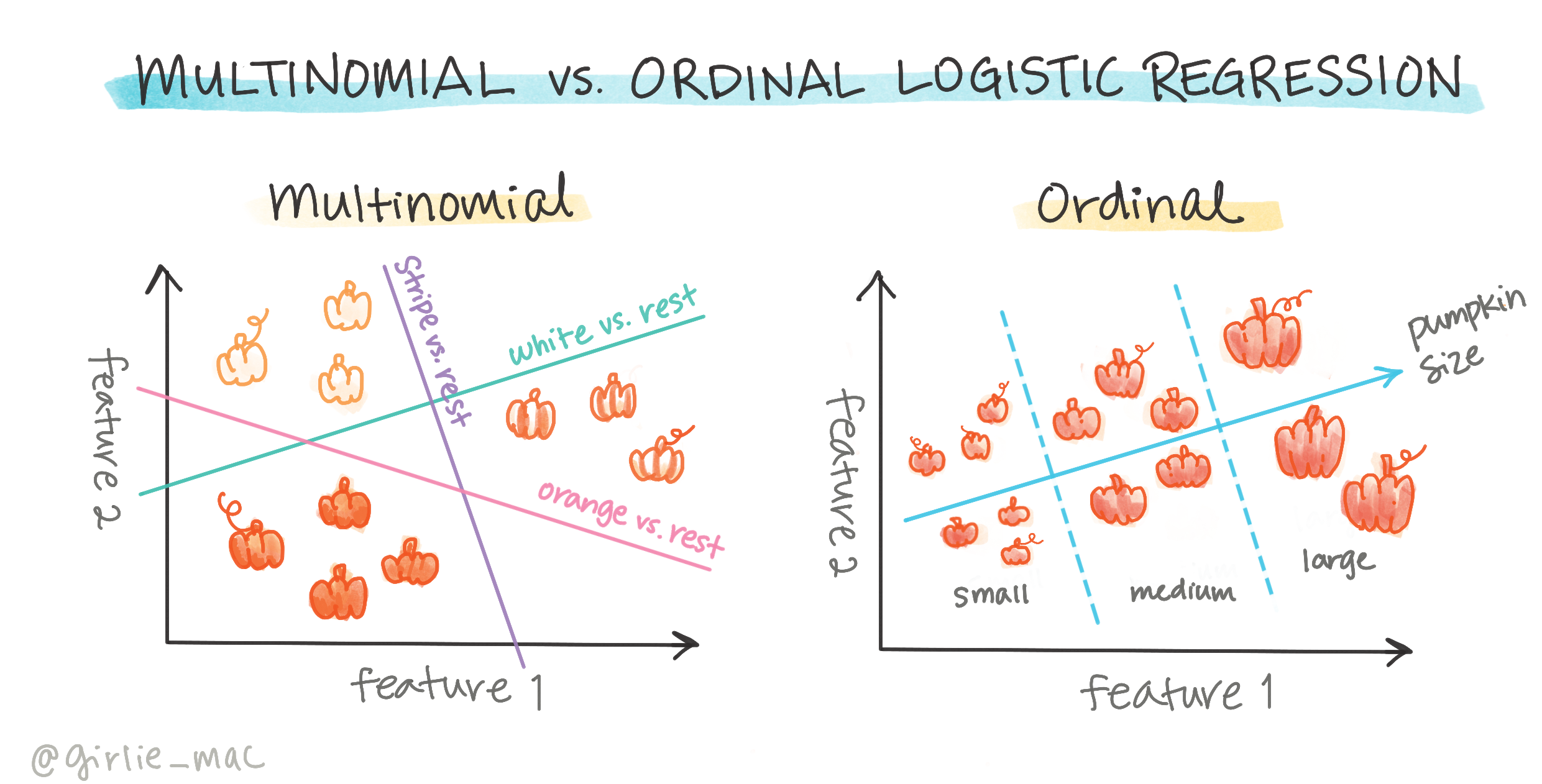
Постоје и друге врсте логистичке регресије, укључујући мултиномијалну и ординалну:

Мултиномијална, која укључује више од једне категорије - "Наранџаста, Бела и Пругаста".
Ординална, која укључује уређене категорије, корисна ако желимо да логички поређамо наше исходе, као што су бундеве које су поређане по ограниченом броју величина (мини, мала, средња, велика, XL, XXL).

Варијабле НЕ морају бити корелисане

Сећате се како је линеарна регресија боље функционисала са више корелисаних варијабли? Логистичка регресија је супротна - варијабле не морају бити усклађене. То одговара овим подацима који имају релативно слабе корелације.

Потребно је много чистих података

Логистичка регресија ће дати прецизније резултате ако користите више података; наш мали скуп података није оптималан за овај задатак, па то имајте на уму.

✅ Размислите о врстама података које би се добро уклопиле у логистичку регресију.

Вежба - уредите податке

Прво, мало очистите податке, уклањајући null вредности и бирајући само неке од колона:

Додајте следећи код:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Увек можете погледати свој нови dataframe:

pumpkins.info

Визуализација - категоријални графикон

До сада сте учитали почетни нотебук са подацима о бундевама и очистили га тако да задржите скуп података који садржи неколико варијабли, укључујући Боја. Хајде да визуализујемо dataframe у нотебуку користећи другу библиотеку: Seaborn, која је изграђена на Matplotlib коју смо раније користили.

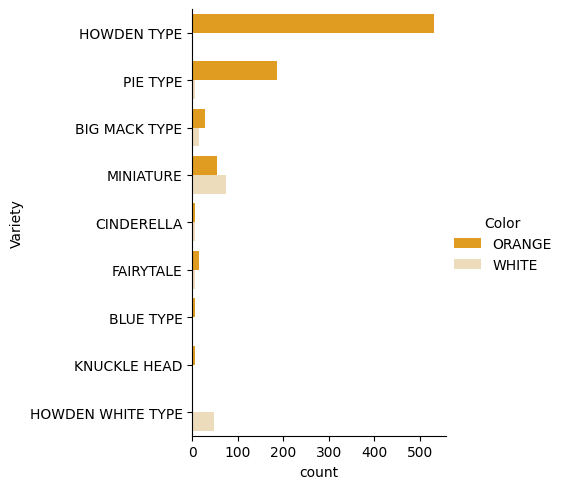
Seaborn нуди неке занимљиве начине за визуализацију ваших података. На пример, можете упоредити дистрибуције података за сваку Сорта и Боја у категоријалном графикону.

Направите такав графикон користећи функцију catplot, користећи наше податке о бундевама pumpkins, и специфицирајући мапирање боја за сваку категорију бундеве (наранџаста или бела):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Посматрајући податке, можете видети како се подаци о боји односе на сорту.

✅ На основу овог категоријалног графикона, које занимљиве анализе можете замислити?

Претпроцесирање података: кодирање карактеристика и ознака

Наш скуп података о бундевама садржи стринг вредности за све своје колоне. Рад са категоријалним подацима је интуитиван за људе, али не и за машине. Алгоритми машинског учења добро функционишу са бројевима. Зато је кодирање веома важан корак у фази претпроцесирања података, јер нам омогућава да категоријалне податке претворимо у нумеричке податке, без губитка информација. Добро кодирање води ка изградњи доброг модела.

За кодирање карактеристика постоје две главне врсте кодера:

Ординални кодер: добро одговара ординалним варијаблама, које су категоријалне варијабле где њихови подаци следе логички редослед, као што је колона Величина артикла у нашем скупу података. Он ствара мапирање тако да је свака категорија представљена бројем, који је редослед категорије у колони.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Категоријални кодер: добро одговара номиналним варијаблама, које су категоријалне варијабле где њихови подаци не следе логички редослед, као што су све карактеристике различите од Величина артикла у нашем скупу података. То је једно-хот кодирање, што значи да је свака категорија представљена бинарном колоном: кодирана варијабла је једнака 1 ако бундева припада тој сорти, а 0 у супротном.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Затим, ColumnTransformer се користи за комбиновање више кодера у један корак и њихово примену на одговарајуће колоне.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

С друге стране, за кодирање ознаке користимо scikit-learn класу LabelEncoder, која је помоћна класа за нормализацију ознака тако да садрже само вредности између 0 и n_classes-1 (овде, 0 и 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Када кодиране карактеристике и ознаке, можемо их спојити у нови dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Које су предности коришћења ординалног кодера за колону Величина артикла?

Анализа односа између варијабли

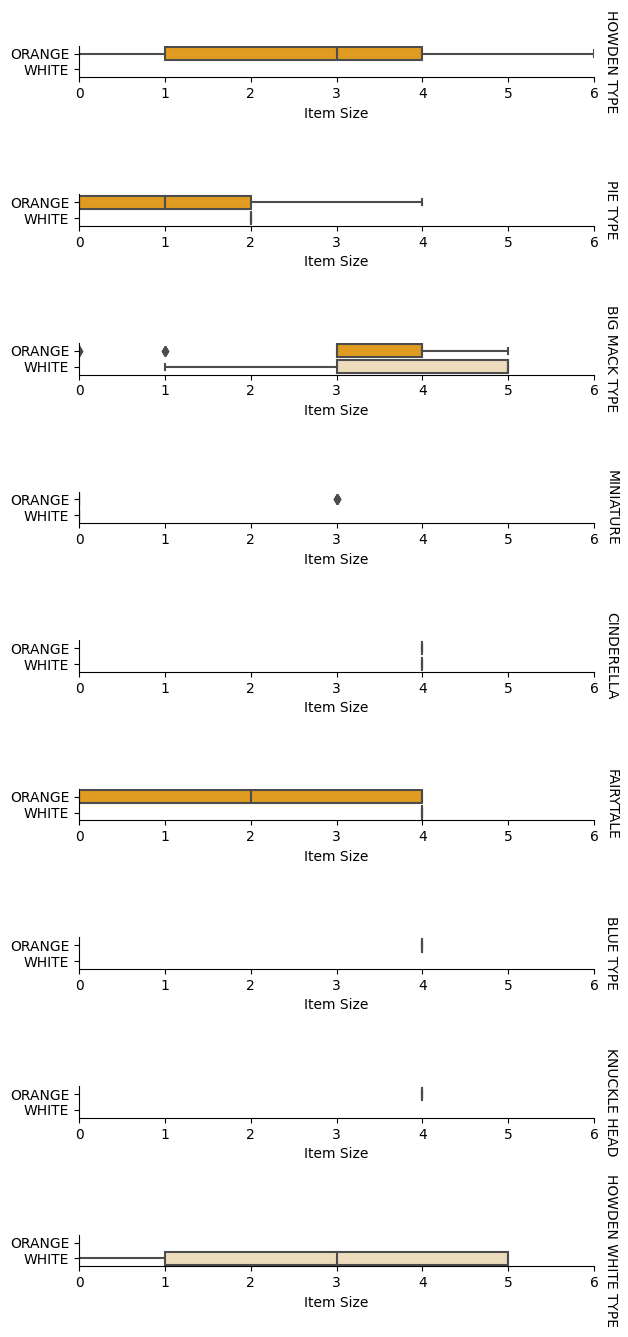
Сада када смо претпроцесирали наше податке, можемо анализирати односе између карактеристика и ознаке како бисмо стекли идеју о томе колико ће модел бити способан да предвиди ознаку на основу карактеристика. Најбољи начин за извођење ове врсте анализе је графичко приказивање података. Поново ћемо користити Seaborn функцију catplot, да визуализујемо односе између Величина артикла, Сорта и Боја у категоријалном графикону. За боље приказивање података користићемо кодиране колоне Величина артикла и некодиране колоне Сорта.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Користите swarm графикон

Пошто је Боја бинарна категорија (Бела или Није), потребан је 'специјализован приступ за визуализацију'. Постоје и други начини за визуализацију односа ове категорије са другим варијаблама.

Можете визуализовати варијабле једну поред друге помоћу Seaborn графикона.

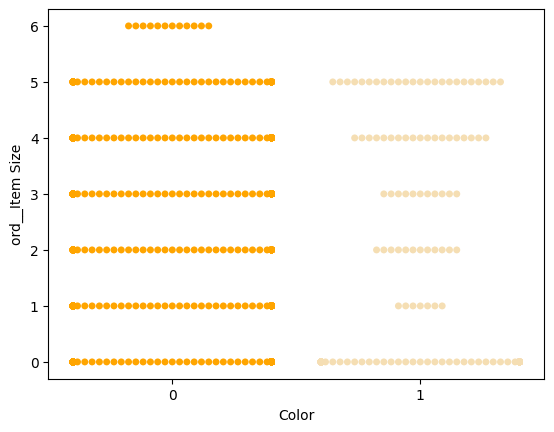
Пробајте 'swarm' графикон да покажете дистрибуцију вредности:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Пазите: горњи код може генерисати упозорење, пошто Seaborn не успева да представи толики број тачака у swarm графикону. Могуће решење је смањење величине маркера, коришћењем параметра 'size'. Међутим, будите свесни да то утиче на читљивост графикона.

🧮 Покажите ми математику

Логистичка регресија се ослања на концепт 'максималне вероватноће' користећи сигмоидне функције. 'Сигмоидна функција' на графикону изгледа као облик слова 'S'. Она узима вредност и мапира је негде између 0 и 1. Њена крива се такође назива 'логистичка крива'. Њена формула изгледа овако:

где се средишња тачка сигмоида налази на x-овој 0 тачки, L је максимална вредност криве, а k је стрмина криве. Ако је исход функције већи од 0.5, ознака у питању ће бити додељена класи '1' бинарног избора. Ако није, биће класификована као '0'.

Направите свој модел

Изградња модела за проналажење ових бинарних класификација је изненађујуће једноставна у Scikit-learn.

🎥 Кликните на слику изнад за кратак видео преглед изградње модела линеарне регресије.

Изаберите варијабле које желите да користите у свом моделу класификације и поделите скуп за тренинг и тестирање позивајући train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Сада можете обучити свој модел, позивајући fit() са својим тренинг подацима, и исписати његов резултат:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Погледајте резултате свог модела. Није лоше, с обзиром на то да имате само око 1000 редова података:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Боље разумевање кроз матрицу конфузије

Иако можете добити извештај о резултатима термини исписивањем горе наведених ставки, можда ћете моћи боље да разумете свој модел користећи матрицу конфузије која нам помаже да разумемо како модел функционише.

🎓 'Матрица конфузије' (или 'матрица грешке') је табела која изражава стварне и лажне позитивне и негативне резултате вашег модела, чиме се процењује тачност предвиђања.

Да бисте користили матрицу конфузије, позовите confusion_matrix():
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)
```
Погледајте матрицу конфузије вашег модела:
```
array([[162,   4],
       [ 11,  22]])
```

У Scikit-learn, редови (осовина 0) су стварне ознаке, а колоне (осовина 1) су предвиђене ознаке.

	0	1
0	TN	FP
1	FN	TP

Шта се овде дешава? Рецимо да се од нашег модела тражи да класификује бундеве између две бинарне категорије, категорије 'бела' и категорије 'није бела'.

Ако ваш модел предвиди да је бундева није бела, а она заиста припада категорији 'није бела', то називамо истинским негативним резултатом, приказаним горњим левим Како се матрица конфузије односи на прецизност и одзив? Запамтите, извештај о класификацији приказан изнад показао је прецизност (0.85) и одзив (0.67).

Прецизност = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Одзив = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ П: Према матрици конфузије, како је модел прошао? О: Није лоше; постоји добар број истинских негативних, али и неколико лажних негативних.

Хајде да поново погледамо термине које смо раније видели уз помоћ мапирања TP/TN и FP/FN у матрици конфузије:

🎓 Прецизност: TP/(TP + FP) Удео релевантних примера међу пронађеним примерима (нпр. који су ознаке добро означене)

🎓 Одзив: TP/(TP + FN) Удео релевантних примера који су пронађени, било добро означени или не

🎓 f1-скор: (2 * прецизност * одзив)/(прецизност + одзив) Тежински просек прецизности и одзива, где је најбољи 1, а најгори 0

🎓 Подршка: Број појављивања сваке ознаке која је пронађена

🎓 Тачност: (TP + TN)/(TP + TN + FP + FN) Проценат ознака које су тачно предвиђене за узорак.

🎓 Макро просек: Израчунавање неутежаног просека метрика за сваку ознаку, без узимања у обзир неравнотеже ознака.

🎓 Тежински просек: Израчунавање просека метрика за сваку ознаку, узимајући у обзир неравнотежу ознака тако што их тежински прилагођава њиховој подршци (броју истинских примера за сваку ознаку).

✅ Можете ли замислити коју метрику треба пратити ако желите да ваш модел смањи број лажних негативних?

Визуализација ROC криве овог модела

🎥 Кликните на слику изнад за кратак видео преглед ROC криве

Хајде да направимо још једну визуализацију да видимо такозвану 'ROC' криву:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

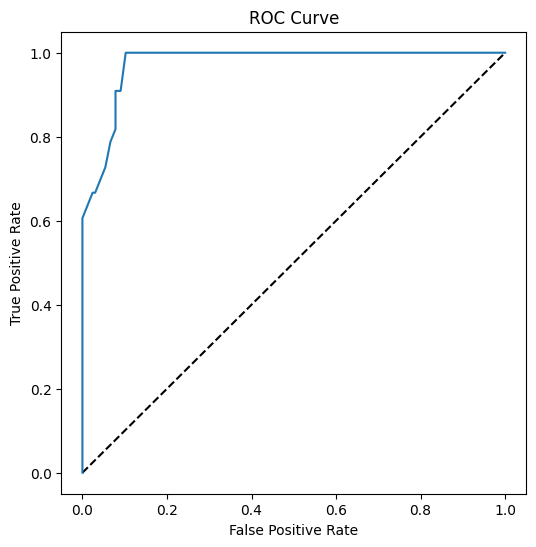
Користећи Matplotlib, нацртајте Receiving Operating Characteristic или ROC модела. ROC криве се често користе за добијање прегледа излазних резултата класификатора у смислу истинских и лажних позитивних. "ROC криве обично приказују стопу истинских позитивних на Y оси, а стопу лажних позитивних на X оси." Дакле, стрмина криве и простор између средишње линије и криве су важни: желите криву која брзо иде горе и преко линије. У нашем случају, постоје лажни позитивни на почетку, а затим линија правилно иде горе и преко:

На крају, користите Scikit-learn roc_auc_score API да израчунате стварну 'Површину испод криве' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Резултат је 0.9749908725812341. С обзиром да AUC варира од 0 до 1, желите велики резултат, јер модел који је 100% тачан у својим предвиђањима имаће AUC од 1; у овом случају, модел је прилично добар.

У будућим лекцијама о класификацијама, научићете како да итеративно побољшате резултате вашег модела. Али за сада, честитамо! Завршили сте ове лекције о регресији!

🚀Изазов

Постоји много више за истраживање у вези са логистичком регресијом! Али најбољи начин за учење је експериментисање. Пронађите скуп података који се добро уклапа у ову врсту анализе и направите модел са њим. Шта сте научили? савет: пробајте Kaggle за занимљиве скупове података.

Квиз после предавања

Преглед и самостално учење

Прочитајте првих неколико страница овог рада са Станфорда о неким практичним применама логистичке регресије. Размислите о задацима који су боље прилагођени једној или другој врсти регресије коју смо до сада проучавали. Шта би најбоље функционисало?

Задатак

Поновно испробавање ове регресије

Одрицање од одговорности:
Овај документ је преведен коришћењем услуге за превођење помоћу вештачке интелигенције Co-op Translator. Иако настојимо да обезбедимо тачност, молимо вас да имате у виду да аутоматски преводи могу садржати грешке или нетачности. Оригинални документ на његовом изворном језику треба сматрати ауторитативним извором. За критичне информације препоручује се професионални превод од стране људи. Не сносимо одговорност за било каква погрешна тумачења или неспоразуме који могу произаћи из коришћења овог превода.

31 KiB Raw Permalink Blame History Unescape Escape