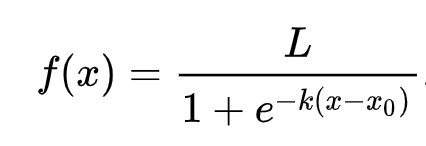23 KiB

Raw Permalink Blame History

Regresja logistyczna do przewidywania kategorii

Quiz przed wykładem

Ta lekcja jest dostępna w R!

Wprowadzenie

W tej ostatniej lekcji dotyczącej regresji, jednej z podstawowych klasycznych technik ML, przyjrzymy się regresji logistycznej. Technika ta pozwala odkrywać wzorce w celu przewidywania binarnych kategorii. Czy ten cukierek to czekolada czy nie? Czy ta choroba jest zakaźna czy nie? Czy ten klient wybierze ten produkt czy nie?

W tej lekcji nauczysz się:

Nowej biblioteki do wizualizacji danych
Technik regresji logistycznej

✅ Pogłęb swoją wiedzę na temat pracy z tego rodzaju regresją w tym module nauki

Wymagania wstępne

Pracując z danymi dotyczącymi dyni, jesteśmy już wystarczająco zaznajomieni z nimi, aby zauważyć, że istnieje jedna binarna kategoria, z którą możemy pracować: Color.

Zbudujmy model regresji logistycznej, aby przewidzieć, na podstawie pewnych zmiennych, jaki kolor ma dana dynia (pomarańczowy 🎃 czy biały 👻).

Dlaczego mówimy o binarnej klasyfikacji w lekcji dotyczącej regresji? Tylko dla wygody językowej, ponieważ regresja logistyczna jest tak naprawdę metodą klasyfikacji, choć opartą na metodach liniowych. Dowiedz się więcej o innych sposobach klasyfikacji danych w kolejnej grupie lekcji.

Zdefiniuj pytanie

Na potrzeby tej lekcji wyrazimy to jako binarną kategorię: 'Biała' lub 'Nie biała'. W naszym zbiorze danych znajduje się również kategoria 'pasiasta', ale jest niewiele jej przypadków, więc jej nie użyjemy. Znika ona zresztą po usunięciu wartości null ze zbioru danych.

🎃 Ciekawostka: białe dynie czasami nazywamy 'dyniami-duchami'. Nie są łatwe do rzeźbienia, więc nie są tak popularne jak pomarańczowe, ale wyglądają bardzo ciekawie! Możemy więc również sformułować nasze pytanie jako: 'Duch' czy 'Nie duch'. 👻

O regresji logistycznej

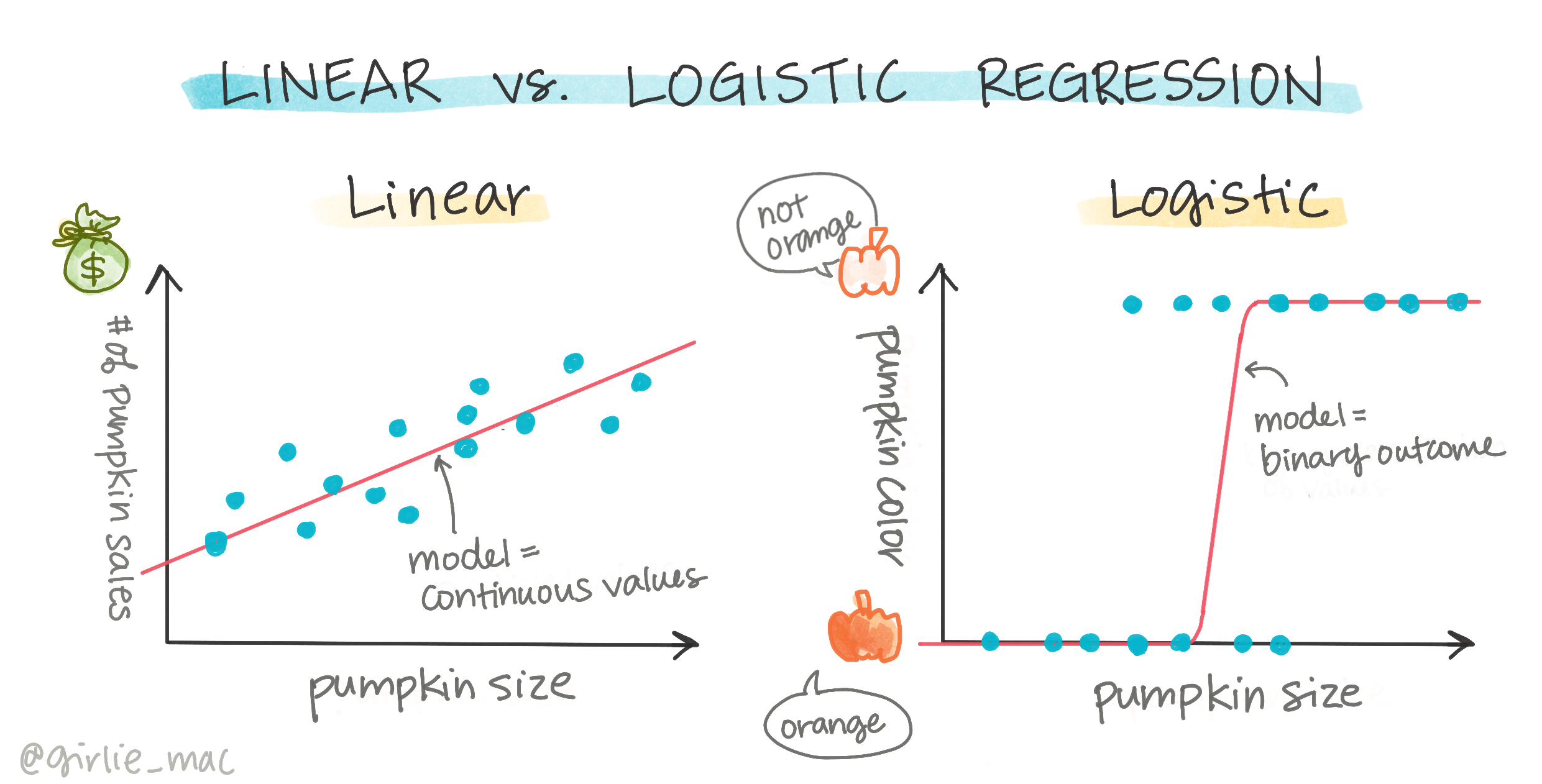
Regresja logistyczna różni się od regresji liniowej, którą poznaliśmy wcześniej, w kilku istotnych aspektach.

🎥 Kliknij obrazek powyżej, aby obejrzeć krótki film o regresji logistycznej.

Klasyfikacja binarna

Regresja logistyczna nie oferuje tych samych funkcji co regresja liniowa. Pierwsza z nich pozwala przewidywać binarne kategorie ("biała czy nie biała"), podczas gdy druga jest w stanie przewidywać wartości ciągłe, na przykład na podstawie pochodzenia dyni i czasu zbioru, o ile wzrośnie jej cena.

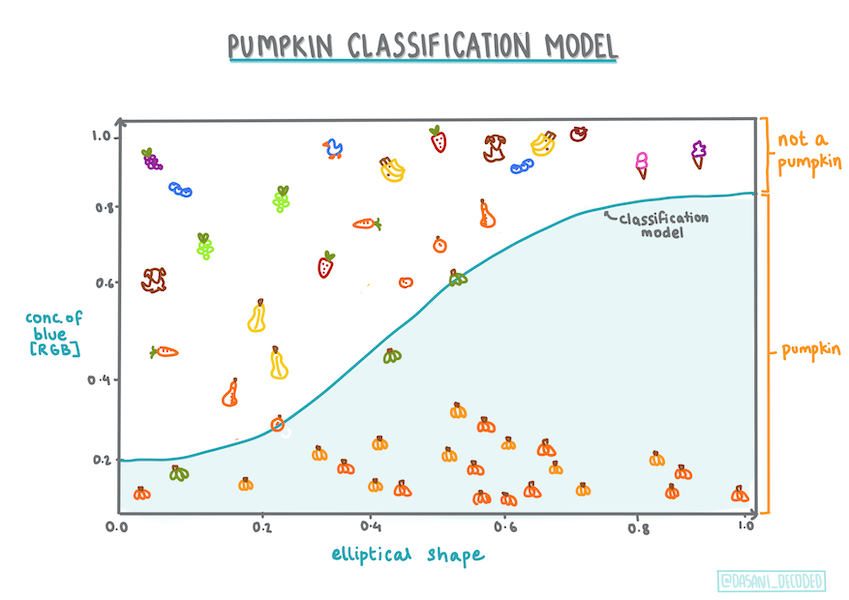
Infografika autorstwa Dasani Madipalli

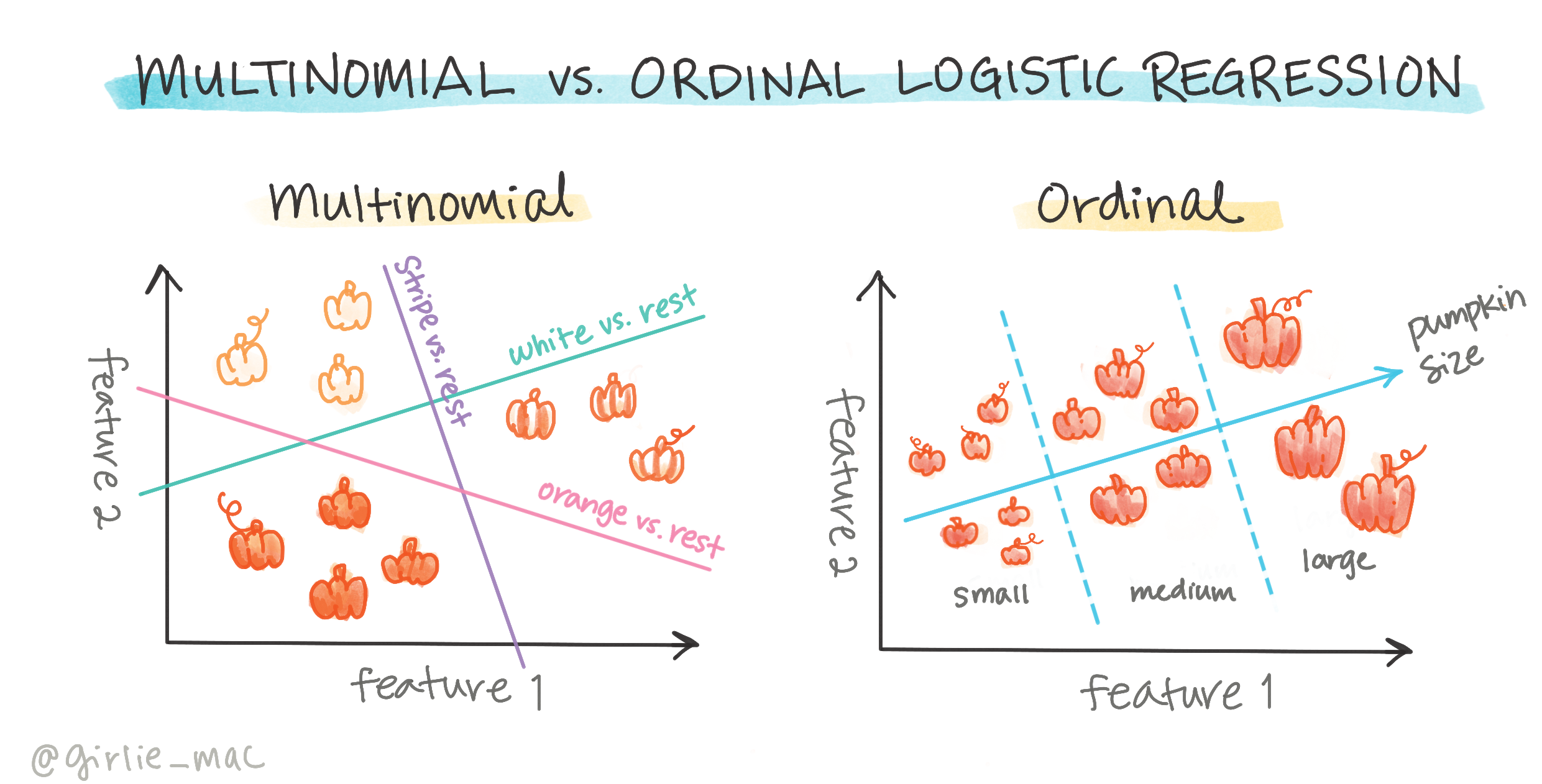
Inne klasyfikacje

Istnieją inne rodzaje regresji logistycznej, w tym wieloklasowa i porządkowa:

Wieloklasowa, która obejmuje więcej niż jedną kategorię - "Pomarańczowa, Biała i Pasiasta".
Porządkowa, która obejmuje uporządkowane kategorie, przydatne, jeśli chcemy uporządkować wyniki logicznie, jak nasze dynie, które są uporządkowane według skończonej liczby rozmiarów (mini, mała, średnia, duża, XL, XXL).

Zmienne NIE muszą być skorelowane

Pamiętasz, jak regresja liniowa działała lepiej z bardziej skorelowanymi zmiennymi? Regresja logistyczna jest odwrotna - zmienne nie muszą być ze sobą powiązane. To działa w przypadku tych danych, które mają raczej słabe korelacje.

Potrzebujesz dużej ilości czystych danych

Regresja logistyczna daje bardziej dokładne wyniki, jeśli używasz większej ilości danych; nasz mały zbiór danych nie jest optymalny do tego zadania, więc miej to na uwadze.

🎥 Kliknij obrazek powyżej, aby obejrzeć krótki film o przygotowaniu danych do regresji liniowej.

✅ Zastanów się, jakie typy danych najlepiej nadają się do regresji logistycznej.

Ćwiczenie - uporządkuj dane

Najpierw trochę oczyść dane, usuwając wartości null i wybierając tylko niektóre kolumny:

Dodaj następujący kod:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Zawsze możesz zajrzeć do swojego nowego dataframe:

pumpkins.info

Wizualizacja - wykres kategorii

Do tej pory załadowałeś notebook startowy z danymi o dyniach i oczyściłeś go, aby zachować zbiór danych zawierający kilka zmiennych, w tym Color. Zwizualizujmy dataframe w notebooku, używając innej biblioteki: Seaborn, która jest zbudowana na Matplotlib, którego używaliśmy wcześniej.

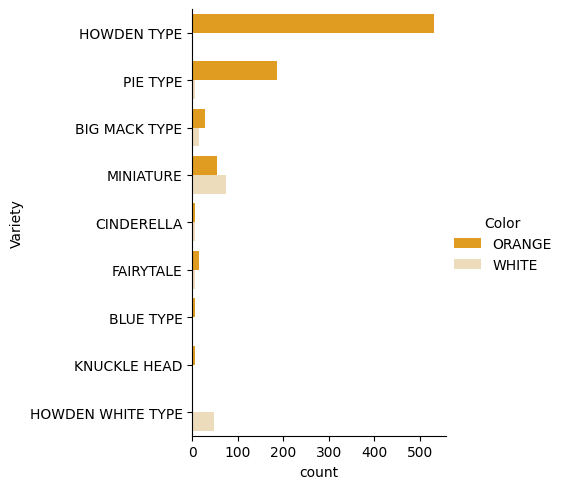
Seaborn oferuje ciekawe sposoby wizualizacji danych. Na przykład możesz porównać rozkłady danych dla każdej Variety i Color na wykresie kategorii.

Utwórz taki wykres, używając funkcji catplot, korzystając z danych o dyniach pumpkins i określając mapowanie kolorów dla każdej kategorii dyni (pomarańczowa lub biała):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Obserwując dane, możesz zobaczyć, jak dane o kolorze odnoszą się do odmiany.

✅ Na podstawie tego wykresu kategorii, jakie interesujące eksploracje możesz sobie wyobrazić?

Przetwarzanie danych: kodowanie cech i etykiet

Nasz zbiór danych o dyniach zawiera wartości tekstowe dla wszystkich swoich kolumn. Praca z danymi kategorycznymi jest intuicyjna dla ludzi, ale nie dla maszyn. Algorytmy uczenia maszynowego dobrze działają z liczbami. Dlatego kodowanie jest bardzo ważnym krokiem w fazie przetwarzania danych, ponieważ pozwala nam zamienić dane kategoryczne na dane numeryczne, nie tracąc żadnych informacji. Dobre kodowanie prowadzi do budowy dobrego modelu.

Dla kodowania cech istnieją dwa główne typy kodowania:

Kodowanie porządkowe: dobrze nadaje się do zmiennych porządkowych, które są zmiennymi kategorycznymi, gdzie ich dane mają logiczne uporządkowanie, jak kolumna Item Size w naszym zbiorze danych. Tworzy mapowanie, w którym każda kategoria jest reprezentowana przez liczbę, która jest kolejnością kategorii w kolumnie.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kodowanie kategoryczne: dobrze nadaje się do zmiennych nominalnych, które są zmiennymi kategorycznymi, gdzie ich dane nie mają logicznego uporządkowania, jak wszystkie cechy inne niż Item Size w naszym zbiorze danych. Jest to kodowanie typu one-hot, co oznacza, że każda kategoria jest reprezentowana przez binarną kolumnę: zakodowana zmienna jest równa 1, jeśli dynia należy do tej odmiany, a 0 w przeciwnym razie.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Następnie ColumnTransformer jest używany do połączenia wielu kodowań w jeden krok i zastosowania ich do odpowiednich kolumn.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Z kolei do kodowania etykiety używamy klasy LabelEncoder z biblioteki scikit-learn, która jest narzędziem do normalizacji etykiet, tak aby zawierały tylko wartości między 0 a n_classes-1 (tutaj, 0 i 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Po zakodowaniu cech i etykiety możemy połączyć je w nowy dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Jakie są zalety używania kodowania porządkowego dla kolumny Item Size?

Analiza relacji między zmiennymi

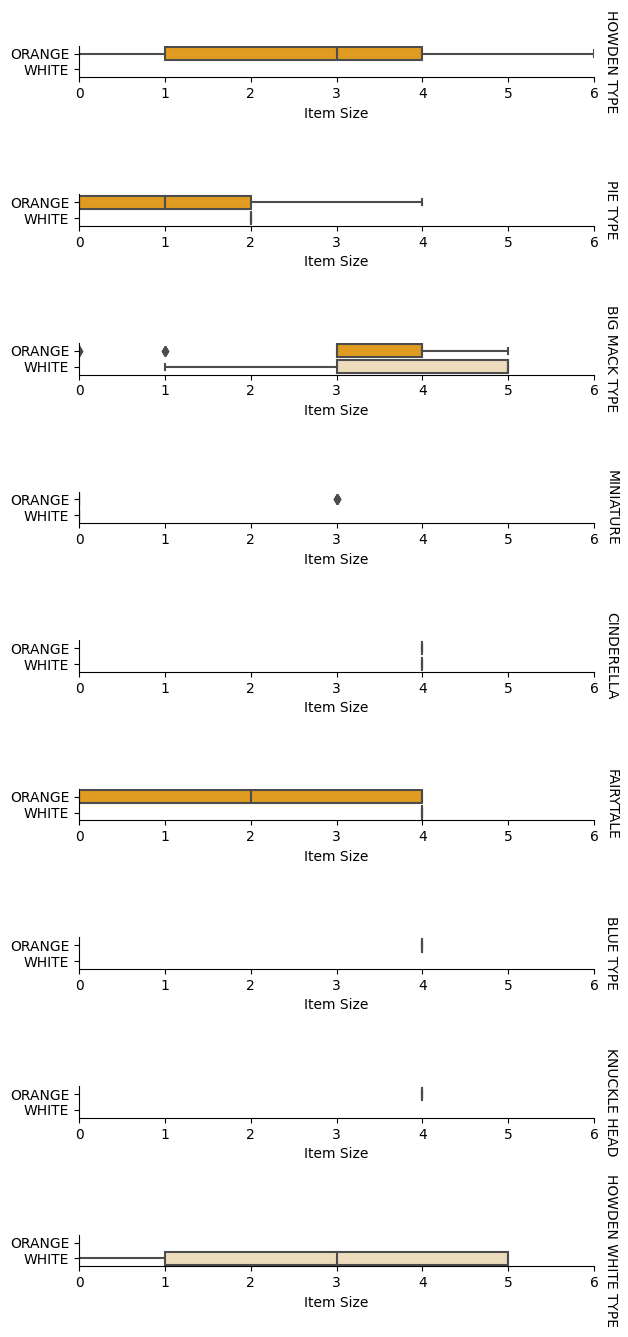
Teraz, gdy przetworzyliśmy nasze dane, możemy przeanalizować relacje między cechami a etykietą, aby zrozumieć, jak dobrze model będzie w stanie przewidzieć etykietę na podstawie cech. Najlepszym sposobem na przeprowadzenie tego rodzaju analizy jest wykreślenie danych. Ponownie użyjemy funkcji catplot z biblioteki Seaborn, aby zwizualizować relacje między Item Size, Variety i Color na wykresie kategorii. Aby lepiej wykreślić dane, użyjemy zakodowanej kolumny Item Size i niezakodowanej kolumny Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Użyj wykresu typu swarm

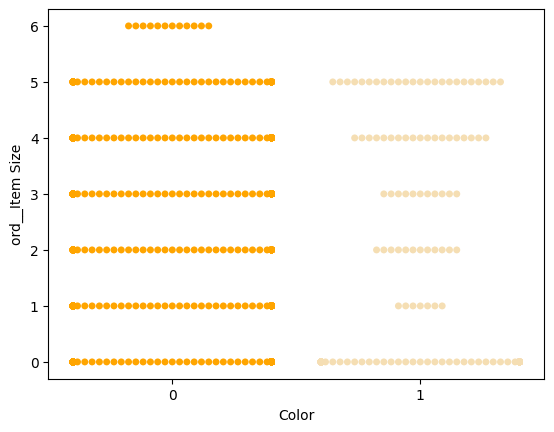
Ponieważ Color jest kategorią binarną (Biała lub Nie), wymaga 'specjalnego podejścia do wizualizacji'. Istnieją inne sposoby wizualizacji relacji tej kategorii z innymi zmiennymi.

Możesz zwizualizować zmienne obok siebie za pomocą wykresów Seaborn.

Wypróbuj wykres typu 'swarm', aby pokazać rozkład wartości:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Uwaga: powyższy kod może wygenerować ostrzeżenie, ponieważ Seaborn nie radzi sobie z reprezentacją takiej ilości punktów danych na wykresie typu swarm. Możliwym rozwiązaniem jest zmniejszenie rozmiaru markerów, używając parametru 'size'. Jednak pamiętaj, że wpływa to na czytelność wykresu.

🧮 Pokaż mi matematykę

Regresja logistyczna opiera się na koncepcji 'maksymalnego prawdopodobieństwa' przy użyciu funkcji sigmoidalnych. 'Funkcja sigmoidalna' na wykresie wygląda jak kształt litery 'S'. Przyjmuje wartość i mapuje ją na zakres między 0 a 1. Jej krzywa jest również nazywana 'krzywą logistyczną'. Jej wzór wygląda tak:

gdzie środek sigmoidy znajduje się w punkcie 0 osi x, L to maksymalna wartość krzywej, a k to stromość krzywej. Jeśli wynik funkcji jest większy niż 0.5, etykieta zostanie przypisana do klasy '1' w binarnym wyborze. W przeciwnym razie zostanie sklasyfikowana jako '0'.

Zbuduj swój model

Budowanie modelu do znajdowania tych klasyfikacji binarnych jest zaskakująco proste w Scikit-learn.

🎥 Kliknij obrazek powyżej, aby obejrzeć krótki film o budowie modelu regresji liniowej.

Wybierz zmienne, które chcesz użyć w swoim modelu klasyfikacji, i podziel zestawy treningowe i testowe, wywołując train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Teraz możesz wytrenować swój model, wywołując fit() z danymi treningowymi, i wydrukować jego wynik:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Spójrz na wyniki swojego modelu. Nie jest źle, biorąc pod uwagę, że masz tylko około 1000 wierszy danych:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Lepsze zrozumienie dzięki macierzy pomyłek

Chociaż możesz uzyskać raport wyników terminy poprzez wydrukowanie powyższych elementów, możesz lepiej zrozumieć swój model, używając macierzy pomyłek, aby pomóc nam zrozumieć, jak model działa.

🎓 'Macierz pomyłek' (lub 'macierz błędów') to tabela, która wyraża prawdziwe vs. fałszywe pozytywy i negatywy twojego modelu, oceniając w ten sposób dokładność przewidywań.

Aby użyć macierzy pomyłek, wywołaj confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Spójrz na macierz pomyłek swojego modelu:

array([[162,   4],
       [ 11,  22]])

W Scikit-learn macierze pomyłek: wiersze (oś 0) to rzeczywiste etykiety, a kolumny (oś 1) to przewidywane etykiety.

	0	1
0	TN	FP
1	FN	TP

Co tu się dzieje? Załóżmy, że nasz model ma za zadanie klasyfikować dynie między dwoma binarnymi kategoriami, kategorią 'biała' i kategorią 'nie biała'.

Jeśli twój model przewiduje dynię jako nie białą, a w rzeczywistości należy ona do kategorii 'nie biała', nazywamy to prawdziwym negatywem, pokazanym przez liczbę w lewym górnym rogu.
Jeśli twój model przewiduje dynię jako białą, a w rzeczywistości należy ona do kategorii 'nie biała', nazywamy to fałszywym negatywem, pokazanym przez liczbę w lewym dolnym rogu.
Jeśli twój model przewiduje dynię jako nie białą, a w rzeczywistości należy ona do kategorii 'biała', nazywamy to fałszywym pozytywem, pokazanym przez liczbę w prawym górnym rogu.
Jeśli twój model przewiduje dynię jako białą, a w rzeczywistości należy ona do kategorii 'biała', nazywamy to prawdziwym pozytywem, pokazanym przez liczbę w prawym dolnym rogu.

Jak się domyślasz, preferowane jest posiadanie większej liczby prawdziwych pozytywów i prawdziwych negatywów oraz mniejszej liczby fałszywych pozytywów i fałszywych negatywów, co oznacza, że model działa lepiej. Jak macierz pomyłek odnosi się do precyzji i czułości? Pamiętaj, że raport klasyfikacji wydrukowany powyżej pokazał precyzję (0,85) i czułość (0,67).

Precyzja = tp / (tp + fp) = 22 / (22 + 4) = 0,8461538461538461

Czułość = tp / (tp + fn) = 22 / (22 + 11) = 0,6666666666666666

✅ P: Jak według macierzy pomyłek poradził sobie model? O: Nieźle; jest sporo prawdziwych negatywów, ale także kilka fałszywych negatywów.

Przyjrzyjmy się jeszcze raz terminom, które poznaliśmy wcześniej, korzystając z mapowania TP/TN i FP/FN w macierzy pomyłek:

🎓 Precyzja: TP/(TP + FP) Ułamek istotnych przypadków wśród odzyskanych przypadków (np. które etykiety zostały dobrze oznaczone).

🎓 Czułość: TP/(TP + FN) Ułamek istotnych przypadków, które zostały odzyskane, niezależnie od tego, czy były dobrze oznaczone, czy nie.

🎓 f1-score: (2 * precyzja * czułość)/(precyzja + czułość) Średnia ważona precyzji i czułości, gdzie najlepszy wynik to 1, a najgorszy to 0.

🎓 Support: Liczba wystąpień każdej odzyskanej etykiety.

🎓 Dokładność: (TP + TN)/(TP + TN + FP + FN) Procent etykiet poprawnie przewidzianych dla próbki.

🎓 Średnia makro: Obliczenie nieważonej średniej metryk dla każdej etykiety, bez uwzględniania nierównowagi etykiet.

🎓 Średnia ważona: Obliczenie średniej metryk dla każdej etykiety, uwzględniające nierównowagę etykiet poprzez ważenie ich wsparciem (liczbą prawdziwych przypadków dla każdej etykiety).

✅ Czy możesz wskazać, którą metrykę należy obserwować, jeśli chcesz, aby Twój model zmniejszył liczbę fałszywych negatywów?

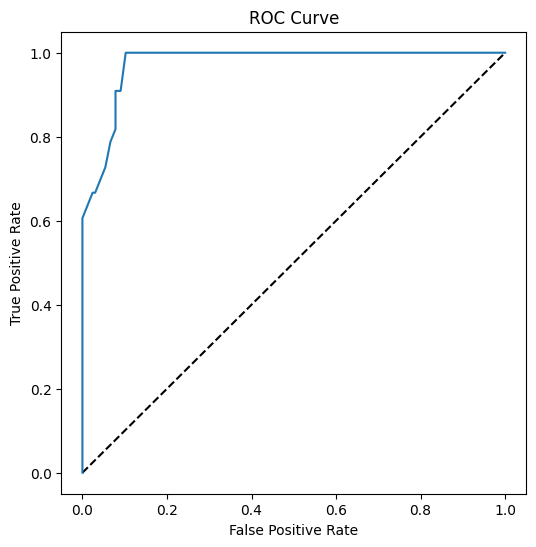
Wizualizacja krzywej ROC dla tego modelu

🎥 Kliknij obrazek powyżej, aby obejrzeć krótki film o krzywych ROC.

Zróbmy jeszcze jedną wizualizację, aby zobaczyć tzw. krzywą 'ROC':

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Korzystając z Matplotlib, narysuj Receiving Operating Characteristic lub ROC modelu. Krzywe ROC są często używane, aby zobaczyć wyniki klasyfikatora w kontekście prawdziwych vs. fałszywych pozytywów. "Krzywe ROC zazwyczaj przedstawiają wskaźnik prawdziwych pozytywów na osi Y i wskaźnik fałszywych pozytywów na osi X." Dlatego stromość krzywej i przestrzeń między linią środkową a krzywą mają znaczenie: chcesz, aby krzywa szybko wznosiła się i oddalała od linii. W naszym przypadku na początku występują fałszywe pozytywy, a następnie linia wznosi się i oddala prawidłowo:

Na koniec użyj API roc_auc_score z biblioteki Scikit-learn, aby obliczyć rzeczywisty 'Obszar pod krzywą' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Wynik to 0.9749908725812341. Biorąc pod uwagę, że AUC mieści się w zakresie od 0 do 1, chcesz uzyskać wysoki wynik, ponieważ model, który jest w 100% poprawny w swoich przewidywaniach, będzie miał AUC równy 1; w tym przypadku model jest całkiem dobry.

W przyszłych lekcjach dotyczących klasyfikacji dowiesz się, jak iteracyjnie poprawiać wyniki swojego modelu. Ale na razie gratulacje! Ukończyłeś te lekcje dotyczące regresji!

🚀Wyzwanie

Regresja logistyczna kryje w sobie jeszcze wiele do odkrycia! Ale najlepszym sposobem na naukę jest eksperymentowanie. Znajdź zbiór danych, który nadaje się do tego typu analizy, i zbuduj na nim model. Czego się nauczysz? Wskazówka: sprawdź Kaggle w poszukiwaniu interesujących zbiorów danych.

Quiz po wykładzie

Przegląd i samodzielna nauka

Przeczytaj pierwsze kilka stron tego artykułu ze Stanfordu na temat praktycznych zastosowań regresji logistycznej. Zastanów się nad zadaniami, które lepiej nadają się do jednego lub drugiego typu zadań regresji, które studiowaliśmy do tej pory. Co sprawdziłoby się najlepiej?

Zadanie

Powtórka z tej regresji

Zastrzeżenie:
Ten dokument został przetłumaczony za pomocą usługi tłumaczenia AI Co-op Translator. Chociaż dokładamy wszelkich starań, aby zapewnić poprawność tłumaczenia, prosimy pamiętać, że automatyczne tłumaczenia mogą zawierać błędy lub nieścisłości. Oryginalny dokument w jego rodzimym języku powinien być uznawany za wiarygodne źródło. W przypadku informacji o kluczowym znaczeniu zaleca się skorzystanie z profesjonalnego tłumaczenia przez człowieka. Nie ponosimy odpowiedzialności za jakiekolwiek nieporozumienia lub błędne interpretacje wynikające z użycia tego tłumaczenia.

23 KiB Raw Permalink Blame History