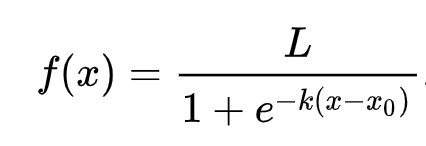22 KiB

Raw Permalink Blame History

Logistische regressie om categorieën te voorspellen

Pre-lecture quiz

Deze les is beschikbaar in R!

Introductie

In deze laatste les over regressie, een van de basis klassieke ML-technieken, gaan we Logistische Regressie bekijken. Je gebruikt deze techniek om patronen te ontdekken en binaire categorieën te voorspellen. Is dit snoep chocolade of niet? Is deze ziekte besmettelijk of niet? Zal deze klant dit product kiezen of niet?

In deze les leer je:

Een nieuwe bibliotheek voor datavisualisatie
Technieken voor logistische regressie

✅ Verdiep je begrip van het werken met dit type regressie in deze Learn module

Vereisten

Na gewerkt te hebben met de pompoendata, zijn we nu voldoende bekend met de dataset om te beseffen dat er één binaire categorie is waarmee we kunnen werken: Color.

Laten we een logistisch regressiemodel bouwen om te voorspellen, gegeven enkele variabelen, welke kleur een bepaalde pompoen waarschijnlijk zal hebben (oranje 🎃 of wit 👻).

Waarom bespreken we binaire classificatie in een lesgroep over regressie? Alleen om taalkundige redenen, aangezien logistische regressie eigenlijk een classificatiemethode is, zij het een lineaire. Leer meer over andere manieren om data te classificeren in de volgende lesgroep.

Definieer de vraag

Voor onze doeleinden zullen we dit uitdrukken als een binair: 'Wit' of 'Niet Wit'. Er is ook een 'gestreepte' categorie in onze dataset, maar er zijn weinig gevallen van, dus we zullen deze niet gebruiken. Het verdwijnt sowieso zodra we null-waarden uit de dataset verwijderen.

🎃 Leuk weetje: we noemen witte pompoenen soms 'spookpompoenen'. Ze zijn niet erg gemakkelijk te snijden, dus ze zijn niet zo populair als de oranje, maar ze zien er wel cool uit! We zouden onze vraag dus ook kunnen herformuleren als: 'Spook' of 'Niet Spook'. 👻

Over logistische regressie

Logistische regressie verschilt op een aantal belangrijke manieren van lineaire regressie, die je eerder hebt geleerd.

🎥 Klik op de afbeelding hierboven voor een korte video-overzicht van logistische regressie.

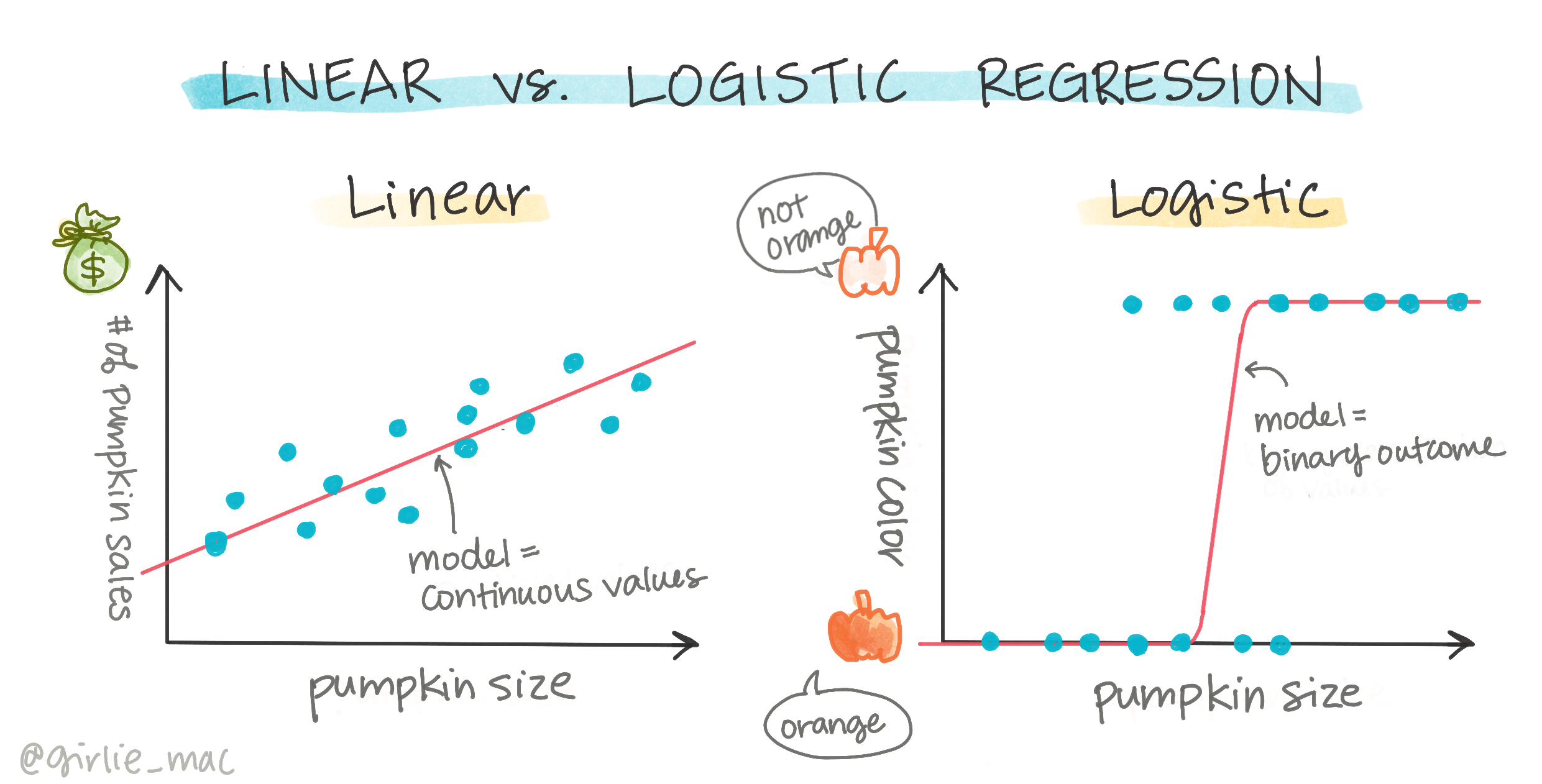
Binaire classificatie

Logistische regressie biedt niet dezelfde functies als lineaire regressie. De eerste biedt een voorspelling over een binaire categorie ("wit of niet wit"), terwijl de laatste in staat is om continue waarden te voorspellen, bijvoorbeeld gegeven de oorsprong van een pompoen en de oogsttijd, hoeveel de prijs zal stijgen.

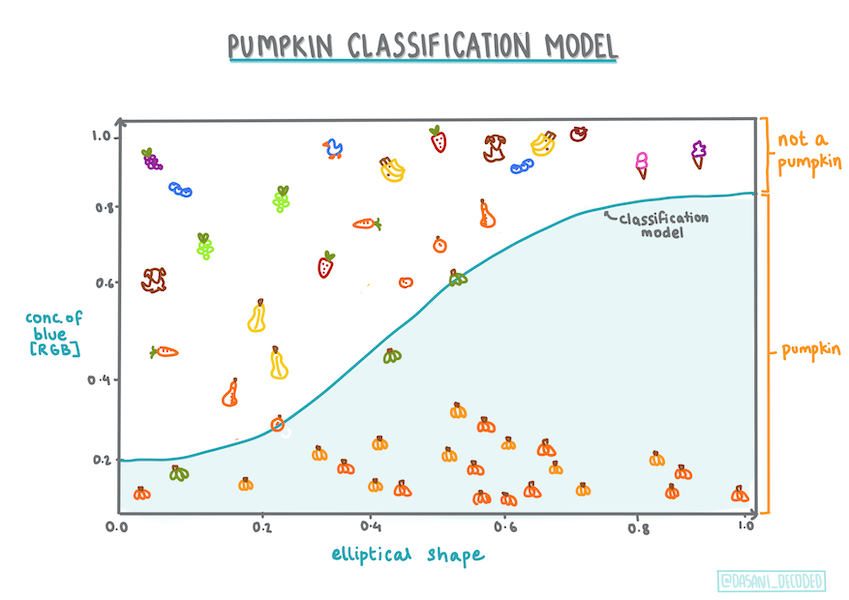
Infographic door Dasani Madipalli

Andere classificaties

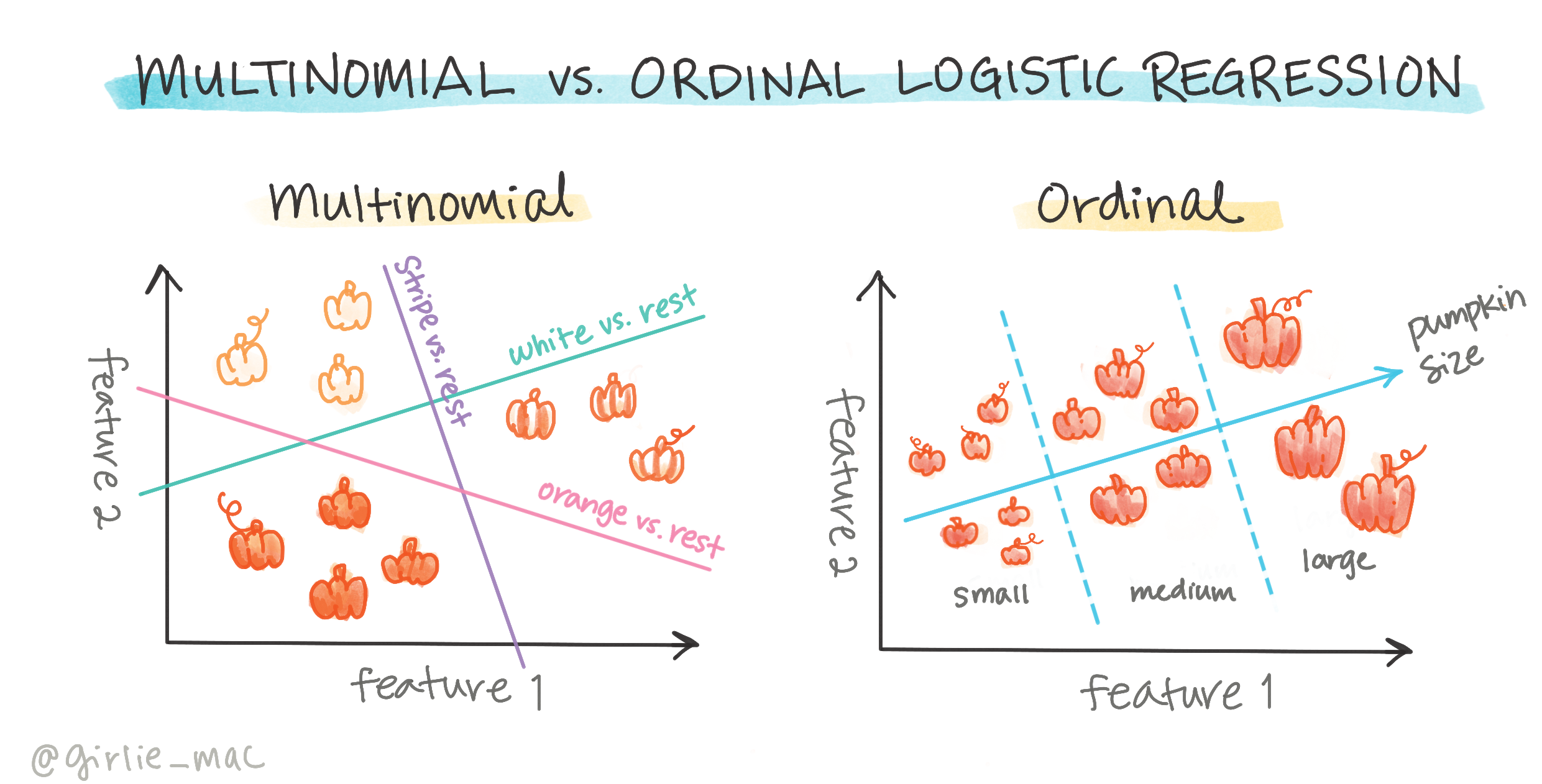
Er zijn andere soorten logistische regressie, waaronder multinomiaal en ordinaal:

Multinomiaal, waarbij er meer dan één categorie is - "Oranje, Wit en Gestreept".
Ordinaal, waarbij geordende categorieën betrokken zijn, nuttig als we onze uitkomsten logisch willen ordenen, zoals onze pompoenen die zijn geordend op een eindig aantal maten (mini, sm, med, lg, xl, xxl).

Variabelen hoeven NIET te correleren

Weet je nog hoe lineaire regressie beter werkte met meer gecorreleerde variabelen? Logistische regressie is het tegenovergestelde - de variabelen hoeven niet te correleren. Dat werkt voor deze data, die enigszins zwakke correlaties heeft.

Je hebt veel schone data nodig

Logistische regressie geeft nauwkeurigere resultaten als je meer data gebruikt; onze kleine dataset is niet optimaal voor deze taak, dus houd dat in gedachten.

🎥 Klik op de afbeelding hierboven voor een korte video-overzicht van het voorbereiden van data voor lineaire regressie.

✅ Denk na over de soorten data die zich goed lenen voor logistische regressie.

Oefening - maak de data schoon

Maak eerst de data een beetje schoon door null-waarden te verwijderen en alleen enkele kolommen te selecteren:

Voeg de volgende code toe:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Je kunt altijd een kijkje nemen in je nieuwe dataframe:

pumpkins.info

Visualisatie - categorische plot

Je hebt inmiddels het starter notebook geladen met pompoendata en deze schoongemaakt om een dataset te behouden met enkele variabelen, waaronder Color. Laten we de dataframe visualiseren in het notebook met een andere bibliotheek: Seaborn, die is gebouwd op Matplotlib, die we eerder hebben gebruikt.

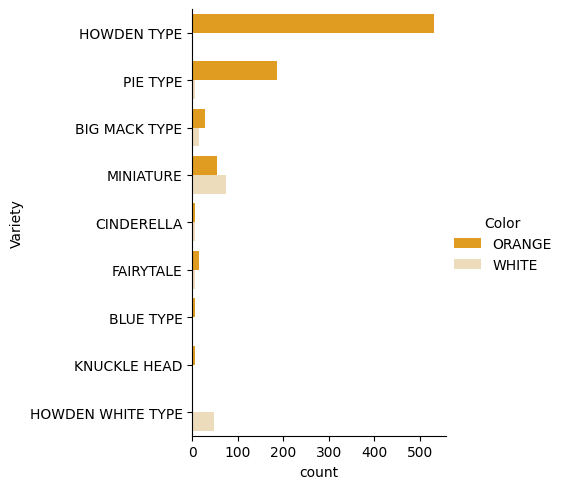
Seaborn biedt enkele handige manieren om je data te visualiseren. Je kunt bijvoorbeeld de verdelingen van de data vergelijken voor elke Variety en Color in een categorische plot.

Maak zo'n plot door de functie catplot te gebruiken, met onze pompoendata pumpkins, en een kleurmapping te specificeren voor elke pompoencategorie (oranje of wit):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Door de data te observeren, kun je zien hoe de Color-data zich verhoudt tot Variety.

✅ Gegeven deze categorische plot, welke interessante verkenningen kun je bedenken?

Data pre-processing: feature- en labelcodering

Onze pompoendataset bevat stringwaarden voor al zijn kolommen. Werken met categorische data is intuïtief voor mensen, maar niet voor machines. Machine learning-algoritmen werken goed met cijfers. Daarom is codering een zeer belangrijke stap in de data pre-processing fase, omdat het ons in staat stelt categorische data om te zetten in numerieke data, zonder informatie te verliezen. Goede codering leidt tot het bouwen van een goed model.

Voor feature-codering zijn er twee hoofdtypen encoders:

Ordinale encoder: geschikt voor ordinale variabelen, die categorische variabelen zijn waarbij hun data een logische volgorde volgt, zoals de Item Size-kolom in onze dataset. Het creëert een mapping zodat elke categorie wordt weergegeven door een nummer, dat de volgorde van de categorie in de kolom is.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Categorische encoder: geschikt voor nominale variabelen, die categorische variabelen zijn waarbij hun data geen logische volgorde volgt, zoals alle features behalve Item Size in onze dataset. Het is een one-hot encoding, wat betekent dat elke categorie wordt weergegeven door een binaire kolom: de gecodeerde variabele is gelijk aan 1 als de pompoen tot die Variety behoort en anders 0.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Daarna wordt ColumnTransformer gebruikt om meerdere encoders te combineren in één stap en deze toe te passen op de juiste kolommen.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Voor het coderen van het label gebruiken we de scikit-learn LabelEncoder-klasse, een hulpprogrammaklasse om labels te normaliseren zodat ze alleen waarden bevatten tussen 0 en n_classes-1 (hier, 0 en 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Zodra we de features en het label hebben gecodeerd, kunnen we ze samenvoegen in een nieuwe dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Wat zijn de voordelen van het gebruik van een ordinale encoder voor de Item Size-kolom?

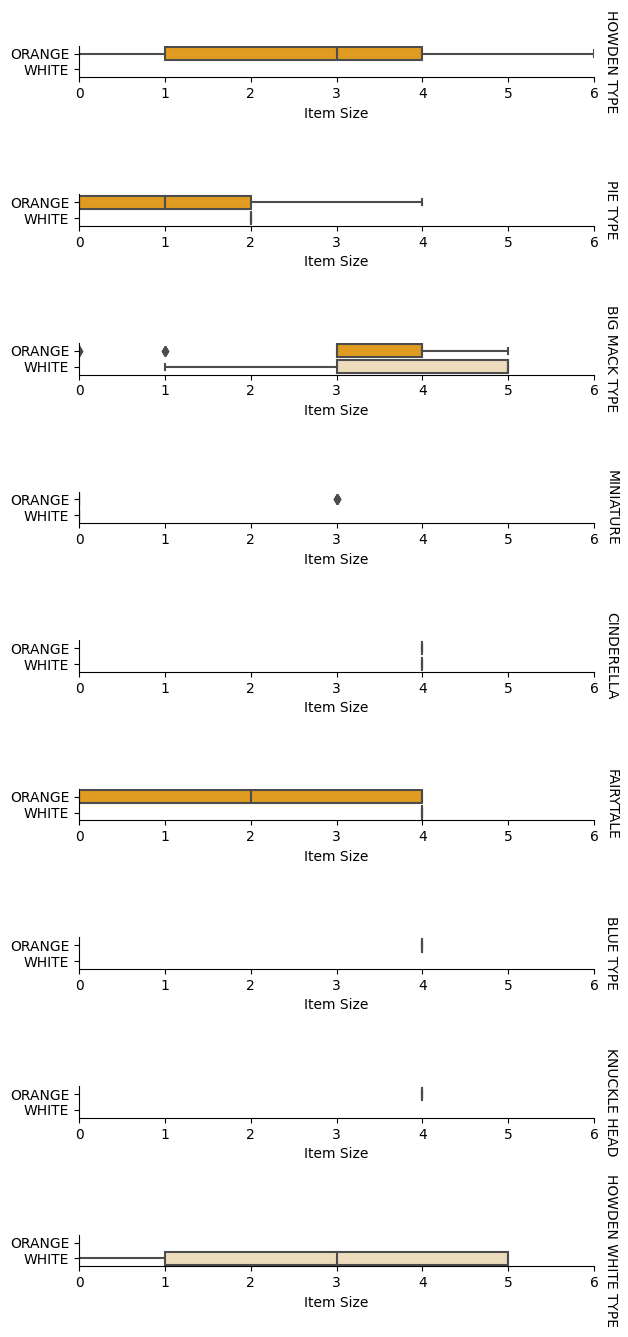
Analyseer relaties tussen variabelen

Nu we onze data hebben voorbewerkt, kunnen we de relaties tussen de features en het label analyseren om een idee te krijgen van hoe goed het model het label kan voorspellen op basis van de features. De beste manier om dit soort analyses uit te voeren is door de data te plotten. We gebruiken opnieuw de Seaborn catplot-functie om de relaties tussen Item Size, Variety en Color in een categorische plot te visualiseren. Om de data beter te plotten, gebruiken we de gecodeerde Item Size-kolom en de ongecodeerde Variety-kolom.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Gebruik een swarm plot

Aangezien Color een binaire categorie is (Wit of Niet), heeft het 'een gespecialiseerde aanpak nodig voor visualisatie'. Er zijn andere manieren om de relatie van deze categorie met andere variabelen te visualiseren.

Je kunt variabelen naast elkaar visualiseren met Seaborn-plots.

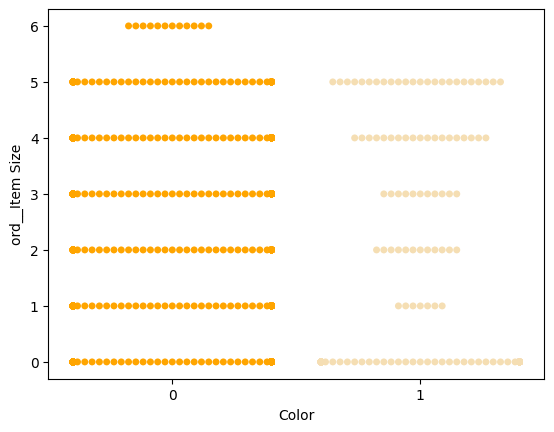
Probeer een 'swarm'-plot om de verdeling van waarden te tonen:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Let op: de bovenstaande code kan een waarschuwing genereren, omdat Seaborn moeite heeft om zo'n hoeveelheid datapunten in een swarm plot weer te geven. Een mogelijke oplossing is het verkleinen van de marker door de 'size'-parameter te gebruiken. Houd er echter rekening mee dat dit de leesbaarheid van de plot beïnvloedt.

🧮 Laat me de wiskunde zien

Logistische regressie is gebaseerd op het concept van 'maximum likelihood' met behulp van sigmoidfuncties. Een 'Sigmoidfunctie' op een plot ziet eruit als een 'S'-vorm. Het neemt een waarde en zet deze om naar ergens tussen 0 en 1. De curve wordt ook wel een 'logistische curve' genoemd. De formule ziet er zo uit:

waarbij het middenpunt van de sigmoid zich bevindt op het 0-punt van x, L de maximale waarde van de curve is, en k de steilheid van de curve is. Als de uitkomst van de functie meer dan 0,5 is, krijgt het betreffende label de klasse '1' van de binaire keuze. Zo niet, dan wordt het geclassificeerd als '0'.

Bouw je model

Het bouwen van een model om deze binaire classificatie te vinden is verrassend eenvoudig in Scikit-learn.

🎥 Klik op de afbeelding hierboven voor een korte video-overzicht van het bouwen van een lineair regressiemodel.

Selecteer de variabelen die je wilt gebruiken in je classificatiemodel en splits de trainings- en testsets door train_test_split() aan te roepen:

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Nu kun je je model trainen door fit() aan te roepen met je trainingsdata en het resultaat af te drukken:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Bekijk het scorebord van je model. Het is niet slecht, gezien je slechts ongeveer 1000 rijen data hebt:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Betere begrip via een confusion matrix

Hoewel je een scorebordrapport kunt krijgen termen door de bovenstaande items af te drukken, kun je je model mogelijk beter begrijpen door een confusion matrix te gebruiken om ons te helpen begrijpen hoe het model presteert.

🎓 Een 'confusion matrix' (of 'error matrix') is een tabel die de echte versus valse positieven en negatieven van je model uitdrukt, en daarmee de nauwkeurigheid van voorspellingen meet.

Om een confusion matrix te gebruiken, roep confusion_matrix() aan:

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Bekijk de confusion matrix van je model:

array([[162,   4],
       [ 11,  22]])

In Scikit-learn zijn de rijen (as 0) de werkelijke labels en de kolommen (as 1) de voorspelde labels.

	0	1
0	TN	FP
1	FN	TP

Wat gebeurt er hier? Stel dat ons model wordt gevraagd om pompoenen te classificeren tussen twee binaire categorieën, categorie 'wit' en categorie 'niet-wit'.

Als je model een pompoen voorspelt als niet wit en deze behoort in werkelijkheid tot categorie 'niet-wit', noemen we dit een true negative, weergegeven door het getal linksboven.
Als je model een pompoen voorspelt als wit en deze behoort in werkelijkheid tot categorie 'niet-wit', noemen we dit een false negative, weergegeven door het getal linksonder.
Als je model een pompoen voorspelt als niet wit en deze behoort in werkelijkheid tot categorie 'wit', noemen we dit een false positive, weergegeven door het getal rechtsboven.
Als je model een pompoen voorspelt als wit en deze behoort in werkelijkheid tot categorie 'wit', noemen we dit een true positive, weergegeven door het getal rechtsonder.

Zoals je misschien hebt geraden, is het beter om een groter aantal true positives en true negatives te hebben en een lager aantal false positives en false negatives, wat impliceert dat het model beter presteert. Hoe hangt de confusion matrix samen met precisie en recall? Onthoud dat het classificatierapport hierboven precisie (0.85) en recall (0.67) liet zien.

Precisie = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Recall = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ V: Volgens de confusion matrix, hoe heeft het model gepresteerd? A: Niet slecht; er zijn een goed aantal true negatives, maar ook enkele false negatives.

Laten we de termen die we eerder zagen opnieuw bekijken met behulp van de mapping van TP/TN en FP/FN in de confusion matrix:

🎓 Precisie: TP/(TP + FP) Het aandeel relevante gevallen onder de opgehaalde gevallen (bijvoorbeeld welke labels correct gelabeld zijn).

🎓 Recall: TP/(TP + FN) Het aandeel relevante gevallen dat is opgehaald, ongeacht of ze correct gelabeld zijn.

🎓 f1-score: (2 * precisie * recall)/(precisie + recall) Een gewogen gemiddelde van precisie en recall, waarbij 1 het beste is en 0 het slechtste.

🎓 Support: Het aantal keren dat elk label is opgehaald.

🎓 Nauwkeurigheid: (TP + TN)/(TP + TN + FP + FN) Het percentage labels dat correct is voorspeld voor een steekproef.

🎓 Macro Gemiddelde: De berekening van de niet-gewogen gemiddelde metrics voor elk label, zonder rekening te houden met label-ongelijkheid.

🎓 Gewogen Gemiddelde: De berekening van de gemiddelde metrics voor elk label, waarbij rekening wordt gehouden met label-ongelijkheid door ze te wegen op basis van hun support (het aantal echte gevallen voor elk label).

✅ Kun je bedenken welke metric je in de gaten moet houden als je wilt dat je model het aantal false negatives vermindert?

Visualiseer de ROC-curve van dit model

🎥 Klik op de afbeelding hierboven voor een korte video-overzicht van ROC-curves

Laten we nog een visualisatie maken om de zogenaamde 'ROC'-curve te bekijken:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

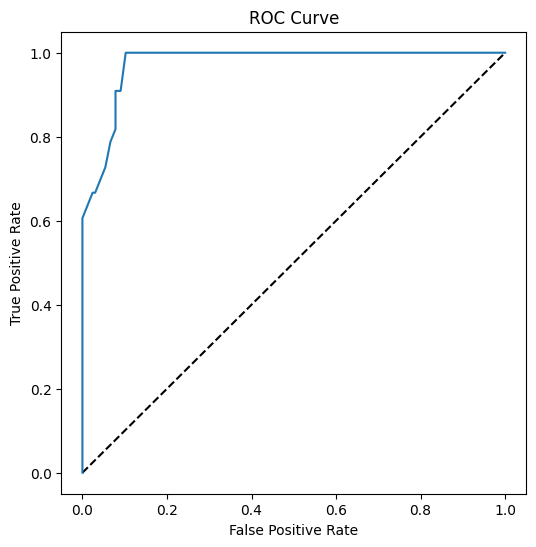
Gebruik Matplotlib om de Receiving Operating Characteristic of ROC van het model te plotten. ROC-curves worden vaak gebruikt om een beeld te krijgen van de output van een classifier in termen van true vs. false positives. "ROC-curves hebben meestal de true positive rate op de Y-as en de false positive rate op de X-as." Dus de steilheid van de curve en de ruimte tussen de middenlijn en de curve zijn belangrijk: je wilt een curve die snel omhoog gaat en over de lijn heen buigt. In ons geval zijn er false positives in het begin, en daarna buigt de lijn correct omhoog en over:

Gebruik ten slotte de roc_auc_score API van Scikit-learn om de daadwerkelijke 'Area Under the Curve' (AUC) te berekenen:

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Het resultaat is 0.9749908725812341. Aangezien de AUC varieert van 0 tot 1, wil je een hoge score, omdat een model dat 100% correct is in zijn voorspellingen een AUC van 1 zal hebben; in dit geval is het model best goed.

In toekomstige lessen over classificaties leer je hoe je iteratief de scores van je model kunt verbeteren. Maar voor nu, gefeliciteerd! Je hebt deze lessen over regressie voltooid!

🚀Uitdaging

Er is nog veel meer te ontdekken over logistic regression! Maar de beste manier om te leren is door te experimenteren. Zoek een dataset die geschikt is voor dit type analyse en bouw er een model mee. Wat leer je? Tip: probeer Kaggle voor interessante datasets.

Quiz na de les

Review & Zelfstudie

Lees de eerste paar pagina's van dit paper van Stanford over enkele praktische toepassingen van logistic regression. Denk na over taken die beter geschikt zijn voor het ene of het andere type regressietaken die we tot nu toe hebben bestudeerd. Wat zou het beste werken?

Opdracht

Probeer deze regressie opnieuw

Disclaimer:
Dit document is vertaald met behulp van de AI-vertalingsservice Co-op Translator. Hoewel we streven naar nauwkeurigheid, dient u zich ervan bewust te zijn dat geautomatiseerde vertalingen fouten of onnauwkeurigheden kunnen bevatten. Het originele document in zijn oorspronkelijke taal moet worden beschouwd als de gezaghebbende bron. Voor cruciale informatie wordt professionele menselijke vertaling aanbevolen. Wij zijn niet aansprakelijk voor eventuele misverstanden of verkeerde interpretaties die voortvloeien uit het gebruik van deze vertaling.

22 KiB Raw Permalink Blame History