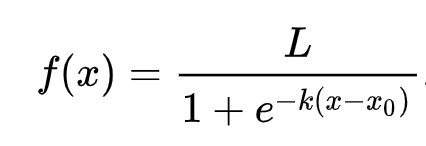23 KiB

Raw Permalink Blame History

Regressione logistica per prevedere categorie

Quiz pre-lezione

Questa lezione è disponibile in R!

Introduzione

In questa ultima lezione sulla regressione, una delle tecniche classiche di ML di base, esamineremo la regressione logistica. Questa tecnica viene utilizzata per scoprire schemi e prevedere categorie binarie. Questa caramella è cioccolato o no? Questa malattia è contagiosa o no? Questo cliente sceglierà questo prodotto o no?

In questa lezione imparerai:

Una nuova libreria per la visualizzazione dei dati
Tecniche per la regressione logistica

✅ Approfondisci la tua comprensione di questo tipo di regressione in questo modulo di apprendimento

Prerequisiti

Avendo lavorato con i dati delle zucche, ora siamo abbastanza familiari con essi da capire che c'è una categoria binaria su cui possiamo lavorare: Color.

Costruiamo un modello di regressione logistica per prevedere, date alcune variabili, di che colore è probabile che sia una determinata zucca (arancione 🎃 o bianca 👻).

Perché stiamo parlando di classificazione binaria in una lezione sulla regressione? Solo per comodità linguistica, poiché la regressione logistica è in realtà un metodo di classificazione, sebbene basato su un approccio lineare. Scopri altri modi per classificare i dati nel prossimo gruppo di lezioni.

Definire la domanda

Per i nostri scopi, esprimeremo questa domanda come un binario: 'Bianca' o 'Non Bianca'. Nel nostro dataset c'è anche una categoria 'a strisce', ma ci sono pochi esempi di essa, quindi non la utilizzeremo. Comunque, scompare una volta che rimuoviamo i valori nulli dal dataset.

🎃 Curiosità: a volte chiamiamo le zucche bianche 'zucche fantasma'. Non sono molto facili da intagliare, quindi non sono popolari come quelle arancioni, ma hanno un aspetto interessante! Potremmo quindi riformulare la nostra domanda come: 'Fantasma' o 'Non Fantasma'. 👻

Sulla regressione logistica

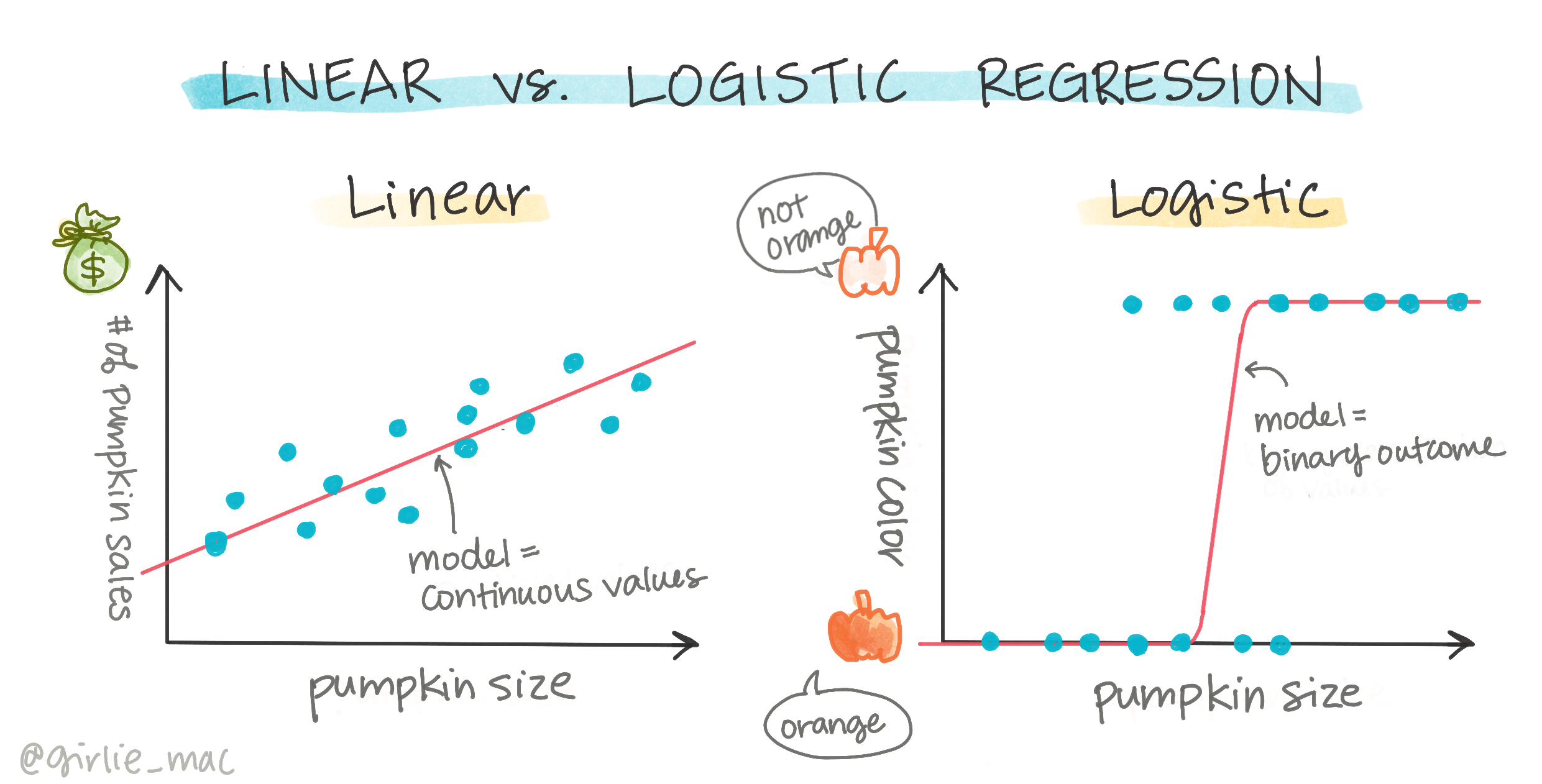
La regressione logistica differisce dalla regressione lineare, che hai imparato in precedenza, in alcuni modi importanti.

🎥 Clicca sull'immagine sopra per una breve panoramica sulla regressione logistica.

Classificazione binaria

La regressione logistica non offre le stesse funzionalità della regressione lineare. La prima offre una previsione su una categoria binaria ("bianca o non bianca"), mentre la seconda è in grado di prevedere valori continui, ad esempio, dato l'origine di una zucca e il momento del raccolto, quanto aumenterà il suo prezzo.

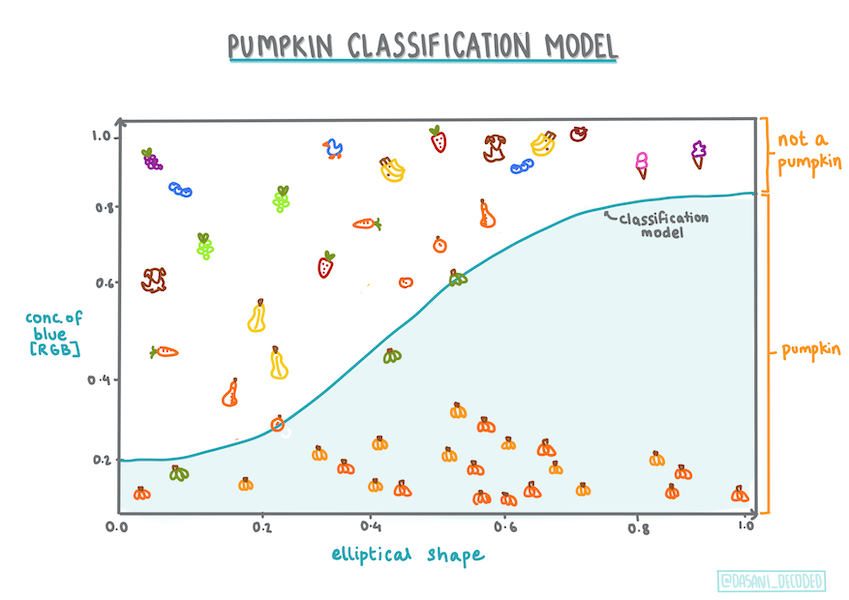
Infografica di Dasani Madipalli

Altre classificazioni

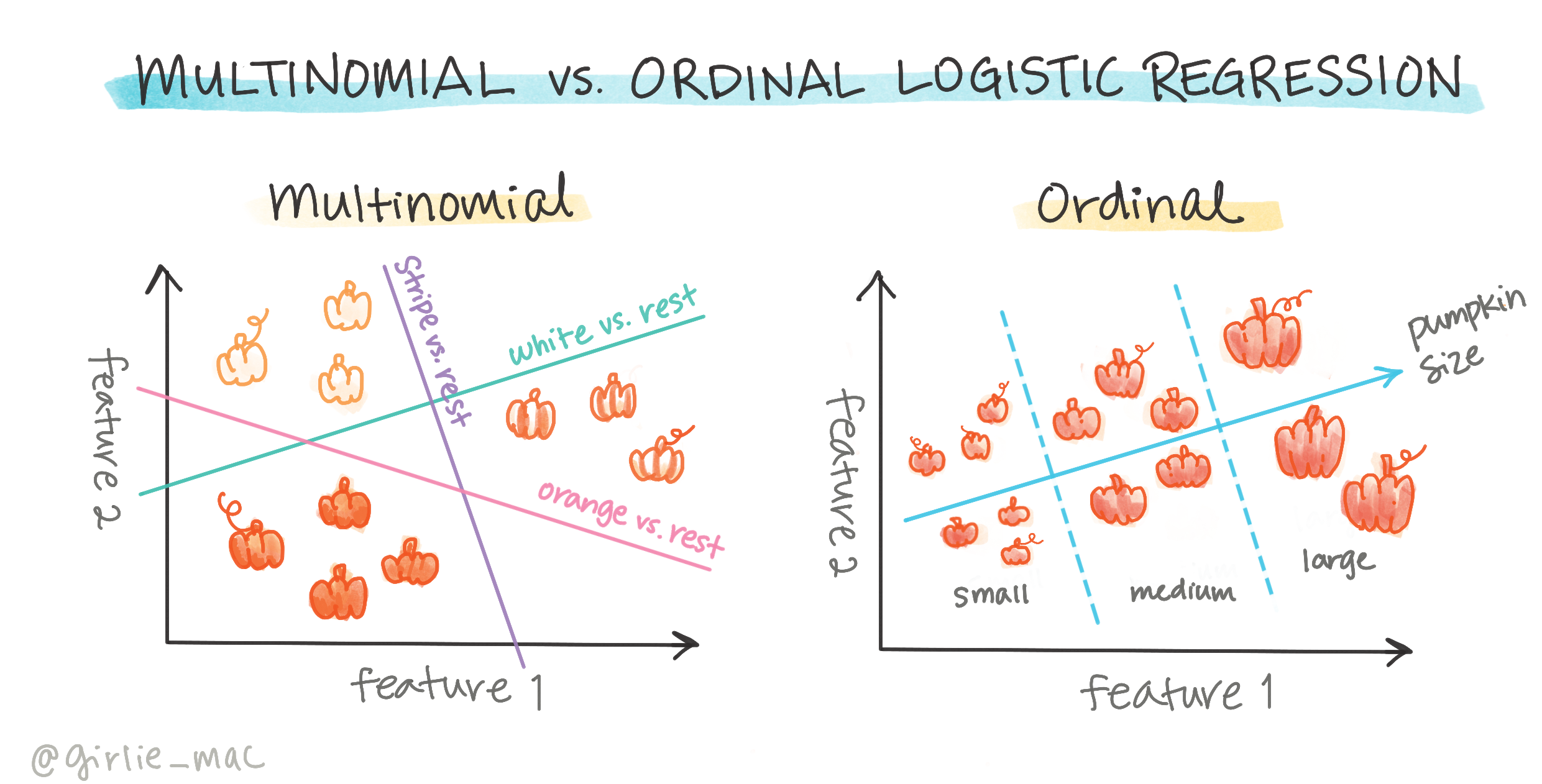
Esistono altri tipi di regressione logistica, tra cui multinomiale e ordinale:

Multinomiale, che coinvolge più di una categoria - "Arancione, Bianca e a Strisce".
Ordinale, che coinvolge categorie ordinate, utile se volessimo ordinare i nostri risultati in modo logico, come le zucche ordinate per un numero finito di dimensioni (mini, sm, med, lg, xl, xxl).

Le variabili NON devono essere correlate

Ricordi come la regressione lineare funzionava meglio con variabili più correlate? La regressione logistica è l'opposto: le variabili non devono essere allineate. Questo funziona per i dati che hanno correlazioni piuttosto deboli.

Hai bisogno di molti dati puliti

La regressione logistica fornirà risultati più accurati se utilizzi più dati; il nostro piccolo dataset non è ottimale per questo compito, quindi tienilo a mente.

🎥 Clicca sull'immagine sopra per una breve panoramica sulla preparazione dei dati per la regressione lineare.

✅ Pensa ai tipi di dati che si prestano bene alla regressione logistica.

Esercizio - pulire i dati

Per prima cosa, pulisci un po' i dati, eliminando i valori nulli e selezionando solo alcune colonne:

Aggiungi il seguente codice:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Puoi sempre dare un'occhiata al tuo nuovo dataframe:

pumpkins.info

Visualizzazione - grafico categoriale

A questo punto hai caricato il notebook iniziale con i dati delle zucche e li hai puliti per preservare un dataset contenente alcune variabili, inclusa Color. Visualizziamo il dataframe nel notebook utilizzando una libreria diversa: Seaborn, che è costruita su Matplotlib che abbiamo usato in precedenza.

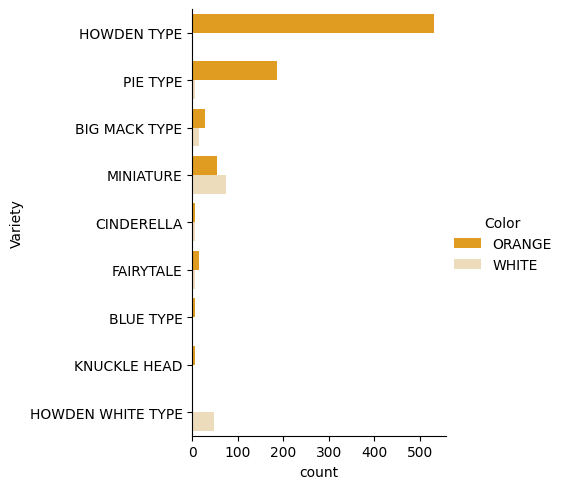
Seaborn offre modi interessanti per visualizzare i tuoi dati. Ad esempio, puoi confrontare le distribuzioni dei dati per ogni Variety e Color in un grafico categoriale.

Crea un grafico di questo tipo utilizzando la funzione catplot, usando i dati delle zucche pumpkins e specificando una mappatura di colori per ogni categoria di zucca (arancione o bianca):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Osservando i dati, puoi vedere come i dati di Color si relazionano a Variety.

✅ Dato questo grafico categoriale, quali esplorazioni interessanti puoi immaginare?

Pre-elaborazione dei dati: codifica delle caratteristiche e delle etichette

Il nostro dataset delle zucche contiene valori stringa per tutte le sue colonne. Lavorare con dati categoriali è intuitivo per gli esseri umani, ma non per le macchine. Gli algoritmi di machine learning funzionano bene con i numeri. Ecco perché la codifica è un passaggio molto importante nella fase di pre-elaborazione dei dati, poiché ci consente di trasformare i dati categoriali in dati numerici, senza perdere alcuna informazione. Una buona codifica porta alla costruzione di un buon modello.

Per la codifica delle caratteristiche ci sono due tipi principali di encoder:

Encoder ordinale: è adatto per variabili ordinali, che sono variabili categoriali i cui dati seguono un ordine logico, come la colonna Item Size nel nostro dataset. Crea una mappatura in modo che ogni categoria sia rappresentata da un numero, che è l'ordine della categoria nella colonna.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Encoder categoriale: è adatto per variabili nominali, che sono variabili categoriali i cui dati non seguono un ordine logico, come tutte le caratteristiche diverse da Item Size nel nostro dataset. È una codifica one-hot, il che significa che ogni categoria è rappresentata da una colonna binaria: la variabile codificata è uguale a 1 se la zucca appartiene a quella Variety e 0 altrimenti.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Successivamente, ColumnTransformer viene utilizzato per combinare più encoder in un unico passaggio e applicarli alle colonne appropriate.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

D'altra parte, per codificare l'etichetta, utilizziamo la classe LabelEncoder di scikit-learn, che è una classe di utilità per normalizzare le etichette in modo che contengano solo valori tra 0 e n_classes-1 (qui, 0 e 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Una volta che abbiamo codificato le caratteristiche e l'etichetta, possiamo unirle in un nuovo dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Quali sono i vantaggi di utilizzare un encoder ordinale per la colonna Item Size?

Analizzare le relazioni tra variabili

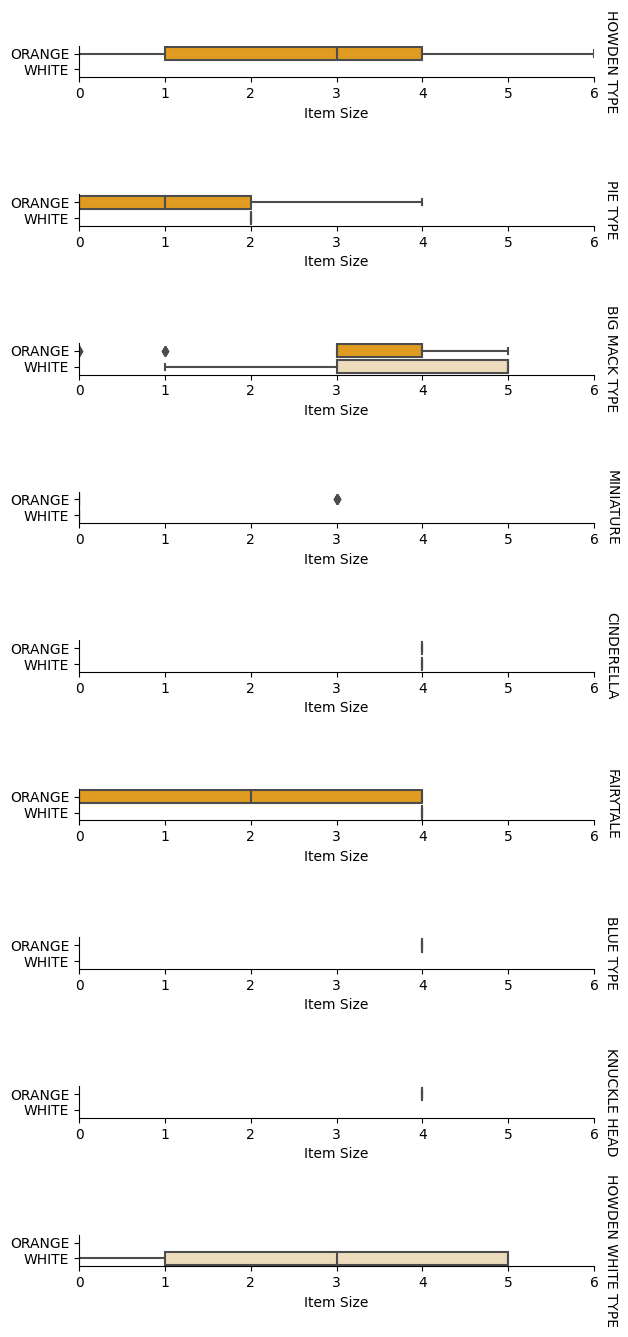
Ora che abbiamo pre-elaborato i nostri dati, possiamo analizzare le relazioni tra le caratteristiche e l'etichetta per avere un'idea di quanto bene il modello sarà in grado di prevedere l'etichetta date le caratteristiche. Il modo migliore per eseguire questo tipo di analisi è rappresentare i dati graficamente. Utilizzeremo nuovamente la funzione catplot di Seaborn per visualizzare le relazioni tra Item Size, Variety e Color in un grafico categoriale. Per rappresentare meglio i dati utilizzeremo la colonna codificata Item Size e la colonna non codificata Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Utilizzare un grafico swarm

Poiché Color è una categoria binaria (Bianca o Non Bianca), necessita di 'un approccio specializzato per la visualizzazione'. Esistono altri modi per visualizzare la relazione di questa categoria con altre variabili.

Puoi visualizzare le variabili fianco a fianco con i grafici di Seaborn.

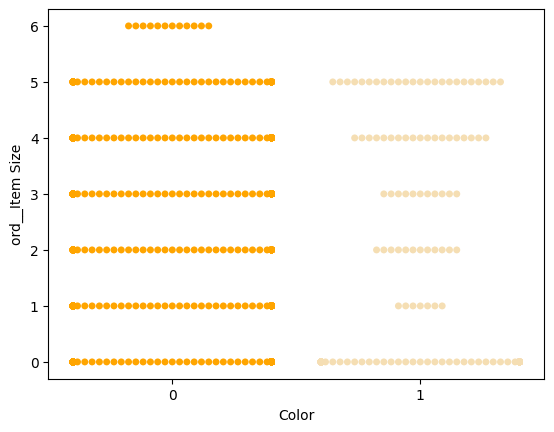
Prova un grafico 'swarm' per mostrare la distribuzione dei valori:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Attenzione: il codice sopra potrebbe generare un avviso, poiché Seaborn non riesce a rappresentare una quantità così elevata di punti dati in un grafico swarm. Una possibile soluzione è ridurre la dimensione del marker, utilizzando il parametro 'size'. Tuttavia, tieni presente che ciò influisce sulla leggibilità del grafico.

🧮 Mostrami la matematica

La regressione logistica si basa sul concetto di 'massima verosimiglianza' utilizzando funzioni sigmoid. Una 'Funzione Sigmoid' su un grafico ha una forma a 'S'. Prende un valore e lo mappa tra 0 e 1. La sua curva è anche chiamata 'curva logistica'. La sua formula è la seguente:

dove il punto medio della sigmoid si trova al punto 0 di x, L è il valore massimo della curva e k è la pendenza della curva. Se il risultato della funzione è maggiore di 0.5, l'etichetta in questione verrà assegnata alla classe '1' della scelta binaria. In caso contrario, verrà classificata come '0'.

Costruisci il tuo modello

Costruire un modello per trovare queste classificazioni binarie è sorprendentemente semplice in Scikit-learn.

🎥 Clicca sull'immagine sopra per una breve panoramica sulla costruzione di un modello di regressione lineare.

Seleziona le variabili che vuoi utilizzare nel tuo modello di classificazione e dividi i set di addestramento e test chiamando train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Ora puoi addestrare il tuo modello, chiamando fit() con i tuoi dati di addestramento, e stampare il risultato:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Dai un'occhiata al punteggio del tuo modello. Non è male, considerando che hai solo circa 1000 righe di dati:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Migliore comprensione tramite una matrice di confusione

Mentre puoi ottenere un rapporto sul punteggio termini stampando gli elementi sopra, potresti essere in grado di comprendere meglio il tuo modello utilizzando una matrice di confusione per aiutarci a capire come il modello sta funzionando.

🎓 Una 'matrice di confusione' (o 'matrice di errore') è una tabella che esprime i veri vs. falsi positivi e negativi del tuo modello, valutando così l'accuratezza delle previsioni.

Per utilizzare una matrice di confusione, chiama confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Dai un'occhiata alla matrice di confusione del tuo modello:

array([[162,   4],
       [ 11,  22]])

In Scikit-learn, le righe (asse 0) sono le etichette reali e le colonne (asse 1) sono le etichette previste.

	0	1
0	TN	FP
1	FN	TP

Cosa sta succedendo qui? Supponiamo che il nostro modello sia chiamato a classificare le zucche tra due categorie binarie, categoria 'bianca' e categoria 'non-bianca'.

Se il tuo modello prevede una zucca come non bianca e appartiene alla categoria 'non-bianca' nella realtà, la chiamiamo vero negativo, mostrato dal numero in alto a sinistra.
Se il tuo modello prevede una zucca come bianca e appartiene alla categoria 'non-bianca' nella realtà, la chiamiamo falso negativo, mostrato dal numero in basso a sinistra.
Se il tuo modello prevede una zucca come non bianca e appartiene alla categoria 'bianca' nella realtà, la chiamiamo falso positivo, mostrato dal numero in alto a destra.
Se il tuo modello prevede una zucca come bianca e appartiene alla categoria 'bianca' nella realtà, la chiamiamo vero positivo, mostrato dal numero in basso a destra.

Come avrai intuito, è preferibile avere un numero maggiore di veri positivi e veri negativi e un numero minore di falsi positivi e falsi negativi, il che implica che il modello funziona meglio. Come si relaziona la matrice di confusione con precisione e richiamo? Ricorda, il report di classificazione stampato sopra ha mostrato una precisione (0.85) e un richiamo (0.67).

Precisione = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Richiamo = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ D: Secondo la matrice di confusione, come si è comportato il modello? R: Non male; ci sono un buon numero di veri negativi ma anche alcuni falsi negativi.

Rivediamo i termini che abbiamo visto in precedenza con l'aiuto della mappatura TP/TN e FP/FN della matrice di confusione:

🎓 Precisione: TP/(TP + FP) La frazione di istanze rilevanti tra quelle recuperate (ad esempio, quali etichette sono state ben etichettate).

🎓 Richiamo: TP/(TP + FN) La frazione di istanze rilevanti che sono state recuperate, indipendentemente dal fatto che siano ben etichettate o meno.

🎓 f1-score: (2 * precisione * richiamo)/(precisione + richiamo) Una media ponderata di precisione e richiamo, con il migliore pari a 1 e il peggiore pari a 0.

🎓 Supporto: Il numero di occorrenze di ciascuna etichetta recuperata.

🎓 Accuratezza: (TP + TN)/(TP + TN + FP + FN) La percentuale di etichette previste correttamente per un campione.

🎓 Media Macro: Il calcolo della media non ponderata delle metriche per ciascuna etichetta, senza tenere conto dello squilibrio delle etichette.

🎓 Media Ponderata: Il calcolo della media delle metriche per ciascuna etichetta, tenendo conto dello squilibrio delle etichette ponderandole in base al loro supporto (il numero di istanze vere per ciascuna etichetta).

✅ Riesci a pensare a quale metrica dovresti prestare attenzione se vuoi che il tuo modello riduca il numero di falsi negativi?

Visualizzare la curva ROC di questo modello

🎥 Clicca sull'immagine sopra per una breve panoramica delle curve ROC

Facciamo un'altra visualizzazione per vedere la cosiddetta curva 'ROC':

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

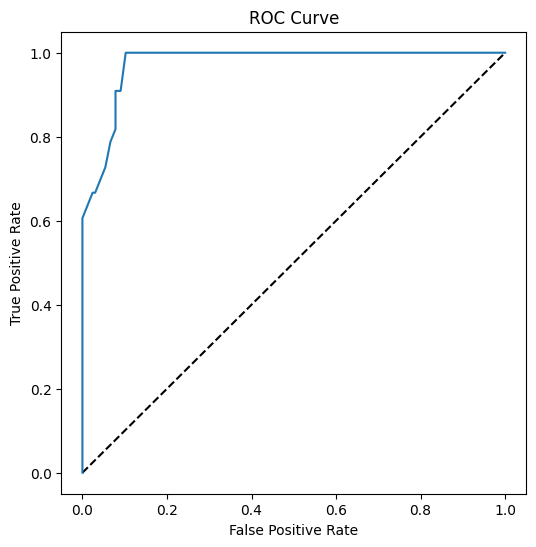
Usando Matplotlib, traccia la Curva Caratteristica Operativa del Ricevitore o ROC del modello. Le curve ROC sono spesso utilizzate per ottenere una visione dell'output di un classificatore in termini di veri positivi rispetto ai falsi positivi. "Le curve ROC presentano tipicamente il tasso di veri positivi sull'asse Y e il tasso di falsi positivi sull'asse X." Pertanto, la ripidità della curva e lo spazio tra la linea mediana e la curva sono importanti: si desidera una curva che si diriga rapidamente verso l'alto e oltre la linea. Nel nostro caso, ci sono falsi positivi iniziali, e poi la linea si dirige correttamente verso l'alto e oltre:

Infine, utilizza l'API roc_auc_score di Scikit-learn per calcolare l'effettiva 'Area Sotto la Curva' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Il risultato è 0.9749908725812341. Dato che l'AUC varia da 0 a 1, si desidera un punteggio elevato, poiché un modello che è corretto al 100% nelle sue previsioni avrà un AUC di 1; in questo caso, il modello è abbastanza buono.

Nelle lezioni future sulle classificazioni, imparerai come iterare per migliorare i punteggi del tuo modello. Ma per ora, congratulazioni! Hai completato queste lezioni sulla regressione!

🚀Sfida

C'è molto altro da esplorare riguardo alla regressione logistica! Ma il modo migliore per imparare è sperimentare. Trova un dataset che si presti a questo tipo di analisi e costruisci un modello con esso. Cosa impari? suggerimento: prova Kaggle per dataset interessanti.

Quiz post-lezione

Revisione e Studio Autonomo

Leggi le prime pagine di questo documento di Stanford su alcuni usi pratici della regressione logistica. Pensa ai compiti che sono più adatti per uno o l'altro tipo di compiti di regressione che abbiamo studiato fino a questo punto. Cosa funzionerebbe meglio?

Compito

Riprova questa regressione

Disclaimer:
Questo documento è stato tradotto utilizzando il servizio di traduzione automatica Co-op Translator. Sebbene ci impegniamo per garantire l'accuratezza, si prega di notare che le traduzioni automatiche possono contenere errori o imprecisioni. Il documento originale nella sua lingua nativa dovrebbe essere considerato la fonte autorevole. Per informazioni critiche, si raccomanda una traduzione professionale effettuata da un traduttore umano. Non siamo responsabili per eventuali incomprensioni o interpretazioni errate derivanti dall'uso di questa traduzione.

23 KiB Raw Permalink Blame History