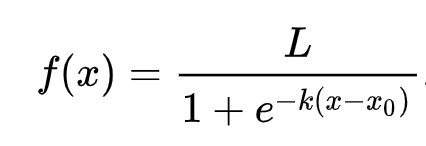22 KiB

Raw Permalink Blame History

Logistička regresija za predviđanje kategorija

Kviz prije predavanja

Ova lekcija je dostupna i na R jeziku!

Uvod

U ovoj završnoj lekciji o regresiji, jednoj od osnovnih klasičnih tehnika strojnog učenja, proučit ćemo logističku regresiju. Ovu tehniku koristite za otkrivanje obrazaca kako biste predvidjeli binarne kategorije. Je li ovaj slatkiš čokolada ili nije? Je li ova bolest zarazna ili nije? Hoće li ovaj kupac odabrati ovaj proizvod ili neće?

U ovoj lekciji naučit ćete:

Novi alat za vizualizaciju podataka
Tehnike logističke regresije

✅ Produbite svoje razumijevanje rada s ovom vrstom regresije u ovom modulu za učenje

Preduvjeti

Radili smo s podacima o bundevama i sada smo dovoljno upoznati s njima da shvatimo kako postoji jedna binarna kategorija s kojom možemo raditi: Boja.

Izgradimo model logističke regresije kako bismo predvidjeli, na temelju nekih varijabli, koje je boje određena bundeva (narančasta 🎃 ili bijela 👻).

Zašto govorimo o binarnoj klasifikaciji u lekciji o regresiji? Samo radi jezične praktičnosti, jer je logistička regresija zapravo metoda klasifikacije, iako se temelji na linearnim modelima. Saznajte više o drugim načinima klasifikacije podataka u sljedećoj grupi lekcija.

Definirajte pitanje

Za naše potrebe, izrazit ćemo ovo kao binarnu kategoriju: 'Bijela' ili 'Nije bijela'. U našem skupu podataka postoji i kategorija 'prugasta', ali ima malo primjera te kategorije, pa je nećemo koristiti. Ionako nestaje kada uklonimo null vrijednosti iz skupa podataka.

🎃 Zanimljivost: bijele bundeve ponekad nazivamo 'duh' bundevama. Nisu baš jednostavne za rezbarenje, pa nisu toliko popularne kao narančaste, ali izgledaju zanimljivo! Tako bismo svoje pitanje mogli preformulirati i kao: 'Duh' ili 'Nije duh'. 👻

O logističkoj regresiji

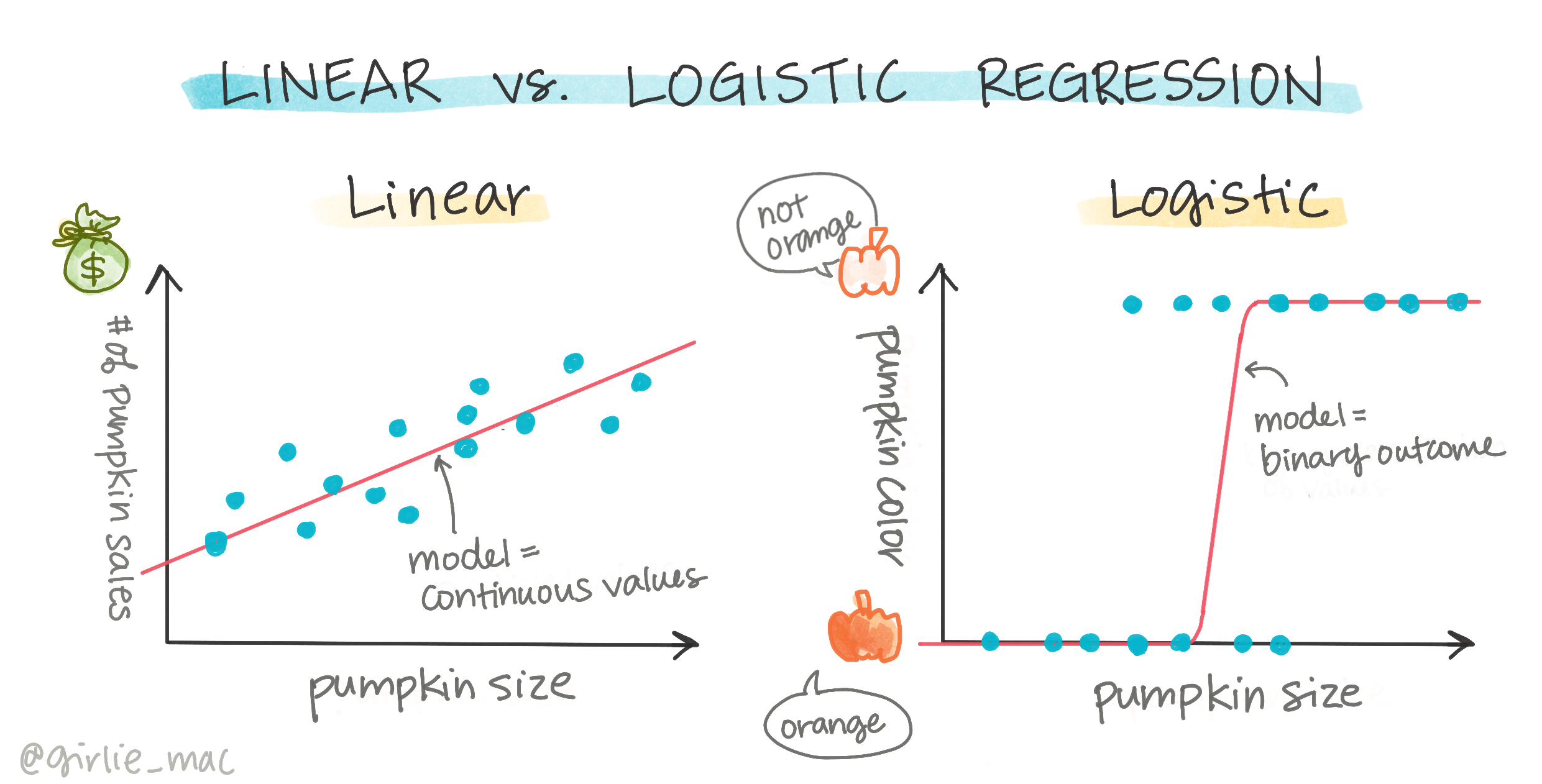
Logistička regresija razlikuje se od linearne regresije, o kojoj ste ranije učili, u nekoliko važnih aspekata.

🎥 Kliknite na sliku iznad za kratki video pregled logističke regresije.

Binarna klasifikacija

Logistička regresija ne nudi iste mogućnosti kao linearna regresija. Prva nudi predviđanje binarne kategorije ("bijela ili nije bijela"), dok druga može predvidjeti kontinuirane vrijednosti, na primjer, s obzirom na podrijetlo bundeve i vrijeme berbe, koliko će joj cijena porasti.

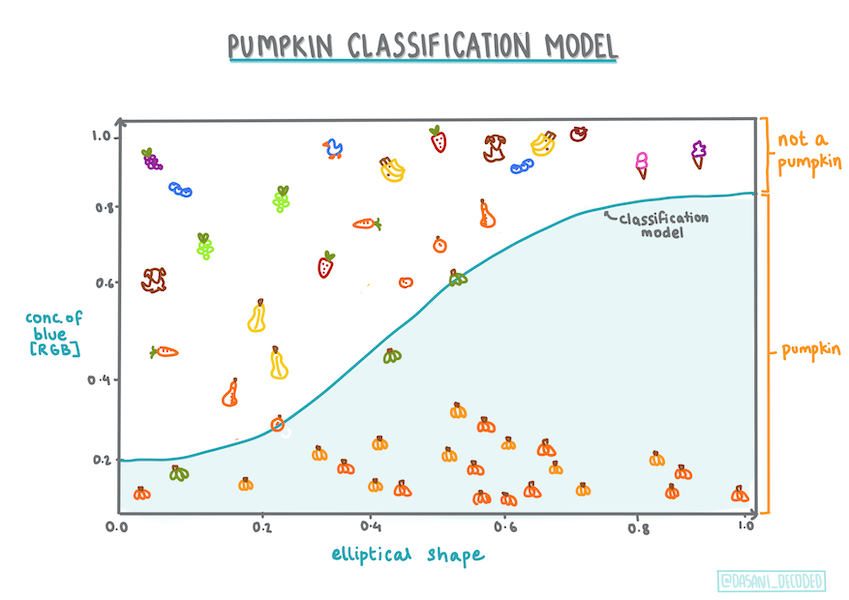
Infografika: Dasani Madipalli

Druge vrste klasifikacije

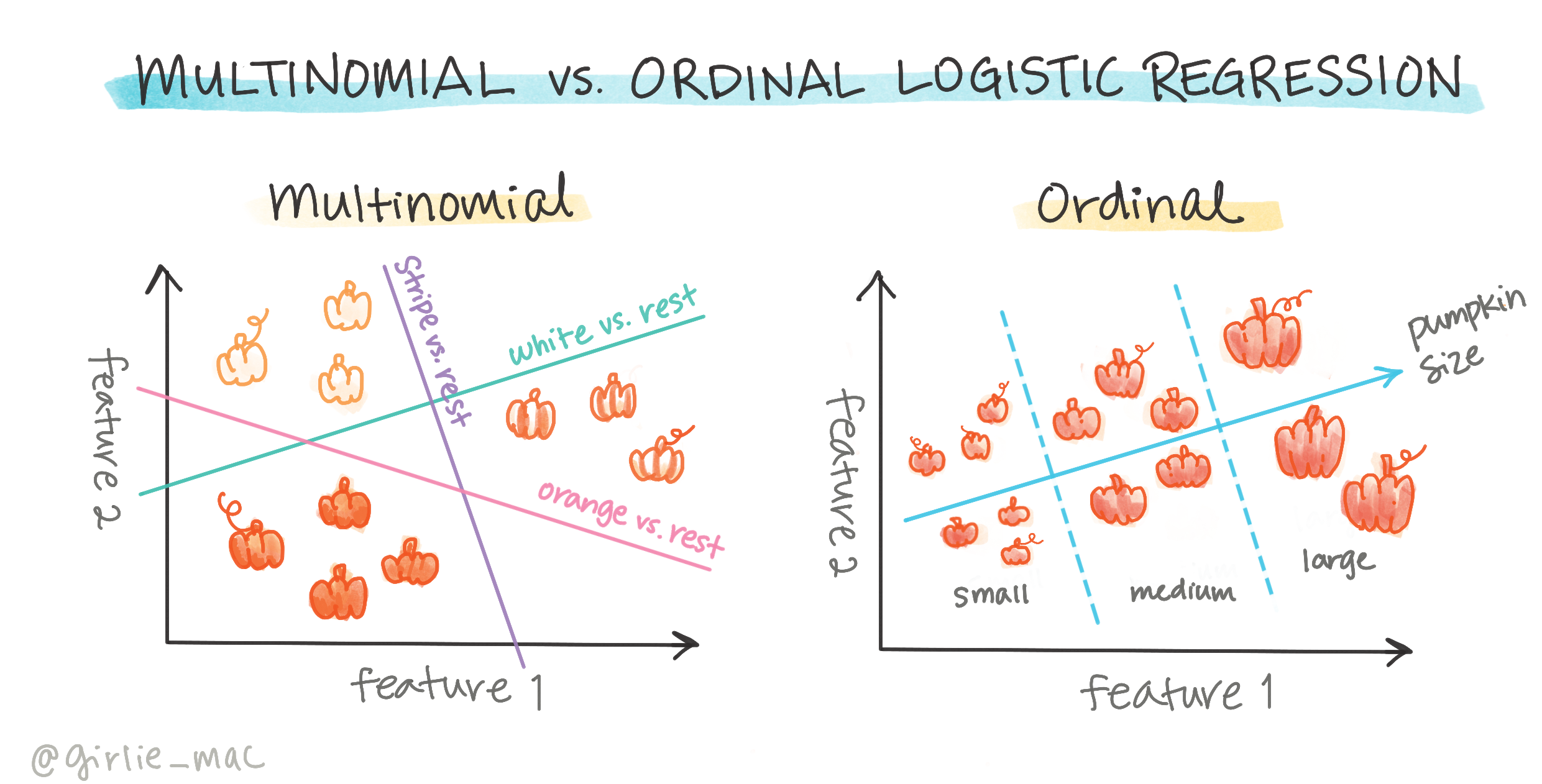
Postoje i druge vrste logističke regresije, uključujući multinomijalnu i ordinalnu:

Multinomijalna, koja uključuje više od jedne kategorije - "Narančasta, Bijela i Prugasta".
Ordinalna, koja uključuje uređene kategorije, korisno ako želimo logički poredati ishode, poput bundeva koje su poredane prema veličini (mini, sm, med, lg, xl, xxl).

Varijable NE moraju biti povezane

Sjećate se kako je linearna regresija bolje funkcionirala s više povezanih varijabli? Logistička regresija je suprotna - varijable ne moraju biti povezane. To odgovara ovim podacima koji imaju prilično slabe korelacije.

Potrebno je puno čistih podataka

Logistička regresija daje točnije rezultate ako koristite više podataka; naš mali skup podataka nije optimalan za ovaj zadatak, pa to imajte na umu.

✅ Razmislite o vrstama podataka koje bi bile prikladne za logističku regresiju.

Vježba - priprema podataka

Prvo, očistite podatke, uklonite null vrijednosti i odaberite samo neke stupce:

Dodajte sljedeći kod:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Uvijek možete zaviriti u svoj novi dataframe:

pumpkins.info

Vizualizacija - kategorijalni graf

Do sada ste ponovno učitali početnu bilježnicu s podacima o bundevama i očistili je kako biste sačuvali skup podataka koji sadrži nekoliko varijabli, uključujući Boju. Vizualizirajmo dataframe u bilježnici koristeći drugu biblioteku: Seaborn, koja je izgrađena na Matplotlibu koji smo ranije koristili.

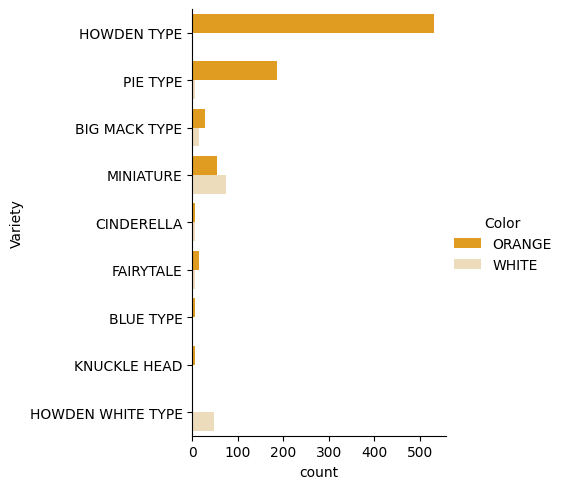
Seaborn nudi zanimljive načine za vizualizaciju podataka. Na primjer, možete usporediti distribucije podataka za svaku Varijantu i Boju u kategorijalnom grafu.

Stvorite takav graf koristeći funkciju catplot, koristeći naše podatke o bundevama pumpkins i specificirajući mapiranje boja za svaku kategoriju bundeva (narančasta ili bijela):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Promatrajući podatke, možete vidjeti kako se podaci o boji odnose na varijantu.

✅ Na temelju ovog kategorijalnog grafa, koje zanimljive analize možete zamisliti?

Predobrada podataka: kodiranje značajki i oznaka

Naš skup podataka o bundevama sadrži tekstualne vrijednosti za sve stupce. Rad s kategorijalnim podacima intuitivan je za ljude, ali ne i za strojeve. Algoritmi strojnog učenja bolje rade s brojevima. Zato je kodiranje vrlo važan korak u fazi predobrade podataka jer nam omogućuje pretvaranje kategorijalnih podataka u numeričke, bez gubitka informacija. Dobro kodiranje vodi do izgradnje dobrog modela.

Za kodiranje značajki postoje dvije glavne vrste kodera:

Ordinalni koder: dobro odgovara za ordinalne varijable, koje su kategorijalne varijable čiji podaci slijede logički redoslijed, poput stupca Veličina predmeta u našem skupu podataka. Stvara mapiranje tako da je svaka kategorija predstavljena brojem, koji odgovara redoslijedu kategorije u stupcu.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorijalni koder: dobro odgovara za nominalne varijable, koje su kategorijalne varijable čiji podaci ne slijede logički redoslijed, poput svih značajki osim Veličine predmeta u našem skupu podataka. To je kodiranje s jednom vrućom vrijednošću, što znači da je svaka kategorija predstavljena binarnim stupcem: kodirana varijabla jednaka je 1 ako bundeva pripada toj varijanti, a 0 inače.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Zatim se ColumnTransformer koristi za kombiniranje više kodera u jedan korak i njihovu primjenu na odgovarajuće stupce.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

S druge strane, za kodiranje oznaka koristimo klasu LabelEncoder iz scikit-learn biblioteke, koja je pomoćna klasa za normalizaciju oznaka tako da sadrže samo vrijednosti između 0 i n_klasa-1 (ovdje, 0 i 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Nakon što smo kodirali značajke i oznake, možemo ih spojiti u novi dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Koje su prednosti korištenja ordinalnog kodera za stupac Veličina predmeta?

Analiza odnosa između varijabli

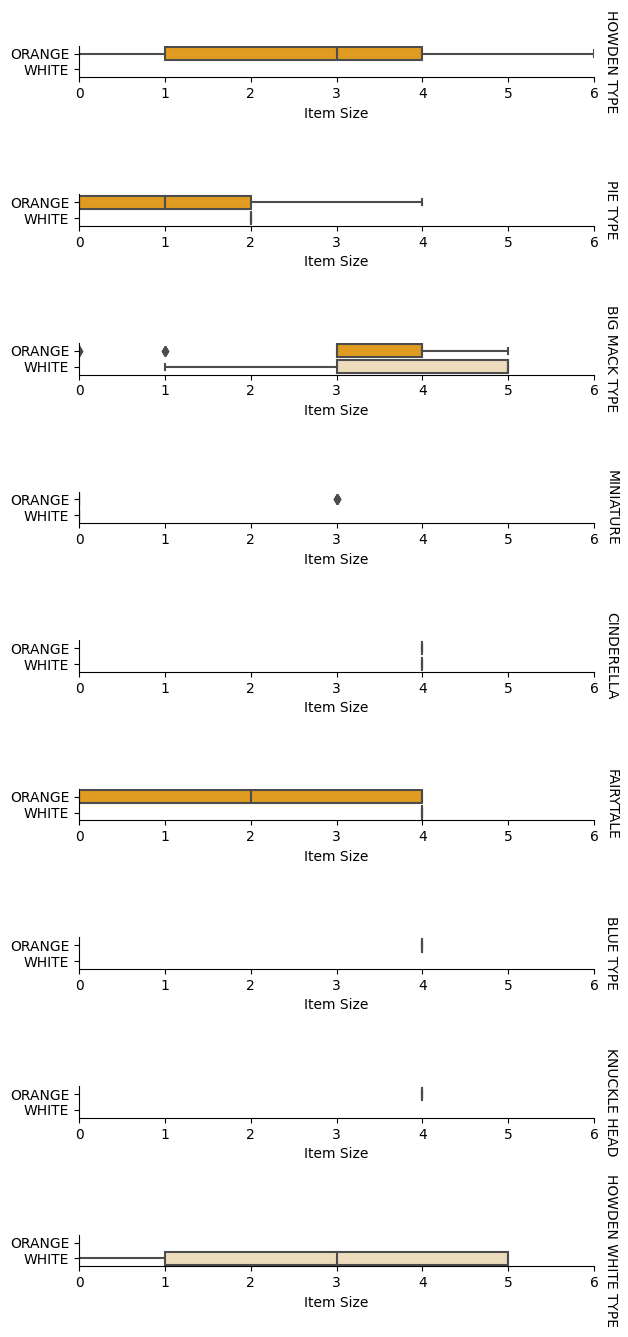
Sada kada smo obradili podatke, možemo analizirati odnose između značajki i oznaka kako bismo stekli ideju o tome koliko će model biti uspješan u predviđanju oznaka na temelju značajki. Najbolji način za izvođenje ove vrste analize je grafičko prikazivanje podataka. Ponovno ćemo koristiti funkciju catplot iz Seaborna za vizualizaciju odnosa između Veličine predmeta, Varijante i Boje u kategorijalnom grafu. Za bolje prikazivanje podataka koristit ćemo kodirani stupac Veličina predmeta i nekodirani stupac Varijanta.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

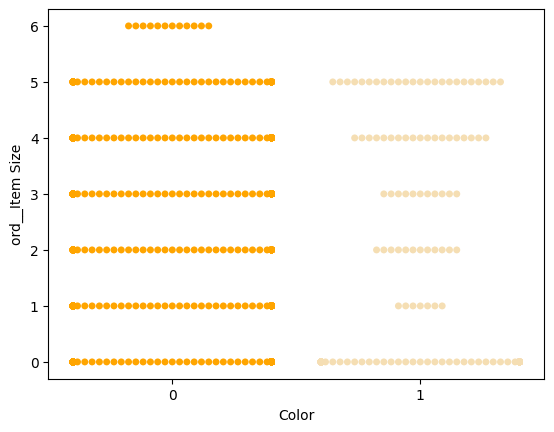
Korištenje swarm grafa

Budući da je Boja binarna kategorija (Bijela ili Nije), potrebna je 'posebna metoda za vizualizaciju'. Postoje i drugi načini za vizualizaciju odnosa ove kategorije s drugim varijablama.

Možete vizualizirati varijable usporedno pomoću Seaborn grafova.

Isprobajte 'swarm' graf za prikaz distribucije vrijednosti:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Napomena: kod iznad može generirati upozorenje jer Seaborn ne može prikazati toliku količinu podataka u swarm grafu. Moguće rješenje je smanjenje veličine markera pomoću parametra 'size'. Međutim, imajte na umu da to može utjecati na čitljivost grafa.

🧮 Matematika iza toga

Logistička regresija temelji se na konceptu 'maksimalne vjerodostojnosti' koristeći sigmoidne funkcije. 'Sigmoidna funkcija' na grafu izgleda poput oblika slova 'S'. Uzima vrijednost i mapira je na raspon između 0 i 1. Njezina krivulja također se naziva 'logistička krivulja'. Formula izgleda ovako:

gdje se sredina sigmoidne funkcije nalazi na x-ovoj 0 točki, L je maksimalna vrijednost krivulje, a k je strmina krivulje. Ako je ishod funkcije veći od 0.5, oznaka će biti dodijeljena klasi '1' binarnog izbora. Ako nije, bit će klasificirana kao '0'.

Izgradite svoj model

Izgradnja modela za pronalaženje binarne klasifikacije iznenađujuće je jednostavna u Scikit-learn biblioteci.

🎥 Kliknite na sliku iznad za kratki video pregled izgradnje modela logističke regresije.

Odaberite varijable koje želite koristiti u svom modelu klasifikacije i podijelite skup podataka na trening i testni pozivom train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Sada možete trenirati svoj model pozivom fit() s vašim trening podacima i ispisati njegov rezultat:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Pogledajte rezultat svog modela. Nije loše, s obzirom na to da imate samo oko 1000 redaka podataka:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Bolje razumijevanje putem matrice konfuzije

Iako možete dobiti izvještaj o rezultatima modela termini ispisivanjem gore navedenih stavki, možda ćete bolje razumjeti svoj model korištenjem matrice konfuzije koja pomaže razumjeti kako model funkcionira.

🎓 'Matrica konfuzije' (ili 'matrica pogrešaka') je tablica koja izražava stvarne i lažne pozitivne i negativne rezultate vašeg modela, čime se procjenjuje točnost predviđanja.

Za korištenje matrice konfuzije, pozovite confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Pogledajte matricu konfuzije svog modela:

array([[162,   4],
       [ 11,  22]])

U Scikit-learn biblioteci, redovi (os x) predstavljaju stvarne oznake, a stupci (os y) predviđene oznake.

	0	1
0	TN	FP
1	FN	TP

Što se ovdje događa? Recimo da naš model treba klasificirati bundeve između dvije binarne kategorije, kategorije 'bijela' i kategorije 'nije bijela'.

Ako vaš model predvidi bundevu kao 'nije bijela', a ona stvarno pripada kategoriji 'nije bijela', to nazivamo pravim negativnim rezultatom, prikazanim u gornjem lijevom kutu.
Ako vaš model predvidi bundevu kao 'bijela', a ona stvarno pripada kategoriji 'nije bijela', to nazivamo lažnim negativnim rezultatom, prikazanim u donjem lijevom kutu.
Ako vaš model predvidi bundevu kao 'nije bijela', a ona stvarno pripada kategoriji 'bijela', to nazivamo lažnim pozitivnim rezultatom, prikazanim u gornjem desnom kutu.
Ako vaš model predvidi bundevu kao 'bijela', a ona stvarno pripada kategoriji 'bijela', to nazivamo pravim pozitivnim rezultatom, prikazanim u donjem desnom kutu.

Kao što ste mogli pretpostaviti, poželjno je imati veći broj pravih pozitivnih i pravih negativnih rezultata te manji broj lažnih pozitivnih i lažnih negativnih rezultata, što implicira da model bolje funkcionira. Kako se matrica zabune odnosi na preciznost i odziv? Zapamtite, izvještaj o klasifikaciji prikazan iznad pokazao je preciznost (0.85) i odziv (0.67).

Preciznost = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Odziv = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ P: Prema matrici zabune, kako je model prošao? O: Nije loše; postoji dobar broj točnih negativnih, ali i nekoliko lažnih negativnih.

Ponovno ćemo pogledati pojmove koje smo ranije vidjeli uz pomoć mapiranja TP/TN i FP/FN u matrici zabune:

🎓 Preciznost: TP/(TP + FP) Omjer relevantnih instanci među pronađenim instancama (npr. koje oznake su dobro označene).

🎓 Odziv: TP/(TP + FN) Omjer relevantnih instanci koje su pronađene, bez obzira jesu li dobro označene ili ne.

🎓 f1-score: (2 * preciznost * odziv)/(preciznost + odziv) Ponderirani prosjek preciznosti i odziva, gdje je najbolji rezultat 1, a najgori 0.

🎓 Podrška: Broj pojavljivanja svake pronađene oznake.

🎓 Točnost: (TP + TN)/(TP + TN + FP + FN) Postotak oznaka koje su točno predviđene za uzorak.

🎓 Makro prosjek: Izračunavanje neponderiranog srednjeg rezultata za svaku oznaku, ne uzimajući u obzir neravnotežu oznaka.

🎓 Ponderirani prosjek: Izračunavanje srednjeg rezultata za svaku oznaku, uzimajući u obzir neravnotežu oznaka ponderiranjem prema njihovoj podršci (broj točnih instanci za svaku oznaku).

✅ Možete li zamisliti koji bi metrik trebali pratiti ako želite da vaš model smanji broj lažnih negativnih?

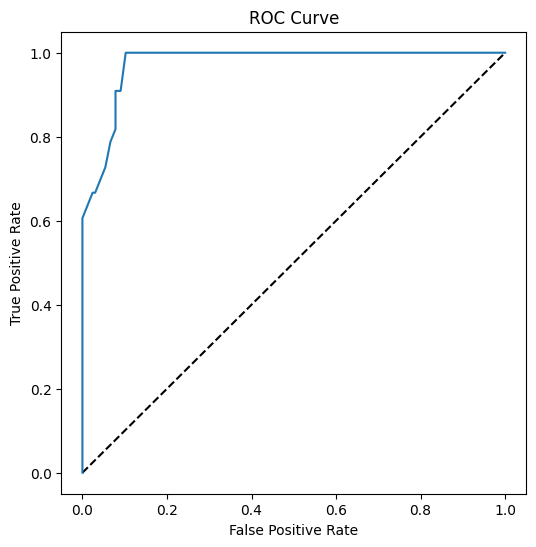
Vizualizirajte ROC krivulju ovog modela

🎥 Kliknite na sliku iznad za kratki video pregled ROC krivulja.

Napravimo još jednu vizualizaciju kako bismo vidjeli takozvanu 'ROC' krivulju:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Koristeći Matplotlib, nacrtajte Receiving Operating Characteristic ili ROC krivulju modela. ROC krivulje se često koriste za pregled izlaza klasifikatora u smislu njegovih točnih i lažnih pozitivnih. "ROC krivulje obično prikazuju stopu točnih pozitivnih na Y osi, a stopu lažnih pozitivnih na X osi." Dakle, strmina krivulje i prostor između središnje linije i krivulje su važni: želite krivulju koja brzo ide gore i preko linije. U našem slučaju, postoje lažni pozitivni na početku, a zatim linija ide gore i preko pravilno:

Na kraju, koristite Scikit-learnov roc_auc_score API za izračun stvarne 'Površine ispod krivulje' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Rezultat je 0.9749908725812341. S obzirom na to da AUC varira od 0 do 1, želite visok rezultat, jer model koji je 100% točan u svojim predviđanjima ima AUC od 1; u ovom slučaju, model je prilično dobar.

U budućim lekcijama o klasifikacijama naučit ćete kako iterirati kako biste poboljšali rezultate svog modela. Ali za sada, čestitamo! Završili ste ove lekcije o regresiji!

🚀Izazov

Ima još puno toga za istražiti o logističkoj regresiji! No, najbolji način za učenje je eksperimentiranje. Pronađite skup podataka koji se dobro uklapa u ovu vrstu analize i izradite model s njim. Što ste naučili? savjet: pokušajte Kaggle za zanimljive skupove podataka.

Kviz nakon predavanja

Pregled i samostalno učenje

Pročitajte prvih nekoliko stranica ovog rada sa Stanforda o nekim praktičnim primjenama logističke regresije. Razmislite o zadacima koji su bolje prilagođeni jednoj ili drugoj vrsti regresijskih zadataka koje smo do sada proučavali. Što bi najbolje funkcioniralo?

Zadatak

Ponovno pokušavanje ove regresije

Odricanje od odgovornosti:
Ovaj dokument je preveden korištenjem AI usluge za prevođenje Co-op Translator. Iako nastojimo osigurati točnost, imajte na umu da automatski prijevodi mogu sadržavati pogreške ili netočnosti. Izvorni dokument na izvornom jeziku treba smatrati mjerodavnim izvorom. Za ključne informacije preporučuje se profesionalni prijevod od strane stručnjaka. Ne preuzimamo odgovornost za bilo kakve nesporazume ili pogrešne interpretacije proizašle iz korištenja ovog prijevoda.

22 KiB Raw Permalink Blame History