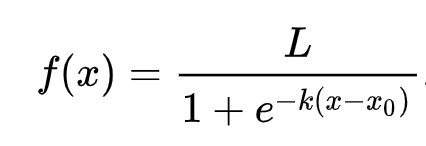26 KiB
רגרסיה לוגיסטית לחיזוי קטגוריות
מבחן מקדים להרצאה
השיעור הזה זמין גם ב-R!
מבוא
בשיעור האחרון על רגרסיה, אחת מטכניקות ה-ML הקלאסיות הבסיסיות, נבחן את הרגרסיה הלוגיסטית. תשתמשו בטכניקה זו כדי לגלות דפוסים לחיזוי קטגוריות בינאריות. האם הממתק הזה הוא שוקולד או לא? האם המחלה הזו מדבקת או לא? האם הלקוח הזה יבחר במוצר הזה או לא?
בשיעור הזה תלמדו:
- ספרייה חדשה להדמיית נתונים
- טכניקות לרגרסיה לוגיסטית
✅ העמיקו את ההבנה שלכם בעבודה עם סוג זה של רגרסיה במודול Learn
דרישות מקדימות
לאחר שעבדנו עם נתוני הדלעת, אנחנו כבר מספיק מכירים אותם כדי להבין שיש קטגוריה בינארית אחת שאפשר לעבוד איתה: Color.
בואו נבנה מודל רגרסיה לוגיסטית כדי לחזות, בהתבסס על משתנים מסוימים, איזה צבע צפוי להיות לדלעת מסוימת (כתום 🎃 או לבן 👻).
למה אנחנו מדברים על סיווג בינארי בשיעור שמקושר לרגרסיה? רק מטעמי נוחות לשונית, שכן רגרסיה לוגיסטית היא בעצם שיטת סיווג, אם כי מבוססת על ליניאריות. למדו על דרכים אחרות לסווג נתונים בקבוצת השיעורים הבאה.
הגדרת השאלה
למטרותינו, נבטא זאת כבינארי: 'לבן' או 'לא לבן'. יש גם קטגוריה 'מפוספסת' במאגר הנתונים שלנו, אבל יש מעט מקרים שלה, ולכן לא נשתמש בה. היא נעלמת בכל מקרה ברגע שמסירים ערכים חסרים מהמאגר.
🎃 עובדה מעניינת: לפעמים אנחנו קוראים לדלעות לבנות 'דלעות רפאים'. הן לא קלות לגילוף, ולכן הן פחות פופולריות מהכתומות, אבל הן נראות מגניבות! אז אפשר גם לנסח מחדש את השאלה שלנו כ: 'רפאים' או 'לא רפאים'. 👻
על רגרסיה לוגיסטית
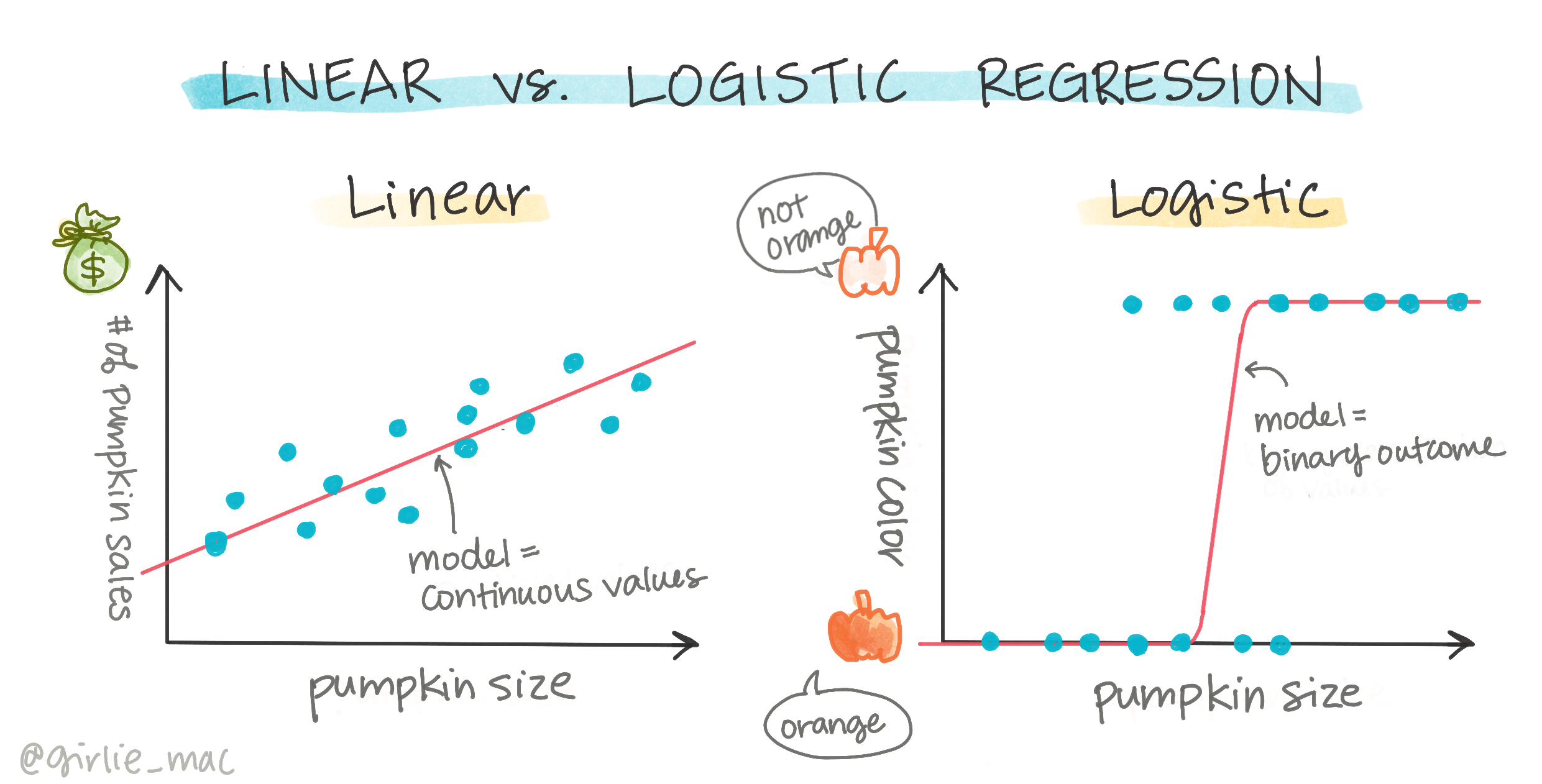
רגרסיה לוגיסטית שונה מרגרסיה ליניארית, שלמדתם עליה קודם, בכמה דרכים חשובות.
🎥 לחצו על התמונה למעלה לסרטון קצר על רגרסיה לוגיסטית.
סיווג בינארי
רגרסיה לוגיסטית לא מציעה את אותן תכונות כמו רגרסיה ליניארית. הראשונה מציעה חיזוי של קטגוריה בינארית ("לבן או לא לבן"), בעוד שהאחרונה מסוגלת לחזות ערכים רציפים, למשל בהתבסס על מקור הדלעת וזמן הקטיף, כמה המחיר שלה יעלה.
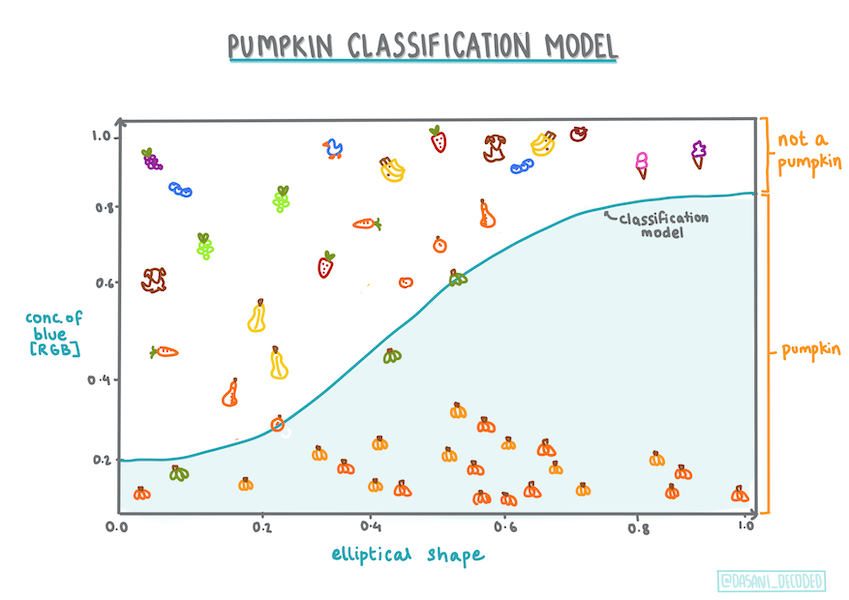
אינפוגרפיקה מאת Dasani Madipalli
סיווגים אחרים
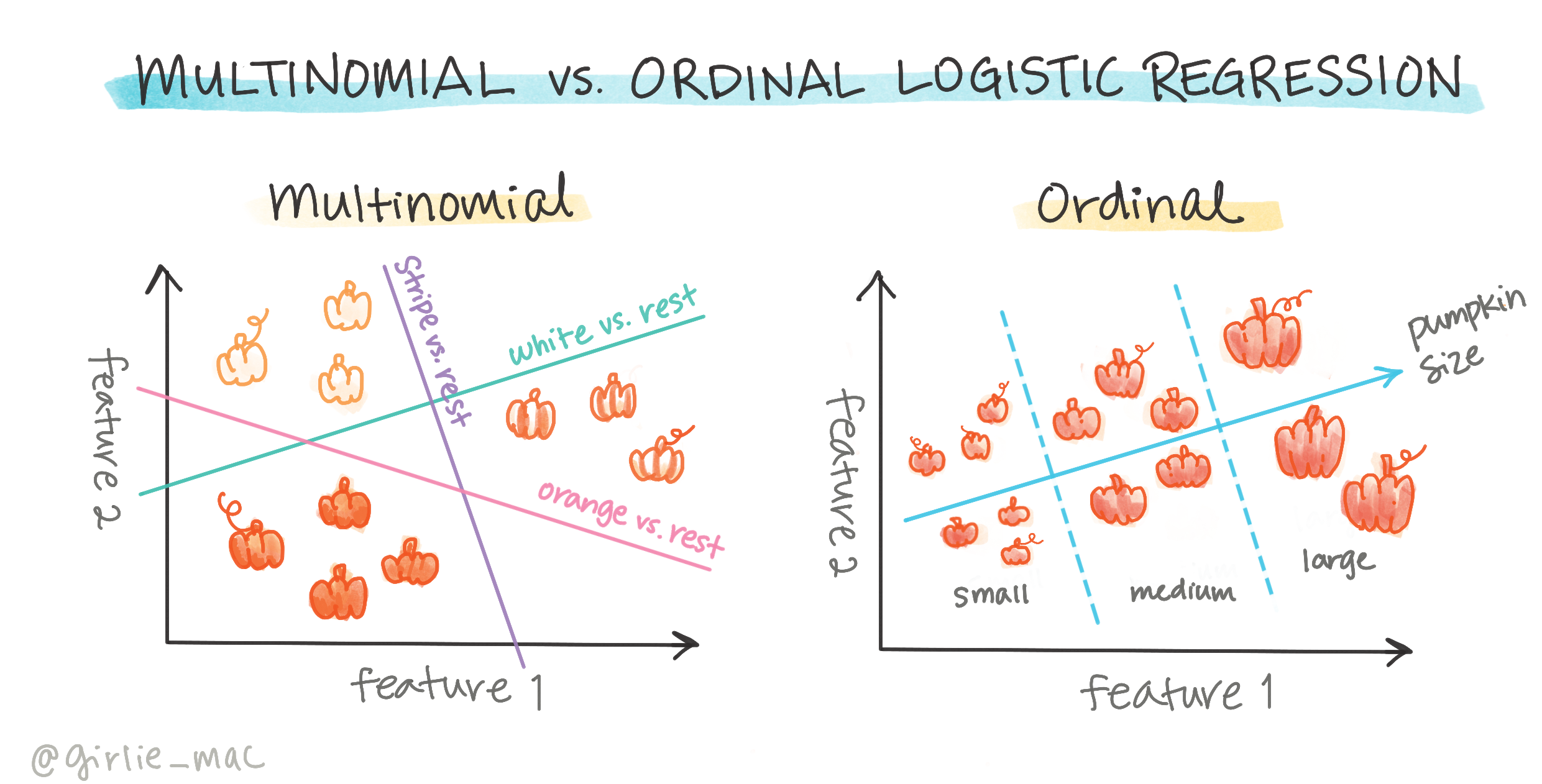
ישנם סוגים אחרים של רגרסיה לוגיסטית, כולל מולטינומיאלית ואורדינלית:
- מולטינומיאלית, שכוללת יותר מקטגוריה אחת - "כתום, לבן ומפוספס".
- אורדינלית, שכוללת קטגוריות מסודרות, שימושית אם נרצה לסדר את התוצאות שלנו באופן לוגי, כמו הדלעות שלנו שמסודרות לפי מספר סופי של גדלים (מיני, קטן, בינוני, גדול, XL, XXL).
המשתנים לא חייבים להיות מתואמים
זוכרים איך רגרסיה ליניארית עבדה טוב יותר עם משתנים מתואמים? רגרסיה לוגיסטית היא ההפך - המשתנים לא חייבים להיות מתואמים. זה עובד עבור הנתונים האלה שיש להם מתאמים חלשים יחסית.
צריך הרבה נתונים נקיים
רגרסיה לוגיסטית תיתן תוצאות מדויקות יותר אם תשתמשו ביותר נתונים; מאגר הנתונים הקטן שלנו אינו אופטימלי למשימה זו, אז קחו זאת בחשבון.
🎥 לחצו על התמונה למעלה לסרטון קצר על הכנת נתונים לרגרסיה ליניארית.
✅ חשבו על סוגי הנתונים שיתאימו לרגרסיה לוגיסטית.
תרגיל - ניקוי הנתונים
ראשית, ננקה את הנתונים מעט, נסיר ערכים חסרים ונבחר רק חלק מהעמודות:
-
הוסיפו את הקוד הבא:
columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color'] pumpkins = full_pumpkins.loc[:, columns_to_select] pumpkins.dropna(inplace=True)תמיד אפשר להציץ במאגר הנתונים החדש שלכם:
pumpkins.info
הדמיה - תרשים קטגוריאלי
עד עכשיו טענתם את מחברת ההתחלה עם נתוני הדלעות שוב וניקיתם אותה כך שתשמר מאגר נתונים המכיל כמה משתנים, כולל Color. בואו נדמיין את מאגר הנתונים במחברת באמצעות ספרייה אחרת: Seaborn, שנבנתה על Matplotlib שבה השתמשנו קודם.
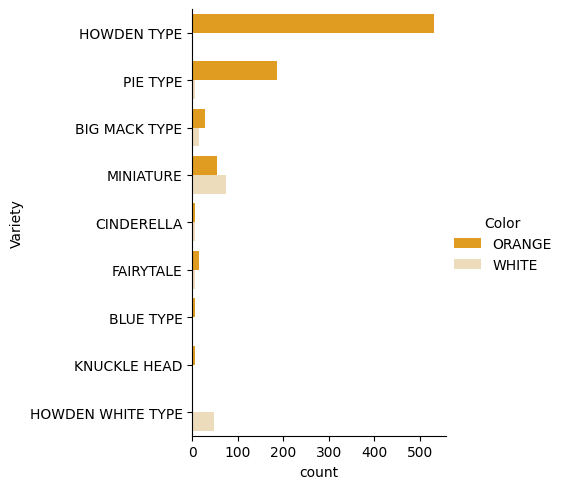
Seaborn מציעה דרכים מעניינות להדמיית הנתונים שלכם. לדוגמה, אפשר להשוות את התפלגות הנתונים עבור כל Variety ו-Color בתרשים קטגוריאלי.
-
צרו תרשים כזה באמצעות הפונקציה
catplot, תוך שימוש בנתוני הדלעות שלנוpumpkins, והגדירו מיפוי צבעים לכל קטגוריית דלעת (כתום או לבן):import seaborn as sns palette = { 'ORANGE': 'orange', 'WHITE': 'wheat', } sns.catplot( data=pumpkins, y="Variety", hue="Color", kind="count", palette=palette, )בהתבוננות בנתונים, אפשר לראות כיצד נתוני הצבע קשורים לזן.
✅ בהתבסס על התרשים הקטגוריאלי הזה, אילו חקירות מעניינות אתם יכולים לדמיין?
עיבוד נתונים: קידוד תכונות ותוויות
מאגר הנתונים של הדלעות שלנו מכיל ערכי מחרוזת עבור כל העמודות שלו. עבודה עם נתונים קטגוריאליים היא אינטואיטיבית עבור בני אדם אך לא עבור מכונות. אלגוריתמים של למידת מכונה עובדים טוב עם מספרים. לכן קידוד הוא שלב חשוב מאוד בשלב עיבוד הנתונים, מכיוון שהוא מאפשר לנו להפוך נתונים קטגוריאליים לנתונים מספריים, מבלי לאבד מידע. קידוד טוב מוביל לבניית מודל טוב.
לקידוד תכונות יש שני סוגים עיקריים של מקודדים:
-
מקודד אורדינלי: מתאים היטב למשתנים אורדינליים, שהם משתנים קטגוריאליים שבהם הנתונים שלהם עוקבים אחר סדר לוגי, כמו עמודת
Item Sizeבמאגר הנתונים שלנו. הוא יוצר מיפוי כך שכל קטגוריה מיוצגת על ידי מספר, שהוא הסדר של הקטגוריה בעמודה.from sklearn.preprocessing import OrdinalEncoder item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']] ordinal_features = ['Item Size'] ordinal_encoder = OrdinalEncoder(categories=item_size_categories) -
מקודד קטגוריאלי: מתאים היטב למשתנים נומינליים, שהם משתנים קטגוריאליים שבהם הנתונים שלהם אינם עוקבים אחר סדר לוגי, כמו כל התכונות השונות מ-
Item Sizeבמאגר הנתונים שלנו. זהו קידוד one-hot, כלומר כל קטגוריה מיוצגת על ידי עמודה בינארית: המשתנה המקודד שווה ל-1 אם הדלעת שייכת לזן הזה ול-0 אחרת.from sklearn.preprocessing import OneHotEncoder categorical_features = ['City Name', 'Package', 'Variety', 'Origin'] categorical_encoder = OneHotEncoder(sparse_output=False)
לאחר מכן, משתמשים ב-ColumnTransformer כדי לשלב מספר מקודדים לשלב אחד וליישם אותם על העמודות המתאימות.
from sklearn.compose import ColumnTransformer
ct = ColumnTransformer(transformers=[
('ord', ordinal_encoder, ordinal_features),
('cat', categorical_encoder, categorical_features)
])
ct.set_output(transform='pandas')
encoded_features = ct.fit_transform(pumpkins)
מצד שני, לקידוד התווית, משתמשים במחלקת LabelEncoder של scikit-learn, שהיא מחלקת עזר לנרמל תוויות כך שיכילו רק ערכים בין 0 ל-n_classes-1 (כאן, 0 ו-1).
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
encoded_label = label_encoder.fit_transform(pumpkins['Color'])
לאחר שקידדנו את התכונות והתווית, אפשר למזג אותן למאגר נתונים חדש encoded_pumpkins.
encoded_pumpkins = encoded_features.assign(Color=encoded_label)
✅ מה היתרונות של שימוש במקודד אורדינלי עבור עמודת Item Size?
ניתוח קשרים בין משתנים
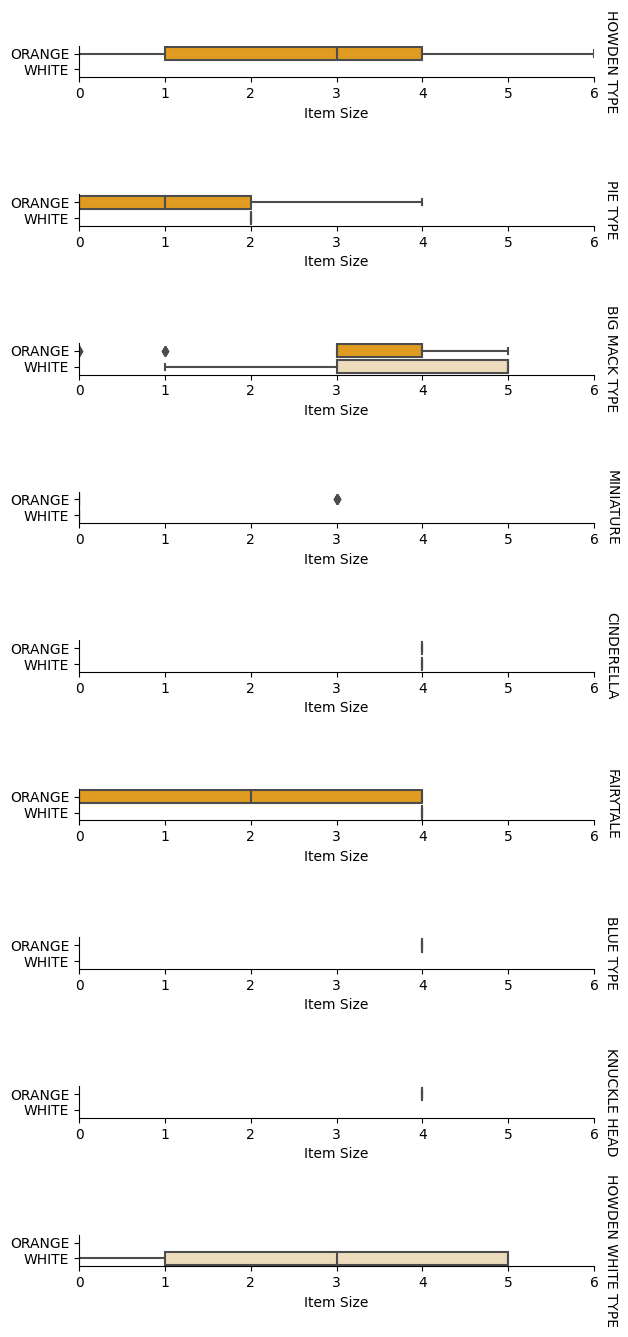
עכשיו, לאחר שעיבדנו את הנתונים שלנו, אפשר לנתח את הקשרים בין התכונות לתווית כדי להבין עד כמה המודל יוכל לחזות את התווית בהתבסס על התכונות. הדרך הטובה ביותר לבצע ניתוח כזה היא באמצעות הדמיית הנתונים. נשתמש שוב בפונקציה catplot של Seaborn, כדי להמחיש את הקשרים בין Item Size, Variety ו-Color בתרשים קטגוריאלי. כדי להמחיש את הנתונים טוב יותר נשתמש בעמודת Item Size המקודדת ובעמודת Variety הלא מקודדת.
palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}
pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']
g = sns.catplot(
data=pumpkins,
x="Item Size", y="Color", row='Variety',
kind="box", orient="h",
sharex=False, margin_titles=True,
height=1.8, aspect=4, palette=palette,
)
g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
g.set_titles(row_template="{row_name}")
שימוש בתרשים swarm
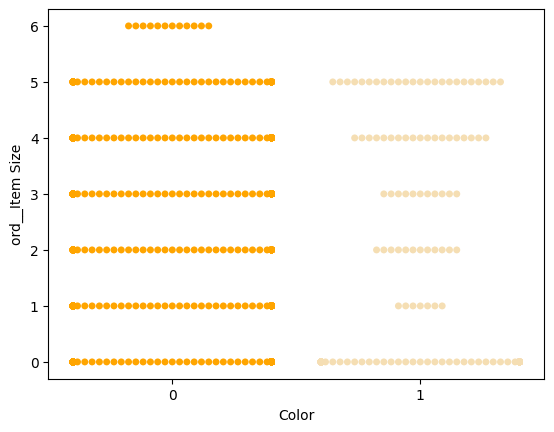
מכיוון ש-Color הוא קטגוריה בינארית (לבן או לא), הוא דורש 'גישה מיוחדת להדמיה'. יש דרכים אחרות להמחיש את הקשר של קטגוריה זו עם משתנים אחרים.
אפשר להמחיש משתנים זה לצד זה עם תרשימי Seaborn.
-
נסו תרשים 'swarm' כדי להראות את התפלגות הערכים:
palette = { 0: 'orange', 1: 'wheat' } sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)
שימו לב: הקוד למעלה עשוי ליצור אזהרה, מכיוון ש-Seaborn מתקשה לייצג כמות כזו של נקודות נתונים בתרשים swarm. פתרון אפשרי הוא להקטין את גודל הסמן, באמצעות הפרמטר 'size'. עם זאת, שימו לב שזה משפיע על קריאות התרשים.
🧮 תראו לי את המתמטיקה
רגרסיה לוגיסטית מתבססת על הרעיון של 'סבירות מרבית' באמצעות פונקציות סיגמואיד. פונקציית סיגמואיד על תרשים נראית כמו צורת 'S'. היא לוקחת ערך וממפה אותו למקום בין 0 ל-1. העקומה שלה נקראת גם 'עקומה לוגיסטית'. הנוסחה שלה נראית כך:
כאשר נקודת האמצע של הסיגמואיד נמצאת בנקודת ה-0 של x, L הוא הערך המרבי של העקומה, ו-k הוא תלילות העקומה. אם תוצאת הפונקציה היא יותר מ-0.5, התווית המדוברת תינתן למעמד '1' של הבחירה הבינארית. אם לא, היא תסווג כ-'0'.
בניית המודל שלכם
בניית מודל למציאת סיווגים בינאריים היא פשוטה באופן מפתיע ב-Scikit-learn.
🎥 לחצו על התמונה למעלה לסרטון קצר על בניית מודל רגרסיה ליניארית.
-
בחרו את המשתנים שתרצו להשתמש בהם במודל הסיווג שלכם וחלקו את קבוצות האימון והבדיקה באמצעות קריאה ל-
train_test_split():from sklearn.model_selection import train_test_split X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])] y = encoded_pumpkins['Color'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) -
עכשיו אפשר לאמן את המודל, באמצעות קריאה ל-
fit()עם נתוני האימון שלכם, ולהדפיס את התוצאה שלו:from sklearn.metrics import f1_score, classification_report from sklearn.linear_model import LogisticRegression model = LogisticRegression() model.fit(X_train, y_train) predictions = model.predict(X_test) print(classification_report(y_test, predictions)) print('Predicted labels: ', predictions) print('F1-score: ', f1_score(y_test, predictions))הסתכלו על לוח התוצאות של המודל שלכם. הוא לא רע, בהתחשב בכך שיש לכם רק כ-1000 שורות נתונים:
precision recall f1-score support 0 0.94 0.98 0.96 166 1 0.85 0.67 0.75 33 accuracy 0.92 199 macro avg 0.89 0.82 0.85 199 weighted avg 0.92 0.92 0.92 199 Predicted labels: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1] F1-score: 0.7457627118644068
הבנה טובה יותר באמצעות מטריצת בלבול
בעוד שאפשר לקבל דוח תוצאות מונחים על ידי הדפסת הפריטים למעלה, ייתכן שתוכלו להבין את המודל שלכם ביתר קלות באמצעות מטריצת בלבול שתעזור לנו להבין כיצד המודל מתפקד.
🎓 'מטריצת בלבול' (או 'מטריצת שגיאות') היא טבלה שמבטאת את החיוביים והשליליים האמיתיים מול השגויים של המודל שלכם, ובכך מעריכה את דיוק התחזיות.
-
כדי להשתמש במטריצת בלבול, קראו ל-
confusion_matrix():from sklearn.metrics import confusion_matrix confusion_matrix(y_test, predictions)הסתכלו על מטריצת הבלבול של המודל שלכם:
array([[162, 4], [ 11, 22]])
ב-Scikit-learn, שורות (axis 0) הן תוויות אמיתיות ועמודות (axis 1) הן תוויות חזויות.
| 0 | 1 | |
|---|---|---|
| 0 | TN | FP |
| 1 | FN | TP |
מה קורה כאן? נניח שהמודל שלנו מתבקש לסווג דלעות בין שתי קטגוריות בינאריות, קטגוריה 'לבן' וקטגוריה 'לא-לבן'.
- אם המודל שלכם חוזה דלעת כלא לבנה והיא שייכת לקטגוריה 'לא-לבן' במציאות, אנחנו קוראים לזה שלילי אמיתי (True Negative), שמוצג על ידי המספר בפינה השמאלית העליונה.
- אם המודל שלכם חוזה דלעת כלבנה והיא שייכת לקטגוריה 'לא-לבן' במציאות, אנחנו קוראים לזה שלילי שגוי (False Negative), שמוצג על ידי המספר בפינה השמאלית התחתונה.
- אם המודל שלכם חוזה דלעת כלא לבנה והיא שייכת לקטגוריה 'לבן' במציאות, אנחנו קוראים לזה חיובי שגוי (False Positive), שמוצג על ידי המספר בפינה הימנית העליונה.
- אם המודל שלכם חוזה דלעת כלבנה והיא שייכת לקטגוריה 'לבן' במציאות, אנחנו קוראים לזה חיובי אמיתי (True Positive), שמוצג על ידי המספר בפינה הימנית התחתונה.
כפי שכנראה ניחשתם, עדיף שיהיו יותר חיוביים אמיתיים ושליליים אמיתיים ומספר נמוך יותר של חיוביים שגויים ושליליים שגויים, מה שמעיד על כך שהמודל מתפקד טוב יותר. כיצד מטריצת הבלבול קשורה לדיוק ולשליפה? זכרו, דוח הסיווג שהודפס למעלה הציג דיוק (0.85) ושליפה (0.67).
דיוק = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461
שליפה = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666
✅ ש: לפי מטריצת הבלבול, איך המודל ביצע? ת: לא רע; יש מספר טוב של שליליים אמיתיים אבל גם כמה שליליים שגויים.
בואו נחזור למונחים שראינו קודם בעזרת המיפוי של TP/TN ו-FP/FN במטריצת הבלבול:
🎓 דיוק: TP/(TP + FP) החלק של המקרים הרלוונטיים מתוך המקרים שנמצאו (לדוגמה, אילו תוויות סווגו היטב).
🎓 שליפה: TP/(TP + FN) החלק של המקרים הרלוונטיים שנמצאו, בין אם סווגו היטב או לא.
🎓 ציון f1: (2 * דיוק * שליפה)/(דיוק + שליפה) ממוצע משוקלל של דיוק ושליפה, כאשר הטוב ביותר הוא 1 והגרוע ביותר הוא 0.
🎓 תמיכה: מספר המופעים של כל תווית שנמצאה.
🎓 דיוק כללי: (TP + TN)/(TP + TN + FP + FN) אחוז התוויות שסווגו בצורה מדויקת עבור דגימה.
🎓 ממוצע מאקרו: חישוב הממוצע הלא משוקלל של המדדים עבור כל תווית, מבלי להתחשב באי-איזון בין התוויות.
🎓 ממוצע משוקלל: חישוב הממוצע של המדדים עבור כל תווית, תוך התחשבות באי-איזון בין התוויות על ידי שקילתן לפי התמיכה (מספר המקרים האמיתיים עבור כל תווית).
✅ האם אתם יכולים לחשוב על איזה מדד כדאי להתמקד אם אתם רוצים שהמודל יפחית את מספר השליליים השגויים?
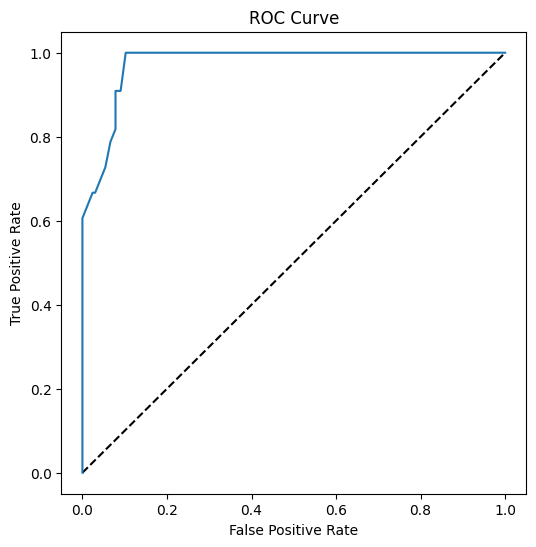
ויזואליזציה של עקומת ROC של המודל הזה
🎥 לחצו על התמונה למעלה לצפייה בסרטון קצר על עקומות ROC
בואו נעשה ויזואליזציה נוספת כדי לראות את מה שנקרא 'עקומת ROC':
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])
fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()
באמצעות Matplotlib, שרטטו את Receiving Operating Characteristic או ROC של המודל. עקומות ROC משמשות לעיתים קרובות כדי לקבל מבט על תוצאות מסווג במונחים של חיוביים אמיתיים מול חיוביים שגויים. "עקומות ROC מציגות בדרך כלל את שיעור החיוביים האמיתיים על ציר ה-Y, ואת שיעור החיוביים השגויים על ציר ה-X." לכן, תלילות העקומה והמרחק בין קו האמצע לעקומה חשובים: אתם רוצים עקומה שמתקדמת במהירות למעלה ומעל הקו. במקרה שלנו, יש חיוביים שגויים בהתחלה, ואז הקו מתקדם למעלה ומעל בצורה נכונה:
לבסוף, השתמשו ב-API של roc_auc_score של Scikit-learn כדי לחשב את 'שטח מתחת לעקומה' (AUC):
auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)
התוצאה היא 0.9749908725812341. מכיוון ש-AUC נע בין 0 ל-1, אתם רוצים ציון גבוה, שכן מודל שמנבא בצורה נכונה ב-100% יקבל AUC של 1; במקרה הזה, המודל די טוב.
בשיעורים עתידיים על סיווגים, תלמדו כיצד לשפר את ציוני המודל שלכם. אבל לעת עתה, ברכות! סיימתם את שיעורי הרגרסיה האלה!
🚀אתגר
יש עוד הרבה ללמוד על רגרסיה לוגיסטית! אבל הדרך הטובה ביותר ללמוד היא להתנסות. מצאו מערך נתונים שמתאים לסוג זה של ניתוח ובנו מודל איתו. מה אתם לומדים? טיפ: נסו Kaggle עבור מערכי נתונים מעניינים.
מבחן לאחר השיעור
סקירה ולימוד עצמי
קראו את העמודים הראשונים של המאמר הזה מסטנפורד על שימושים מעשיים לרגרסיה לוגיסטית. חשבו על משימות שמתאימות יותר לאחד מסוגי הרגרסיה שלמדנו עד כה. מה יעבוד הכי טוב?
משימה
כתב ויתור:
מסמך זה תורגם באמצעות שירות תרגום מבוסס בינה מלאכותית Co-op Translator. למרות שאנו שואפים לדיוק, יש לקחת בחשבון שתרגומים אוטומטיים עשויים להכיל שגיאות או אי דיוקים. המסמך המקורי בשפתו המקורית צריך להיחשב כמקור סמכותי. עבור מידע קריטי, מומלץ להשתמש בתרגום מקצועי על ידי אדם. איננו נושאים באחריות לאי הבנות או לפרשנויות שגויות הנובעות משימוש בתרגום זה.