36 KiB

Raw Permalink Blame History Unescape Escape

Εισαγωγή στην ομαδοποίηση

Η ομαδοποίηση είναι ένας τύπος Μη Εποπτευόμενης Μάθησης που υποθέτει ότι ένα σύνολο δεδομένων είναι μη επισημασμένο ή ότι οι είσοδοι του δεν αντιστοιχούν σε προκαθορισμένες εξόδους. Χρησιμοποιεί διάφορους αλγόριθμους για να ταξινομήσει μη επισημασμένα δεδομένα και να παρέχει ομάδες σύμφωνα με τα μοτίβα που εντοπίζει στα δεδομένα.

🎥 Κάντε κλικ στην εικόνα παραπάνω για ένα βίντεο. Ενώ μελετάτε τη μηχανική μάθηση με την ομαδοποίηση, απολαύστε μερικά κομμάτια Nigerian Dance Hall - αυτό είναι ένα πολύ δημοφιλές τραγούδι από το 2014 από τους PSquare.

Κουίζ πριν το μάθημα

Εισαγωγή

Η ομαδοποίηση είναι πολύ χρήσιμη για την εξερεύνηση δεδομένων. Ας δούμε αν μπορεί να βοηθήσει στην ανακάλυψη τάσεων και μοτίβων στον τρόπο που το κοινό της Νιγηρίας καταναλώνει μουσική.

✅ Σκεφτείτε για ένα λεπτό τις χρήσεις της ομαδοποίησης. Στην καθημερινή ζωή, η ομαδοποίηση συμβαίνει κάθε φορά που έχετε έναν σωρό από ρούχα και πρέπει να ταξινομήσετε τα ρούχα των μελών της οικογένειάς σας 🧦👕👖🩲. Στην επιστήμη δεδομένων, η ομαδοποίηση συμβαίνει όταν προσπαθείτε να αναλύσετε τις προτιμήσεις ενός χρήστη ή να προσδιορίσετε τα χαρακτηριστικά οποιουδήποτε μη επισημασμένου συνόλου δεδομένων. Η ομαδοποίηση, με έναν τρόπο, βοηθά να βάλουμε τάξη στο χάος, όπως ένα συρτάρι με κάλτσες.

🎥 Κάντε κλικ στην εικόνα παραπάνω για ένα βίντεο: Ο John Guttag από το MIT παρουσιάζει την ομαδοποίηση.

Σε επαγγελματικό περιβάλλον, η ομαδοποίηση μπορεί να χρησιμοποιηθεί για τον καθορισμό πραγμάτων όπως η τμηματοποίηση της αγοράς, για παράδειγμα, για να προσδιοριστεί ποιες ηλικιακές ομάδες αγοράζουν ποια προϊόντα. Μια άλλη χρήση θα μπορούσε να είναι η ανίχνευση ανωμαλιών, ίσως για την ανίχνευση απάτης από ένα σύνολο δεδομένων συναλλαγών πιστωτικών καρτών. Ή μπορεί να χρησιμοποιήσετε την ομαδοποίηση για να προσδιορίσετε όγκους σε μια παρτίδα ιατρικών σαρώσεων.

✅ Σκεφτείτε για ένα λεπτό πώς μπορεί να έχετε συναντήσει την ομαδοποίηση 'στην πράξη', σε τραπεζικό, ηλεκτρονικό εμπόριο ή επιχειρηματικό περιβάλλον.

🎓 Ενδιαφέρον είναι ότι η ανάλυση ομαδοποίησης ξεκίνησε στους τομείς της Ανθρωπολογίας και της Ψυχολογίας τη δεκαετία του 1930. Μπορείτε να φανταστείτε πώς μπορεί να έχει χρησιμοποιηθεί;

Εναλλακτικά, θα μπορούσατε να τη χρησιμοποιήσετε για την ομαδοποίηση αποτελεσμάτων αναζήτησης - για παράδειγμα, ανάμεσα σε συνδέσμους αγορών, εικόνες ή κριτικές. Η ομαδοποίηση είναι χρήσιμη όταν έχετε ένα μεγάλο σύνολο δεδομένων που θέλετε να μειώσετε και στο οποίο θέλετε να πραγματοποιήσετε πιο λεπτομερή ανάλυση, ώστε η τεχνική να μπορεί να χρησιμοποιηθεί για να μάθετε περισσότερα για τα δεδομένα πριν κατασκευαστούν άλλα μοντέλα.

✅ Μόλις τα δεδομένα σας οργανωθούν σε ομάδες, τους αναθέτετε ένα Id ομάδας, και αυτή η τεχνική μπορεί να είναι χρήσιμη για τη διατήρηση της ιδιωτικότητας ενός συνόλου δεδομένων. Μπορείτε να αναφέρεστε σε ένα σημείο δεδομένων με το Id της ομάδας του, αντί για πιο αποκαλυπτικά αναγνωρίσιμα δεδομένα. Μπορείτε να σκεφτείτε άλλους λόγους για τους οποίους θα αναφερόσασταν σε ένα Id ομάδας αντί για άλλα στοιχεία της ομάδας για να το αναγνωρίσετε;

Εμβαθύνετε την κατανόησή σας για τις τεχνικές ομαδοποίησης σε αυτήν την ενότητα εκμάθησης.

Ξεκινώντας με την ομαδοποίηση

Το Scikit-learn προσφέρει μια μεγάλη ποικιλία μεθόδων για την εκτέλεση ομαδοποίησης. Ο τύπος που θα επιλέξετε θα εξαρτηθεί από την περίπτωση χρήσης σας. Σύμφωνα με την τεκμηρίωση, κάθε μέθοδος έχει διάφορα πλεονεκτήματα. Ακολουθεί ένας απλοποιημένος πίνακας των μεθόδων που υποστηρίζονται από το Scikit-learn και οι κατάλληλες περιπτώσεις χρήσης τους:

Όνομα μεθόδου	Περίπτωση χρήσης
K-Means	γενική χρήση, επαγωγική
Affinity propagation	πολλές, άνισες ομάδες, επαγωγική
Mean-shift	πολλές, άνισες ομάδες, επαγωγική
Spectral clustering	λίγες, ίσες ομάδες, μεταγωγική
Ward hierarchical clustering	πολλές, περιορισμένες ομάδες, μεταγωγική
Agglomerative clustering	πολλές, περιορισμένες, μη Ευκλείδειες αποστάσεις, μεταγωγική
DBSCAN	μη επίπεδη γεωμετρία, άνισες ομάδες, μεταγωγική
OPTICS	μη επίπεδη γεωμετρία, άνισες ομάδες με μεταβλητή πυκνότητα, μεταγωγική
Gaussian mixtures	επίπεδη γεωμετρία, επαγωγική
BIRCH	μεγάλο σύνολο δεδομένων με εξαιρέσεις, επαγωγική

🎓 Ο τρόπος με τον οποίο δημιουργούμε ομάδες έχει να κάνει πολύ με το πώς συγκεντρώνουμε τα σημεία δεδομένων σε ομάδες. Ας αναλύσουμε μερικές έννοιες:

🎓 'Μεταγωγική' vs. 'Επαγωγική'

Η μεταγωγική συμπερασματολογία προκύπτει από παρατηρούμενες περιπτώσεις εκπαίδευσης που αντιστοιχούν σε συγκεκριμένες περιπτώσεις δοκιμής. Η επαγωγική συμπερασματολογία προκύπτει από περιπτώσεις εκπαίδευσης που αντιστοιχούν σε γενικούς κανόνες, οι οποίοι στη συνέχεια εφαρμόζονται σε περιπτώσεις δοκιμής.

Ένα παράδειγμα: Φανταστείτε ότι έχετε ένα σύνολο δεδομένων που είναι μόνο εν μέρει επισημασμένο. Κάποια πράγματα είναι 'δίσκοι', κάποια 'cds', και κάποια είναι κενά. Η δουλειά σας είναι να παρέχετε ετικέτες για τα κενά. Αν επιλέξετε μια επαγωγική προσέγγιση, θα εκπαιδεύσετε ένα μοντέλο που αναζητά 'δίσκους' και 'cds', και θα εφαρμόσετε αυτές τις ετικέτες στα μη επισημασμένα δεδομένα σας. Αυτή η προσέγγιση θα δυσκολευτεί να ταξινομήσει πράγματα που είναι στην πραγματικότητα 'κασέτες'. Μια μεταγωγική προσέγγιση, από την άλλη πλευρά, χειρίζεται αυτά τα άγνωστα δεδομένα πιο αποτελεσματικά καθώς εργάζεται για να ομαδοποιήσει παρόμοια αντικείμενα μαζί και στη συνέχεια εφαρμόζει μια ετικέτα σε μια ομάδα. Σε αυτήν την περίπτωση, οι ομάδες μπορεί να αντικατοπτρίζουν 'στρογγυλά μουσικά αντικείμενα' και 'τετράγωνα μουσικά αντικείμενα'.

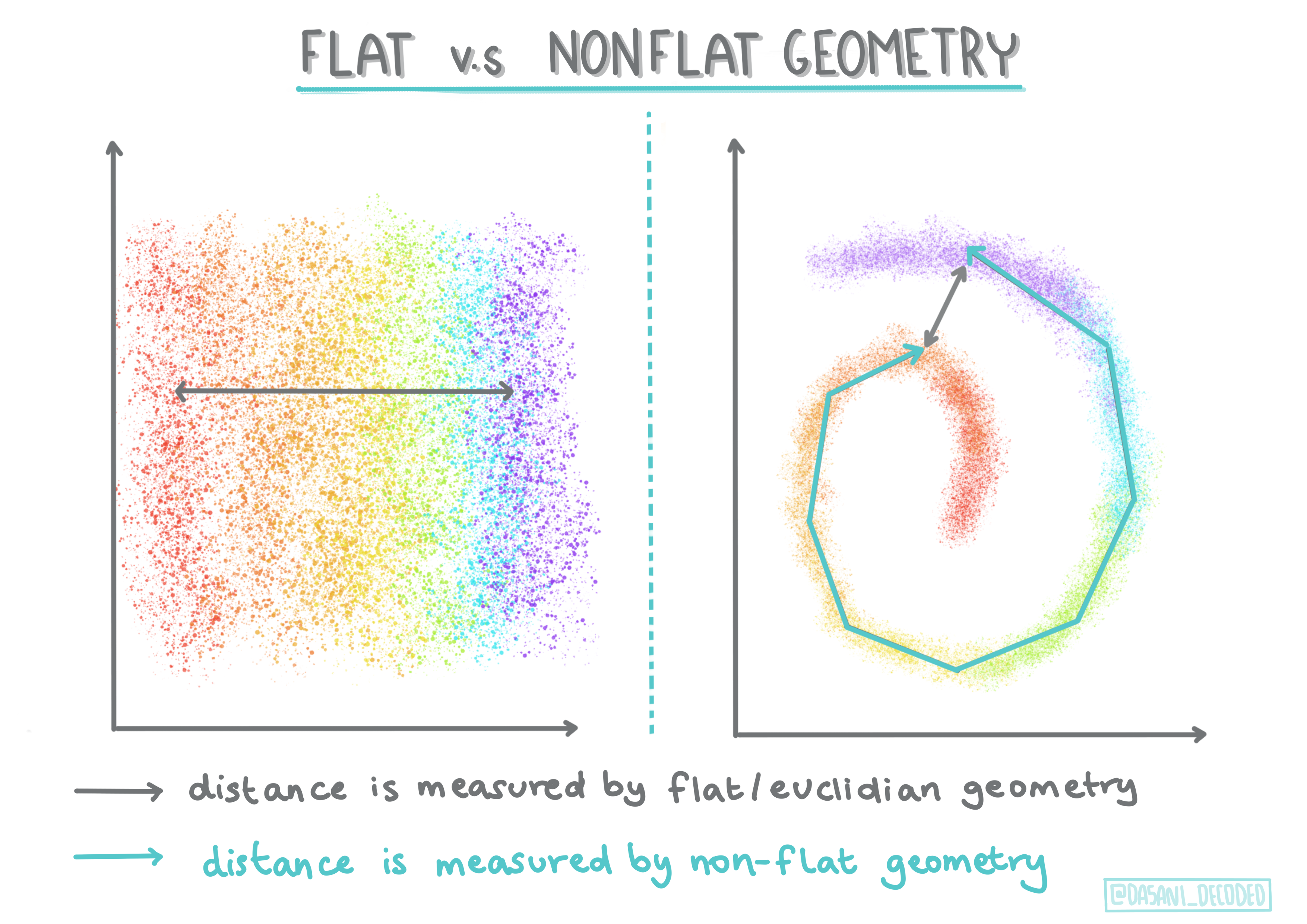
🎓 'Μη επίπεδη' vs. 'Επίπεδη' γεωμετρία

Προερχόμενη από τη μαθηματική ορολογία, η μη επίπεδη vs. επίπεδη γεωμετρία αναφέρεται στη μέτρηση των αποστάσεων μεταξύ σημείων είτε με 'επίπεδη' (Ευκλείδεια) είτε με 'μη επίπεδη' (μη Ευκλείδεια) γεωμετρικές μεθόδους.

'Επίπεδη' σε αυτό το πλαίσιο αναφέρεται στην Ευκλείδεια γεωμετρία (μέρη της οποίας διδάσκονται ως 'επίπεδη' γεωμετρία), και μη επίπεδη αναφέρεται στη μη Ευκλείδεια γεωμετρία. Τι σχέση έχει η γεωμετρία με τη μηχανική μάθηση; Λοιπόν, ως δύο πεδία που βασίζονται στα μαθηματικά, πρέπει να υπάρχει ένας κοινός τρόπος μέτρησης των αποστάσεων μεταξύ σημείων σε ομάδες, και αυτό μπορεί να γίνει με 'επίπεδο' ή 'μη επίπεδο' τρόπο, ανάλογα με τη φύση των δεδομένων. Ευκλείδειες αποστάσεις μετρώνται ως το μήκος ενός τμήματος γραμμής μεταξύ δύο σημείων. Μη Ευκλείδειες αποστάσεις μετρώνται κατά μήκος μιας καμπύλης. Αν τα δεδομένα σας, οπτικοποιημένα, φαίνεται να μην υπάρχουν σε ένα επίπεδο, μπορεί να χρειαστεί να χρησιμοποιήσετε έναν εξειδικευμένο αλγόριθμο για να τα χειριστείτε.

Infographic από Dasani Madipalli

🎓 'Αποστάσεις'

Οι ομάδες ορίζονται από τη μήτρα αποστάσεων τους, π.χ. τις αποστάσεις μεταξύ σημείων. Αυτή η απόσταση μπορεί να μετρηθεί με διάφορους τρόπους. Οι Ευκλείδειες ομάδες ορίζονται από τον μέσο όρο των τιμών των σημείων και περιέχουν ένα 'κέντρο' ή κεντρικό σημείο. Οι αποστάσεις μετρώνται έτσι από την απόσταση από αυτό το κέντρο. Οι μη Ευκλείδειες αποστάσεις αναφέρονται σε 'clustroids', το σημείο που είναι πιο κοντά σε άλλα σημεία. Τα clustroids με τη σειρά τους μπορούν να οριστούν με διάφορους τρόπους.

🎓 'Περιορισμένες'

Η Περιορισμένη Ομαδοποίηση εισάγει 'ημι-εποπτευόμενη' μάθηση σε αυτήν τη μη εποπτευόμενη μέθοδο. Οι σχέσεις μεταξύ σημείων επισημαίνονται ως 'δεν μπορούν να συνδεθούν' ή 'πρέπει να συνδεθούν', ώστε να επιβληθούν κάποιοι κανόνες στο σύνολο δεδομένων.

Ένα παράδειγμα: Αν ένας αλγόριθμος αφεθεί ελεύθερος σε μια παρτίδα μη επισημασμένων ή ημι-επισημασμένων δεδομένων, οι ομάδες που παράγει μπορεί να είναι χαμηλής ποιότητας. Στο παραπάνω παράδειγμα, οι ομάδες μπορεί να ομαδοποιούν 'στρογγυλά μουσικά αντικείμενα' και 'τετράγωνα μουσικά αντικείμενα' και 'τριγωνικά αντικείμενα' και 'μπισκότα'. Αν δοθούν κάποιοι περιορισμοί ή κανόνες για να ακολουθήσει ("το αντικείμενο πρέπει να είναι φτιαγμένο από πλαστικό", "το αντικείμενο πρέπει να μπορεί να παράγει μουσική") αυτό μπορεί να βοηθήσει να 'περιορίσει' τον αλγόριθμο να κάνει καλύτερες επιλογές.

🎓 'Πυκνότητα'

Δεδομένα που είναι 'θορυβώδη' θεωρούνται 'πυκνά'. Οι αποστάσεις μεταξύ σημείων σε κάθε μία από τις ομάδες τους μπορεί να αποδειχθούν, κατά την εξέταση, περισσότερο ή λιγότερο πυκνές, ή 'συγκεντρωμένες', και έτσι αυτά τα δεδομένα πρέπει να αναλυθούν με την κατάλληλη μέθοδο ομαδοποίησης. Αυτό το άρθρο δείχνει τη διαφορά μεταξύ της χρήσης των αλγορίθμων K-Means clustering και HDBSCAN για την εξερεύνηση ενός θορυβώδους συνόλου δεδομένων με άνιση πυκνότητα ομάδων.

Αλγόριθμοι ομαδοποίησης

Υπάρχουν πάνω από 100 αλγόριθμοι ομαδοποίησης, και η χρήση τους εξαρτάται από τη φύση των δεδομένων που έχουμε. Ας συζητήσουμε μερικούς από τους κύριους:

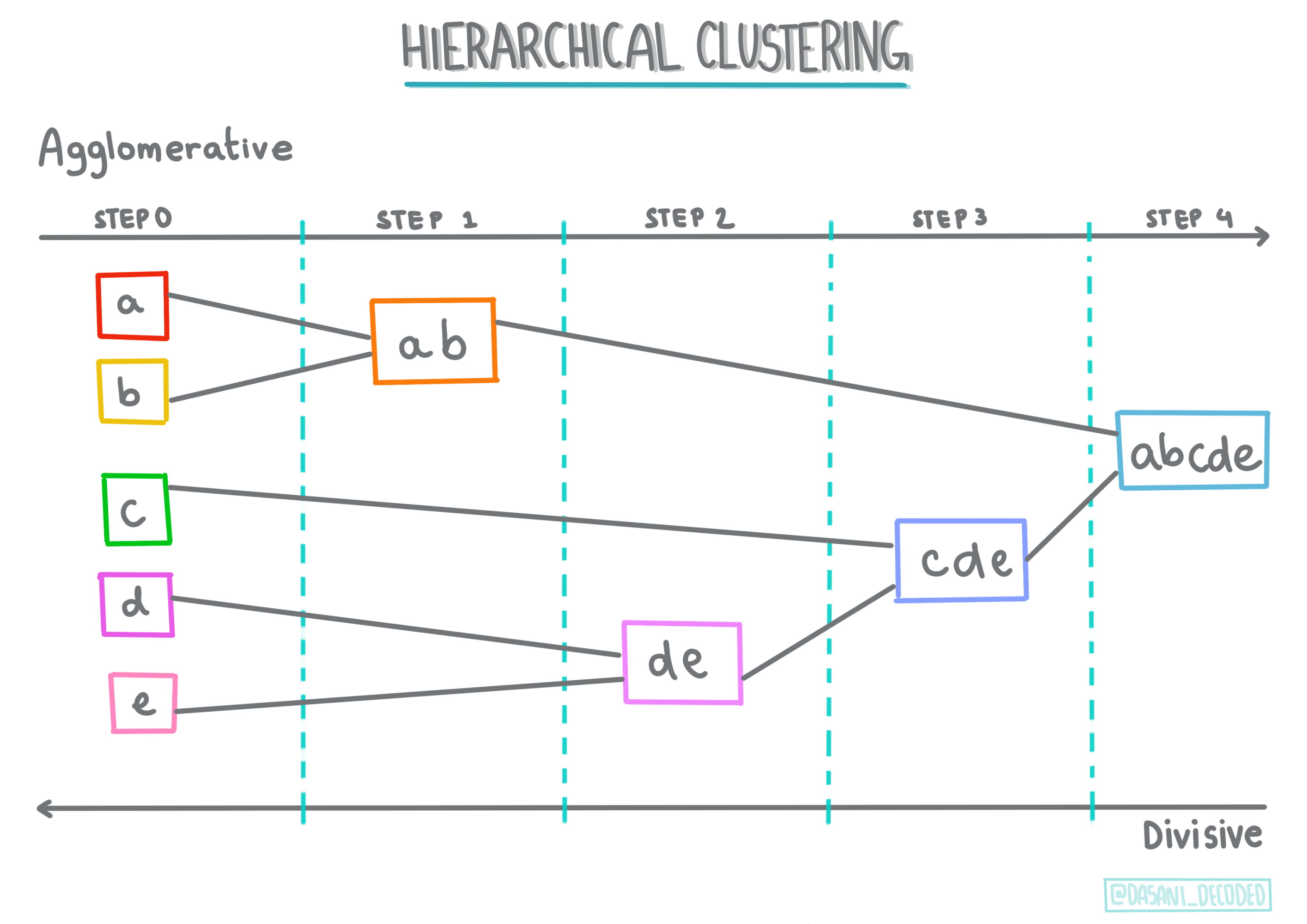
Ιεραρχική ομαδοποίηση. Αν ένα αντικείμενο ταξινομηθεί με βάση την εγγύτητά του σε ένα κοντινό αντικείμενο, αντί για ένα πιο μακρινό, οι ομάδες σχηματίζονται με βάση την απόσταση των μελών τους από και προς άλλα αντικείμενα. Η ιεραρχική ομαδοποίηση του Scikit-learn είναι ιεραρχική.

Infographic από Dasani Madipalli
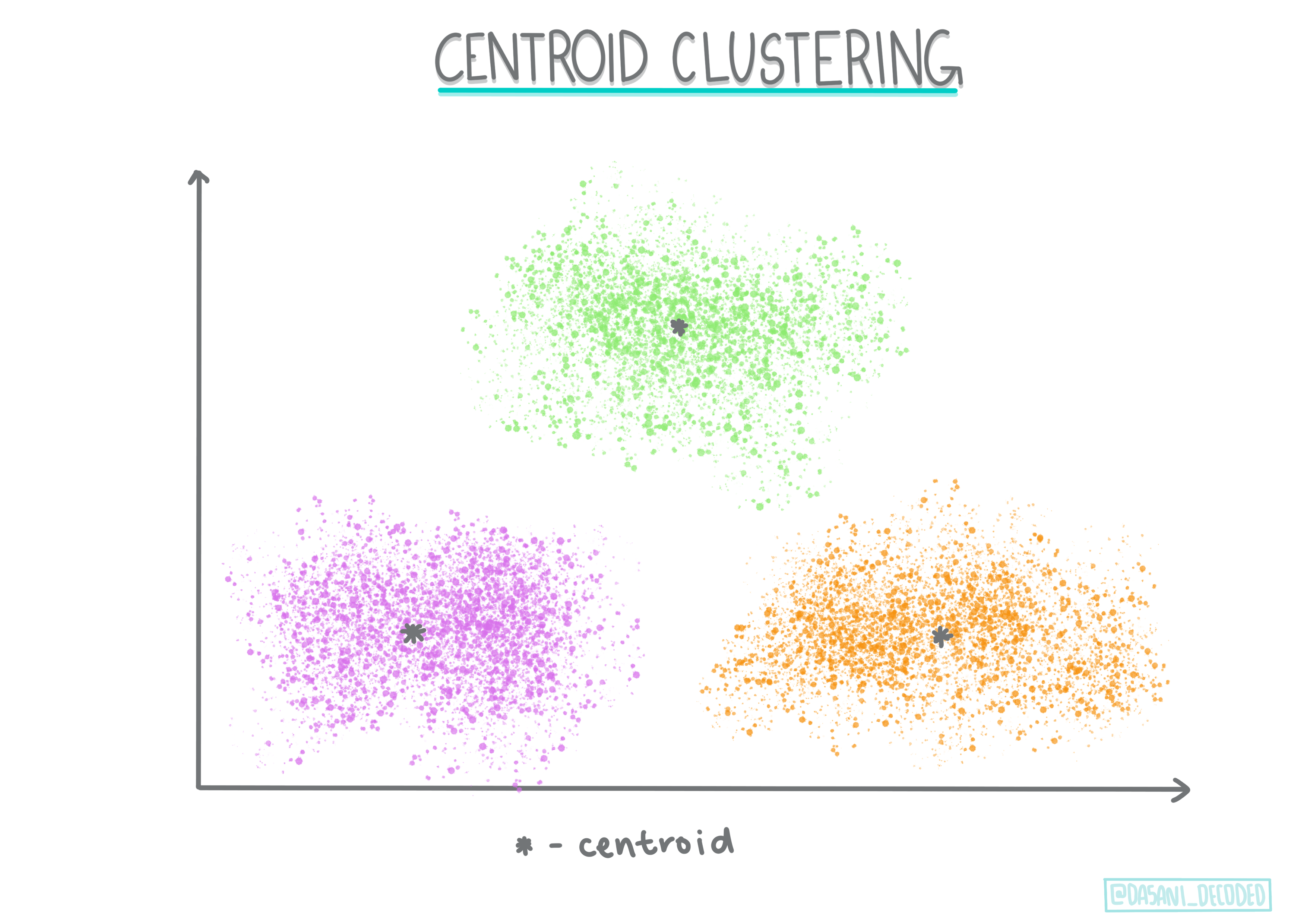
Ομαδοποίηση με κέντρο. Αυτός ο δημοφιλής αλγόριθμος απαιτεί την επιλογή του 'k', ή του αριθμού των ομάδων που θα σχηματιστούν, μετά την οποία ο αλγόριθμος καθορίζει το κεντρικό σημείο μιας ομάδας και συγκεντρώνει δεδομένα γύρω από αυτό το σημείο. Η ομαδοποίηση K-means είναι μια δημοφιλής έκδοση της ομαδοποίησης με κέντρο. Το κέντρο καθορίζεται από τον πλησιέστερο μέσο όρο, εξ ου και το όνομα. Η τετραγωνική απόσταση από την ομάδα ελαχιστοποιείται.

Infographic από Dasani Madipalli
Ομαδοποίηση βάσει κατανομής. Βασισμένη στη στατιστική μοντελοποίηση, η ομαδοποίηση βάσει κατανομής επικεντρώνεται στον καθορισμό της πιθανότητας ότι ένα σημείο δεδομένων ανήκει σε μια ομάδα και το αναθέτει ανάλογα. Οι μέθοδοι Gaussian mixture ανήκουν σε αυτόν τον τύπο.
Ομαδοποίηση βάσει πυκνότητας. Τα σημεία δεδομένων ανατίθενται σε ομάδες με βάση την πυκνότητά τους, ή τη συγκέντρωσή τους γύρω από το ένα το άλλο. Τα σημεία δεδομένων μακριά από την ομάδα θεωρούνται εξαιρέσεις ή θόρυβος. Οι DBSCAN, Mean-shift και OPTICS ανήκουν σε αυτόν τον τύπο ομαδοποίησης.
Ομαδοποίηση βάσει πλέγματος. Για πολυδιάστατα σύνολα δεδομένων, δημιουργείται ένα πλέγμα και τα δεδομένα διαιρούνται μεταξύ των κελιών του πλέγματος, δημιουργώντας έτσι ομάδες.

Άσκηση - ομαδοποιήστε τα δεδομένα σας

Η ομαδοποίηση ως τεχνική βοηθάται πολύ από την κατάλληλη οπτικοποίηση, οπότε ας ξεκινήσουμε οπτικοποιώντας τα μουσικά μας δεδομένα. Αυτή η άσκηση θα μας βοηθήσει να αποφασίσουμε ποια από τις μεθόδους ομαδοποίησης θα πρέπει να χρησιμοποιήσουμε πιο αποτελεσματικά | 2 | LITT! | LITT! | AYLØ | indie r&b | 2018 | 207758 | 40 | 0.836 | 0.272 | 0.564 | 0.000537 | 0.11 | -7.127 | 0.0424 | 130.005 | 4 | | 3 | Confident / Feeling Cool | Enjoy Your Life | Lady Donli | nigerian pop | 2019 | 175135 | 14 | 0.894 | 0.798 | 0.611 | 0.000187 | 0.0964 | -4.961 | 0.113 | 111.087 | 4 | | 4 | wanted you | rare. | Odunsi (The Engine) | afropop | 2018 | 152049 | 25 | 0.702 | 0.116 | 0.833 | 0.91 | 0.348 | -6.044 | 0.0447 | 105.115 | 4 |

Λάβετε κάποιες πληροφορίες για το dataframe, καλώντας info():

df.info()

Η έξοδος μοιάζει κάπως έτσι:

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 530 entries, 0 to 529
Data columns (total 16 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   name              530 non-null    object 
 1   album             530 non-null    object 
 2   artist            530 non-null    object 
 3   artist_top_genre  530 non-null    object 
 4   release_date      530 non-null    int64  
 5   length            530 non-null    int64  
 6   popularity        530 non-null    int64  
 7   danceability      530 non-null    float64
 8   acousticness      530 non-null    float64
 9   energy            530 non-null    float64
 10  instrumentalness  530 non-null    float64
 11  liveness          530 non-null    float64
 12  loudness          530 non-null    float64
 13  speechiness       530 non-null    float64
 14  tempo             530 non-null    float64
 15  time_signature    530 non-null    int64  
dtypes: float64(8), int64(4), object(4)
memory usage: 66.4+ KB

Ελέγξτε ξανά για κενές τιμές, καλώντας isnull() και επαληθεύοντας ότι το άθροισμα είναι 0:

df.isnull().sum()

Όλα φαίνονται καλά:

name                0
album               0
artist              0
artist_top_genre    0
release_date        0
length              0
popularity          0
danceability        0
acousticness        0
energy              0
instrumentalness    0
liveness            0
loudness            0
speechiness         0
tempo               0
time_signature      0
dtype: int64

Περιγράψτε τα δεδομένα:

df.describe()

	release_date	length	popularity	danceability	acousticness	energy	instrumentalness	liveness	loudness	speechiness	tempo	time_signature
count	530	530	530	530	530	530	530	530	530	530	530	530
mean	2015.390566	222298.1698	17.507547	0.741619	0.265412	0.760623	0.016305	0.147308	-4.953011	0.130748	116.487864	3.986792
std	3.131688	39696.82226	18.992212	0.117522	0.208342	0.148533	0.090321	0.123588	2.464186	0.092939	23.518601	0.333701
min	1998	89488	0	0.255	0.000665	0.111	0	0.0283	-19.362	0.0278	61.695	3
25%	2014	199305	0	0.681	0.089525	0.669	0	0.07565	-6.29875	0.0591	102.96125	4
50%	2016	218509	13	0.761	0.2205	0.7845	0.000004	0.1035	-4.5585	0.09795	112.7145	4
75%	2017	242098.5	31	0.8295	0.403	0.87575	0.000234	0.164	-3.331	0.177	125.03925	4
max	2020	511738	73	0.966	0.954	0.995	0.91	0.811	0.582	0.514	206.007	5

🤔 Εάν δουλεύουμε με clustering, μια μη επιβλεπόμενη μέθοδο που δεν απαιτεί δεδομένα με ετικέτες, γιατί δείχνουμε αυτά τα δεδομένα με ετικέτες; Στη φάση εξερεύνησης δεδομένων, είναι χρήσιμες, αλλά δεν είναι απαραίτητες για να λειτουργήσουν οι αλγόριθμοι clustering. Θα μπορούσατε εξίσου να αφαιρέσετε τις επικεφαλίδες των στηλών και να αναφέρεστε στα δεδομένα με αριθμούς στηλών.

Δείτε τις γενικές τιμές των δεδομένων. Σημειώστε ότι η δημοτικότητα μπορεί να είναι '0', κάτι που δείχνει τραγούδια που δεν έχουν κατάταξη. Ας αφαιρέσουμε αυτά σύντομα.

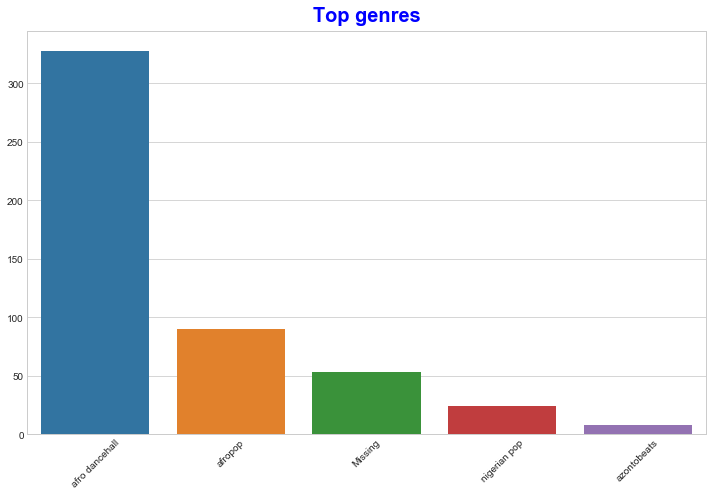
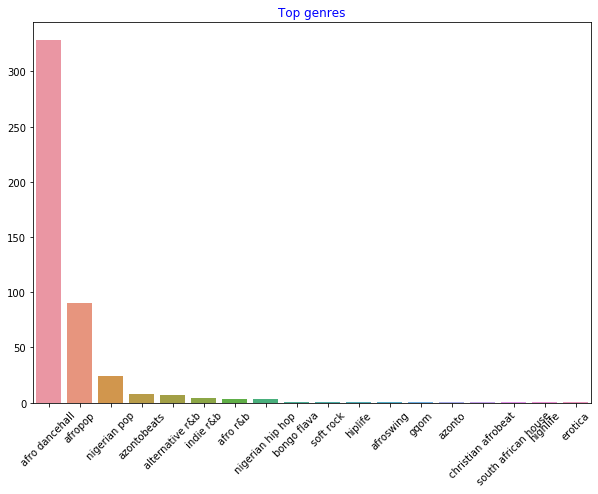
Χρησιμοποιήστε ένα barplot για να βρείτε τα πιο δημοφιλή είδη:

import seaborn as sns

top = df['artist_top_genre'].value_counts()
plt.figure(figsize=(10,7))
sns.barplot(x=top[:5].index,y=top[:5].values)
plt.xticks(rotation=45)
plt.title('Top genres',color = 'blue')

✅ Εάν θέλετε να δείτε περισσότερες κορυφαίες τιμές, αλλάξτε το top [:5] σε μεγαλύτερη τιμή ή αφαιρέστε το για να δείτε όλα.

Σημειώστε ότι όταν το κορυφαίο είδος περιγράφεται ως 'Missing', αυτό σημαίνει ότι το Spotify δεν το ταξινόμησε, οπότε ας το αφαιρέσουμε.

Αφαιρέστε τα δεδομένα που λείπουν φιλτράροντάς τα:

df = df[df['artist_top_genre'] != 'Missing']
top = df['artist_top_genre'].value_counts()
plt.figure(figsize=(10,7))
sns.barplot(x=top.index,y=top.values)
plt.xticks(rotation=45)
plt.title('Top genres',color = 'blue')

Τώρα ελέγξτε ξανά τα είδη:

Τα τρία κορυφαία είδη κυριαρχούν σαφώς σε αυτό το dataset. Ας επικεντρωθούμε στα afro dancehall, afropop, και nigerian pop, και επιπλέον φιλτράρουμε το dataset για να αφαιρέσουμε οτιδήποτε έχει τιμή δημοτικότητας 0 (που σημαίνει ότι δεν ταξινομήθηκε με δημοτικότητα στο dataset και μπορεί να θεωρηθεί θόρυβος για τους σκοπούς μας):
```
df = df[(df['artist_top_genre'] == 'afro dancehall') | (df['artist_top_genre'] == 'afropop') | (df['artist_top_genre'] == 'nigerian pop')]
df = df[(df['popularity'] > 0)]
top = df['artist_top_genre'].value_counts()
plt.figure(figsize=(10,7))
sns.barplot(x=top.index,y=top.values)
plt.xticks(rotation=45)
plt.title('Top genres',color = 'blue')
```
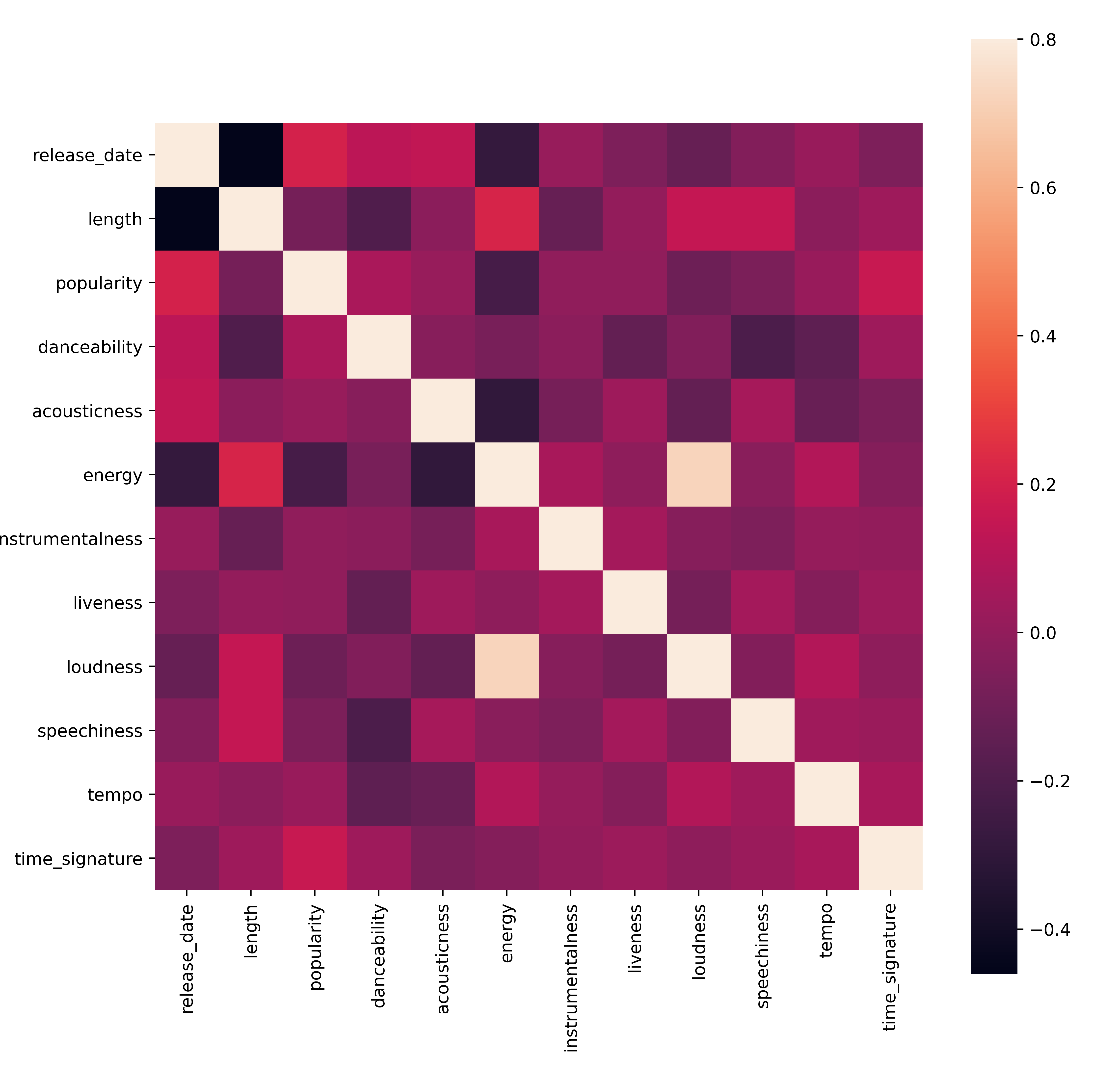
Κάντε μια γρήγορη δοκιμή για να δείτε αν τα δεδομένα συσχετίζονται με κάποιο ιδιαίτερα ισχυρό τρόπο:
```
corrmat = df.corr(numeric_only=True)
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True)
```
Η μόνη ισχυρή συσχέτιση είναι μεταξύ energy και loudness, κάτι που δεν είναι πολύ εκπληκτικό, δεδομένου ότι η δυνατή μουσική είναι συνήθως αρκετά ενεργητική. Κατά τα άλλα, οι συσχετίσεις είναι σχετικά αδύναμες. Θα είναι ενδιαφέρον να δούμε τι μπορεί να κάνει ένας αλγόριθμος clustering με αυτά τα δεδομένα.

🎓 Σημειώστε ότι η συσχέτιση δεν υποδηλώνει αιτιότητα! Έχουμε απόδειξη συσχέτισης αλλά όχι απόδειξη αιτιότητας. Ένας διασκεδαστικός ιστότοπος έχει οπτικοποιήσεις που τονίζουν αυτό το σημείο.

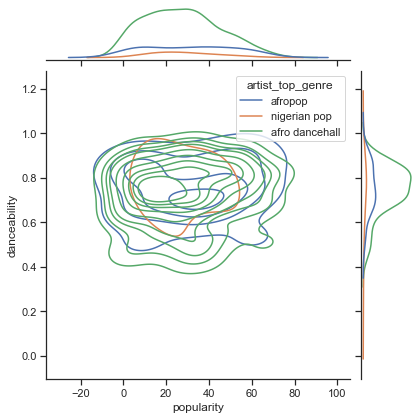
Υπάρχει κάποια σύγκλιση σε αυτό το dataset γύρω από την αντιληπτή δημοτικότητα και την χορευτικότητα ενός τραγουδιού; Ένα FacetGrid δείχνει ότι υπάρχουν ομόκεντροι κύκλοι που ευθυγραμμίζονται, ανεξαρτήτως είδους. Θα μπορούσε να είναι ότι οι νιγηριανές προτιμήσεις συγκλίνουν σε ένα συγκεκριμένο επίπεδο χορευτικότητας για αυτό το είδος;

✅ Δοκιμάστε διαφορετικά σημεία δεδομένων (energy, loudness, speechiness) και περισσότερα ή διαφορετικά μουσικά είδη. Τι μπορείτε να ανακαλύψετε; Ρίξτε μια ματιά στον πίνακα df.describe() για να δείτε τη γενική κατανομή των σημείων δεδομένων.

Άσκηση - κατανομή δεδομένων

Είναι αυτά τα τρία είδη σημαντικά διαφορετικά στην αντίληψη της χορευτικότητάς τους, με βάση τη δημοτικότητά τους;

Εξετάστε την κατανομή δεδομένων των τριών κορυφαίων ειδών μας για τη δημοτικότητα και τη χορευτικότητα κατά μήκος ενός δεδομένου x και y άξονα.
```
sns.set_theme(style="ticks")

g = sns.jointplot(
    data=df,
    x="popularity", y="danceability", hue="artist_top_genre",
    kind="kde",
)
```
Μπορείτε να ανακαλύψετε ομόκεντρους κύκλους γύρω από ένα γενικό σημείο σύγκλισης, που δείχνουν την κατανομή των σημείων.

🎓 Σημειώστε ότι αυτό το παράδειγμα χρησιμοποιεί ένα γράφημα KDE (Kernel Density Estimate) που αναπαριστά τα δεδομένα χρησιμοποιώντας μια συνεχή καμπύλη πυκνότητας πιθανότητας. Αυτό μας επιτρέπει να ερμηνεύσουμε δεδομένα όταν δουλεύουμε με πολλαπλές κατανομές.

Γενικά, τα τρία είδη ευθυγραμμίζονται χαλαρά όσον αφορά τη δημοτικότητα και τη χορευτικότητα. Ο προσδιορισμός clusters σε αυτά τα χαλαρά ευθυγραμμισμένα δεδομένα θα είναι μια πρόκληση:
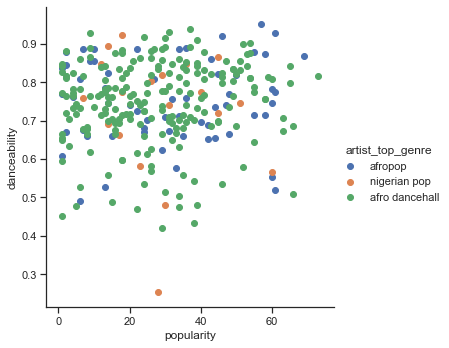
Δημιουργήστε ένα scatter plot:
```
sns.FacetGrid(df, hue="artist_top_genre", height=5) \
   .map(plt.scatter, "popularity", "danceability") \
   .add_legend()
```
Ένα scatterplot των ίδιων αξόνων δείχνει ένα παρόμοιο μοτίβο σύγκλισης

Γενικά, για το clustering, μπορείτε να χρησιμοποιήσετε scatterplots για να δείξετε clusters δεδομένων, οπότε η εξοικείωση με αυτόν τον τύπο οπτικοποίησης είναι πολύ χρήσιμη. Στο επόμενο μάθημα, θα πάρουμε αυτά τα φιλτραρισμένα δεδομένα και θα χρησιμοποιήσουμε το k-means clustering για να ανακαλύψουμε ομάδες σε αυτά τα δεδομένα που φαίνεται να επικαλύπτονται με ενδιαφέροντες τρόπους.

🚀Πρόκληση

Στο πλαίσιο της προετοιμασίας για το επόμενο μάθημα, δημιουργήστε ένα διάγραμμα σχετικά με τους διάφορους αλγόριθμους clustering που μπορεί να ανακαλύψετε και να χρησιμοποιήσετε σε ένα παραγωγικό περιβάλλον. Τι είδους προβλήματα προσπαθεί να αντιμετωπίσει το clustering;

Κουίζ μετά το μάθημα

Ανασκόπηση & Αυτομελέτη

Πριν εφαρμόσετε αλγόριθμους clustering, όπως έχουμε μάθει, είναι καλή ιδέα να κατανοήσετε τη φύση του dataset σας. Διαβάστε περισσότερα για αυτό το θέμα εδώ

Αυτό το χρήσιμο άρθρο σας καθοδηγεί στους διαφορετικούς τρόπους με τους οποίους διάφοροι αλγόριθμοι clustering συμπεριφέρονται, δεδομένων διαφορετικών σχημάτων δεδομένων.

Εργασία

Ερευνήστε άλλες οπτικοποιήσεις για το clustering

Αποποίηση ευθύνης:
Αυτό το έγγραφο έχει μεταφραστεί χρησιμοποιώντας την υπηρεσία αυτόματης μετάφρασης Co-op Translator. Παρόλο που καταβάλλουμε προσπάθειες για ακρίβεια, παρακαλούμε να έχετε υπόψη ότι οι αυτοματοποιημένες μεταφράσεις ενδέχεται να περιέχουν λάθη ή ανακρίβειες. Το πρωτότυπο έγγραφο στη μητρική του γλώσσα θα πρέπει να θεωρείται η αυθεντική πηγή. Για κρίσιμες πληροφορίες, συνιστάται επαγγελματική ανθρώπινη μετάφραση. Δεν φέρουμε ευθύνη για τυχόν παρεξηγήσεις ή εσφαλμένες ερμηνείες που προκύπτουν από τη χρήση αυτής της μετάφρασης.

36 KiB Raw Permalink Blame History Unescape Escape