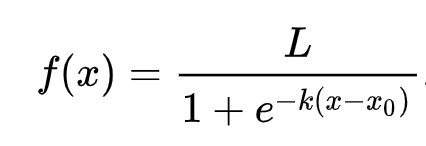31 KiB

Raw Permalink Blame History Unescape Escape

Λογιστική παλινδρόμηση για πρόβλεψη κατηγοριών

Προ-μάθημα κουίζ

Αυτό το μάθημα είναι διαθέσιμο και σε R!

Εισαγωγή

Στο τελευταίο μάθημα για την Παλινδρόμηση, μία από τις βασικές κλασικές τεχνικές Μηχανικής Μάθησης, θα εξετάσουμε τη Λογιστική Παλινδρόμηση. Αυτή η τεχνική χρησιμοποιείται για την ανακάλυψη μοτίβων που προβλέπουν δυαδικές κατηγορίες. Είναι αυτό το γλυκό σοκολάτα ή όχι; Είναι αυτή η ασθένεια μεταδοτική ή όχι; Θα επιλέξει αυτός ο πελάτης το προϊόν ή όχι;

Σε αυτό το μάθημα θα μάθετε:

Μια νέα βιβλιοθήκη για την οπτικοποίηση δεδομένων
Τεχνικές για λογιστική παλινδρόμηση

✅ Εμβαθύνετε την κατανόησή σας για την εργασία με αυτόν τον τύπο παλινδρόμησης σε αυτό το Learn module

Προαπαιτούμενα

Έχοντας δουλέψει με τα δεδομένα κολοκύθας, είμαστε πλέον αρκετά εξοικειωμένοι ώστε να συνειδητοποιήσουμε ότι υπάρχει μία δυαδική κατηγορία με την οποία μπορούμε να δουλέψουμε: Χρώμα.

Ας δημιουργήσουμε ένα μοντέλο λογιστικής παλινδρόμησης για να προβλέψουμε, δεδομένων κάποιων μεταβλητών, ποιο χρώμα είναι πιθανό να έχει μια δεδομένη κολοκύθα (πορτοκαλί 🎃 ή λευκό 👻).

Γιατί μιλάμε για δυαδική ταξινόμηση σε ένα μάθημα που αφορά την παλινδρόμηση; Μόνο για γλωσσική ευκολία, καθώς η λογιστική παλινδρόμηση είναι στην πραγματικότητα μια μέθοδος ταξινόμησης, αν και βασίζεται στη γραμμική παλινδρόμηση. Μάθετε για άλλους τρόπους ταξινόμησης δεδομένων στην επόμενη ομάδα μαθημάτων.

Ορισμός της ερώτησης

Για τους σκοπούς μας, θα εκφράσουμε αυτό ως δυαδικό: 'Λευκό' ή 'Όχι Λευκό'. Υπάρχει επίσης μια κατηγορία 'ριγέ' στο σύνολο δεδομένων μας, αλλά υπάρχουν λίγες περιπτώσεις αυτής, οπότε δεν θα τη χρησιμοποιήσουμε. Εξαφανίζεται ούτως ή άλλως μόλις αφαιρέσουμε τις κενές τιμές από το σύνολο δεδομένων.

🎃 Διασκεδαστικό γεγονός: Μερικές φορές αποκαλούμε τις λευκές κολοκύθες 'κολοκύθες-φαντάσματα'. Δεν είναι πολύ εύκολο να τις σκαλίσουμε, οπότε δεν είναι τόσο δημοφιλείς όσο οι πορτοκαλί, αλλά είναι εντυπωσιακές! Έτσι, θα μπορούσαμε επίσης να διατυπώσουμε την ερώτηση ως: 'Φάντασμα' ή 'Όχι Φάντασμα'. 👻

Σχετικά με τη λογιστική παλινδρόμηση

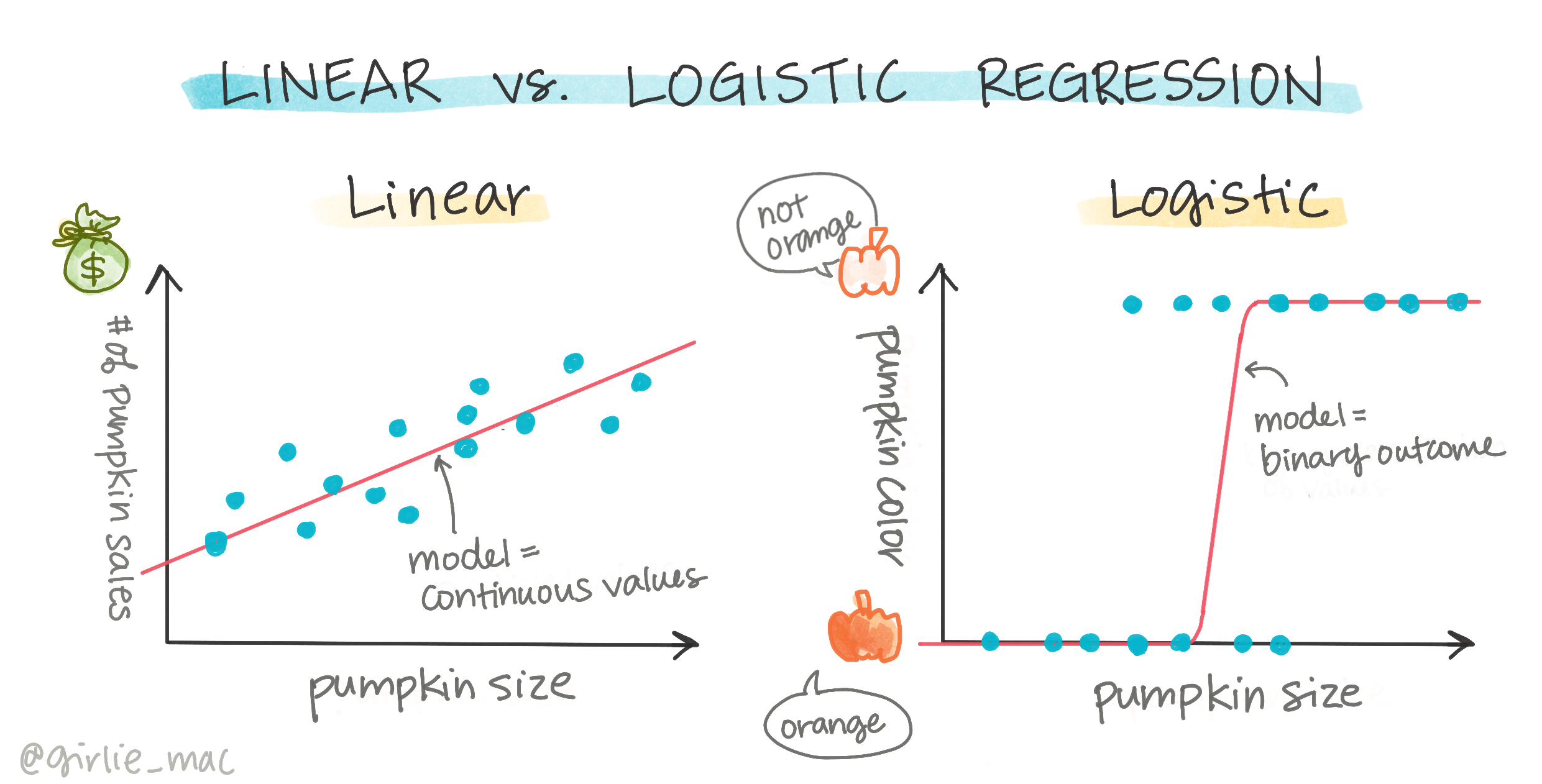
Η λογιστική παλινδρόμηση διαφέρει από τη γραμμική παλινδρόμηση, την οποία μάθατε προηγουμένως, σε μερικούς σημαντικούς τρόπους.

🎥 Κάντε κλικ στην εικόνα παραπάνω για μια σύντομη επισκόπηση της λογιστικής παλινδρόμησης.

Δυαδική ταξινόμηση

Η λογιστική παλινδρόμηση δεν προσφέρει τις ίδιες δυνατότητες με τη γραμμική παλινδρόμηση. Η πρώτη προσφέρει πρόβλεψη για μια δυαδική κατηγορία ("λευκό ή όχι λευκό"), ενώ η δεύτερη είναι ικανή να προβλέπει συνεχείς τιμές, για παράδειγμα, δεδομένης της προέλευσης μιας κολοκύθας και του χρόνου συγκομιδής, πόσο θα αυξηθεί η τιμή της.

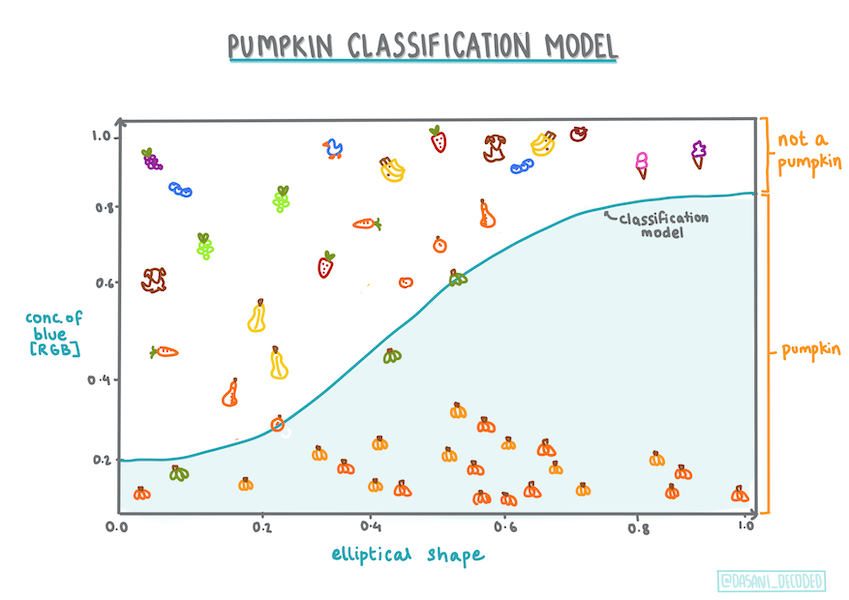
Εικόνα από Dasani Madipalli

Άλλες ταξινομήσεις

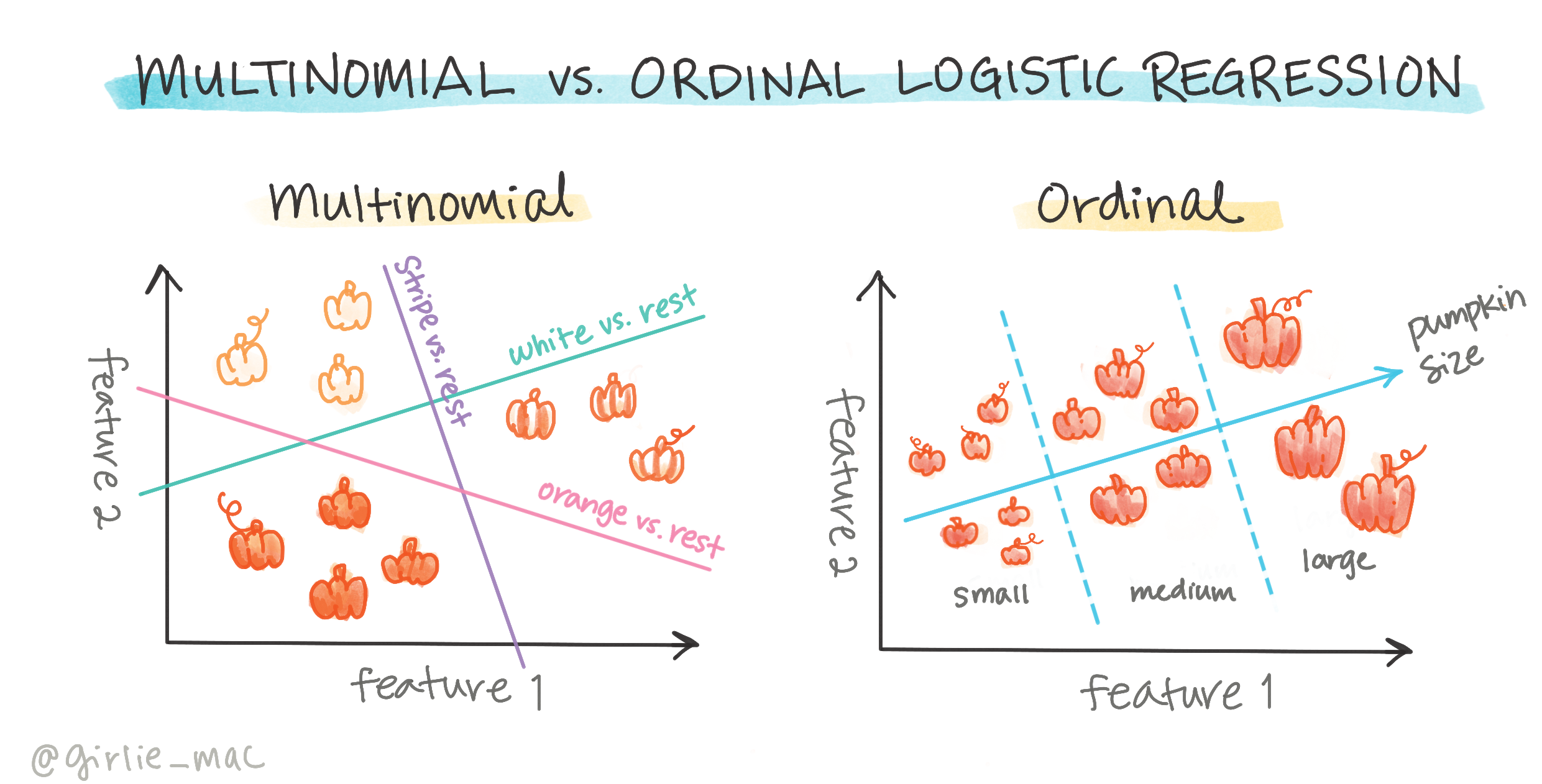
Υπάρχουν άλλοι τύποι λογιστικής παλινδρόμησης, όπως πολυωνυμική και διατακτική:

Πολυωνυμική, που περιλαμβάνει περισσότερες από μία κατηγορίες - "Πορτοκαλί, Λευκό και Ριγέ".
Διατακτική, που περιλαμβάνει διατεταγμένες κατηγορίες, χρήσιμη αν θέλαμε να ταξινομήσουμε τα αποτελέσματά μας λογικά, όπως οι κολοκύθες μας που ταξινομούνται με βάση έναν πεπερασμένο αριθμό μεγεθών (mini, sm, med, lg, xl, xxl).

Οι μεταβλητές ΔΕΝ χρειάζεται να συσχετίζονται

Θυμάστε πώς η γραμμική παλινδρόμηση λειτουργούσε καλύτερα με πιο συσχετισμένες μεταβλητές; Η λογιστική παλινδρόμηση είναι το αντίθετο - οι μεταβλητές δεν χρειάζεται να ευθυγραμμίζονται. Αυτό λειτουργεί για αυτά τα δεδομένα που έχουν σχετικά αδύναμες συσχετίσεις.

Χρειάζεστε πολλά καθαρά δεδομένα

Η λογιστική παλινδρόμηση θα δώσει πιο ακριβή αποτελέσματα αν χρησιμοποιήσετε περισσότερα δεδομένα. Το μικρό μας σύνολο δεδομένων δεν είναι ιδανικό για αυτήν την εργασία, οπότε λάβετε το υπόψη σας.

🎥 Κάντε κλικ στην εικόνα παραπάνω για μια σύντομη επισκόπηση της προετοιμασίας δεδομένων για γραμμική παλινδρόμηση

✅ Σκεφτείτε τους τύπους δεδομένων που θα μπορούσαν να ταιριάζουν καλά στη λογιστική παλινδρόμηση

Άσκηση - καθαρισμός δεδομένων

Πρώτα, καθαρίστε λίγο τα δεδομένα, αφαιρώντας τις κενές τιμές και επιλέγοντας μόνο ορισμένες στήλες:

Προσθέστε τον παρακάτω κώδικα:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Μπορείτε πάντα να ρίξετε μια ματιά στο νέο σας dataframe:

pumpkins.info

Οπτικοποίηση - κατηγορικό διάγραμμα

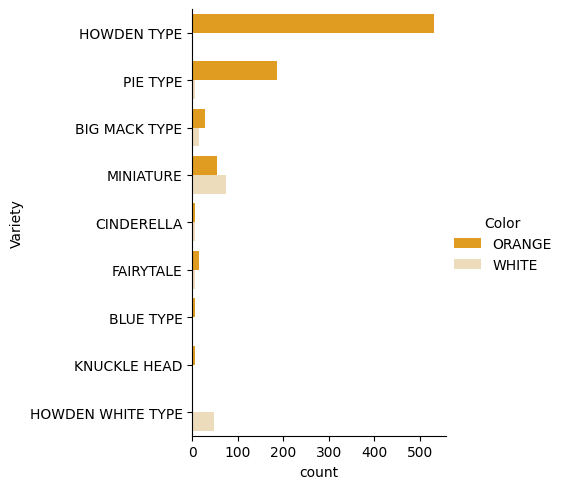
Μέχρι τώρα έχετε φορτώσει το αρχικό notebook με δεδομένα κολοκύθας ξανά και το έχετε καθαρίσει ώστε να διατηρεί ένα σύνολο δεδομένων που περιέχει μερικές μεταβλητές, συμπεριλαμβανομένου του Χρώματος. Ας οπτικοποιήσουμε το dataframe στο notebook χρησιμοποιώντας μια διαφορετική βιβλιοθήκη: Seaborn, η οποία βασίζεται στο Matplotlib που χρησιμοποιήσαμε νωρίτερα.

Το Seaborn προσφέρει μερικούς έξυπνους τρόπους για να οπτικοποιήσετε τα δεδομένα σας. Για παράδειγμα, μπορείτε να συγκρίνετε τις κατανομές των δεδομένων για κάθε Ποικιλία και Χρώμα σε ένα κατηγορικό διάγραμμα.

Δημιουργήστε ένα τέτοιο διάγραμμα χρησιμοποιώντας τη συνάρτηση catplot, χρησιμοποιώντας τα δεδομένα κολοκύθας pumpkins και καθορίζοντας έναν χρωματικό χάρτη για κάθε κατηγορία κολοκύθας (πορτοκαλί ή λευκό):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Παρατηρώντας τα δεδομένα, μπορείτε να δείτε πώς τα δεδομένα Χρώματος σχετίζονται με την Ποικιλία.

✅ Δεδομένου αυτού του κατηγορικού διαγράμματος, ποιες ενδιαφέρουσες εξερευνήσεις μπορείτε να φανταστείτε;

Προεπεξεργασία δεδομένων: κωδικοποίηση χαρακτηριστικών και ετικετών

Το σύνολο δεδομένων κολοκύθας μας περιέχει τιμές κειμένου για όλες τις στήλες του. Η εργασία με κατηγορικά δεδομένα είναι διαισθητική για τους ανθρώπους αλλά όχι για τις μηχανές. Οι αλγόριθμοι μηχανικής μάθησης λειτουργούν καλά με αριθμούς. Γι' αυτό η κωδικοποίηση είναι ένα πολύ σημαντικό βήμα στη φάση προεπεξεργασίας δεδομένων, καθώς μας επιτρέπει να μετατρέψουμε τα κατηγορικά δεδομένα σε αριθμητικά δεδομένα, χωρίς να χάσουμε καμία πληροφορία. Καλή κωδικοποίηση οδηγεί στη δημιουργία ενός καλού μοντέλου.

Για την κωδικοποίηση χαρακτηριστικών υπάρχουν δύο κύριοι τύποι κωδικοποιητών:

Ordinal encoder: ταιριάζει καλά για διατακτικές μεταβλητές, οι οποίες είναι κατηγορικές μεταβλητές όπου τα δεδομένα τους ακολουθούν μια λογική σειρά, όπως η στήλη Item Size στο σύνολο δεδομένων μας. Δημιουργεί έναν χάρτη έτσι ώστε κάθε κατηγορία να αντιπροσωπεύεται από έναν αριθμό, που είναι η σειρά της κατηγορίας στη στήλη.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Categorical encoder: ταιριάζει καλά για ονομαστικές μεταβλητές, οι οποίες είναι κατηγορικές μεταβλητές όπου τα δεδομένα τους δεν ακολουθούν μια λογική σειρά, όπως όλα τα χαρακτηριστικά εκτός από το Item Size στο σύνολο δεδομένων μας. Είναι μια κωδικοποίηση one-hot, που σημαίνει ότι κάθε κατηγορία αντιπροσωπεύεται από μια δυαδική στήλη: η κωδικοποιημένη μεταβλητή είναι ίση με 1 αν η κολοκύθα ανήκει σε αυτήν την Ποικιλία και 0 διαφορετικά.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Στη συνέχεια, χρησιμοποιείται το ColumnTransformer για να συνδυάσει πολλούς κωδικοποιητές σε ένα βήμα και να τους εφαρμόσει στις κατάλληλες στήλες.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Από την άλλη πλευρά, για την κωδικοποίηση της ετικέτας, χρησιμοποιούμε την κλάση LabelEncoder της scikit-learn, η οποία είναι μια βοηθητική κλάση για την κανονικοποίηση ετικετών ώστε να περιέχουν μόνο τιμές μεταξύ 0 και n_classes-1 (εδώ, 0 και 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Μόλις κωδικοποιήσουμε τα χαρακτηριστικά και την ετικέτα, μπορούμε να τα συγχωνεύσουμε σε ένα νέο dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Ποια είναι τα πλεονεκτήματα της χρήσης ενός ordinal encoder για τη στήλη Item Size;

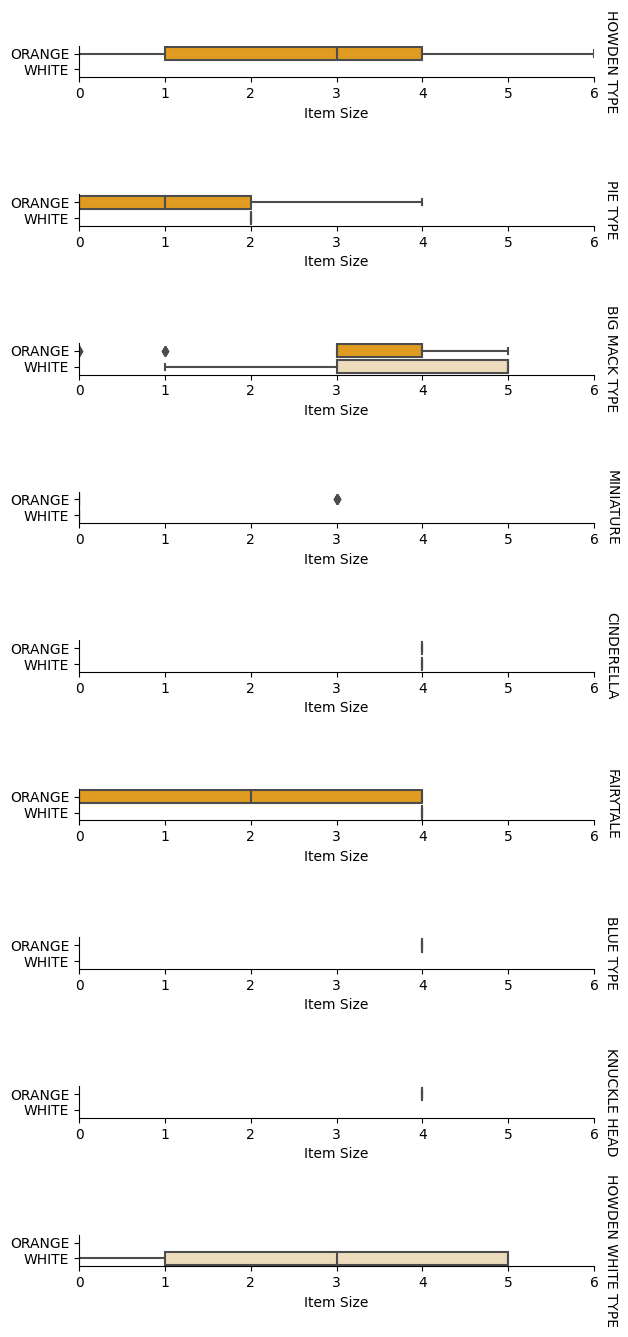
Ανάλυση σχέσεων μεταξύ μεταβλητών

Τώρα που έχουμε προεπεξεργαστεί τα δεδομένα μας, μπορούμε να αναλύσουμε τις σχέσεις μεταξύ των χαρακτηριστικών και της ετικέτας για να αποκτήσουμε μια ιδέα για το πόσο καλά το μοντέλο θα μπορέσει να προβλέψει την ετικέτα δεδομένων των χαρακτηριστικών.

Ο καλύτερος τρόπος για να πραγματοποιήσουμε αυτό το είδος ανάλυσης είναι να σχεδιάσουμε τα δεδομένα. Θα χρησιμοποιήσουμε ξανά τη συνάρτηση catplot του Seaborn, για να οπτικοποιήσουμε τις σχέσεις μεταξύ Item Size, Variety και Color σε ένα κατηγορικό διάγραμμα. Για καλύτερη απεικόνιση των δεδομένων θα χρησιμοποιήσουμε την κωδικοποιημένη στήλη Item Size και την μη κωδικοποιημένη στήλη Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

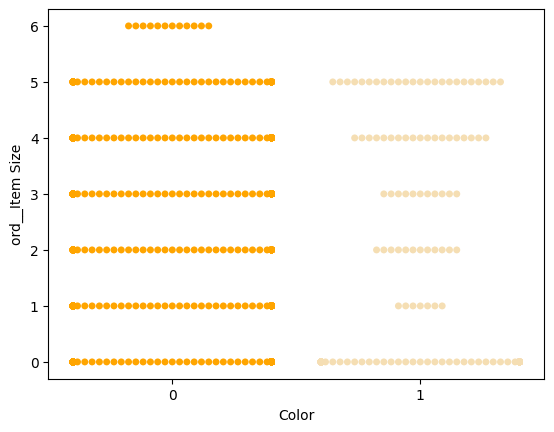
Χρήση swarm plot

Επειδή το Χρώμα είναι μια δυαδική κατηγορία (Λευκό ή Όχι), χρειάζεται 'μια εξειδικευμένη προσέγγιση για την οπτικοποίηση'. Υπάρχουν άλλοι τρόποι για να οπτικοποιήσετε τη σχέση αυτής της κατηγορίας με άλλες μεταβλητές.

Μπορείτε να οπτικοποιήσετε μεταβλητές δίπλα-δίπλα με διαγράμματα Seaborn.

Δοκιμάστε ένα διάγραμμα 'swarm' για να δείξετε την κατανομή των τιμών:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Προσοχή: ο παραπάνω κώδικας μπορεί να δημιουργήσει μια προειδοποίηση, καθώς το seaborn αποτυγχάνει να αναπαραστήσει τέτοιο αριθμό σημείων δεδομένων σε ένα swarm plot. Μια πιθανή λύση είναι η μείωση του μεγέθους του δείκτη, χρησιμοποιώντας την παράμετρο 'size'. Ωστόσο, να είστε προσεκτικοί καθώς αυτό επηρεάζει την αναγνωσιμότητα του διαγράμματος.

🧮 Δείξτε μου τα Μαθηματικά

Η λογιστική παλινδρόμηση βασίζεται στην έννοια της 'μέγιστης πιθανότητας' χρησιμοποιώντας συναρτήσεις sigmoid. Μια 'Συνάρτηση Sigmoid' σε ένα διάγραμμα μοιάζει με σχήμα 'S'. Παίρνει μια τιμή και τη χαρτογραφεί κάπου μεταξύ 0 και 1. Η καμπύλη της ονομάζεται επίσης 'λογιστική καμπύλη'. Ο τύπος της μοιάζει με αυτόν:

όπου το μέσο της sigmoid βρίσκεται στο σημείο 0 του x, το L είναι η μέγιστη τιμή της καμπύλης και το k είναι η απότομη κλίση της καμπύλης. Αν το αποτέλεσμα της συνάρτησης είναι μεγαλύτερο από 0.5, η ετικέτα θα λάβει την κατηγορία '1' της δυαδικής επιλογής. Αν όχι, θα ταξινομηθεί ως '0'.

Δημιουργία του μοντέλου σας

Η δημιουργία ενός μοντέλου για την εύρεση αυτών των δυαδικών ταξινομήσεων είναι εκπληκτικά απλή στο Scikit-learn.

🎥 Κάντε κλικ στην εικόνα παραπάνω για μια σύντομη επισκόπηση της δημιουργίας ενός μοντέλου γραμμικής παλινδρόμησης

Επιλέξτε τις μεταβλητές που θέλετε να χρησιμοποιήσετε στο μοντέλο ταξινόμησης και χωρίστε τα σύνολα εκπαίδευσης και δοκιμής καλώντας τη συνάρτηση train_test_split():
```
from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
Τώρα μπορείτε να εκπαιδεύσετε το μοντέλο σας, καλώντας τη συνάρτηση fit() με τα Πώς σχετίζεται ο πίνακας σύγχυσης με την ακρίβεια και την ανάκληση; Θυμηθείτε, η αναφορά ταξινόμησης που εκτυπώθηκε παραπάνω έδειξε ακρίβεια (0.85) και ανάκληση (0.67).

Ακρίβεια = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Ανάκληση = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ Ε: Σύμφωνα με τον πίνακα σύγχυσης, πώς τα πήγε το μοντέλο; Α: Όχι άσχημα· υπάρχουν αρκετά σωστά αρνητικά αλλά και μερικά ψευδώς αρνητικά.

Ας επανεξετάσουμε τους όρους που είδαμε νωρίτερα με τη βοήθεια της αντιστοίχισης TP/TN και FP/FN του πίνακα σύγχυσης:

🎓 Ακρίβεια: TP/(TP + FP) Το ποσοστό των σχετικών περιπτώσεων μεταξύ των ανακτημένων περιπτώσεων (π.χ. ποιες ετικέτες ήταν σωστά επισημασμένες)

🎓 Ανάκληση: TP/(TP + FN) Το ποσοστό των σχετικών περιπτώσεων που ανακτήθηκαν, είτε ήταν σωστά επισημασμένες είτε όχι

🎓 f1-score: (2 * ακρίβεια * ανάκληση)/(ακρίβεια + ανάκληση) Ένας σταθμισμένος μέσος όρος της ακρίβειας και της ανάκλησης, με το καλύτερο να είναι 1 και το χειρότερο να είναι 0

🎓 Υποστήριξη: Ο αριθμός των εμφανίσεων κάθε ετικέτας που ανακτήθηκε

🎓 Ακρίβεια: (TP + TN)/(TP + TN + FP + FN) Το ποσοστό των ετικετών που προβλέφθηκαν σωστά για ένα δείγμα.

🎓 Μακρο Μέσος Όρος: Ο υπολογισμός του μη σταθμισμένου μέσου όρου των μετρικών για κάθε ετικέτα, χωρίς να λαμβάνεται υπόψη η ανισορροπία των ετικετών.

🎓 Σταθμισμένος Μέσος Όρος: Ο υπολογισμός του μέσου όρου των μετρικών για κάθε ετικέτα, λαμβάνοντας υπόψη την ανισορροπία των ετικετών με τη στάθμιση τους βάσει της υποστήριξής τους (ο αριθμός των πραγματικών περιπτώσεων για κάθε ετικέτα).

✅ Μπορείτε να σκεφτείτε ποια μετρική πρέπει να παρακολουθείτε αν θέλετε το μοντέλο σας να μειώσει τον αριθμό των ψευδώς αρνητικών;

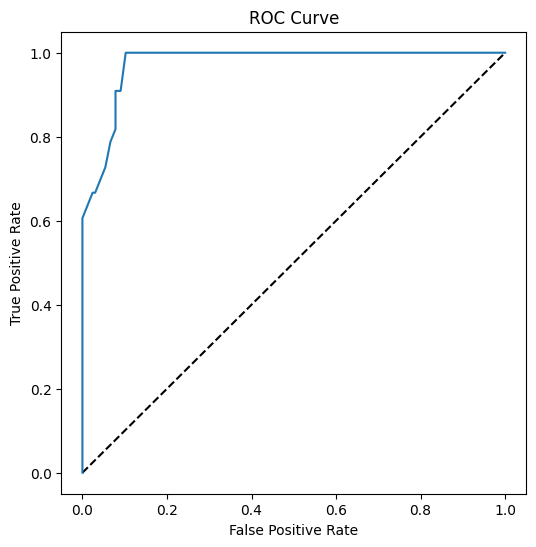
Οπτικοποίηση της καμπύλης ROC αυτού του μοντέλου

🎥 Κάντε κλικ στην εικόνα παραπάνω για ένα σύντομο βίντεο επισκόπησης των καμπυλών ROC

Ας κάνουμε μία ακόμη οπτικοποίηση για να δούμε τη λεγόμενη 'καμπύλη ROC':

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Χρησιμοποιώντας το Matplotlib, σχεδιάστε την Καμπύλη Λειτουργίας Λήψης ή ROC του μοντέλου. Οι καμπύλες ROC χρησιμοποιούνται συχνά για να αποκτήσετε μια εικόνα της εξόδου ενός ταξινομητή όσον αφορά τα σωστά έναντι των ψευδώς θετικών. "Οι καμπύλες ROC συνήθως εμφανίζουν το ποσοστό σωστών θετικών στον άξονα Y και το ποσοστό ψευδώς θετικών στον άξονα X." Έτσι, η απότομη κλίση της καμπύλης και ο χώρος μεταξύ της γραμμής του μέσου σημείου και της καμπύλης έχουν σημασία: θέλετε μια καμπύλη που γρήγορα ανεβαίνει και ξεπερνά τη γραμμή. Στην περίπτωσή μας, υπάρχουν ψευδώς θετικά στην αρχή, και στη συνέχεια η γραμμή ανεβαίνει και ξεπερνά σωστά:

Τέλος, χρησιμοποιήστε το API roc_auc_score του Scikit-learn για να υπολογίσετε την πραγματική 'Περιοχή Κάτω από την Καμπύλη' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Το αποτέλεσμα είναι 0.9749908725812341. Δεδομένου ότι το AUC κυμαίνεται από 0 έως 1, θέλετε ένα μεγάλο σκορ, καθώς ένα μοντέλο που είναι 100% σωστό στις προβλέψεις του θα έχει AUC ίσο με 1· σε αυτή την περίπτωση, το μοντέλο είναι αρκετά καλό.

Στα μελλοντικά μαθήματα για ταξινομήσεις, θα μάθετε πώς να επαναλαμβάνετε για να βελτιώσετε τα σκορ του μοντέλου σας. Αλλά προς το παρόν, συγχαρητήρια! Ολοκληρώσατε αυτά τα μαθήματα για την παλινδρόμηση!

🚀Πρόκληση

Υπάρχουν πολλά περισσότερα να εξερευνήσετε σχετικά με τη λογιστική παλινδρόμηση! Αλλά ο καλύτερος τρόπος για να μάθετε είναι να πειραματιστείτε. Βρείτε ένα σύνολο δεδομένων που ταιριάζει σε αυτόν τον τύπο ανάλυσης και δημιουργήστε ένα μοντέλο με αυτό. Τι μαθαίνετε; συμβουλή: δοκιμάστε το Kaggle για ενδιαφέροντα σύνολα δεδομένων.

Κουίζ μετά το μάθημα

Ανασκόπηση & Αυτομελέτη

Διαβάστε τις πρώτες σελίδες αυτής της εργασίας από το Stanford σχετικά με κάποιες πρακτικές χρήσεις της λογιστικής παλινδρόμησης. Σκεφτείτε εργασίες που είναι καλύτερα προσαρμοσμένες για έναν ή τον άλλο τύπο παλινδρομήσεων που έχουμε μελετήσει μέχρι τώρα. Τι θα λειτουργούσε καλύτερα;

Εργασία

Επαναπροσπάθεια αυτής της παλινδρόμησης

Αποποίηση ευθύνης:
Αυτό το έγγραφο έχει μεταφραστεί χρησιμοποιώντας την υπηρεσία αυτόματης μετάφρασης Co-op Translator. Παρόλο που καταβάλλουμε προσπάθειες για ακρίβεια, παρακαλούμε να έχετε υπόψη ότι οι αυτοματοποιημένες μεταφράσεις ενδέχεται να περιέχουν λάθη ή ανακρίβειες. Το πρωτότυπο έγγραφο στη μητρική του γλώσσα θα πρέπει να θεωρείται η αυθεντική πηγή. Για κρίσιμες πληροφορίες, συνιστάται επαγγελματική ανθρώπινη μετάφραση. Δεν φέρουμε ευθύνη για τυχόν παρεξηγήσεις ή εσφαλμένες ερμηνείες που προκύπτουν από τη χρήση αυτής της μετάφρασης.

31 KiB Raw Permalink Blame History Unescape Escape