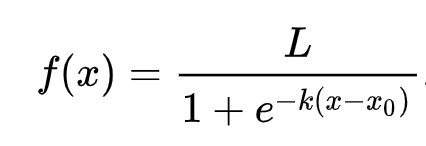24 KiB

Raw Permalink Blame History Unescape Escape

Logistische Regression zur Vorhersage von Kategorien

Quiz vor der Lektion

Diese Lektion ist auch in R verfügbar!

Einführung

In dieser letzten Lektion zur Regression, einer der grundlegenden klassischen ML-Techniken, werfen wir einen Blick auf die logistische Regression. Diese Technik wird verwendet, um Muster zu erkennen und binäre Kategorien vorherzusagen. Ist diese Süßigkeit Schokolade oder nicht? Ist diese Krankheit ansteckend oder nicht? Wird dieser Kunde dieses Produkt wählen oder nicht?

In dieser Lektion lernen Sie:

Eine neue Bibliothek für Datenvisualisierung
Techniken für die logistische Regression

✅ Vertiefen Sie Ihr Verständnis für diese Art der Regression in diesem Learn-Modul

Voraussetzungen

Nachdem wir mit den Kürbisdaten gearbeitet haben, sind wir nun vertraut genug, um zu erkennen, dass es eine binäre Kategorie gibt, mit der wir arbeiten können: Color.

Lassen Sie uns ein Modell der logistischen Regression erstellen, um vorherzusagen, welche Farbe ein gegebener Kürbis wahrscheinlich hat (orange 🎃 oder weiß 👻), basierend auf einigen Variablen.

Warum sprechen wir in einer Lektion über Regression über binäre Klassifikation? Nur aus sprachlicher Bequemlichkeit, da die logistische Regression eigentlich eine Klassifikationsmethode ist, wenn auch eine lineare. Lernen Sie in der nächsten Lektion weitere Methoden zur Klassifikation von Daten kennen.

Die Frage definieren

Für unsere Zwecke formulieren wir dies als Binärfrage: 'Weiß' oder 'Nicht Weiß'. Es gibt auch eine 'gestreifte' Kategorie in unserem Datensatz, aber es gibt nur wenige Instanzen davon, sodass wir sie nicht verwenden. Sie verschwindet ohnehin, sobald wir Nullwerte aus dem Datensatz entfernen.

🎃 Fun Fact: Weiße Kürbisse werden manchmal als 'Geisterkürbisse' bezeichnet. Sie sind nicht sehr leicht zu schnitzen, daher sind sie nicht so beliebt wie die orangefarbenen, aber sie sehen cool aus! Wir könnten unsere Frage also auch so formulieren: 'Geist' oder 'Nicht Geist'. 👻

Über logistische Regression

Die logistische Regression unterscheidet sich in einigen wichtigen Punkten von der linearen Regression, die Sie zuvor kennengelernt haben.

🎥 Klicken Sie auf das Bild oben für eine kurze Videoübersicht zur logistischen Regression.

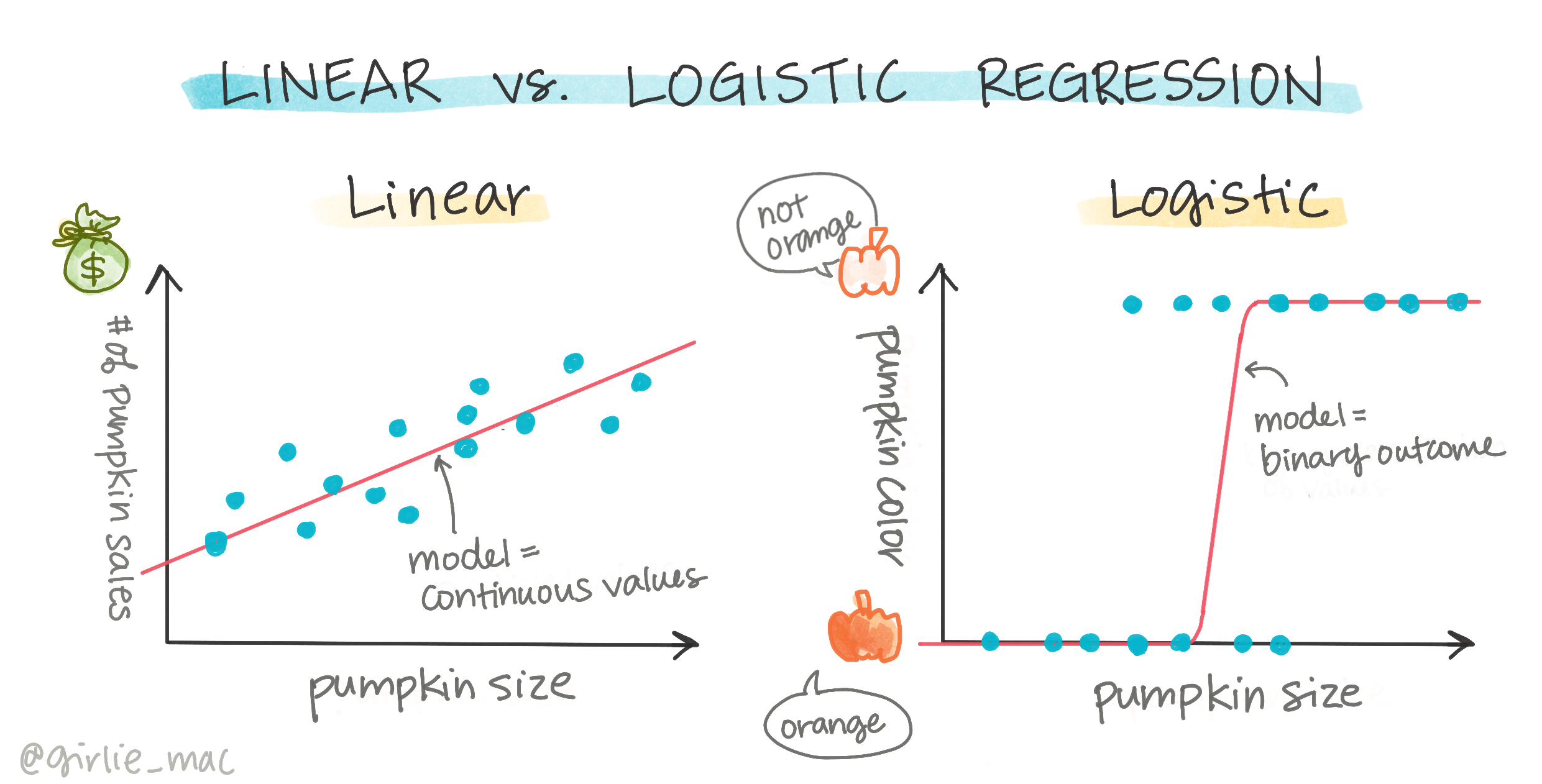
Binäre Klassifikation

Die logistische Regression bietet nicht dieselben Funktionen wie die lineare Regression. Erstere liefert eine Vorhersage über eine binäre Kategorie ("weiß oder nicht weiß"), während letztere kontinuierliche Werte vorhersagen kann, z. B. wie stark der Preis eines Kürbisses basierend auf seinem Ursprung und der Erntezeit steigen wird.

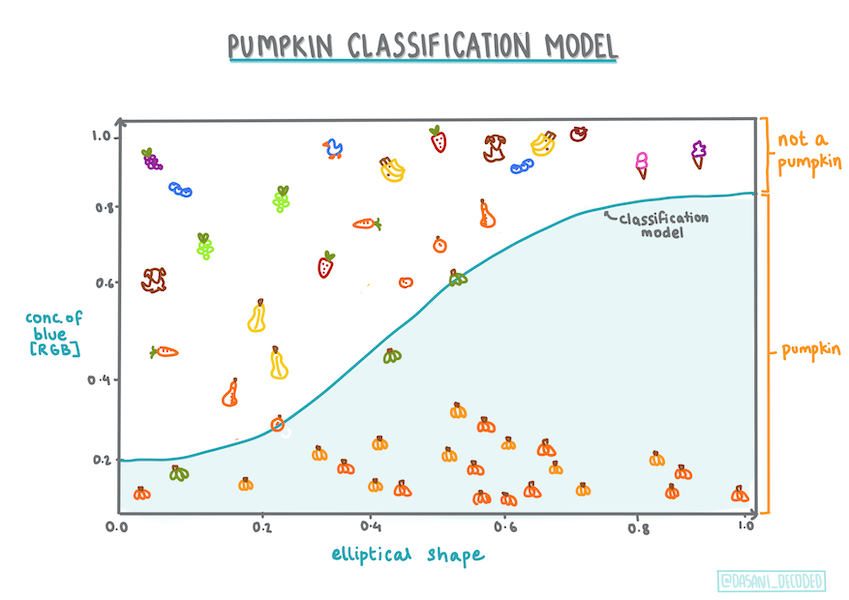
Infografik von Dasani Madipalli

Andere Klassifikationen

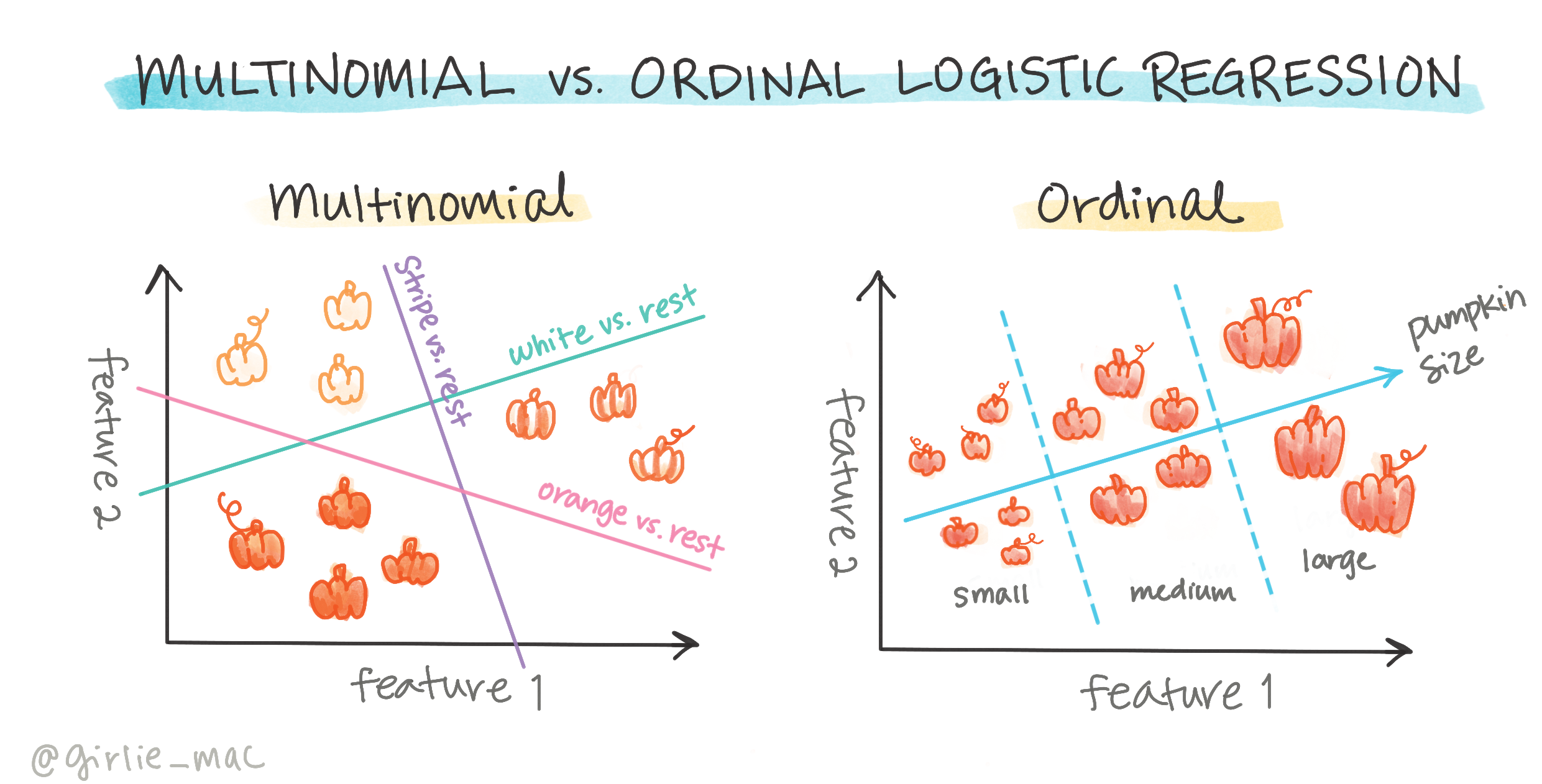
Es gibt andere Arten der logistischen Regression, darunter multinomial und ordinal:

Multinomial, bei der es mehr als eine Kategorie gibt - "Orange, Weiß und Gestreift".
Ordinal, bei der es geordnete Kategorien gibt, nützlich, wenn wir unsere Ergebnisse logisch ordnen möchten, wie z. B. unsere Kürbisse, die nach einer endlichen Anzahl von Größen (mini, sm, med, lg, xl, xxl) geordnet sind.

Variablen MÜSSEN NICHT korrelieren

Erinnern Sie sich, wie die lineare Regression mit stärker korrelierten Variablen besser funktionierte? Bei der logistischen Regression ist das Gegenteil der Fall – die Variablen müssen nicht übereinstimmen. Das funktioniert gut für diese Daten, die nur schwache Korrelationen aufweisen.

Sie benötigen viele saubere Daten

Die logistische Regression liefert genauere Ergebnisse, wenn Sie mehr Daten verwenden; unser kleiner Datensatz ist für diese Aufgabe nicht optimal, also behalten Sie das im Hinterkopf.

🎥 Klicken Sie auf das Bild oben für eine kurze Videoübersicht zur Datenvorbereitung für die lineare Regression.

✅ Überlegen Sie, welche Arten von Daten sich gut für die logistische Regression eignen würden.

Übung - Daten bereinigen

Bereinigen Sie zunächst die Daten ein wenig, indem Sie Nullwerte entfernen und nur einige der Spalten auswählen:

Fügen Sie den folgenden Code hinzu:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Sie können sich jederzeit Ihren neuen DataFrame ansehen:

pumpkins.info

Visualisierung - Kategorisches Diagramm

Bis jetzt haben Sie das Starter-Notebook mit Kürbisdaten geladen und bereinigt, sodass ein Datensatz mit einigen Variablen, einschließlich Color, erhalten bleibt. Lassen Sie uns den DataFrame im Notebook mit einer anderen Bibliothek visualisieren: Seaborn, das auf Matplotlib basiert, das wir zuvor verwendet haben.

Seaborn bietet einige interessante Möglichkeiten, Ihre Daten zu visualisieren. Zum Beispiel können Sie die Verteilungen der Daten für jede Variety und Color in einem kategorischen Diagramm vergleichen.

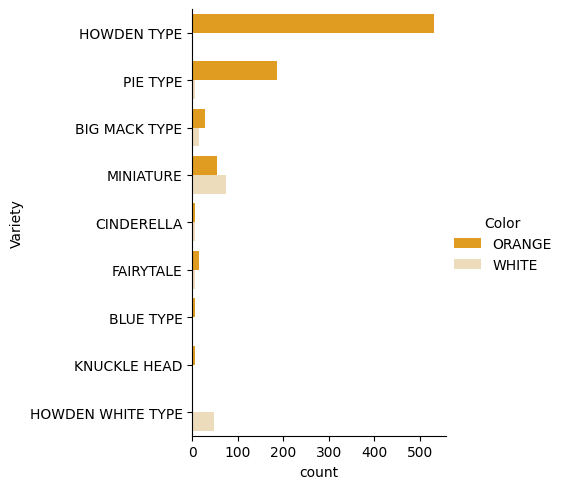
Erstellen Sie ein solches Diagramm mit der Funktion catplot, indem Sie unsere Kürbisdaten pumpkins verwenden und eine Farbzuordnung für jede Kürbiskategorie (orange oder weiß) angeben:
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Durch die Beobachtung der Daten können Sie sehen, wie die Farbdaten mit der Sorte zusammenhängen.

✅ Welche interessanten Untersuchungen können Sie sich anhand dieses kategorischen Diagramms vorstellen?

Datenvorverarbeitung: Feature- und Label-Encoding

Unser Kürbisdatensatz enthält Zeichenkettenwerte für alle Spalten. Mit kategorialen Daten zu arbeiten, ist für Menschen intuitiv, aber nicht für Maschinen. Maschinelle Lernalgorithmen arbeiten gut mit Zahlen. Deshalb ist Encoding ein sehr wichtiger Schritt in der Datenvorverarbeitungsphase, da es uns ermöglicht, kategoriale Daten in numerische Daten umzuwandeln, ohne Informationen zu verlieren. Gutes Encoding führt zu einem guten Modell.

Für das Feature-Encoding gibt es zwei Haupttypen von Encodern:

Ordinal-Encoder: Er eignet sich gut für ordinale Variablen, also kategoriale Variablen, deren Daten einer logischen Reihenfolge folgen, wie die Spalte Item Size in unserem Datensatz. Er erstellt eine Zuordnung, sodass jede Kategorie durch eine Zahl dargestellt wird, die der Reihenfolge der Kategorie in der Spalte entspricht.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorischer Encoder: Er eignet sich gut für nominale Variablen, also kategoriale Variablen, deren Daten keiner logischen Reihenfolge folgen, wie alle Merkmale außer Item Size in unserem Datensatz. Es handelt sich um ein One-Hot-Encoding, was bedeutet, dass jede Kategorie durch eine binäre Spalte dargestellt wird: Die codierte Variable ist gleich 1, wenn der Kürbis zu dieser Sorte gehört, und 0, andernfalls.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Dann wird ColumnTransformer verwendet, um mehrere Encoder in einem einzigen Schritt zu kombinieren und auf die entsprechenden Spalten anzuwenden.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Zum Codieren des Labels verwenden wir die LabelEncoder-Klasse von Scikit-learn, eine Dienstprogrammsklasse, die dabei hilft, Labels zu normalisieren, sodass sie nur Werte zwischen 0 und n_classes-1 (hier 0 und 1) enthalten.

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Sobald wir die Merkmale und das Label codiert haben, können wir sie in einem neuen DataFrame encoded_pumpkins zusammenführen.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Welche Vorteile hat die Verwendung eines Ordinal-Encoders für die Spalte Item Size?

Beziehungen zwischen Variablen analysieren

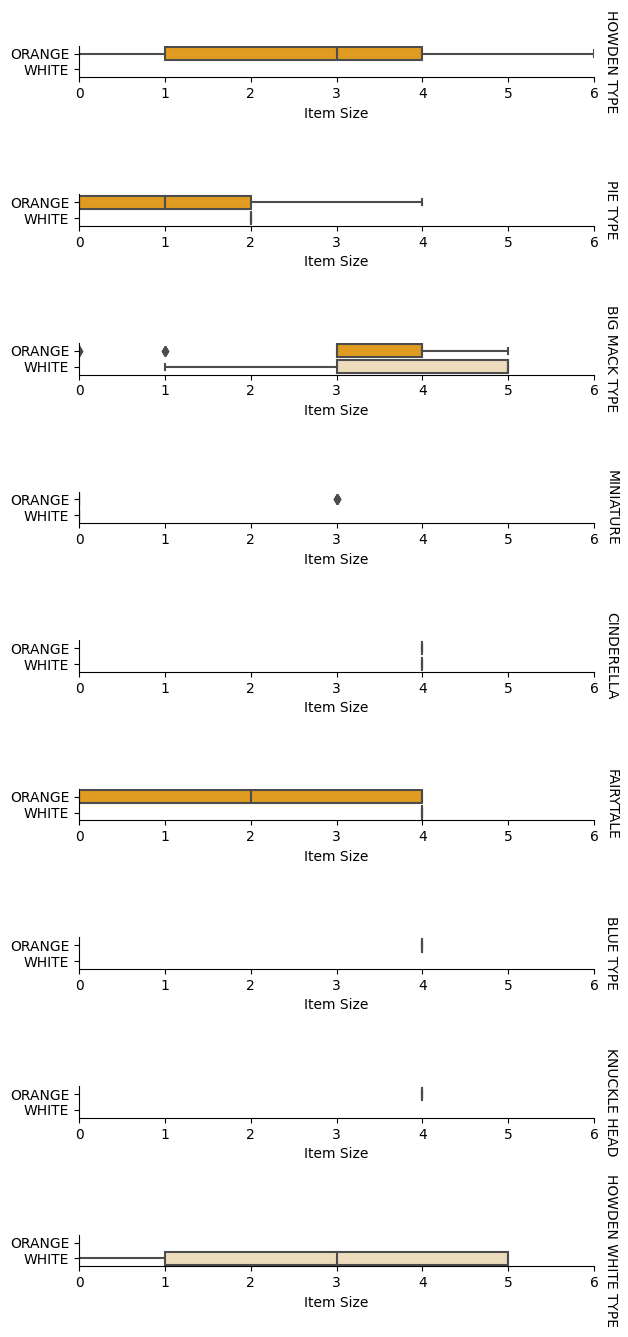
Nachdem wir unsere Daten vorverarbeitet haben, können wir die Beziehungen zwischen den Merkmalen und dem Label analysieren, um eine Vorstellung davon zu bekommen, wie gut das Modell das Label anhand der Merkmale vorhersagen kann. Die beste Möglichkeit, diese Art von Analyse durchzuführen, ist das Plotten der Daten. Wir verwenden erneut die Seaborn-Funktion catplot, um die Beziehungen zwischen Item Size, Variety und Color in einem kategorischen Diagramm zu visualisieren. Um die Daten besser darzustellen, verwenden wir die codierte Spalte Item Size und die nicht codierte Spalte Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Verwenden Sie einen Swarm-Plot

Da Color eine binäre Kategorie (Weiß oder Nicht Weiß) ist, benötigt sie 'einen spezialisierten Ansatz zur Visualisierung'. Es gibt andere Möglichkeiten, die Beziehung dieser Kategorie zu anderen Variablen zu visualisieren.

Sie können Variablen nebeneinander mit Seaborn-Diagrammen visualisieren.

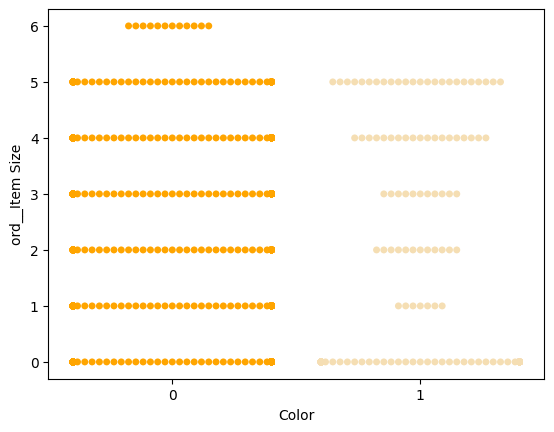
Probieren Sie einen 'Swarm'-Plot aus, um die Verteilung der Werte darzustellen:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Achtung: Der obige Code könnte eine Warnung generieren, da Seaborn Schwierigkeiten hat, eine solche Menge an Datenpunkten in einem Swarm-Plot darzustellen. Eine mögliche Lösung ist, die Größe der Marker mit dem Parameter 'size' zu verringern. Beachten Sie jedoch, dass dies die Lesbarkeit des Diagramms beeinträchtigen kann.

🧮 Zeigen Sie mir die Mathematik

Die logistische Regression basiert auf dem Konzept der 'Maximum-Likelihood' unter Verwendung von Sigmoid-Funktionen. Eine 'Sigmoid-Funktion' sieht auf einem Diagramm wie eine 'S'-Form aus. Sie nimmt einen Wert und ordnet ihn einem Bereich zwischen 0 und 1 zu. Ihre Kurve wird auch als 'logistische Kurve' bezeichnet. Ihre Formel sieht so aus:

Dabei liegt der Mittelpunkt der Sigmoid-Funktion bei x = 0, L ist der maximale Wert der Kurve, und k ist die Steilheit der Kurve. Wenn das Ergebnis der Funktion größer als 0,5 ist, wird das Label der Klasse '1' der binären Wahl zugeordnet. Andernfalls wird es als '0' klassifiziert.

Erstellen Sie Ihr Modell

Ein Modell zu erstellen, um diese binäre Klassifikation zu finden, ist in Scikit-learn überraschend einfach.

🎥 Klicken Sie auf das Bild oben für eine kurze Videoübersicht zum Erstellen eines linearen Regressionsmodells.

Wählen Sie die Variablen aus, die Sie in Ihrem Klassifikationsmodell verwenden möchten, und teilen Sie die Trainings- und Testdatensätze mit train_test_split() auf:

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Jetzt können Sie Ihr Modell trainieren, indem Sie fit() mit Ihren Trainingsdaten aufrufen, und das Ergebnis ausgeben:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Werfen Sie einen Blick auf die Bewertung Ihres Modells. Es ist nicht schlecht, wenn man bedenkt, dass Sie nur etwa 1000 Datenzeilen haben:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Bessere Verständlichkeit durch eine Konfusionsmatrix

Während Sie einen Bewertungsbericht Begriffe durch die oben genannten Elemente ausgeben können, könnten Sie Ihr Modell leichter verstehen, indem Sie eine Konfusionsmatrix verwenden, um zu analysieren, wie das Modell abschneidet.

🎓 Eine 'Konfusionsmatrix' (oder 'Fehlermatrix') ist eine Tabelle, die die tatsächlichen vs. vorhergesagten positiven und negativen Werte Ihres Modells darstellt und so die Genauigkeit der Vorhersagen misst.

Um eine Konfusionsmatrix zu verwenden, rufen Sie confusion_matrix() auf:
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)
```
Werfen Sie einen Blick auf die Konfusionsmatrix Ihres Modells:
```
array([[162,   4],
       [ 11,  22]])
```

In Scikit-learn sind die Zeilen (Achse 0) die tatsächlichen Labels und die Spalten (Achse 1) die vorhergesagten Labels.

	0	1
0	TN	FP
1	FN	TP

Was passiert hier? Angenommen, unser Modell soll Kürbisse zwischen zwei binären Kategorien klassifizieren: Kategorie 'weiß' und Kategorie 'nicht-weiß'.

Wenn Ihr Modell einen Kürbis als nicht weiß vorhersagt und er tatsächlich zur Kategorie 'nicht-weiß' gehört, nennen wir das ein True Negative (TN), dargestellt durch die Zahl oben links.
Wenn Ihr Modell einen Kürbis als weiß vorhersagt und er tatsächlich zur Kategorie 'nicht-weiß' gehört, nennen wir das ein False Negative (FN), dargestellt durch die Zahl unten links.
Wenn Ihr Modell einen Kürbis als nicht weiß vorhersagt und er tatsächlich zur Kategorie 'weiß' gehört, nennen wir das ein False Positive (FP), dargestellt durch die Zahl oben rechts.
Wenn Ihr Modell einen Kürbis als weiß vorhersagt und er tatsächlich zur Kategorie 'weiß' gehört, nennen wir das ein True Positive (TP), dargestellt durch die Zahl unten rechts.

Wie Sie sich denken können, ist es wünschenswert, eine größere Anzahl von True Positives und True Negatives sowie eine geringere Anzahl von False Positives und False Negatives zu haben, was darauf hinweist, dass das Modell besser abschneidet. Wie hängt die Konfusionsmatrix mit Präzision und Recall zusammen? Denken Sie daran, dass der oben gedruckte Klassifikationsbericht eine Präzision von 0,85 und einen Recall von 0,67 zeigte.

Präzision = tp / (tp + fp) = 22 / (22 + 4) = 0,8461538461538461

Recall = tp / (tp + fn) = 22 / (22 + 11) = 0,6666666666666666

✅ F: Wie hat das Modell laut der Konfusionsmatrix abgeschnitten? A: Gar nicht schlecht; es gibt eine gute Anzahl an True Negatives, aber auch ein paar False Negatives.

Lassen Sie uns die Begriffe, die wir zuvor gesehen haben, mit Hilfe der Zuordnung von TP/TN und FP/FN in der Konfusionsmatrix noch einmal betrachten:

🎓 Präzision: TP/(TP + FP) Der Anteil relevanter Instanzen unter den abgerufenen Instanzen (z. B. welche Labels korrekt zugeordnet wurden)

🎓 Recall: TP/(TP + FN) Der Anteil relevanter Instanzen, die abgerufen wurden, unabhängig davon, ob sie korrekt zugeordnet wurden oder nicht

🎓 f1-Score: (2 * Präzision * Recall)/(Präzision + Recall) Ein gewichteter Durchschnitt von Präzision und Recall, wobei 1 das Beste und 0 das Schlechteste ist

🎓 Support: Die Anzahl der Vorkommen jedes abgerufenen Labels

🎓 Genauigkeit: (TP + TN)/(TP + TN + FP + FN) Der Prozentsatz der Labels, die für eine Stichprobe korrekt vorhergesagt wurden.

🎓 Makro-Durchschnitt: Die Berechnung des ungewichteten Durchschnitts der Metriken für jedes Label, ohne das Ungleichgewicht der Labels zu berücksichtigen.

🎓 Gewichteter Durchschnitt: Die Berechnung des Durchschnitts der Metriken für jedes Label, wobei das Ungleichgewicht der Labels durch Gewichtung nach ihrem Support (der Anzahl der tatsächlichen Instanzen für jedes Label) berücksichtigt wird.

✅ Können Sie sich vorstellen, welche Metrik Sie beobachten sollten, wenn Sie die Anzahl der False Negatives reduzieren möchten?

Visualisierung der ROC-Kurve dieses Modells

🎥 Klicken Sie auf das obige Bild für eine kurze Videoübersicht zu ROC-Kurven

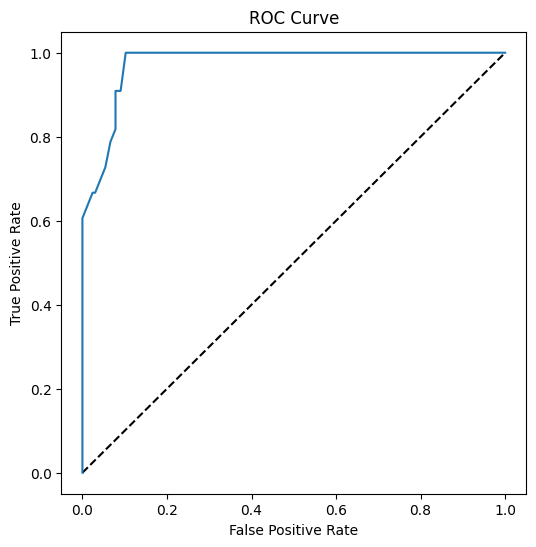
Lassen Sie uns eine weitere Visualisierung durchführen, um die sogenannte 'ROC'-Kurve zu sehen:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Verwenden Sie Matplotlib, um die Receiver Operating Characteristic oder ROC des Modells zu zeichnen. ROC-Kurven werden oft verwendet, um die Ausgabe eines Klassifikators in Bezug auf seine True Positives und False Positives zu betrachten. "ROC-Kurven zeigen typischerweise die True Positive Rate auf der Y-Achse und die False Positive Rate auf der X-Achse." Daher sind die Steilheit der Kurve und der Abstand zwischen der Mittellinie und der Kurve wichtig: Sie möchten eine Kurve, die schnell nach oben und über die Linie verläuft. In unserem Fall gibt es zunächst False Positives, und dann verläuft die Linie korrekt nach oben und darüber:

Verwenden Sie abschließend die roc_auc_score API von Scikit-learn, um die tatsächliche 'Fläche unter der Kurve' (AUC) zu berechnen:

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Das Ergebnis ist 0.9749908725812341. Da die AUC von 0 bis 1 reicht, möchten Sie einen hohen Wert erzielen, da ein Modell, das zu 100 % korrekte Vorhersagen trifft, eine AUC von 1 hat; in diesem Fall ist das Modell ziemlich gut.

In zukünftigen Lektionen zu Klassifikationen werden Sie lernen, wie Sie iterativ die Werte Ihres Modells verbessern können. Aber für den Moment: Herzlichen Glückwunsch! Sie haben diese Lektionen zur Regression abgeschlossen!

🚀Herausforderung

Es gibt noch viel mehr über logistische Regression zu entdecken! Aber der beste Weg zu lernen ist, zu experimentieren. Finden Sie einen Datensatz, der sich für diese Art der Analyse eignet, und erstellen Sie ein Modell damit. Was lernen Sie dabei? Tipp: Probieren Sie Kaggle für interessante Datensätze aus.

Quiz nach der Vorlesung

Rückblick & Selbststudium

Lesen Sie die ersten Seiten dieses Papiers von Stanford über einige praktische Anwendungen der logistischen Regression. Denken Sie über Aufgaben nach, die besser für die eine oder andere Art von Regression geeignet sind, die wir bisher studiert haben. Was würde am besten funktionieren?

Aufgabe

Wiederholen Sie diese Regression

Haftungsausschluss:
Dieses Dokument wurde mithilfe des KI-Übersetzungsdienstes Co-op Translator übersetzt. Obwohl wir uns um Genauigkeit bemühen, weisen wir darauf hin, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner ursprünglichen Sprache sollte als maßgebliche Quelle betrachtet werden. Für kritische Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die durch die Nutzung dieser Übersetzung entstehen.

24 KiB Raw Permalink Blame History Unescape Escape