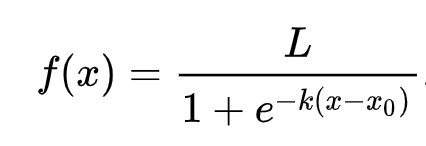22 KiB

Raw Permalink Blame History

Logistická regrese pro predikci kategorií

Kvíz před lekcí

Tato lekce je dostupná v R!

Úvod

V této poslední lekci o regresi, jedné ze základních klasických technik strojového učení, se podíváme na logistickou regresi. Tuto techniku byste použili k odhalení vzorců pro predikci binárních kategorií. Je tato cukrovinka čokoládová nebo ne? Je tato nemoc nakažlivá nebo ne? Vybere si tento zákazník tento produkt nebo ne?

V této lekci se naučíte:

Novou knihovnu pro vizualizaci dat
Techniky logistické regrese

✅ Prohlubte své znalosti práce s tímto typem regrese v tomto modulu Learn

Předpoklady

Po práci s daty o dýních jsme nyní dostatečně obeznámeni s tím, že existuje jedna binární kategorie, se kterou můžeme pracovat: Barva.

Postavme model logistické regrese, který bude predikovat, na základě některých proměnných, jakou barvu bude mít daná dýně (oranžová 🎃 nebo bílá 👻).

Proč mluvíme o binární klasifikaci v lekci o regresi? Pouze z jazykového pohodlí, protože logistická regrese je ve skutečnosti klasifikační metoda, i když založená na lineární regresi. O dalších způsobech klasifikace dat se dozvíte v další skupině lekcí.

Definujte otázku

Pro naše účely to vyjádříme jako binární: 'Bílá' nebo 'Ne bílá'. V našem datasetu je také kategorie 'pruhovaná', ale má málo záznamů, takže ji nebudeme používat. Stejně zmizí, jakmile odstraníme nulové hodnoty z datasetu.

🎃 Zajímavost: bílé dýně někdy nazýváme 'duchové' dýně. Nejsou příliš snadné na vyřezávání, takže nejsou tak populární jako oranžové, ale vypadají zajímavě! Mohli bychom tedy také formulovat naši otázku jako: 'Duch' nebo 'Ne duch'. 👻

O logistické regresi

Logistická regrese se liší od lineární regrese, kterou jste se naučili dříve, v několika důležitých ohledech.

🎥 Klikněte na obrázek výše pro krátký video přehled logistické regrese.

Binární klasifikace

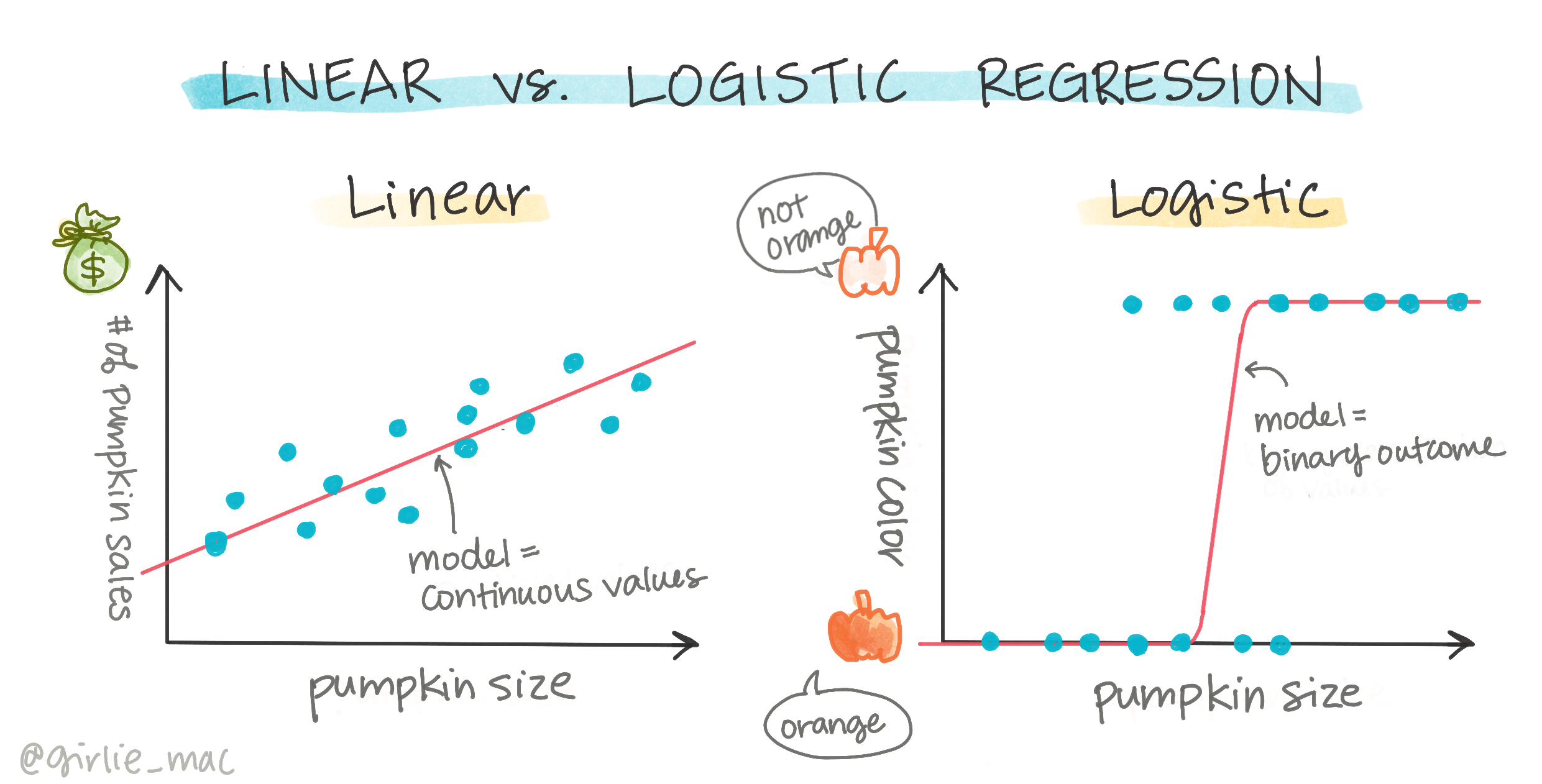
Logistická regrese nenabízí stejné funkce jako lineární regrese. První z nich nabízí predikci binární kategorie ("bílá nebo ne bílá"), zatímco druhá je schopna predikovat kontinuální hodnoty, například na základě původu dýně a času sklizně, o kolik se zvýší její cena.

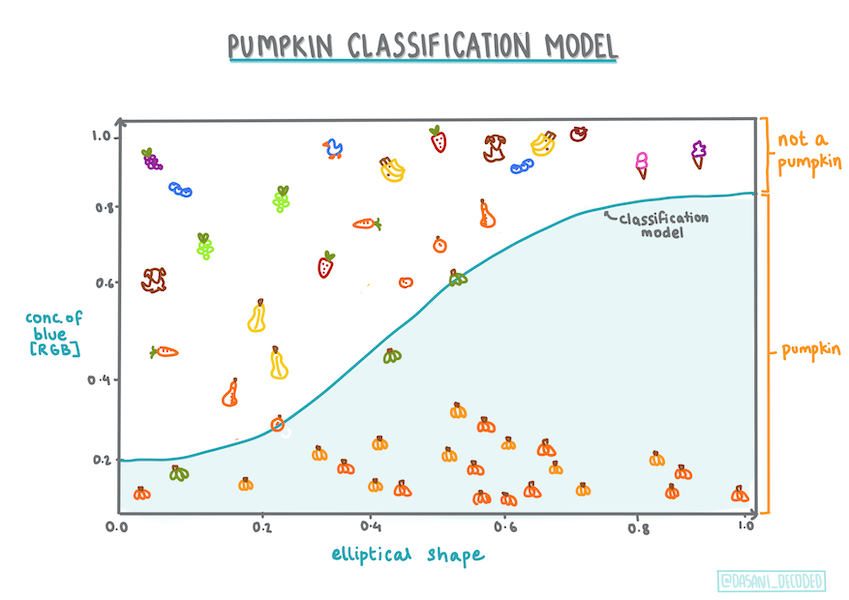
Infografika od Dasani Madipalli

Další klasifikace

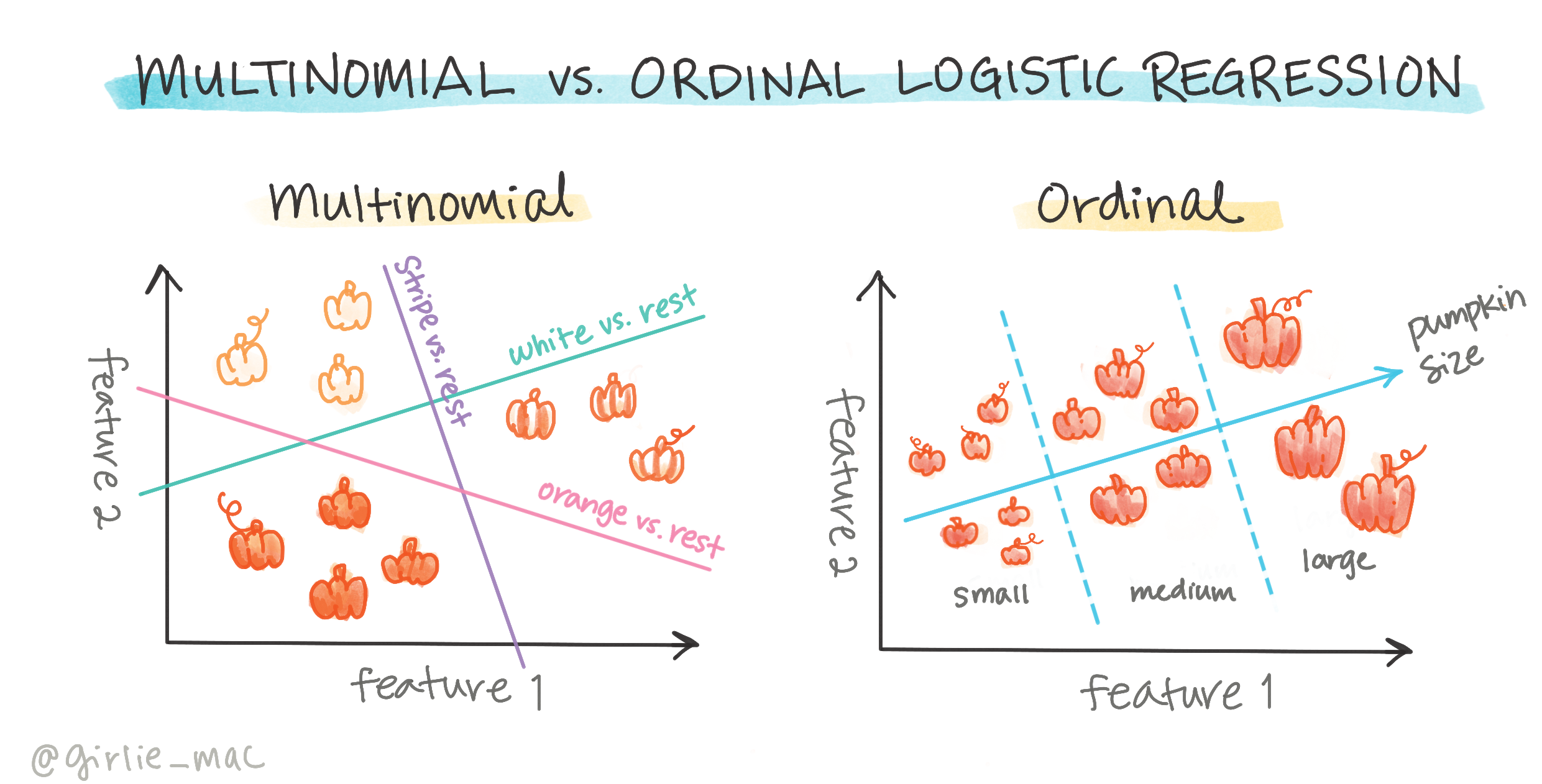
Existují i jiné typy logistické regrese, včetně multinomiální a ordinální:

Multinomiální, která zahrnuje více než jednu kategorii - "Oranžová, Bílá a Pruhovaná".
Ordinální, která zahrnuje uspořádané kategorie, užitečné, pokud bychom chtěli uspořádat naše výsledky logicky, například naše dýně, které jsou uspořádány podle konečného počtu velikostí (mini, sm, med, lg, xl, xxl).

Proměnné NEMUSÍ být korelované

Pamatujete si, jak lineární regrese fungovala lépe s více korelovanými proměnnými? Logistická regrese je opakem - proměnné nemusí být v souladu. To funguje pro tato data, která mají poměrně slabé korelace.

Potřebujete hodně čistých dat

Logistická regrese poskytne přesnější výsledky, pokud použijete více dat; náš malý dataset není pro tento úkol optimální, takže to mějte na paměti.

🎥 Klikněte na obrázek výše pro krátký video přehled přípravy dat pro lineární regresi

✅ Zamyslete se nad typy dat, které by se dobře hodily pro logistickou regresi

Cvičení - úprava dat

Nejprve data trochu vyčistěte, odstraňte nulové hodnoty a vyberte pouze některé sloupce:

Přidejte následující kód:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Vždy se můžete podívat na svůj nový dataframe:

pumpkins.info

Vizualizace - kategorický graf

Nyní jste načetli startovací notebook s daty o dýních a vyčistili jej tak, aby obsahoval dataset s několika proměnnými, včetně Barva. Vizualizujme dataframe v notebooku pomocí jiné knihovny: Seaborn, která je postavena na Matplotlib, který jsme použili dříve.

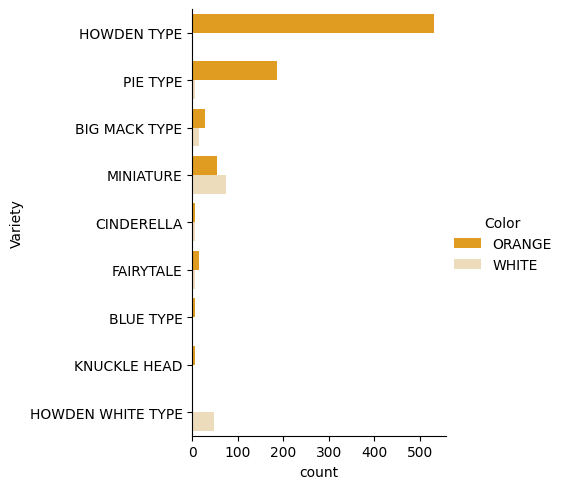
Seaborn nabízí zajímavé způsoby vizualizace vašich dat. Například můžete porovnat distribuce dat pro každou Variety a Color v kategorickém grafu.

Vytvořte takový graf pomocí funkce catplot, použijte naše data o dýních pumpkins a specifikujte barevné mapování pro každou kategorii dýní (oranžová nebo bílá):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Pozorováním dat můžete vidět, jak se data o barvě vztahují k odrůdě.

✅ Na základě tohoto kategorického grafu, jaké zajímavé průzkumy si dokážete představit?

Předzpracování dat: kódování vlastností a štítků

Náš dataset o dýních obsahuje textové hodnoty pro všechny své sloupce. Práce s kategorickými daty je intuitivní pro lidi, ale ne pro stroje. Algoritmy strojového učení dobře pracují s čísly. Proto je kódování velmi důležitým krokem ve fázi předzpracování dat, protože nám umožňuje převést kategorická data na číselná data, aniž bychom ztratili jakékoli informace. Dobré kódování vede k vytvoření dobrého modelu.

Pro kódování vlastností existují dva hlavní typy kodérů:

Ordinal encoder: hodí se dobře pro ordinální proměnné, což jsou kategorické proměnné, kde jejich data následují logické pořadí, jako je sloupec Item Size v našem datasetu. Vytváří mapování tak, že každá kategorie je reprezentována číslem, které odpovídá pořadí kategorie ve sloupci.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Categorical encoder: hodí se dobře pro nominální proměnné, což jsou kategorické proměnné, kde jejich data nenásledují logické pořadí, jako všechny vlastnosti kromě Item Size v našem datasetu. Jedná se o one-hot kódování, což znamená, že každá kategorie je reprezentována binárním sloupcem: kódovaná proměnná je rovna 1, pokud dýně patří do dané odrůdy, a 0 jinak.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Poté se ColumnTransformer použije k kombinaci více kodérů do jednoho kroku a jejich aplikaci na příslušné sloupce.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Na druhou stranu, pro kódování štítku používáme třídu LabelEncoder ze scikit-learn, což je užitečná třída pro normalizaci štítků tak, aby obsahovaly pouze hodnoty mezi 0 a n_classes-1 (zde 0 a 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Jakmile jsme zakódovali vlastnosti a štítek, můžeme je sloučit do nového dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Jaké jsou výhody použití ordinal encoderu pro sloupec Item Size?

Analýza vztahů mezi proměnnými

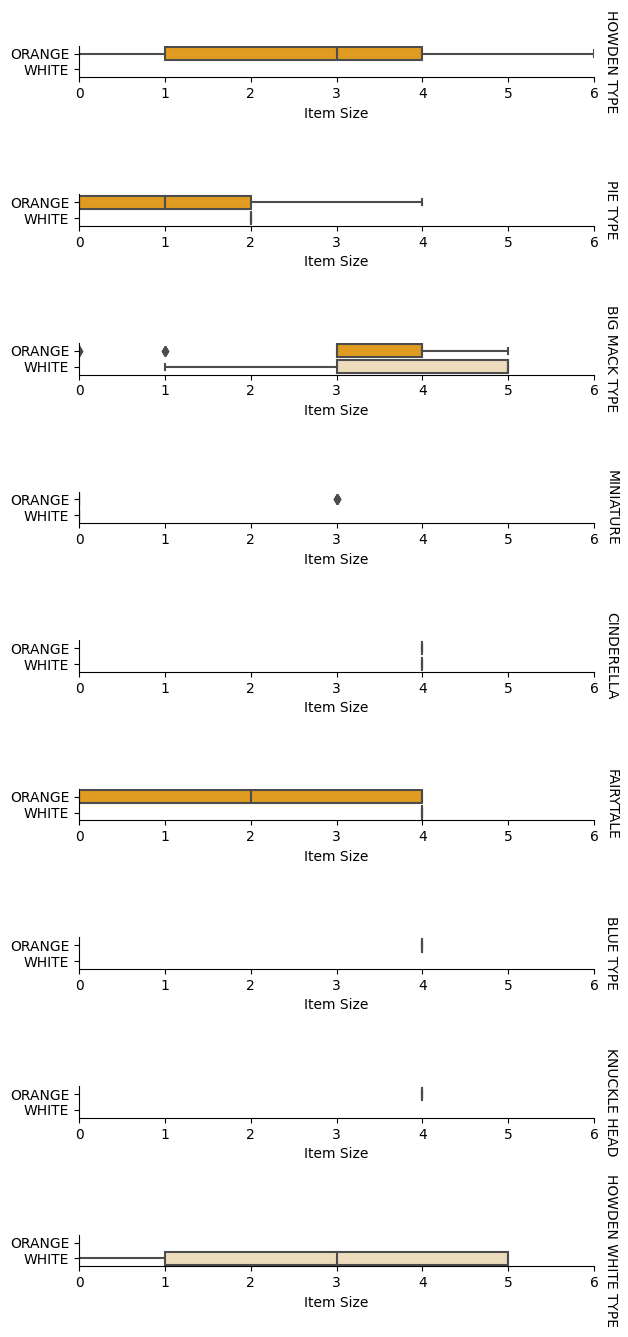
Nyní, když jsme předzpracovali naše data, můžeme analyzovat vztahy mezi vlastnostmi a štítkem, abychom získali představu o tom, jak dobře bude model schopen predikovat štítek na základě vlastností. Nejlepší způsob, jak provést tento typ analýzy, je vykreslení dat. Opět použijeme funkci catplot ze Seaborn, abychom vizualizovali vztahy mezi Item Size, Variety a Color v kategorickém grafu. Pro lepší vykreslení dat použijeme zakódovaný sloupec Item Size a nezakódovaný sloupec Variety.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Použití swarm plotu

Protože Color je binární kategorie (Bílá nebo Ne), potřebuje 'specializovaný přístup k vizualizaci'. Existují i jiné způsoby vizualizace vztahu této kategorie s ostatními proměnnými.

Můžete vizualizovat proměnné vedle sebe pomocí grafů Seaborn.

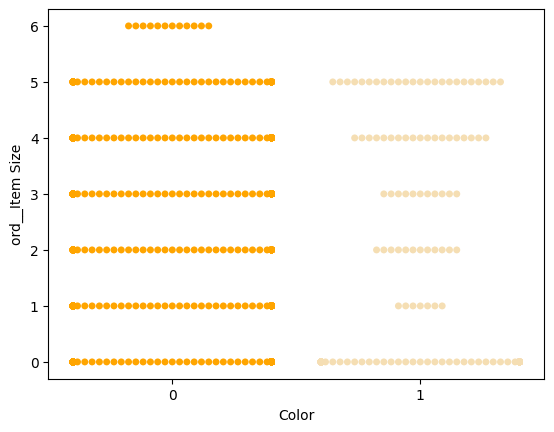
Vyzkoušejte 'swarm' plot pro zobrazení distribuce hodnot:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Pozor: výše uvedený kód může generovat varování, protože Seaborn nedokáže reprezentovat takové množství datových bodů ve swarm plotu. Možným řešením je zmenšení velikosti markeru pomocí parametru 'size'. Mějte však na paměti, že to ovlivňuje čitelnost grafu.

🧮 Matematika

Logistická regrese se opírá o koncept 'maximální věrohodnosti' pomocí sigmoidních funkcí. 'Sigmoidní funkce' na grafu vypadá jako tvar 'S'. Bere hodnotu a mapuje ji na něco mezi 0 a 1. Její křivka se také nazývá 'logistická křivka'. Její vzorec vypadá takto:

kde střed sigmoidní křivky se nachází na bodě 0 osy x, L je maximální hodnota křivky a k je strmost křivky. Pokud je výsledek funkce větší než 0,5, daný štítek bude přiřazen třídě '1' binární volby. Pokud ne, bude klasifikován jako '0'.

Vytvořte svůj model

Vytvoření modelu pro nalezení těchto binárních klasifikací je překvapivě jednoduché ve Scikit-learn.

🎥 Klikněte na obrázek výše pro krátký video přehled vytvoření modelu lineární regrese

Vyberte proměnné, které chcete použít ve svém klasifikačním modelu, a rozdělte trénovací a testovací sady pomocí train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Nyní můžete trénovat svůj model, zavolejte fit() s trénovacími daty a vytiskněte jeho výsledek:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Podívejte se na skóre svého modelu. Není špatné, vzhledem k tomu, že máte pouze asi 1000 řádků dat:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Lepší pochopení pomocí matice záměn

Zatímco můžete získat zprávu o skóre termíny vytištěním výše uvedených položek, můžete svůj model lépe pochopit pomocí matice záměn, která nám pomůže pochopit, jak model funguje.

🎓 'Matice záměn' (nebo 'matice chyb') je tabulka, která vyjadřuje skutečné vs. falešné pozitivní a negativní výsledky vašeho modelu, čímž hodnotí přesnost predikcí.

Pro použití matice záměn zavolejte confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Podívejte se na matici záměn svého modelu:

array([[162,   4],
       [ 11,  22]])

Ve Scikit-learn matice záměn: řádky (osa 0) jsou skutečné štítky a sloupce (osa 1) jsou predikované štítky.

	0	1
0	TN	FP
1	FN	TP

Co se zde děje? Řekněme, že náš model je požádán, aby klasifikoval dýně mezi dvě binární kategorie, kategorii 'bílá' a kategorii 'ne bílá'.

Pokud váš model predikuje dýni jako ne bílou a ve skutečnosti patří do kategorie 'ne bílá', nazýváme to pravý negativní výsledek, zobrazený horním levým číslem.
Pokud váš model predikuje dýni jako bílou a ve skutečnosti patří do kategorie 'ne bílá', nazýváme to falešný negativní výsledek, zobrazený dolním levým číslem.
Pokud váš model predikuje dýni jako ne bílou a ve skutečnosti patří do kategorie 'bílá', nazýváme to falešný pozitivní výsledek, zobrazený horním pravým číslem.
Pokud váš model predikuje dýni jako bílou a ve skutečnosti patří do kategorie 'bílá', nazýváme to pravý pozitivní výsledek, zobrazený dolním pravým číslem.

Jak jste možná uhodli, je preferováno mít větší počet pravých pozitivních a pravých negativních výsledků a nižší počet falešných pozitivních a falešných negativních výsledků, což znamená, že model funguje lépe. Jak souvisí matice záměny s přesností a úplností? Pamatujte, že výše uvedená zpráva o klasifikaci ukázala přesnost (0,85) a úplnost (0,67).

Přesnost = tp / (tp + fp) = 22 / (22 + 4) = 0,8461538461538461

Úplnost = tp / (tp + fn) = 22 / (22 + 11) = 0,6666666666666666

✅ Otázka: Jak si model vedl podle matice záměny? Odpověď: Docela dobře; je zde značný počet správně negativních, ale také několik falešně negativních.

Pojďme si znovu projít pojmy, které jsme viděli dříve, s pomocí mapování TP/TN a FP/FN v matici záměny:

🎓 Přesnost: TP/(TP + FP) Podíl relevantních instancí mezi získanými instancemi (např. které štítky byly správně označeny)

🎓 Úplnost: TP/(TP + FN) Podíl relevantních instancí, které byly získány, ať už správně označené nebo ne

🎓 f1-skóre: (2 * přesnost * úplnost)/(přesnost + úplnost) Vážený průměr přesnosti a úplnosti, přičemž nejlepší je 1 a nejhorší 0

🎓 Podpora: Počet výskytů každého získaného štítku

🎓 Přesnost: (TP + TN)/(TP + TN + FP + FN) Procento štítků správně předpovězených pro vzorek.

🎓 Makro průměr: Výpočet neváženého průměru metrik pro každý štítek, bez ohledu na nerovnováhu štítků.

🎓 Vážený průměr: Výpočet průměru metrik pro každý štítek, přičemž se bere v úvahu nerovnováha štítků jejich vážením podle podpory (počtu skutečných instancí pro každý štítek).

✅ Dokážete si představit, kterou metriku byste měli sledovat, pokud chcete, aby váš model snížil počet falešně negativních?

Vizualizace ROC křivky tohoto modelu

🎥 Klikněte na obrázek výše pro krátký video přehled ROC křivek

Pojďme udělat ještě jednu vizualizaci, abychom viděli tzv. 'ROC' křivku:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

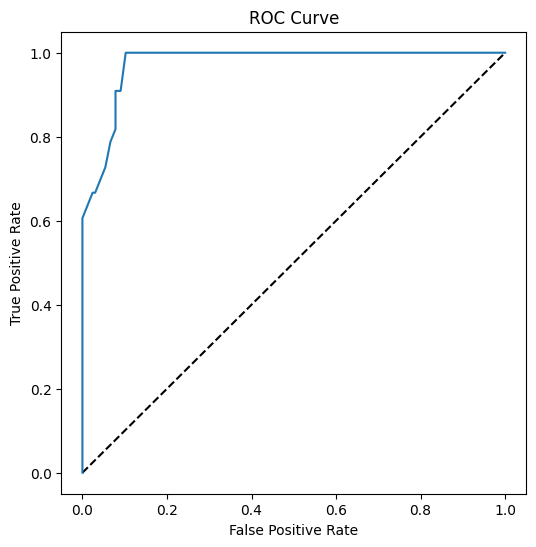
Pomocí Matplotlibu vykreslete Receiver Operating Characteristic nebo ROC modelu. ROC křivky se často používají k získání pohledu na výstup klasifikátoru z hlediska jeho správně vs. falešně pozitivních. "ROC křivky obvykle zobrazují míru správně pozitivních na ose Y a míru falešně pozitivních na ose X." Proto záleží na strmosti křivky a prostoru mezi středovou čarou a křivkou: chcete křivku, která rychle stoupá a přechází přes čáru. V našem případě jsou na začátku falešně pozitivní, a poté čára správně stoupá a přechází přes čáru:

Nakonec použijte Scikit-learn roc_auc_score API k výpočtu skutečné 'plochy pod křivkou' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Výsledek je 0.9749908725812341. Vzhledem k tomu, že AUC se pohybuje od 0 do 1, chcete vysoké skóre, protože model, který je ve svých předpovědích 100% správný, bude mít AUC 1; v tomto případě je model docela dobrý.

V budoucích lekcích o klasifikacích se naučíte, jak iterovat a zlepšovat skóre svého modelu. Ale prozatím gratulujeme! Dokončili jste tyto lekce o regresi!

🚀Výzva

Logistická regrese nabízí mnoho dalších možností! Nejlepší způsob, jak se učit, je experimentovat. Najděte datovou sadu, která se hodí k tomuto typu analýzy, a vytvořte s ní model. Co jste se naučili? tip: zkuste Kaggle pro zajímavé datové sady.

Kvíz po přednášce

Přehled & Samostudium

Přečtěte si první několik stránek tohoto článku ze Stanfordu o některých praktických využitích logistické regrese. Přemýšlejte o úlohách, které jsou lépe vhodné pro jeden nebo druhý typ regresních úloh, které jsme dosud studovali. Co by fungovalo nejlépe?

Úkol

Znovu vyzkoušejte tuto regresi

Prohlášení:
Tento dokument byl přeložen pomocí služby pro automatický překlad Co-op Translator. Ačkoli se snažíme o přesnost, mějte prosím na paměti, že automatické překlady mohou obsahovat chyby nebo nepřesnosti. Původní dokument v jeho původním jazyce by měl být považován za autoritativní zdroj. Pro důležité informace doporučujeme profesionální lidský překlad. Neodpovídáme za žádná nedorozumění nebo nesprávné interpretace vyplývající z použití tohoto překladu.

22 KiB Raw Permalink Blame History