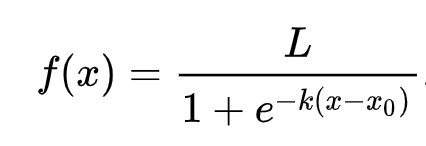34 KiB

Raw Permalink Blame History Unescape Escape

Логистична регресия за предсказване на категории

Тест преди лекцията

Този урок е наличен и на R!

Въведение

В този последен урок за регресия, една от основните класически техники в машинното обучение, ще разгледаме логистичната регресия. Тази техника се използва за откриване на модели за предсказване на бинарни категории. Това бонбонче шоколад ли е или не? Тази болест заразна ли е или не? Този клиент ще избере този продукт или не?

В този урок ще научите:

Нова библиотека за визуализация на данни
Техники за логистична регресия

✅ Задълбочете разбирането си за работа с този тип регресия в този модул за обучение

Предпоставки

След като вече работихме с данните за тиквите, сме достатъчно запознати с тях, за да осъзнаем, че има една бинарна категория, с която можем да работим: Цвят.

Нека изградим модел за логистична регресия, за да предскажем, въз основа на някои променливи, какъв цвят вероятно ще има дадена тиква (оранжева 🎃 или бяла 👻).

Защо говорим за бинарна класификация в урок за регресия? Само за езиково удобство, тъй като логистичната регресия е всъщност метод за класификация, макар и базиран на линейни модели. Научете за други начини за класифициране на данни в следващата група уроци.

Определяне на въпроса

За нашите цели ще изразим това като бинарно: 'Бяла' или 'Не бяла'. В нашия набор от данни има и категория 'райета', но има малко случаи на нея, така че няма да я използваме. Тя така или иначе изчезва, след като премахнем стойностите null от набора от данни.

🎃 Забавен факт: понякога наричаме белите тикви 'призрачни' тикви. Те не са много лесни за издълбаване, затова не са толкова популярни като оранжевите, но изглеждат страхотно! Така че можем да преформулираме въпроса си като: 'Призрачна' или 'Не призрачна'. 👻

За логистичната регресия

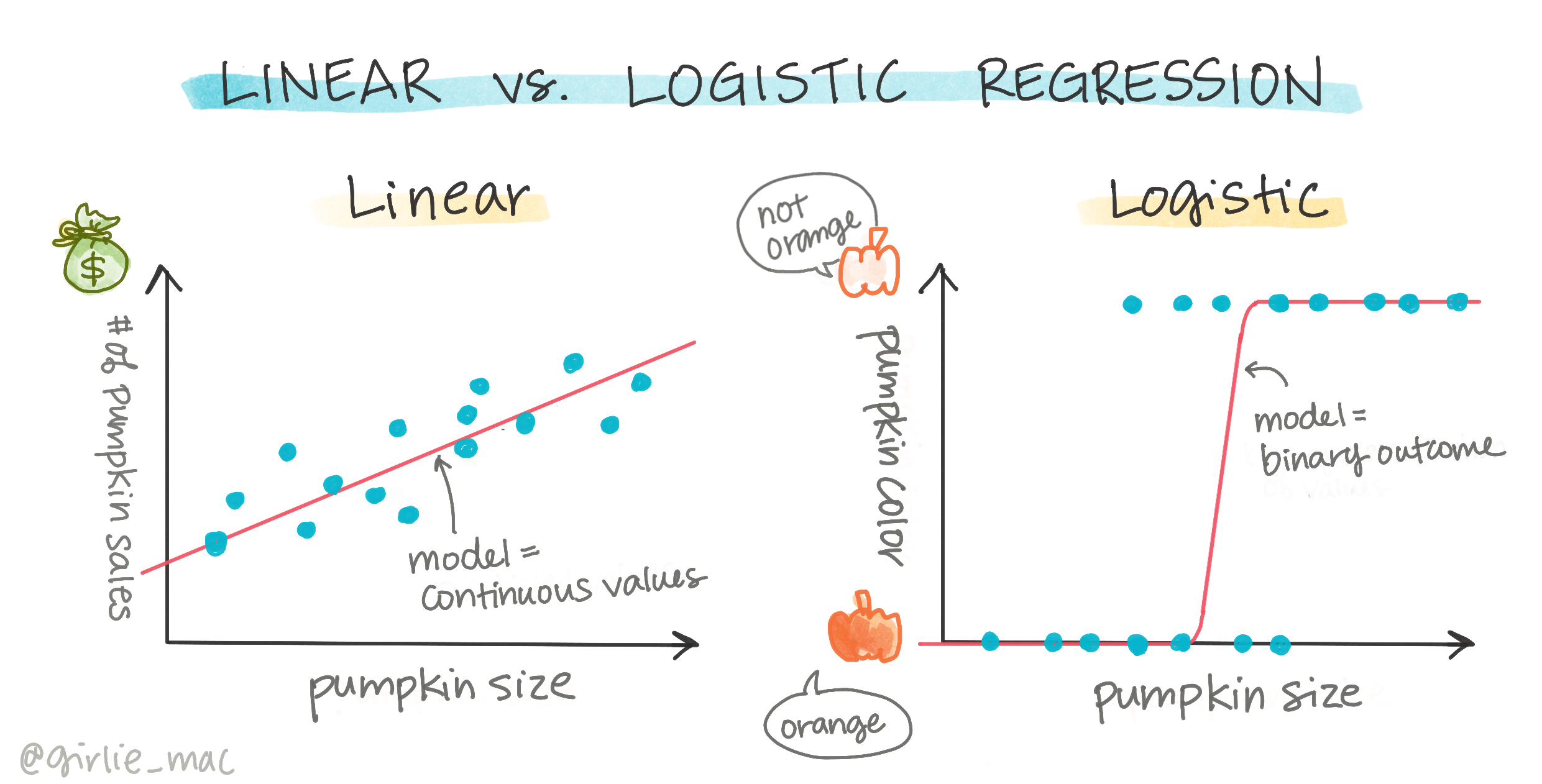
Логистичната регресия се различава от линейната регресия, която разгледахме по-рано, по няколко важни начина.

🎥 Кликнете върху изображението по-горе за кратко видео за логистичната регресия.

Бинарна класификация

Логистичната регресия не предлага същите функции като линейната регресия. Първата предлага предсказание за бинарна категория ("бяла или не бяла"), докато втората е способна да предсказва непрекъснати стойности, например въз основа на произхода на тиквата и времето на прибиране на реколтата, колко ще се повиши цената ѝ.

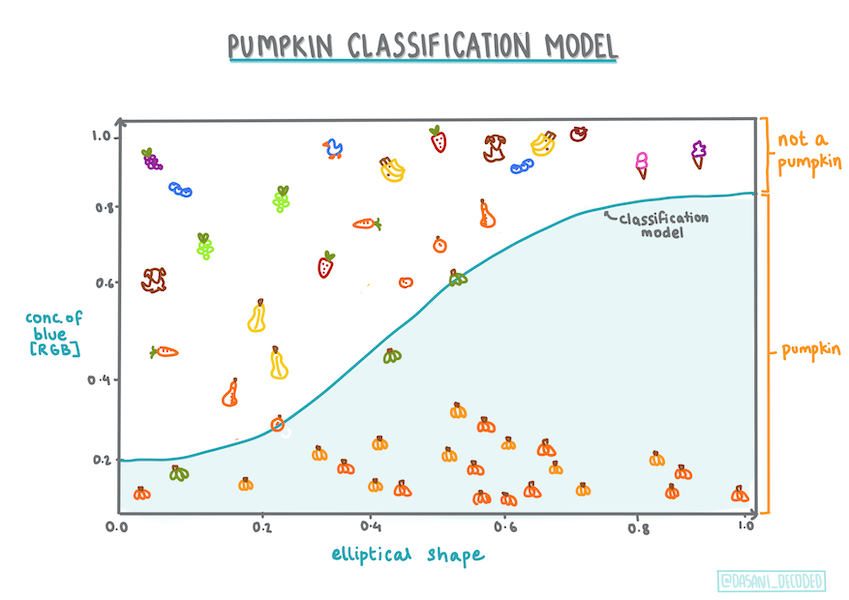
Инфографика от Dasani Madipalli

Други класификации

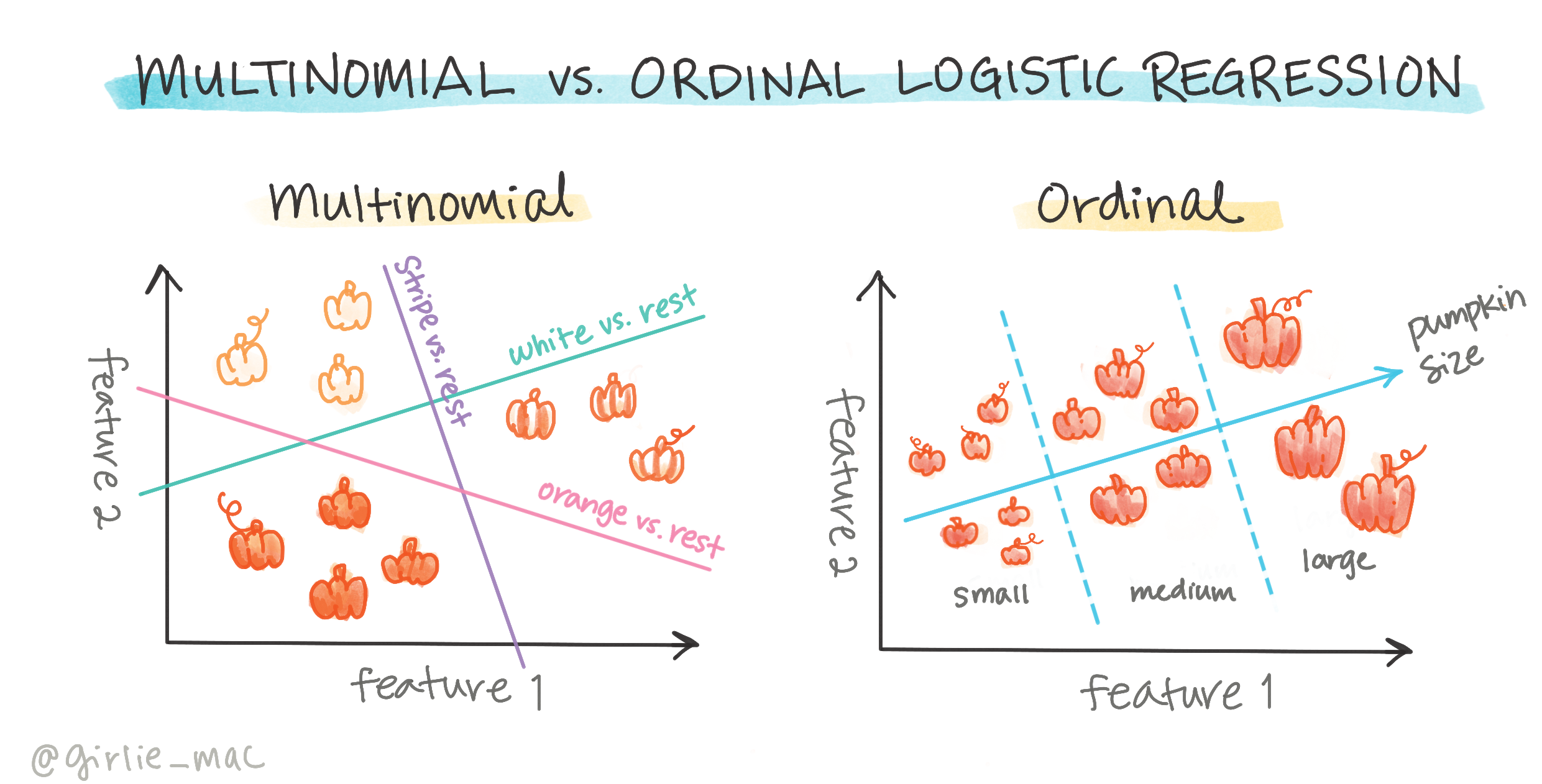
Има и други видове логистична регресия, включително мултиноминална и ординална:

Мултиноминална, която включва повече от една категория - "Оранжева, Бяла и Райета".
Ординална, която включва подредени категории, полезна ако искаме да подредим резултатите си логично, като например тиквите, които са подредени по ограничен брой размери (мини, малък, среден, голям, XL, XXL).

Променливите НЕ трябва да корелират

Помните ли как линейната регресия работеше по-добре с повече корелирани променливи? Логистичната регресия е обратното - променливите не трябва да се подреждат. Това работи за тези данни, които имат сравнително слаби корелации.

Нуждаете се от много чисти данни

Логистичната регресия ще даде по-точни резултати, ако използвате повече данни; нашият малък набор от данни не е оптимален за тази задача, така че имайте това предвид.

✅ Помислете за типовете данни, които биха били подходящи за логистична регресия.

Упражнение - подредете данните

Първо, почистете данните, като премахнете стойностите null и изберете само някои от колоните:

Добавете следния код:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Винаги можете да погледнете новия си dataframe:

pumpkins.info

Визуализация - категоричен график

Досега сте заредили началния notebook с данни за тикви и сте го почистили, за да запазите набор от данни, съдържащ няколко променливи, включително Цвят. Нека визуализираме dataframe-а в notebook-а, използвайки различна библиотека: Seaborn, която е изградена върху Matplotlib, която използвахме по-рано.

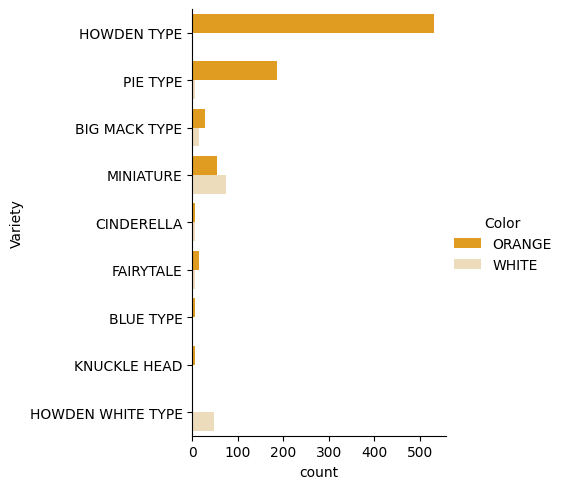
Seaborn предлага някои интересни начини за визуализация на данните. Например, можете да сравните разпределенията на данните за всяка Разновидност и Цвят в категоричен график.

Създайте такъв график, като използвате функцията catplot, използвайки данните за тиквите pumpkins, и задайте цветово картографиране за всяка категория тикви (оранжева или бяла):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Наблюдавайки данните, можете да видите как данните за цвета се отнасят към разновидността.

✅ Въз основа на този категоричен график, какви интересни изследвания можете да си представите?

Предварителна обработка на данни: кодиране на характеристики и етикети

Нашият набор от данни за тикви съдържа текстови стойности за всички свои колони. Работата с категорични данни е интуитивна за хората, но не и за машините. Алгоритмите за машинно обучение работят добре с числа. Затова кодирането е много важна стъпка в етапа на предварителна обработка на данни, тъй като ни позволява да превърнем категоричните данни в числови, без да губим информация. Добро кодиране води до изграждане на добър модел.

За кодиране на характеристики има два основни типа кодиращи:

Ординален кодиращ: подходящ за ординални променливи, които са категорични променливи, при които данните следват логическа подредба, като колоната Размер на артикула в нашия набор от данни. Той създава картографиране, така че всяка категория да бъде представена с число, което е редът на категорията в колоната.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Категоричен кодиращ: подходящ за номинални променливи, които са категорични променливи, при които данните не следват логическа подредба, като всички характеристики, различни от Размер на артикула в нашия набор от данни. Това е кодиране с единичен бит, което означава, че всяка категория е представена с бинарна колона: кодираната променлива е равна на 1, ако тиквата принадлежи към тази разновидност, и 0 в противен случай.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

След това ColumnTransformer се използва за комбиниране на множество кодиращи в една стъпка и прилагането им към съответните колони.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

От друга страна, за кодиране на етикета използваме класа LabelEncoder от scikit-learn, който е помощен клас за нормализиране на етикетите, така че те да съдържат само стойности между 0 и n_classes-1 (тук, 0 и 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

След като сме кодирали характеристиките и етикета, можем да ги обединим в нов dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Какви са предимствата на използването на ординален кодиращ за колоната Размер на артикула?

Анализ на връзките между променливите

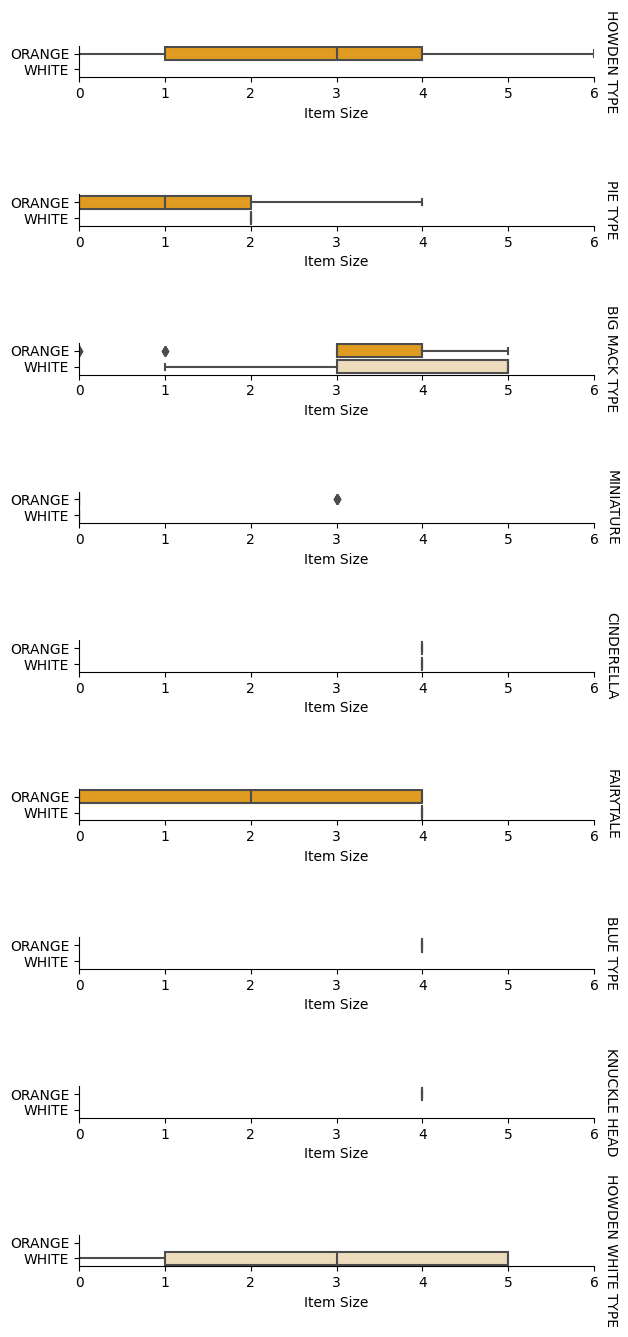
Сега, когато сме обработили данните, можем да анализираме връзките между характеристиките и етикета, за да добием представа колко добре моделът ще може да предскаже етикета въз основа на характеристиките. Най-добрият начин за извършване на този вид анализ е чрез визуализиране на данните. Ще използваме отново функцията catplot от Seaborn, за да визуализираме връзките между Размер на артикула, Разновидност и Цвят в категоричен график. За по-добро визуализиране на данните ще използваме кодираната колона Размер на артикула и некодираната колона Разновидност.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Използване на swarm график

Тъй като Цвят е бинарна категория (Бяла или Не), тя изисква 'специализиран подход за визуализация'. Има други начини за визуализиране на връзката на тази категория с други променливи.

Можете да визуализирате променливите една до друга с графики от Seaborn.

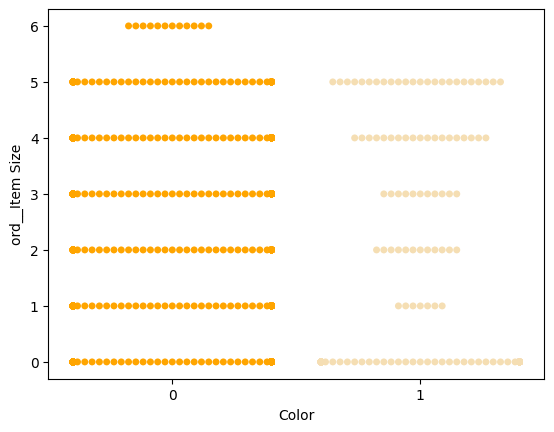
Опитайте swarm график, за да покажете разпределението на стойностите:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Внимание: кодът по-горе може да генерира предупреждение, тъй като Seaborn не успява да представи такова количество точки в swarm график. Възможно решение е намаляване на размера на маркера, като се използва параметърът 'size'. Въпреки това, имайте предвид, че това влияе върху четливостта на графика.

🧮 Покажете ми математиката

Логистичната регресия разчита на концепцията за 'максимална вероятност', използвайки сигмоидни функции. Сигмоидната функция на график изглежда като форма на 'S'. Тя взема стойност и я картографира между 0 и 1. Нейната крива се нарича още 'логистична крива'. Формулата ѝ изглежда така:

където средната точка на сигмоида се намира при x = 0, L е максималната стойност на кривата, а k е стръмността на кривата. Ако резултатът от функцията е повече от 0.5, етикетът ще бъде класифициран като '1' от бинарния избор. Ако не, ще бъде класифициран като '0'.

Изградете своя модел

Изграждането на модел за намиране на тези бинарни класификации е изненадващо лесно в Scikit-learn.

🎥 Кликнете върху изображението по-горе за кратко видео за изграждане на модел за линейна регресия.

Изберете променливите, които искате да използвате в модела си за класификация, и разделете тренировъчния и тестовия набор, като извикате train_test_split():
```
from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```

Сега можете да обучите модела си, като извикате fit() с тренировъчните данни, и да отпечатате резултата му:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Вижте резултатите на модела си. Не е зле, като се има предвид, че имате само около 1000 реда данни:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

По-добро разбиране чрез матрица на объркване

Докато можете да получите отчет за резултатите термини, като отпечатате горните елементи, може да разберете модела си по-лесно, като използвате матрица на объркване, за да ни помогне да разберем как се представя моделът.

🎓 'Матрица на объркване' (или 'матрица на грешки') е таблица, която изразява истинските срещу фалшивите положителни и отрицателни резултати на модела, като по този начин оценява точността на предсказанията.

За да използвате матрица на объркване, извикайте confusion_matrix():
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)
```
Вижте матрицата на объркване на модела си:
```
array([[162,   4],
       [ 11,  22]])
```

В Scikit-learn, редовете (ос 0) са действителните етикети, а колоните (ос 1) са предсказаните етикети.

	0	1
0	TN	FP
1	FN	TP

Какво се случва тук? Да кажем, че моделът ни е помолен да класифицира тикви между две бинарни категории, категория 'бяла' и категория 'не бяла'.

Ако моделът ви предскаже тиква като не бяла и тя принадлежи към категория 'не бяла' в действителност, наричаме това истински отрицателен резултат, показан от горния ляв номер.
Ако моделът ви предскаже тиква като бяла и тя принадлежи към категория 'не бяла' в действителност, наричаме това фалшив отрицателен резултат, показан от долния ляв номер.
Ако моделът ви предскаже тиква като не бяла и тя принадлежи към категория 'бяла' в действителност, наричаме това фалшив положителен резултат, показан от горния десен номер.
Ако моделът ви предскаже тиква като бяла и тя принадлежи към категория 'бяла' в действителност, наричаме това истински положителен резултат, показан от долния десен номер.

Както може би сте се досетили, е за предпочитане да имате по-голям брой истински положителни и истински отрицателни резултати и по-малък брой фалшиви положителни и фалшиви Как се свързва матрицата на объркване с прецизността и припомнянето? Запомнете, че отчетът за класификация, отпечатан по-горе, показа прецизност (0.85) и припомняне (0.67).

Прецизност = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Припомняне = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ Въпрос: Според матрицата на объркване, как се справи моделът? Отговор: Не е зле; има добър брой истински отрицателни, но също така и няколко фалшиви отрицателни.

Нека отново разгледаме термините, които видяхме по-рано, с помощта на картографирането на TP/TN и FP/FN в матрицата на объркване:

🎓 Прецизност: TP/(TP + FP) Делът на релевантните случаи сред извлечените случаи (например кои етикети са добре етикетирани).

🎓 Припомняне: TP/(TP + FN) Делът на релевантните случаи, които са извлечени, независимо дали са добре етикетирани или не.

🎓 f1-оценка: (2 * прецизност * припомняне)/(прецизност + припомняне) Претеглена средна стойност на прецизността и припомнянето, като най-добрата е 1, а най-лошата е 0.

🎓 Поддръжка: Броят на случаите за всяка извлечена етикетирана категория.

🎓 Точност: (TP + TN)/(TP + TN + FP + FN) Процентът на етикетите, предсказани правилно за дадена извадка.

🎓 Средна макро стойност: Изчисляване на невзетата предвид средна стойност на метриките за всяка категория, без да се отчита дисбалансът на етикетите.

🎓 Претеглена средна стойност: Изчисляване на средната стойност на метриките за всяка категория, като се отчита дисбалансът на етикетите чрез претегляне спрямо тяхната поддръжка (броя на истинските случаи за всяка категория).

✅ Можете ли да се сетите коя метрика трябва да наблюдавате, ако искате вашият модел да намали броя на фалшивите отрицателни?

Визуализирайте ROC кривата на този модел

🎥 Кликнете върху изображението по-горе за кратък видео преглед на ROC кривите.

Нека направим още една визуализация, за да видим така наречената 'ROC' крива:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

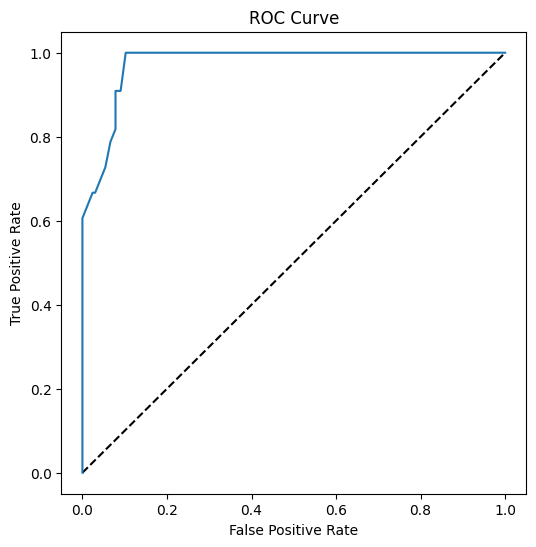
С помощта на Matplotlib начертайте Receiving Operating Characteristic или ROC на модела. ROC кривите често се използват, за да се получи представа за изхода на класификатора по отношение на неговите истински срещу фалшиви положителни. "ROC кривите обикновено показват истинския положителен процент на Y оста и фалшивия положителен процент на X оста." Следователно, стръмността на кривата и пространството между средната линия и кривата са важни: искате крива, която бързо се издига и преминава над линията. В нашия случай има фалшиви положителни в началото, след което линията се издига и преминава правилно:

Накрая, използвайте roc_auc_score API на Scikit-learn, за да изчислите действителната 'Площ под кривата' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Резултатът е 0.9749908725812341. Като се има предвид, че AUC варира от 0 до 1, искате висок резултат, тъй като модел, който е 100% точен в своите предсказания, ще има AUC от 1; в този случай моделът е доста добър.

В бъдещи уроци за класификации ще научите как да подобрите резултатите на вашия модел. Но засега, поздравления! Завършихте тези уроци за регресия!

🚀Предизвикателство

Има още много за разглеждане относно логистичната регресия! Но най-добрият начин да научите е чрез експериментиране. Намерете набор от данни, който е подходящ за този тип анализ, и изградете модел с него. Какво научавате? съвет: опитайте Kaggle за интересни набори от данни.

Тест след лекцията

Преглед и самостоятелно обучение

Прочетете първите няколко страници от тази статия от Станфорд за някои практически приложения на логистичната регресия. Помислете за задачи, които са по-подходящи за един или друг тип регресионни задачи, които сме изучавали досега. Какво би работило най-добре?

Задание

Повторно изпълнение на тази регресия

Отказ от отговорност:
Този документ е преведен с помощта на AI услуга за превод Co-op Translator. Въпреки че се стремим към точност, моля, имайте предвид, че автоматизираните преводи може да съдържат грешки или неточности. Оригиналният документ на неговия роден език трябва да се счита за авторитетен източник. За критична информация се препоръчва професионален човешки превод. Не носим отговорност за недоразумения или погрешни интерпретации, произтичащи от използването на този превод.

34 KiB Raw Permalink Blame History Unescape Escape