29 KiB

Raw Permalink Blame History Unescape Escape

Катание на CartPole

Проблема, которую мы решали на предыдущем занятии, может показаться игрушечной задачей, не имеющей реального применения. Но это не так, потому что многие реальные проблемы также имеют аналогичный сценарий — включая игры в шахматы или го. Они похожи, потому что у нас также есть доска с заданными правилами и дискретным состоянием.

Предварительный тест

Введение

На этом уроке мы применим те же принципы Q-обучения к задаче с непрерывным состоянием, то есть состоянием, заданным одним или несколькими вещественными числами. Мы будем работать с следующей задачей:

Задача: Если Питер хочет убежать от волка, ему нужно двигаться быстрее. Мы увидим, как Питер может научиться кататься на коньках, особенно поддерживать равновесие, используя Q-обучение.

Питер и его друзья проявляют креативность, чтобы убежать от волка! Изображение от Jen Looper

Мы будем использовать упрощенную версию задачи балансировки, известную как проблема CartPole. В мире cartpole у нас есть горизонтальный слайдер, который может двигаться влево или вправо, и цель состоит в том, чтобы удерживать вертикальную палку на вершине слайдера.

Предварительные требования

На этом уроке мы будем использовать библиотеку OpenAI Gym для симуляции различных сред. Вы можете запустить код этого урока локально (например, из Visual Studio Code), в этом случае симуляция откроется в новом окне. При запуске кода онлайн вам, возможно, придется внести некоторые изменения в код, как описано здесь.

OpenAI Gym

На предыдущем занятии правила игры и состояние задавались классом Board, который мы определили сами. Здесь мы будем использовать специальную симуляционную среду, которая будет моделировать физику, стоящую за балансировкой палки. Одна из самых популярных симуляционных сред для обучения алгоритмов обучения с подкреплением называется Gym, которая поддерживается OpenAI. Используя этот гимнастический зал, мы можем создавать различные среды, от симуляции cartpole до игр Atari.

Примечание: Вы можете увидеть другие доступные среды от OpenAI Gym здесь.

Сначала давайте установим gym и импортируем необходимые библиотеки (кодовый блок 1):

import sys
!{sys.executable} -m pip install gym 

import gym
import matplotlib.pyplot as plt
import numpy as np
import random

Упражнение - инициализация среды cartpole

Чтобы работать с задачей балансировки cartpole, нам нужно инициализировать соответствующую среду. Каждая среда связана с:

Пространством наблюдений, которое определяет структуру информации, которую мы получаем от среды. Для задачи cartpole мы получаем положение палки, скорость и некоторые другие значения.
Пространством действий, которое определяет возможные действия. В нашем случае пространство действий дискретно и состоит из двух действий - влево и вправо. (кодовый блок 2)

Чтобы инициализировать, введите следующий код:

env = gym.make("CartPole-v1")
print(env.action_space)
print(env.observation_space)
print(env.action_space.sample())

Чтобы увидеть, как работает среда, давайте запустим короткую симуляцию на 100 шагов. На каждом шаге мы предоставляем одно из действий, которое нужно выполнить - в этой симуляции мы просто случайным образом выбираем действие из action_space.

Запустите код ниже и посмотрите, к чему это приведет.

✅ Помните, что предпочтительнее запускать этот код на локальной установке Python! (кодовый блок 3)
```
env.reset()

for i in range(100):
   env.render()
   env.step(env.action_space.sample())
env.close()
```
Вы должны увидеть что-то похожее на это изображение:
Во время симуляции нам нужно получать наблюдения, чтобы решить, как действовать. На самом деле функция step возвращает текущие наблюдения, функцию награды и флаг завершения, который указывает, имеет ли смысл продолжать симуляцию или нет: (кодовый блок 4)
```
env.reset()

done = False
while not done:
   env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   print(f"{obs} -> {rew}")
env.close()
```
В выводе блокнота вы увидите что-то вроде этого:
```
[ 0.03403272 -0.24301182  0.02669811  0.2895829 ] -> 1.0
[ 0.02917248 -0.04828055  0.03248977  0.00543839] -> 1.0
[ 0.02820687  0.14636075  0.03259854 -0.27681916] -> 1.0
[ 0.03113408  0.34100283  0.02706215 -0.55904489] -> 1.0
[ 0.03795414  0.53573468  0.01588125 -0.84308041] -> 1.0
...
[ 0.17299878  0.15868546 -0.20754175 -0.55975453] -> 1.0
[ 0.17617249  0.35602306 -0.21873684 -0.90998894] -> 1.0
```
Вектор наблюдений, который возвращается на каждом шаге симуляции, содержит следующие значения:
- Положение слайдера
- Скорость слайдера
- Угол палки
- Скорость вращения палки
Получите минимальное и максимальное значение этих чисел: (кодовый блок 5)
```
print(env.observation_space.low)
print(env.observation_space.high)
```
Вы также можете заметить, что значение награды на каждом шаге симуляции всегда равно 1. Это потому, что наша цель - выжить как можно дольше, т.е. удерживать палку в относительно вертикальном положении как можно дольше.

✅ На самом деле симуляция CartPole считается решенной, если нам удается получить среднюю награду 195 за 100 последовательных попыток.

Дискретизация состояния

В Q-обучении нам нужно построить Q-таблицу, которая определяет, что делать в каждом состоянии. Чтобы иметь возможность это сделать, состояние должно быть дискретным, точнее, оно должно содержать конечное число дискретных значений. Таким образом, нам нужно как-то дискретизировать наши наблюдения, сопоставляя их с конечным набором состояний.

Существует несколько способов сделать это:

Разделить на корзины. Если мы знаем интервал определенного значения, мы можем разделить этот интервал на несколько корзин, а затем заменить значение номером корзины, к которой оно принадлежит. Это можно сделать с помощью метода numpy digitize. В этом случае мы точно будем знать размер состояния, потому что он будет зависеть от количества корзин, которые мы выберем для цифровизации.

✅ Мы можем использовать линейную интерполяцию, чтобы привести значения к некоторому конечному интервалу (скажем, от -20 до 20), а затем преобразовать числа в целые числа, округляя их. Это дает нам немного меньше контроля над размером состояния, особенно если мы не знаем точные диапазоны входных значений. Например, в нашем случае 2 из 4 значений не имеют верхних/нижних границ, что может привести к бесконечному числу состояний.

В нашем примере мы воспользуемся вторым подходом. Как вы можете заметить позже, несмотря на неопределенные верхние/нижние границы, эти значения редко принимают значения вне определенных конечных интервалов, таким образом, эти состояния с экстремальными значениями будут очень редкими.

Вот функция, которая возьмет наблюдение из нашей модели и создаст кортеж из 4 целых значений: (кодовый блок 6)
```
def discretize(x):
    return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int))
```

Давайте также исследуем другой метод дискретизации с использованием корзин: (кодовый блок 7)

def create_bins(i,num):
    return np.arange(num+1)*(i[1]-i[0])/num+i[0]

print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10))

ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter
nbins = [20,20,10,10] # number of bins for each parameter
bins = [create_bins(ints[i],nbins[i]) for i in range(4)]

def discretize_bins(x):
    return tuple(np.digitize(x[i],bins[i]) for i in range(4))

Теперь давайте запустим короткую симуляцию и наблюдать за этими дискретными значениями среды. Не стесняйтесь попробовать как discretize and discretize_bins, так и посмотреть, есть ли разница.

✅ discretize_bins возвращает номер корзины, который начинается с 0. Таким образом, для значений входной переменной около 0 он возвращает номер из середины интервала (10). В discretize мы не заботились о диапазоне выходных значений, позволяя им быть отрицательными, таким образом, значения состояния не сдвинуты, и 0 соответствует 0. (кодовый блок 8)
```
env.reset()

done = False
while not done:
   #env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   #print(discretize_bins(obs))
   print(discretize(obs))
env.close()
```
✅ Раскомментируйте строку, начинающуюся с env.render, если хотите увидеть, как среда выполняется. В противном случае вы можете выполнить это в фоновом режиме, что быстрее. Мы будем использовать это "невидимое" выполнение во время нашего процесса Q-обучения.

Структура Q-таблицы

На нашем предыдущем занятии состояние было простой парой чисел от 0 до 8, и поэтому было удобно представлять Q-таблицу в виде тензора numpy с формой 8x8x2. Если мы используем дискретизацию по корзинам, размер нашего вектора состояния также известен, так что мы можем использовать тот же подход и представлять состояние в виде массива формы 20x20x10x10x2 (здесь 2 - это размерность пространства действий, а первые размеры соответствуют количеству корзин, которые мы выбрали для использования для каждого из параметров в пространстве наблюдений).

Однако иногда точные размеры пространства наблюдений неизвестны. В случае функции discretize мы никогда не можем быть уверены, что наше состояние остается в пределах определенных границ, потому что некоторые из оригинальных значений не ограничены. Таким образом, мы будем использовать немного другой подход и представлять Q-таблицу в виде словаря.

Используйте пару (состояние, действие) в качестве ключа словаря, а значение будет соответствовать значению записи в Q-таблице. (кодовый блок 9)
```
Q = {}
actions = (0,1)

def qvalues(state):
    return [Q.get((state,a),0) for a in actions]
```
Здесь мы также определяем функцию qvalues(), которая возвращает список значений Q-таблицы для данного состояния, соответствующего всем возможным действиям. Если запись отсутствует в Q-таблице, мы вернем 0 по умолчанию.

Начнем Q-обучение

Теперь мы готовы научить Питера балансировать!

Сначала давайте установим некоторые гиперпараметры: (кодовый блок 10)
```
# hyperparameters
alpha = 0.3
gamma = 0.9
epsilon = 0.90
```
Здесь, вектор alpha is the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreased alpha to lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjusting alpha values later.

gamma is the discount factor that shows to which extent we should prioritize future reward over current reward.

epsilon is the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will in epsilon percent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.

✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"

Improve the algorithm

We can also make two improvements to our algorithm from the previous lesson:

Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
Calculate maximum average cumulative result, Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.

Collect all cumulative rewards at each simulation at rewards для дальнейшей визуализации. (кодовый блок 11)

def probs(v,eps=1e-4):
    v = v-v.min()+eps
    v = v/v.sum()
    return v

Qmax = 0
cum_rewards = []
rewards = []
for epoch in range(100000):
    obs = env.reset()
    done = False
    cum_reward=0
    # == do the simulation ==
    while not done:
        s = discretize(obs)
        if random.random()<epsilon:
            # exploitation - chose the action according to Q-Table probabilities
            v = probs(np.array(qvalues(s)))
            a = random.choices(actions,weights=v)[0]
        else:
            # exploration - randomly chose the action
            a = np.random.randint(env.action_space.n)

        obs, rew, done, info = env.step(a)
        cum_reward+=rew
        ns = discretize(obs)
        Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns)))
    cum_rewards.append(cum_reward)
    rewards.append(cum_reward)
    # == Periodically print results and calculate average reward ==
    if epoch%5000==0:
        print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}")
        if np.average(cum_rewards) > Qmax:
            Qmax = np.average(cum_rewards)
            Qbest = Q
        cum_rewards=[]

Что вы можете заметить из этих результатов:

Близко к нашей цели. Мы очень близки к достижению цели получения 195 совокупных наград за 100+ последовательных запусков симуляции, или, возможно, мы уже достигли этого! Даже если мы получим меньшие числа, мы все равно не знаем, потому что мы усредняем по 5000 запускам, и только 100 запусков требуется по формальным критериям.
Награда начинает падать. Иногда награда начинает падать, что означает, что мы можем "разрушить" уже изученные значения в Q-таблице теми, которые ухудшают ситуацию.

Это наблюдение более четко видно, если мы построим график прогресса обучения.

Построение графика прогресса обучения

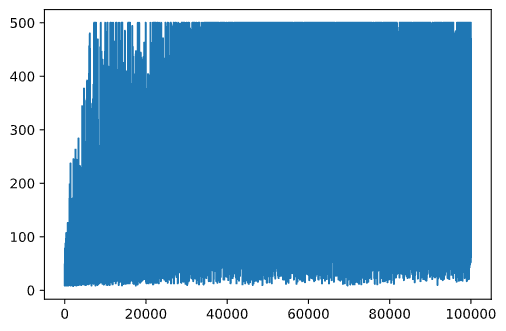
Во время обучения мы собирали значение совокупной награды на каждой из итераций в вектор rewards. Вот как это выглядит, когда мы строим его в зависимости от номера итерации:

plt.plot(rewards)

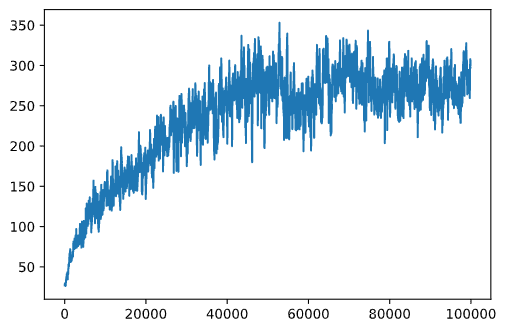
С этого графика невозможно ничего сказать, потому что из-за природы стохастического процесса обучения длина обучающих сессий сильно варьируется. Чтобы лучше понять этот график, мы можем вычислить скользящее среднее по серии экспериментов, скажем, 100. Это можно удобно сделать с помощью np.convolve: (кодовый блок 12)

def running_average(x,window):
    return np.convolve(x,np.ones(window)/window,mode='valid')

plt.plot(running_average(rewards,100))

Изменение гиперпараметров

Чтобы сделать обучение более стабильным, имеет смысл настроить некоторые из наших гиперпараметров во время обучения. В частности:

Для скорости обучения, alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values.
Increase epsilon. We may want to increase the epsilon slowly, in order to explore less and exploit more. It probably makes sense to start with lower value of epsilon, и поднимите до почти 1.

Задание 1: Поэкспериментируйте с значениями гиперпараметров и посмотрите, сможете ли вы достичь более высокой совокупной награды. Вы получаете больше 195?

Задание 2: Чтобы формально решить задачу, вам нужно получить 195 среднюю награду за 100 последовательных запусков. Измерьте это во время обучения и убедитесь, что вы формально решили задачу!

Увидеть результат в действии

Было бы интересно на самом деле увидеть, как ведет себя обученная модель. Давайте запустим симуляцию и будем следовать той же стратегии выбора действий, что и во время обучения, выбирая согласно распределению вероятностей в Q-таблице: (кодовый блок 13)

obs = env.reset()
done = False
while not done:
   s = discretize(obs)
   env.render()
   v = probs(np.array(qvalues(s)))
   a = random.choices(actions,weights=v)[0]
   obs,_,done,_ = env.step(a)
env.close()

Вы должны увидеть что-то подобное:

🚀Задача

Задание 3: Здесь мы использовали финальную копию Q-таблицы, которая может быть не лучшей. Помните, что мы сохранили Q-таблицу с наилучшей производительностью в Qbest variable! Try the same example with the best-performing Q-Table by copying Qbest over to Q and see if you notice the difference.

Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using np.argmax функции, чтобы узнать номер действия, соответствующего наивысшему значению Q-таблицы. Реализуйте эту стратегию и посмотрите, улучшит ли это балансировку.

Пост-лекционный тест

Задание

Обучите горный автомобиль

Заключение

Теперь мы узнали, как обучать агентов для достижения хороших результатов, просто предоставляя им функцию награды, которая определяет желаемое состояние игры, и предоставляя им возможность интеллектуально исследовать пространство поиска. Мы успешно применили алгоритм Q-обучения в случаях дискретных и непрерывных сред, но с дискретными действиями.

Важно также изучить ситуации, когда состояние действия также непрерывно, и когда пространство наблюдений гораздо более сложно, например, изображение с экрана игры Atari. В этих проблемах нам часто нужно использовать более мощные методы машинного обучения, такие как нейронные сети, для достижения хороших результатов. Эти более продвинутые темы будут предметом нашего предстоящего более продвинутого курса по ИИ.

Отказ от ответственности:
Этот документ был переведен с использованием машинных переводческих сервисов на основе ИИ. Хотя мы стремимся к точности, пожалуйста, имейте в виду, что автоматические переводы могут содержать ошибки или неточности. Оригинальный документ на родном языке следует считать авторитетным источником. Для критически важной информации рекомендуется профессиональный человеческий перевод. Мы не несем ответственности за любые недоразумения или неверные истолкования, возникающие в результате использования этого перевода.

29 KiB Raw Permalink Blame History Unescape Escape