22 KiB

Raw Permalink Blame History Unescape Escape

Прогнозирование временных рядов с использованием регрессора опорных векторов

В предыдущем уроке вы узнали, как использовать модель ARIMA для прогнозирования временных рядов. Теперь вы рассмотрите модель регрессора опорных векторов, которая используется для предсказания непрерывных данных.

Викторина перед лекцией

Введение

В этом уроке вы откроете для себя специфический способ построения моделей с использованием SVM: Опорные Вектора Машина для регрессии, или SVR: Регрессор опорных векторов.

SVR в контексте временных рядов ¹

Прежде чем понять важность SVR в прогнозировании временных рядов, вот некоторые важные концепции, которые вам нужно знать:

Регрессия: Метод контролируемого обучения для предсказания непрерывных значений из заданного набора входных данных. Идея заключается в том, чтобы подогнать кривую (или линию) в пространстве признаков, которая имеет максимальное количество точек данных. Нажмите здесь для получения дополнительной информации.
Операционная машина опорных векторов (SVM): Тип модели машинного обучения с контролем, используемый для классификации, регрессии и обнаружения выбросов. Модель представляет собой гиперплоскость в пространстве признаков, которая в случае классификации действует как граница, а в случае регрессии - как линия наилучшего соответствия. В SVM обычно используется функция ядра для преобразования набора данных в пространство более высокого числа измерений, чтобы их можно было легко разделить. Нажмите здесь для получения дополнительной информации о SVM.
Регрессор опорных векторов (SVR): Тип SVM, который находит линию наилучшего соответствия (которая в случае SVM является гиперплоскостью), имеющую максимальное количество точек данных.

Почему SVR? ¹

В прошлом уроке вы узнали о ARIMA, которая является очень успешным статистическим линейным методом для прогнозирования данных временных рядов. Однако во многих случаях данные временных рядов имеют нелинейность, которую нельзя смоделировать линейными моделями. В таких случаях способность SVM учитывать нелинейность данных для задач регрессии делает SVR успешным в прогнозировании временных рядов.

Упражнение - постройте модель SVR

Первые несколько шагов подготовки данных такие же, как в предыдущем уроке о ARIMA.

Откройте папку /working в этом уроке и найдите файл notebook.ipynb.²

Запустите блокнот и импортируйте необходимые библиотеки: ²

import sys
sys.path.append('../../')

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from sklearn.svm import SVR
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape

Загрузите данные из файла /data/energy.csv в dataframe Pandas и посмотрите на них: ²
```
energy = load_data('../../data')[['load']]
```
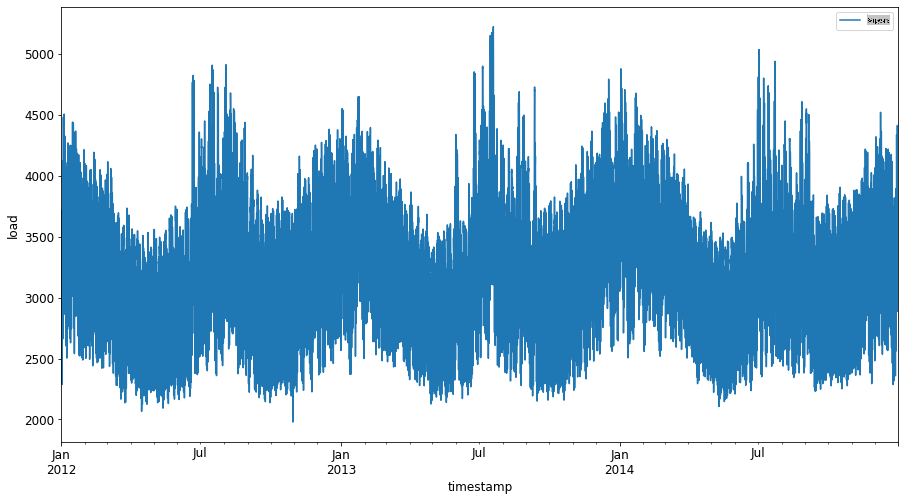
Постройте график всех доступных данных по энергии с января 2012 года по декабрь 2014 года: ²
```
energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Теперь давайте создадим нашу модель SVR.

Создание обучающих и тестовых наборов данных

Теперь, когда ваши данные загружены, вы можете разделить их на обучающие и тестовые наборы. Затем вы измените форму данных, чтобы создать набор данных на основе временных шагов, который будет необходим для SVR. Вы будете обучать свою модель на обучающем наборе. После завершения обучения модели вы оцените ее точность на обучающем наборе, тестовом наборе, а затем на полном наборе данных, чтобы увидеть общую производительность. Вам нужно убедиться, что тестовый набор охватывает более поздний период времени по сравнению с обучающим набором, чтобы гарантировать, что модель не получает информацию из будущих временных периодов ² (ситуация, известная как Переобучение).

Выделите двухмесячный период с 1 сентября по 31 октября 2014 года для обучающего набора. Тестовый набор будет включать двухмесячный период с 1 ноября по 31 декабря 2014 года: ²
```
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
```

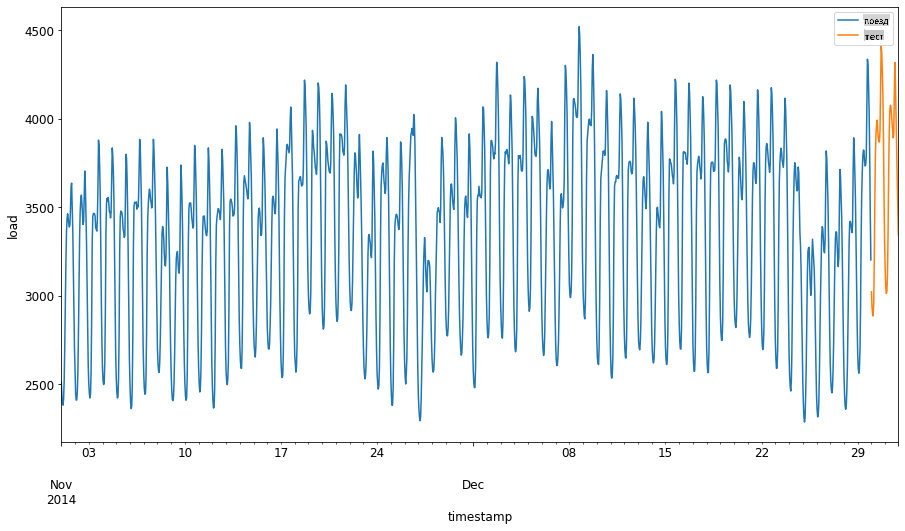
Визуализируйте различия: ²

energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

Подготовка данных для обучения

Теперь вам нужно подготовить данные для обучения, выполнив фильтрацию и масштабирование ваших данных. Отфильтруйте свой набор данных, чтобы включить только необходимые временные периоды и столбцы, и выполните масштабирование, чтобы гарантировать, что данные проецируются в интервале 0,1.

Отфильтруйте оригинальный набор данных, чтобы включить только упомянутые временные периоды для каждого набора и только нужный столбец 'load' плюс дату: ²

train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)

Training data shape:  (1416, 1)
Test data shape:  (48, 1)

Масштабируйте обучающие данные, чтобы они находились в диапазоне (0, 1): ²
```
scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
```
Теперь масштабируйте тестовые данные: ²
```
test['load'] = scaler.transform(test)
```

Создание данных с временными шагами ¹

Для SVR вы преобразуете входные данные в форму [batch, timesteps]. So, you reshape the existing train_data and test_data, так чтобы появилась новая размерность, которая относится к временным шагам.

# Converting to numpy arrays
train_data = train.values
test_data = test.values

В этом примере мы берем timesteps = 5. Таким образом, входными данными для модели являются данные за первые 4 временных шага, а выходными данными будут данные за 5-й временной шаг.

timesteps=5

Преобразование обучающих данных в 2D тензор с использованием вложенного спискового выражения:

train_data_timesteps=np.array([[j for j in train_data[i:i+timesteps]] for i in range(0,len(train_data)-timesteps+1)])[:,:,0]
train_data_timesteps.shape

(1412, 5)

Преобразование тестовых данных в 2D тензор:

test_data_timesteps=np.array([[j for j in test_data[i:i+timesteps]] for i in range(0,len(test_data)-timesteps+1)])[:,:,0]
test_data_timesteps.shape

(44, 5)

Выбор входных и выходных данных из обучающих и тестовых данных:

x_train, y_train = train_data_timesteps[:,:timesteps-1],train_data_timesteps[:,[timesteps-1]]
x_test, y_test = test_data_timesteps[:,:timesteps-1],test_data_timesteps[:,[timesteps-1]]

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

(1412, 4) (1412, 1)
(44, 4) (44, 1)

Реализация SVR ¹

Теперь пришло время реализовать SVR. Чтобы узнать больше об этой реализации, вы можете обратиться к этой документации. Для нашей реализации мы следуем следующим шагам:

Определите модель, вызвав функцию SVR() and passing in the model hyperparameters: kernel, gamma, c and epsilon
Prepare the model for the training data by calling the fit() function
Make predictions calling the predict()

Теперь мы создаем модель SVR. Здесь мы используем ядро RBF и устанавливаем гиперпараметры gamma, C и epsilon равными 0.5, 10 и 0.05 соответственно.

model = SVR(kernel='rbf',gamma=0.5, C=10, epsilon = 0.05)

Подгонка модели на обучающих данных ¹

model.fit(x_train, y_train[:,0])

SVR(C=10, cache_size=200, coef0=0.0, degree=3, epsilon=0.05, gamma=0.5,
    kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

Прогнозирование модели ¹

y_train_pred = model.predict(x_train).reshape(-1,1)
y_test_pred = model.predict(x_test).reshape(-1,1)

print(y_train_pred.shape, y_test_pred.shape)

(1412, 1) (44, 1)

Вы построили свой SVR! Теперь нам нужно его оценить.

Оценка вашей модели ¹

Для оценки сначала мы вернем данные к исходному масштабу. Затем, чтобы проверить производительность, мы построим график оригинальных и предсказанных временных рядов, а также напечатаем результат MAPE.

Масштабируйте предсказанный и оригинальный вывод:

# Scaling the predictions
y_train_pred = scaler.inverse_transform(y_train_pred)
y_test_pred = scaler.inverse_transform(y_test_pred)

print(len(y_train_pred), len(y_test_pred))

# Scaling the original values
y_train = scaler.inverse_transform(y_train)
y_test = scaler.inverse_transform(y_test)

print(len(y_train), len(y_test))

Проверьте производительность модели на обучающих и тестовых данных ¹

Мы извлекаем временные метки из набора данных, чтобы показать их по оси x нашего графика. Обратите внимание, что мы используем первые timesteps-1 значения в качестве входных данных для первого вывода, поэтому временные метки для вывода начнутся после этого.

train_timestamps = energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)].index[timesteps-1:]
test_timestamps = energy[test_start_dt:].index[timesteps-1:]

print(len(train_timestamps), len(test_timestamps))

1412 44

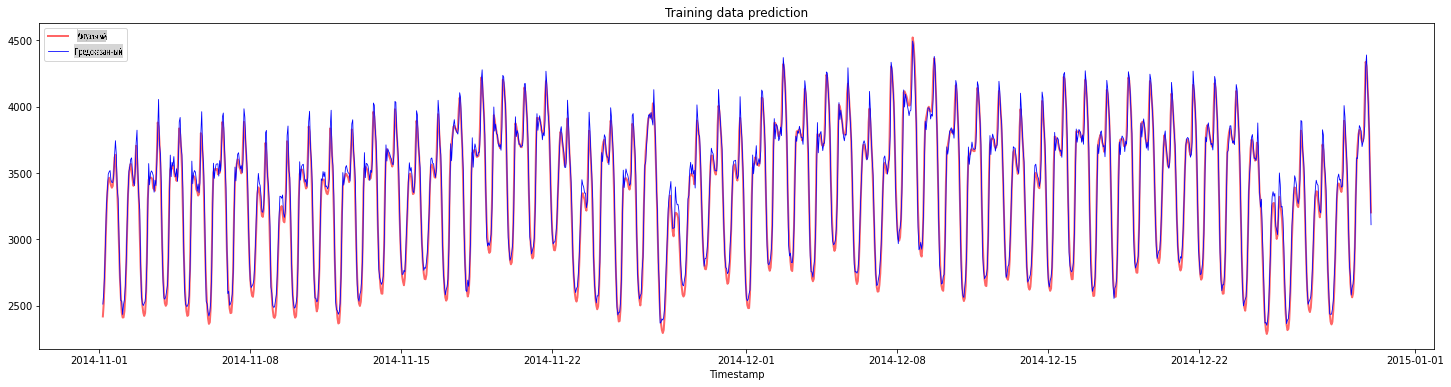
Постройте прогнозы для обучающих данных:

plt.figure(figsize=(25,6))
plt.plot(train_timestamps, y_train, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(train_timestamps, y_train_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.title("Training data prediction")
plt.show()

Выведите MAPE для обучающих данных

print('MAPE for training data: ', mape(y_train_pred, y_train)*100, '%')

MAPE for training data: 1.7195710200875551 %

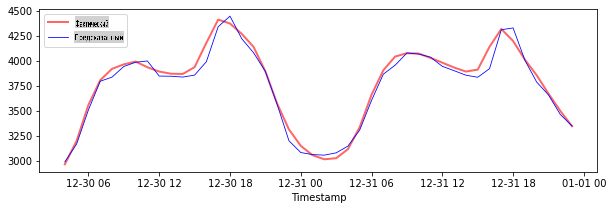
Постройте прогнозы для тестовых данных

plt.figure(figsize=(10,3))
plt.plot(test_timestamps, y_test, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(test_timestamps, y_test_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

Выведите MAPE для тестовых данных

print('MAPE for testing data: ', mape(y_test_pred, y_test)*100, '%')

MAPE for testing data:  1.2623790187854018 %

🏆 У вас очень хороший результат на тестовом наборе данных!

Проверьте производительность модели на полном наборе данных ¹

# Extracting load values as numpy array
data = energy.copy().values

# Scaling
data = scaler.transform(data)

# Transforming to 2D tensor as per model input requirement
data_timesteps=np.array([[j for j in data[i:i+timesteps]] for i in range(0,len(data)-timesteps+1)])[:,:,0]
print("Tensor shape: ", data_timesteps.shape)

# Selecting inputs and outputs from data
X, Y = data_timesteps[:,:timesteps-1],data_timesteps[:,[timesteps-1]]
print("X shape: ", X.shape,"\nY shape: ", Y.shape)

Tensor shape:  (26300, 5)
X shape:  (26300, 4) 
Y shape:  (26300, 1)

# Make model predictions
Y_pred = model.predict(X).reshape(-1,1)

# Inverse scale and reshape
Y_pred = scaler.inverse_transform(Y_pred)
Y = scaler.inverse_transform(Y)

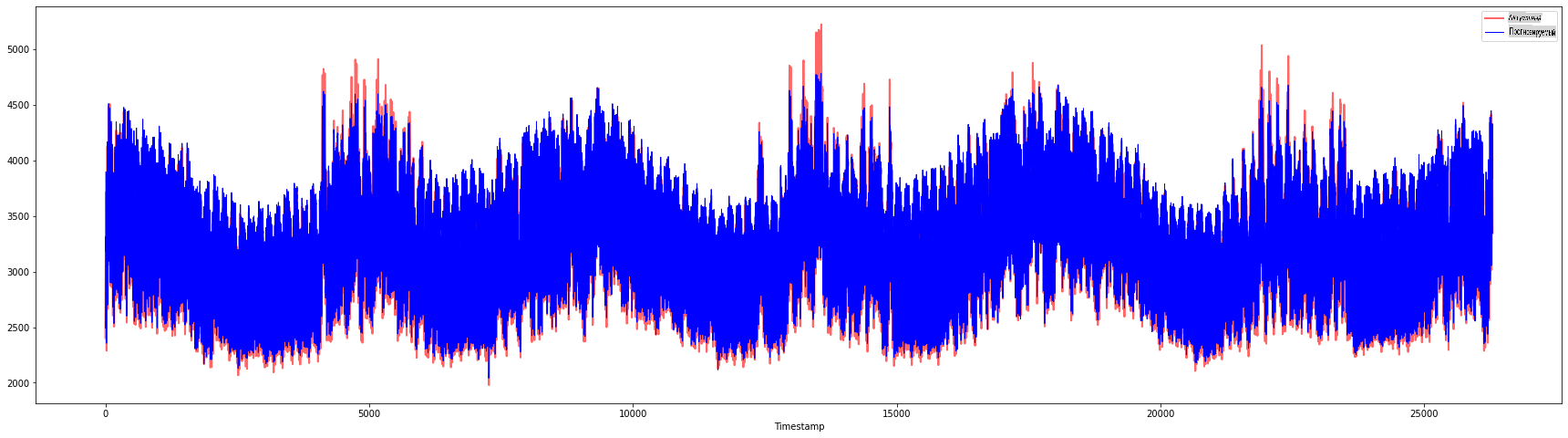
plt.figure(figsize=(30,8))
plt.plot(Y, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(Y_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

print('MAPE: ', mape(Y_pred, Y)*100, '%')

MAPE:  2.0572089029888656 %

🏆 Очень хорошие графики, показывающие модель с хорошей точностью. Отличная работа!

🚀Вызов

Попробуйте изменить гиперпараметры (gamma, C, epsilon) при создании модели и оцените данные, чтобы увидеть, какой набор гиперпараметров дает лучшие результаты на тестовых данных. Чтобы узнать больше об этих гиперпараметрах, вы можете обратиться к документу здесь.
Попробуйте использовать разные функции ядра для модели и проанализируйте их производительность на наборе данных. Полезный документ можно найти здесь.
Попробуйте использовать разные значения для timesteps в модели, чтобы сделать прогноз.

Викторина после лекции

Обзор и самообучение

Этот урок был посвящен применению SVR для прогнозирования временных рядов. Чтобы узнать больше о SVR, вы можете обратиться к этому блогу. Эта документация по scikit-learn предоставляет более полное объяснение о SVM в целом, SVR и также другие детали реализации, такие как различные функции ядра, которые можно использовать, и их параметры.

Задание

Новая модель SVR

Авторы

Отказ от ответственности:
Этот документ был переведен с использованием услуг машинного перевода на основе ИИ. Хотя мы стремимся к точности, пожалуйста, имейте в виду, что автоматические переводы могут содержать ошибки или неточности. Оригинальный документ на его родном языке следует считать авторитетным источником. Для критически важной информации рекомендуется профессиональный человеческий перевод. Мы не несем ответственности за любые недоразумения или неправильные толкования, возникающие в результате использования этого перевода.

Текст, код и вывод в этом разделе был предоставлен @AnirbanMukherjeeXD ↩︎
Текст, код и вывод в этом разделе были взяты из ARIMA ↩︎

22 KiB Raw Permalink Blame History Unescape Escape