27 KiB

Raw Permalink Blame History Unescape Escape

Прогнозирование временных рядов с помощью ARIMA

На предыдущем уроке вы узнали немного о прогнозировании временных рядов и загрузили набор данных, показывающий колебания электрической нагрузки за определённый период времени.

🎥 Нажмите на изображение выше, чтобы посмотреть видео: Краткое введение в модели ARIMA. Пример выполнен на R, но концепции универсальны.

Викторина перед лекцией

Введение

В этом уроке вы узнаете о специфическом способе построения моделей с помощью ARIMA: AutoRegressive Integrated Moving Average. Модели ARIMA особенно подходят для анализа данных, которые демонстрируют нестационарность.

Общие концепции

Чтобы работать с ARIMA, необходимо знать несколько ключевых понятий:

🎓 Стационарность. В статистическом контексте стационарность относится к данным, распределение которых не меняется при смещении во времени. Нестационарные данные, таким образом, показывают колебания из-за трендов, которые необходимо преобразовать для анализа. Сезонность, например, может вводить колебания в данные и может быть устранена с помощью процесса "сезонного дифференцирования".
🎓 Дифференцирование. Дифференцирование данных, опять же в статистическом контексте, относится к процессу преобразования нестационарных данных в стационарные путём удаления их нестабильного тренда. "Дифференцирование устраняет изменения в уровне временного ряда, устраняя тренд и сезонность и, следовательно, стабилизируя среднее значение временного ряда." Статья Шисюнга и др.

ARIMA в контексте временных рядов

Давайте разберём части ARIMA, чтобы лучше понять, как она помогает нам моделировать временные ряды и делать прогнозы.

AR - для АвтоРегрессии. Автогрессионные модели, как подразумевает название, смотрят "назад" во времени, чтобы проанализировать предыдущие значения в ваших данных и сделать предположения о них. Эти предыдущие значения называются "задержками". Примером может быть данные, показывающие ежемесячные продажи карандашей. Общая сумма продаж за каждый месяц будет считаться "изменяющейся переменной" в наборе данных. Эта модель строится на основе "изменяющейся переменной интереса, которая регрессируется на свои собственные запаздывающие (т.е. предыдущие) значения." wikipedia
I - для Интегрированной. В отличие от похожих моделей 'ARMA', 'I' в ARIMA относится к её интегрированному аспекту. Данные считаются "интегрированными", когда применяются шаги дифференцирования для устранения нестационарности.
MA - для Скользящего среднего. Аспект скользящего среднего в этой модели относится к выходной переменной, которая определяется на основе текущих и прошлых значений задержек.

Итог: ARIMA используется для того, чтобы модель максимально точно соответствовала специальной форме данных временных рядов.

Упражнение - построить модель ARIMA

Откройте папку /working в этом уроке и найдите файл notebook.ipynb.

Запустите блокнот, чтобы загрузить библиотеку statsmodels на Python; она вам понадобится для моделей ARIMA.
Загрузите необходимые библиотеки.

Теперь загрузите несколько дополнительных библиотек, полезных для построения графиков данных:

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape
from IPython.display import Image

%matplotlib inline
pd.options.display.float_format = '{:,.2f}'.format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore") # specify to ignore warning messages

Загрузите данные из файла /data/energy.csv в датафрейм Pandas и посмотрите на них:
```
energy = load_data('./data')[['load']]
energy.head(10)
```
Постройте график всех доступных данных по энергии с января 2012 года по декабрь 2014 года. Никаких сюрпризов быть не должно, так как мы видели эти данные на прошлом уроке:
```
energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Теперь давайте построим модель!

Создайте обучающие и тестовые наборы данных

Теперь ваши данные загружены, и вы можете разделить их на обучающий и тестовый наборы. Вы будете обучать свою модель на обучающем наборе. Как обычно, после завершения обучения модели вы оцените её точность с помощью тестового набора. Вам нужно убедиться, что тестовый набор охватывает более поздний период времени по сравнению с обучающим набором, чтобы гарантировать, что модель не получает информацию из будущих временных периодов.

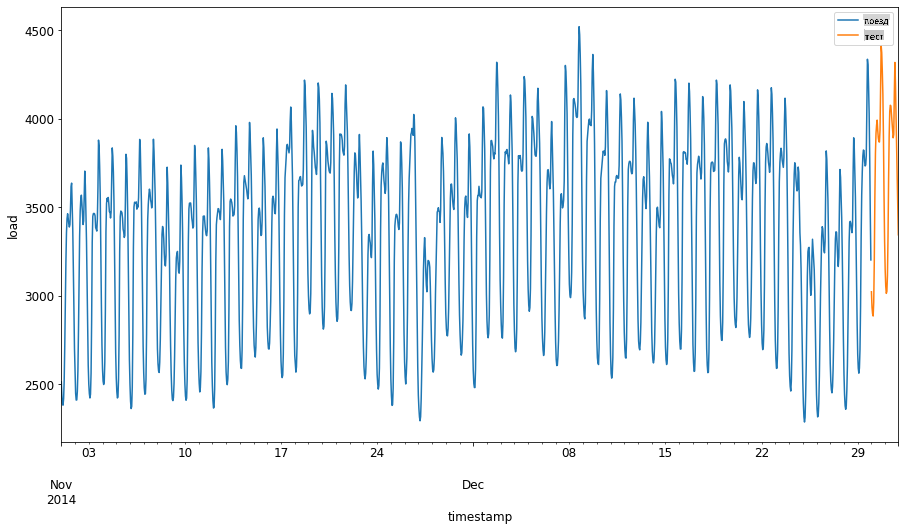
Отведите двухмесячный период с 1 сентября по 31 октября 2014 года для обучающего набора. Тестовый набор будет включать двухмесячный период с 1 ноября по 31 декабря 2014 года:
```
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
```
Поскольку эти данные отражают ежедневное потребление энергии, существует ярко выраженный сезонный паттерн, но потребление больше всего похоже на потребление в более недавние дни.
Визуализируйте различия:
```
energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Следовательно, использование относительно небольшого окна времени для обучения данных должно быть достаточным.

Примечание: Поскольку функция, которую мы используем для подгонки модели ARIMA, использует валидацию на обучающем наборе во время подгонки, мы опустим данные для валидации.

Подготовка данных для обучения

Теперь вам нужно подготовить данные для обучения, выполнив фильтрацию и масштабирование ваших данных. Отфильтруйте свой набор данных, чтобы включить только нужные временные периоды и столбцы, и масштабируйте данные, чтобы гарантировать, что они проецируются в интервале 0,1.

Отфильтруйте оригинальный набор данных, чтобы включить только вышеупомянутые временные периоды для каждого набора и только нужный столбец 'load' плюс дату:
```
train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)
```
Вы можете увидеть форму данных:
```
Training data shape:  (1416, 1)
Test data shape:  (48, 1)
```
Масштабируйте данные, чтобы они находились в диапазоне (0, 1).
```
scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
train.head(10)
```

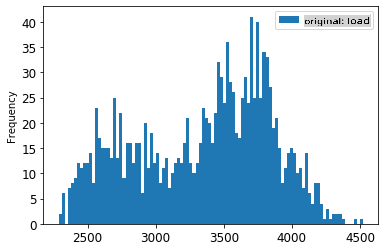
Визуализируйте оригинальные и масштабированные данные:

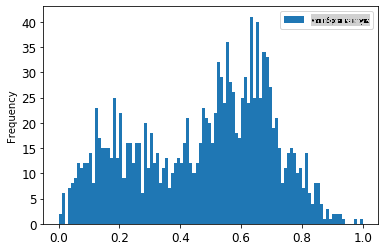
energy[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']].rename(columns={'load':'original load'}).plot.hist(bins=100, fontsize=12)
train.rename(columns={'load':'scaled load'}).plot.hist(bins=100, fontsize=12)
plt.show()

Оригинальные данные

Масштабированные данные

Теперь, когда вы откалибровали масштабированные данные, вы можете масштабировать тестовые данные:
```
test['load'] = scaler.transform(test)
test.head()
```

Реализация ARIMA

Пришло время реализовать ARIMA! Теперь вы будете использовать библиотеку statsmodels, которую вы установили ранее.

Теперь вам нужно выполнить несколько шагов

Определите модель, вызвав SARIMAX() and passing in the model parameters: p, d, and q parameters, and P, D, and Q parameters.
Prepare the model for the training data by calling the fit() function.
Make predictions calling the forecast() function and specifying the number of steps (the horizon) to forecast.

🎓 What are all these parameters for? In an ARIMA model there are 3 parameters that are used to help model the major aspects of a time series: seasonality, trend, and noise. These parameters are:

p: the parameter associated with the auto-regressive aspect of the model, which incorporates past values. d: the parameter associated with the integrated part of the model, which affects the amount of differencing (🎓 remember differencing 👆?) to apply to a time series. q: the parameter associated with the moving-average part of the model.

Note: If your data has a seasonal aspect - which this one does - , we use a seasonal ARIMA model (SARIMA). In that case you need to use another set of parameters: P, D, and Q which describe the same associations as p, d, and q, но соответствуйте сезонным компонентам модели.

Начните с установки желаемого значения горизонта. Давайте попробуем 3 часа:
```
# Specify the number of steps to forecast ahead
HORIZON = 3
print('Forecasting horizon:', HORIZON, 'hours')
```
Выбор лучших значений для параметров модели ARIMA может быть сложным, так как это довольно субъективно и требует много времени. Вы можете рассмотреть возможность использования библиотеки auto_arima() function from the pyramid,

Пока попробуйте некоторые ручные выборы, чтобы найти хорошую модель.

order = (4, 1, 0)
seasonal_order = (1, 1, 0, 24)

model = SARIMAX(endog=train, order=order, seasonal_order=seasonal_order)
results = model.fit()

print(results.summary())

Выводится таблица результатов.

Вы построили свою первую модель! Теперь нам нужно найти способ её оценить.

Оцените свою модель

Чтобы оценить вашу модель, вы можете выполнить так называемую валидацию walk forward. На практике модели временных рядов переобучаются каждый раз, когда появляются новые данные. Это позволяет модели делать наилучший прогноз на каждом временном шаге.

Начав с начала временного ряда, используя эту технику, обучите модель на обучающем наборе данных. Затем сделайте прогноз на следующий временной шаг. Прогноз оценивается по известному значению. Затем обучающий набор расширяется, чтобы включить известное значение, и процесс повторяется.

Примечание: Вы должны держать окно обучающего набора фиксированным для более эффективного обучения, так что каждый раз, когда вы добавляете новое наблюдение в обучающий набор, вы удаляете наблюдение из начала набора.

Этот процесс предоставляет более надежную оценку того, как модель будет работать на практике. Однако это требует вычислительных ресурсов для создания такого количества моделей. Это приемлемо, если данные небольшие или если модель проста, но может стать проблемой в больших масштабах.

Валидация walk-forward является золотым стандартом оценки моделей временных рядов и рекомендуется для ваших собственных проектов.

Сначала создайте тестовую точку данных для каждого шага HORIZON.

test_shifted = test.copy()

for t in range(1, HORIZON+1):
    test_shifted['load+'+str(t)] = test_shifted['load'].shift(-t, freq='H')

test_shifted = test_shifted.dropna(how='any')
test_shifted.head(5)

		load	load+1	load+2
2014-12-30	00:00:00	0.33	0.29	0.27
2014-12-30	01:00:00	0.29	0.27	0.27
2014-12-30	02:00:00	0.27	0.27	0.30
2014-12-30	03:00:00	0.27	0.30	0.41
2014-12-30	04:00:00	0.30	0.41	0.57

Данные сдвинуты горизонтально в соответствии с их горизонтом.

Сделайте прогнозы по вашим тестовым данным, используя этот подход скользящего окна в цикле, размер которого соответствует длине тестовых данных:

%%time
training_window = 720 # dedicate 30 days (720 hours) for training

train_ts = train['load']
test_ts = test_shifted

history = [x for x in train_ts]
history = history[(-training_window):]

predictions = list()

order = (2, 1, 0)
seasonal_order = (1, 1, 0, 24)

for t in range(test_ts.shape[0]):
    model = SARIMAX(endog=history, order=order, seasonal_order=seasonal_order)
    model_fit = model.fit()
    yhat = model_fit.forecast(steps = HORIZON)
    predictions.append(yhat)
    obs = list(test_ts.iloc[t])
    # move the training window
    history.append(obs[0])
    history.pop(0)
    print(test_ts.index[t])
    print(t+1, ': predicted =', yhat, 'expected =', obs)

Вы можете наблюдать за процессом обучения:

2014-12-30 00:00:00
1 : predicted = [0.32 0.29 0.28] expected = [0.32945389435989236, 0.2900626678603402, 0.2739480752014323]

2014-12-30 01:00:00
2 : predicted = [0.3  0.29 0.3 ] expected = [0.2900626678603402, 0.2739480752014323, 0.26812891674127126]

2014-12-30 02:00:00
3 : predicted = [0.27 0.28 0.32] expected = [0.2739480752014323, 0.26812891674127126, 0.3025962399283795]

Сравните прогнозы с фактической нагрузкой:

eval_df = pd.DataFrame(predictions, columns=['t+'+str(t) for t in range(1, HORIZON+1)])
eval_df['timestamp'] = test.index[0:len(test.index)-HORIZON+1]
eval_df = pd.melt(eval_df, id_vars='timestamp', value_name='prediction', var_name='h')
eval_df['actual'] = np.array(np.transpose(test_ts)).ravel()
eval_df[['prediction', 'actual']] = scaler.inverse_transform(eval_df[['prediction', 'actual']])
eval_df.head()

Вывод

		timestamp	h	prediction	actual
0	2014-12-30	00:00:00	t+1	3,008.74	3,023.00
1	2014-12-30	01:00:00	t+1	2,955.53	2,935.00
2	2014-12-30	02:00:00	t+1	2,900.17	2,899.00
3	2014-12-30	03:00:00	t+1	2,917.69	2,886.00
4	2014-12-30	04:00:00	t+1	2,946.99	2,963.00

Наблюдайте за прогнозами часовых данных по сравнению с фактической нагрузкой. Насколько это точно?

Проверьте точность модели

Проверьте точность вашей модели, протестировав её среднюю абсолютную процентную ошибку (MAPE) по всем прогнозам.

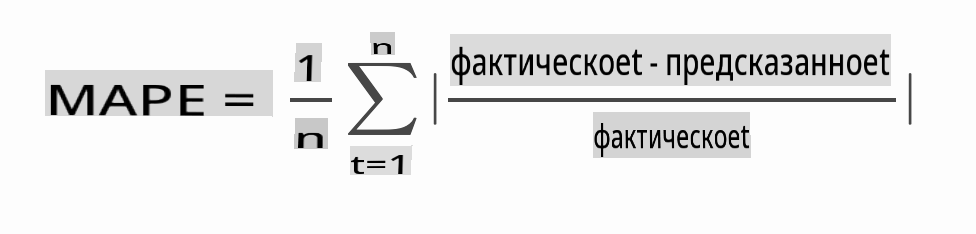
🧮 Покажите мне математику

MAPE используется для отображения точности прогнозирования как отношения, определённого вышеуказанной формулой. Разница между actual_t и predicted_t делится на actual_t. "Абсолютное значение в этом расчёте суммируется для каждой прогнозируемой точки во времени и делится на количество подогнанных точек n." wikipedia

Выразите уравнение в коде:

if(HORIZON > 1):
    eval_df['APE'] = (eval_df['prediction'] - eval_df['actual']).abs() / eval_df['actual']
    print(eval_df.groupby('h')['APE'].mean())

Рассчитайте MAPE для одного шага:

print('One step forecast MAPE: ', (mape(eval_df[eval_df['h'] == 't+1']['prediction'], eval_df[eval_df['h'] == 't+1']['actual']))*100, '%')

MAPE одного шага: 0.5570581332313952 %

Выведите MAPE многошагового прогноза:
```
print('Multi-step forecast MAPE: ', mape(eval_df['prediction'], eval_df['actual'])*100, '%')
```
```
Multi-step forecast MAPE:  1.1460048657704118 %
```
Чем ниже число, тем лучше: учитывайте, что прогноз с MAPE 10 отклоняется на 10%.

Но, как всегда, проще визуально увидеть такую оценку точности, так что давайте построим график:

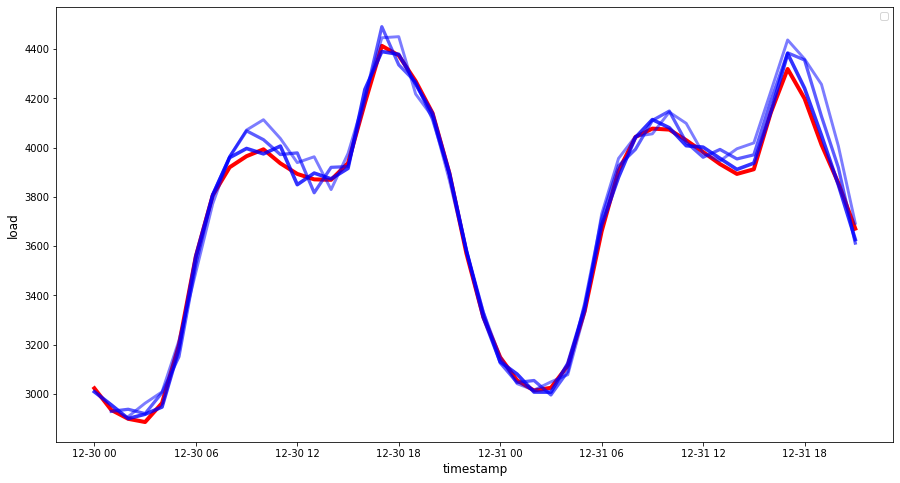
 if(HORIZON == 1):
    ## Plotting single step forecast
    eval_df.plot(x='timestamp', y=['actual', 'prediction'], style=['r', 'b'], figsize=(15, 8))

else:
    ## Plotting multi step forecast
    plot_df = eval_df[(eval_df.h=='t+1')][['timestamp', 'actual']]
    for t in range(1, HORIZON+1):
        plot_df['t+'+str(t)] = eval_df[(eval_df.h=='t+'+str(t))]['prediction'].values

    fig = plt.figure(figsize=(15, 8))
    ax = plt.plot(plot_df['timestamp'], plot_df['actual'], color='red', linewidth=4.0)
    ax = fig.add_subplot(111)
    for t in range(1, HORIZON+1):
        x = plot_df['timestamp'][(t-1):]
        y = plot_df['t+'+str(t)][0:len(x)]
        ax.plot(x, y, color='blue', linewidth=4*math.pow(.9,t), alpha=math.pow(0.8,t))

    ax.legend(loc='best')

plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

🏆 Очень красивый график, показывающий модель с хорошей точностью. Отличная работа!

🚀Задача

Изучите способы проверки точности модели временных рядов. Мы касаемся MAPE в этом уроке, но есть ли другие методы, которые вы могли бы использовать? Исследуйте их и сделайте пометки. Полезный документ можно найти здесь

Викторина после лекции

Обзор и самостоятельное изучение

Этот урок касается лишь основ прогнозирования временных рядов с помощью ARIMA. Найдите время, чтобы углубить свои знания, изучив этот репозиторий и его различные типы моделей, чтобы узнать другие способы построения моделей временных рядов.

Задание

Новая модель ARIMA

Отказ от ответственности:
Этот документ был переведен с использованием услуг машинного перевода на основе ИИ. Хотя мы стремимся к точности, пожалуйста, имейте в виду, что автоматические переводы могут содержать ошибки или неточности. Оригинальный документ на родном языке следует считать авторитетным источником. Для критически важной информации рекомендуется профессиональный человеческий перевод. Мы не несем ответственности за любые недоразумения или неправильные интерпретации, возникающие в результате использования этого перевода.

27 KiB Raw Permalink Blame History Unescape Escape