13 KiB

Raw Permalink Blame History

K-Means clustering

Quiz avant le cours

Dans cette leçon, vous apprendrez comment créer des clusters en utilisant Scikit-learn et le jeu de données de musique nigériane que vous avez importé plus tôt. Nous couvrirons les bases de K-Means pour le clustering. Gardez à l'esprit que, comme vous l'avez appris dans la leçon précédente, il existe de nombreuses façons de travailler avec des clusters et la méthode que vous utilisez dépend de vos données. Nous allons essayer K-Means car c'est la technique de clustering la plus courante. Commençons !

Termes que vous apprendrez :

Score de silhouette
Méthode du coude
Inertie
Variance

Introduction

K-Means Clustering est une méthode dérivée du domaine du traitement du signal. Elle est utilisée pour diviser et partitionner des groupes de données en 'k' clusters en utilisant une série d'observations. Chaque observation vise à regrouper un point de données donné le plus près de sa 'moyenne' la plus proche, ou le point central d'un cluster.

Les clusters peuvent être visualisés sous forme de diagrammes de Voronoi, qui incluent un point (ou 'graine') et sa région correspondante.

infographie par Jen Looper

Le processus de clustering K-Means s'exécute en trois étapes :

L'algorithme sélectionne un nombre k de points centraux en échantillonnant à partir du jeu de données. Après cela, il boucle :
1. Il assigne chaque échantillon au centroïde le plus proche.
2. Il crée de nouveaux centroïdes en prenant la valeur moyenne de tous les échantillons assignés aux centroïdes précédents.
3. Ensuite, il calcule la différence entre les nouveaux et anciens centroïdes et répète jusqu'à ce que les centroïdes soient stabilisés.

Un inconvénient de l'utilisation de K-Means est le fait que vous devrez établir 'k', c'est-à-dire le nombre de centroïdes. Heureusement, la 'méthode du coude' aide à estimer une bonne valeur de départ pour 'k'. Vous allez l'essayer dans un instant.

Prérequis

Vous travaillerez dans le fichier notebook.ipynb de cette leçon qui inclut l'importation des données et le nettoyage préliminaire que vous avez effectué dans la leçon précédente.

Exercice - préparation

Commencez par jeter un autre coup d'œil aux données des chansons.

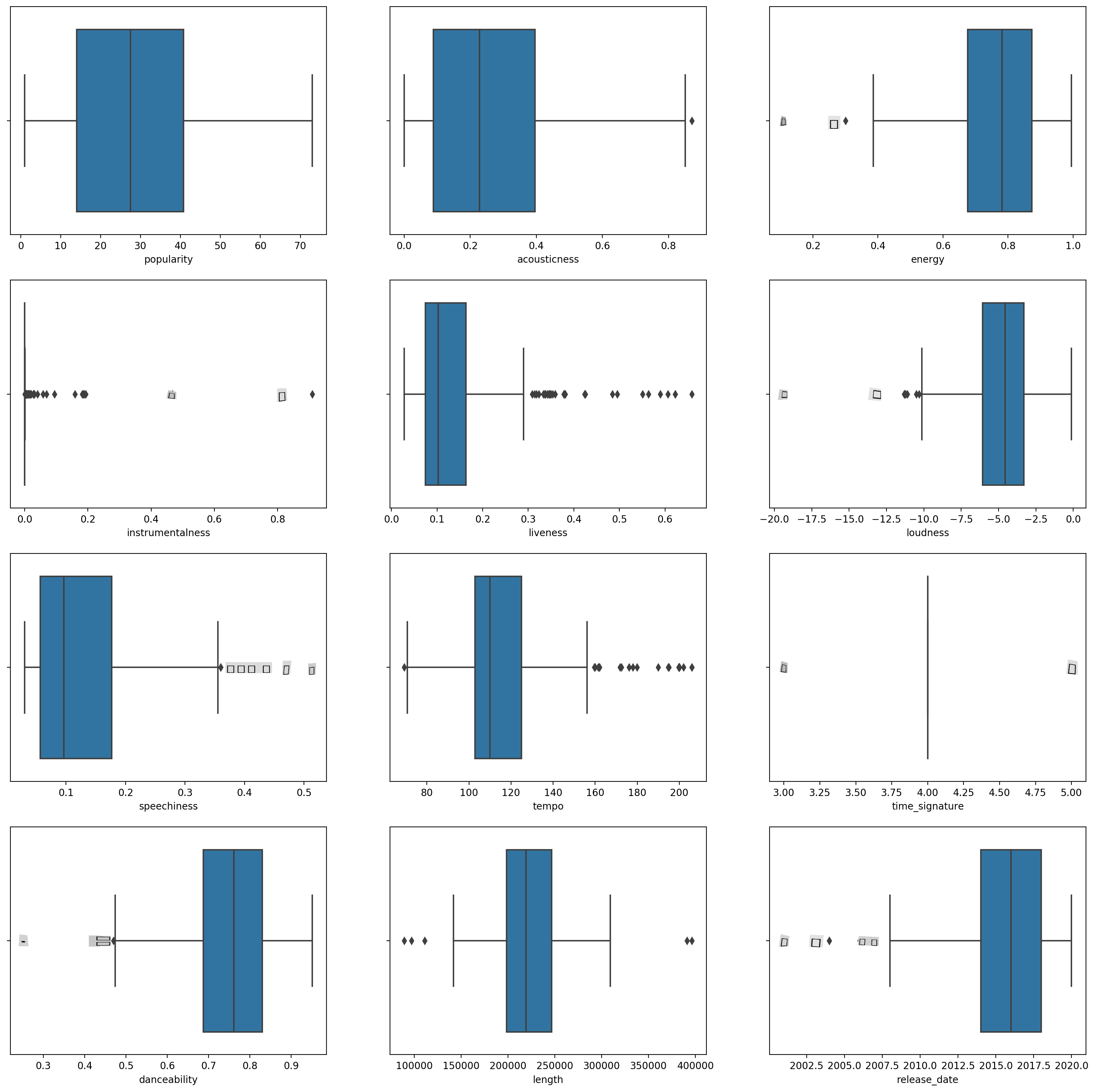
Créez un boxplot, en appelant boxplot() pour chaque colonne :

plt.figure(figsize=(20,20), dpi=200)

plt.subplot(4,3,1)
sns.boxplot(x = 'popularity', data = df)

plt.subplot(4,3,2)
sns.boxplot(x = 'acousticness', data = df)

plt.subplot(4,3,3)
sns.boxplot(x = 'energy', data = df)

plt.subplot(4,3,4)
sns.boxplot(x = 'instrumentalness', data = df)

plt.subplot(4,3,5)
sns.boxplot(x = 'liveness', data = df)

plt.subplot(4,3,6)
sns.boxplot(x = 'loudness', data = df)

plt.subplot(4,3,7)
sns.boxplot(x = 'speechiness', data = df)

plt.subplot(4,3,8)
sns.boxplot(x = 'tempo', data = df)

plt.subplot(4,3,9)
sns.boxplot(x = 'time_signature', data = df)

plt.subplot(4,3,10)
sns.boxplot(x = 'danceability', data = df)

plt.subplot(4,3,11)
sns.boxplot(x = 'length', data = df)

plt.subplot(4,3,12)
sns.boxplot(x = 'release_date', data = df)

Ces données sont un peu bruyantes : en observant chaque colonne sous forme de boxplot, vous pouvez voir des valeurs aberrantes.

Vous pourriez parcourir le jeu de données et supprimer ces valeurs aberrantes, mais cela rendrait les données plutôt minimales.

Pour l'instant, choisissez les colonnes que vous utiliserez pour votre exercice de clustering. Choisissez celles avec des plages similaires et encodez la colonne artist_top_genre en tant que données numériques :

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()

X = df.loc[:, ('artist_top_genre','popularity','danceability','acousticness','loudness','energy')]

y = df['artist_top_genre']

X['artist_top_genre'] = le.fit_transform(X['artist_top_genre'])

y = le.transform(y)

Maintenant, vous devez choisir combien de clusters cibler. Vous savez qu'il y a 3 genres musicaux que nous avons extraits du jeu de données, alors essayons 3 :

from sklearn.cluster import KMeans

nclusters = 3 
seed = 0

km = KMeans(n_clusters=nclusters, random_state=seed)
km.fit(X)

# Predict the cluster for each data point

y_cluster_kmeans = km.predict(X)
y_cluster_kmeans

Vous voyez un tableau imprimé avec des clusters prévus (0, 1 ou 2) pour chaque ligne du dataframe.

Utilisez ce tableau pour calculer un 'score de silhouette' :

from sklearn import metrics
score = metrics.silhouette_score(X, y_cluster_kmeans)
score

Score de silhouette

Recherchez un score de silhouette plus proche de 1. Ce score varie de -1 à 1, et si le score est 1, le cluster est dense et bien séparé des autres clusters. Une valeur proche de 0 représente des clusters qui se chevauchent avec des échantillons très proches de la frontière de décision des clusters voisins. (Source)

Notre score est .53, donc juste au milieu. Cela indique que nos données ne sont pas particulièrement bien adaptées à ce type de clustering, mais continuons.

Exercice - construire un modèle

Importez KMeans et commencez le processus de clustering.
```
from sklearn.cluster import KMeans
wcss = []

for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)
```
Il y a quelques parties ici qui méritent d'être expliquées.

🎓 range : Ce sont les itérations du processus de clustering

🎓 random_state : "Détermine la génération de nombres aléatoires pour l'initialisation des centroïdes." Source

🎓 WCSS : "somme des carrés à l'intérieur des clusters" mesure la distance moyenne au carré de tous les points au sein d'un cluster par rapport au centroïde du cluster. Source.

🎓 Inertie : Les algorithmes K-Means tentent de choisir des centroïdes pour minimiser 'l'inertie', "une mesure de la cohérence interne des clusters." Source. La valeur est ajoutée à la variable wcss à chaque itération.

🎓 k-means++ : Dans Scikit-learn, vous pouvez utiliser l'optimisation 'k-means++', qui "initialise les centroïdes pour être (généralement) éloignés les uns des autres, ce qui conduit probablement à de meilleurs résultats qu'une initialisation aléatoire."

Méthode du coude

Auparavant, vous avez supposé que, parce que vous avez ciblé 3 genres musicaux, vous devriez choisir 3 clusters. Mais est-ce vraiment le cas ?

Utilisez la 'méthode du coude' pour vous en assurer.
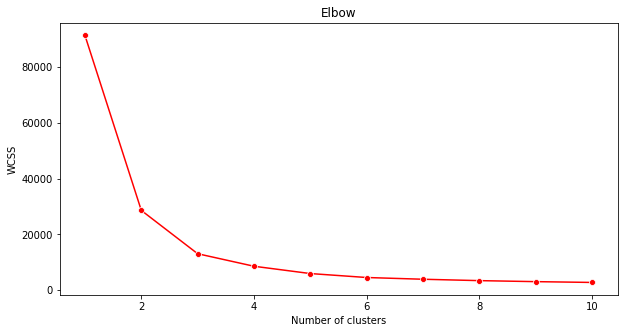
```
plt.figure(figsize=(10,5))
sns.lineplot(x=range(1, 11), y=wcss, marker='o', color='red')
plt.title('Elbow')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
```
Utilisez la variable wcss que vous avez construite à l'étape précédente pour créer un graphique montrant où se trouve la 'flexion' dans le coude, ce qui indique le nombre optimal de clusters. Peut-être que c'est 3 !

Exercice - afficher les clusters

Essayez à nouveau le processus, cette fois en définissant trois clusters, et affichez les clusters sous forme de nuage de points :

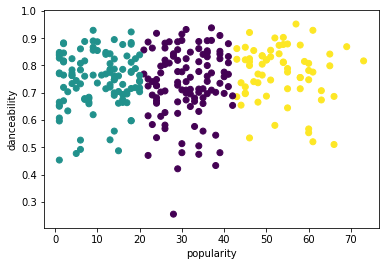
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
labels = kmeans.predict(X)
plt.scatter(df['popularity'],df['danceability'],c = labels)
plt.xlabel('popularity')
plt.ylabel('danceability')
plt.show()

Vérifiez l'exactitude du modèle :
```
labels = kmeans.labels_

correct_labels = sum(y == labels)

print("Result: %d out of %d samples were correctly labeled." % (correct_labels, y.size))

print('Accuracy score: {0:0.2f}'. format(correct_labels/float(y.size)))
```
L'exactitude de ce modèle n'est pas très bonne, et la forme des clusters vous donne un indice sur la raison.

Ces données sont trop déséquilibrées, trop peu corrélées et il y a trop de variance entre les valeurs des colonnes pour bien se regrouper. En fait, les clusters qui se forment sont probablement fortement influencés ou biaisés par les trois catégories de genre que nous avons définies ci-dessus. Cela a été un processus d'apprentissage !

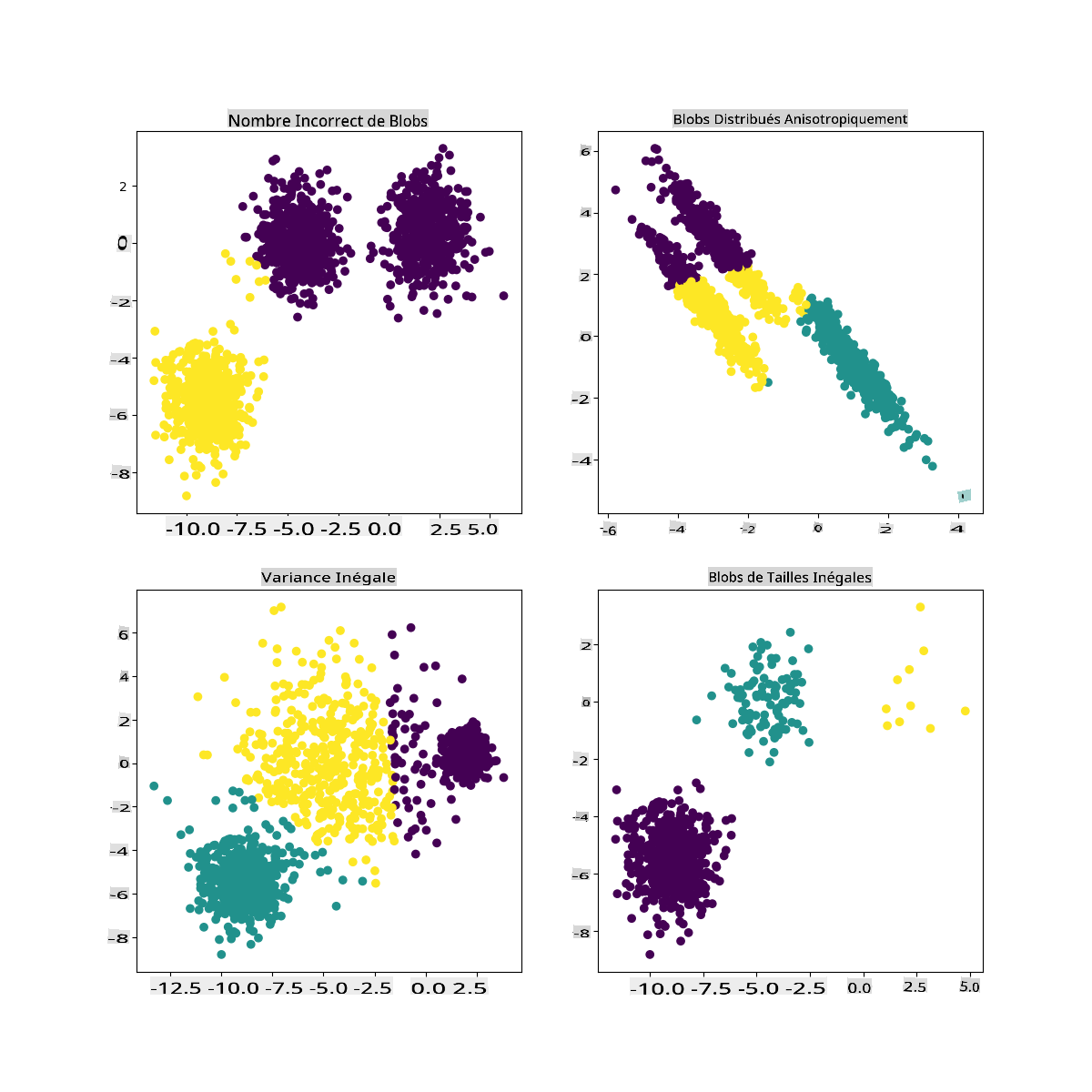
Dans la documentation de Scikit-learn, vous pouvez voir qu'un modèle comme celui-ci, avec des clusters pas très bien démarqués, a un problème de 'variance' :

Infographie de Scikit-learn

Variance

La variance est définie comme "la moyenne des différences au carré par rapport à la moyenne" (Source). Dans le contexte de ce problème de clustering, cela fait référence aux données dont les nombres de notre jeu de données tendent à diverger un peu trop de la moyenne.

✅ C'est un excellent moment pour réfléchir à toutes les manières dont vous pourriez corriger ce problème. Ajuster un peu plus les données ? Utiliser d'autres colonnes ? Utiliser un algorithme différent ? Indice : Essayez de normaliser vos données et testez d'autres colonnes.

Essayez ce 'calculateur de variance' pour mieux comprendre le concept.

🚀Défi

Passez du temps avec ce notebook, en ajustant les paramètres. Pouvez-vous améliorer l'exactitude du modèle en nettoyant davantage les données (en supprimant les valeurs aberrantes, par exemple) ? Vous pouvez utiliser des poids pour donner plus de poids à certains échantillons de données. Que pouvez-vous faire d'autre pour créer de meilleurs clusters ?

Indice : Essayez de normaliser vos données. Il y a du code commenté dans le notebook qui ajoute une normalisation standard pour que les colonnes de données se ressemblent davantage en termes de plage. Vous constaterez que, bien que le score de silhouette diminue, la 'flexion' dans le graphique du coude s'adoucit. Cela est dû au fait que laisser les données non normalisées permet aux données avec moins de variance de porter plus de poids. Lisez un peu plus sur ce problème ici.

Quiz après le cours

Révision & Auto-apprentissage

Jetez un œil à un simulateur K-Means comme celui-ci. Vous pouvez utiliser cet outil pour visualiser des points de données d'exemple et déterminer ses centroïdes. Vous pouvez modifier l'aléatoire des données, le nombre de clusters et le nombre de centroïdes. Cela vous aide-t-il à comprendre comment les données peuvent être regroupées ?

De plus, jetez un œil à ce document sur K-Means de Stanford.

Devoir

Essayez différentes méthodes de clustering

Avertissement :
Ce document a été traduit à l'aide de services de traduction automatique basés sur l'IA. Bien que nous nous efforçons d'assurer l'exactitude, veuillez noter que les traductions automatiques peuvent contenir des erreurs ou des inexactitudes. Le document original dans sa langue native doit être considéré comme la source autoritaire. Pour des informations critiques, une traduction humaine professionnelle est recommandée. Nous ne sommes pas responsables des malentendus ou des interprétations erronées découlant de l'utilisation de cette traduction.

13 KiB Raw Permalink Blame History