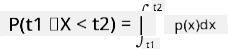38 KiB

Raw Permalink Blame History Unescape Escape

Кратак увод у статистику и вероватноћу


Статистика и вероватноћа - Скетч од @nitya

Теорија статистике и вероватноће су две блиско повезане области математике које су веома значајне за науку о подацима. Могуће је радити са подацима без дубоког познавања математике, али је ипак боље знати барем основне концепте. Овде ћемо представити кратак увод који ће вам помоћи да започнете.

Квиз пре предавања

Вероватноћа и случајне променљиве

Вероватноћа је број између 0 и 1 који изражава колико је неки догађај вероватан. Дефинише се као број позитивних исхода (који воде до догађаја), подељен укупним бројем исхода, под условом да су сви исходи једнако вероватни. На пример, када бацимо коцку, вероватноћа да добијемо паран број је 3/6 = 0.5.

Када говоримо о догађајима, користимо случајне променљиве. На пример, случајна променљива која представља број добијен бацањем коцке може имати вредности од 1 до 6. Скуп бројева од 1 до 6 назива се простор узорка. Можемо говорити о вероватноћи да случајна променљива има одређену вредност, на пример P(X=3)=1/6.

Случајна променљива у претходном примеру назива се дискретна, јер има пребројив простор узорка, односно постоје одвојене вредности које се могу набројати. Постоје случајеви када је простор узорка опсег реалних бројева или цео скуп реалних бројева. Такве променљиве називају се континуалне. Добар пример је време доласка аутобуса.

Расподела вероватноће

У случају дискретних случајних променљивих, лако је описати вероватноћу сваког догађаја функцијом P(X). За сваку вредност s из простора узорка S она ће дати број између 0 и 1, тако да збир свих вредности P(X=s) за све догађаје буде 1.

Најпознатија дискретна расподела је равномерна расподела, у којој постоји простор узорка од N елемената, са једнаком вероватноћом од 1/N за сваки од њих.

Теже је описати расподелу вероватноће континуалне променљиве, са вредностима из неког интервала [a,b], или целог скупа реалних бројева ℝ. Размотрите случај времена доласка аутобуса. У ствари, за свако тачно време доласка t, вероватноћа да аутобус стигне баш у то време је 0!

Сада знате да се догађаји са вероватноћом 0 дешавају, и то веома често! Барем сваки пут када аутобус стигне!

Можемо говорити само о вероватноћи да променљива падне у дати интервал вредности, нпр. P(t₁≤X<t₂). У овом случају, расподела вероватноће описује се функцијом густине вероватноће p(x), тако да

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Континуални аналог равномерне расподеле назива се континуална равномерна, која је дефинисана на коначном интервалу. Вероватноћа да вредност X падне у интервал дужине l је пропорционална l, и расте до 1.

Још једна важна расподела је нормална расподела, о којој ћемо детаљније говорити у наставку.

Средња вредност, варијанса и стандардна девијација

Претпоставимо да узимамо низ од n узорака случајне променљиве X: x₁, x₂, ..., x_n. Можемо дефинисати средњу вредност (или аритметичку средину) низа на традиционалан начин као (x₁+x₂+x_n)/n. Како повећавамо величину узорка (тј. узимамо границу са n→∞), добијамо средњу вредност (која се назива и очекивање) расподеле. Очекивање ћемо означити са E(x).

Може се показати да за било коју дискретну расподелу са вредностима {x₁, x₂, ..., x_N} и одговарајућим вероватноћама p₁, p₂, ..., p_N, очекивање ће бити E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Да бисмо идентификовали колико су вредности распршене, можемо израчунати варијансу σ² = ∑(x_i - μ)²/n, где је μ средња вредност низа. Вредност σ назива се стандардна девијација, а σ² назива се варијанса.

Мода, медијана и квартили

Понекад средња вредност не представља адекватно "типичну" вредност за податке. На пример, када постоји неколико екстремних вредности које су потпуно ван опсега, оне могу утицати на средњу вредност. Још један добар показатељ је медијана, вредност таква да је половина података мања од ње, а друга половина - већа.

Да бисмо боље разумели расподелу података, корисно је говорити о квартилима:

Први квартил, или Q1, је вредност таква да 25% података пада испод ње
Трећи квартил, или Q3, је вредност таква да 75% података пада испод ње

Графички можемо представити однос између медијане и квартила у дијаграму који се назива бокс плот:

Овде такође израчунавамо интерквартилни опсег IQR=Q3-Q1, и такозване изузетке - вредности које леже ван граница [Q1-1.5IQR,Q3+1.5IQR].

За коначну расподелу која садржи мали број могућих вредности, добра "типична" вредност је она која се најчешће појављује, а назива се мода. Често се примењује на категоријске податке, као што су боје. Размотрите ситуацију када имамо две групе људи - једну која снажно преферира црвену боју, и другу која преферира плаву. Ако боје кодирамо бројевима, средња вредност за омиљену боју била би негде у спектру наранџасто-зелене, што не указује на стварну преференцију ниједне групе. Међутим, мода би била или једна од боја, или обе боје, ако је број људи који гласају за њих једнак (у том случају узорак називамо мултимодалним).

Подаци из стварног света

Када анализирамо податке из стварног живота, они често нису случајне променљиве у правом смислу, у смислу да не изводимо експерименте са непознатим резултатом. На пример, размотрите тим бејзбол играча и њихове телесне податке, као што су висина, тежина и старост. Ти бројеви нису баш случајни, али можемо применити исте математичке концепте. На пример, низ тежина људи може се сматрати низом вредности извучених из неке случајне променљиве. Испод је низ тежина стварних бејзбол играча из Мејџор лиге бејзбола, узет из овог скупа података (ради ваше удобности, приказане су само прве 20 вредности):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Напомена: Да бисте видели пример рада са овим скупом података, погледајте пратећу свеску. Такође постоји низ изазова кроз ову лекцију, и можете их завршити додавањем неког кода у ту свеску. Ако нисте сигурни како да радите са подацима, не брините - вратићемо се раду са подацима користећи Python касније. Ако не знате како да извршите код у Jupyter Notebook-у, погледајте овај чланак.

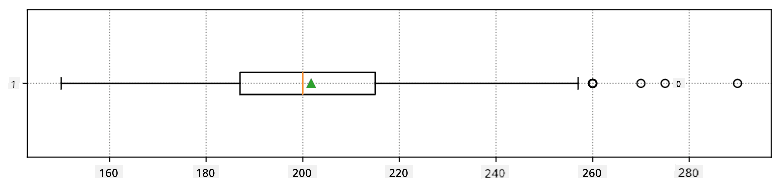
Ево бокс плота који приказује средњу вредност, медијану и квартиле за наше податке:

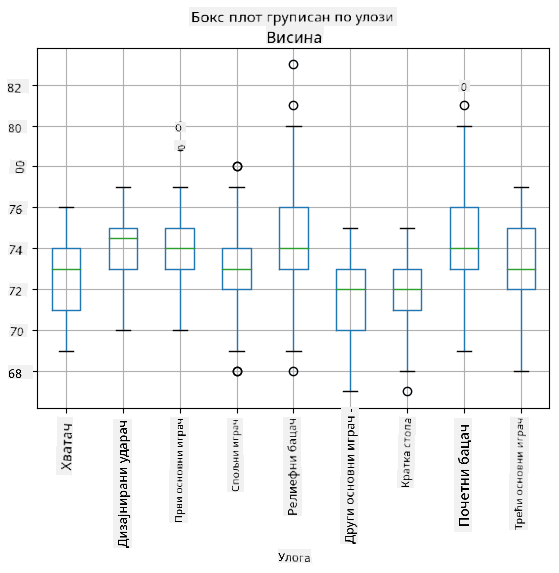
Пошто наши подаци садрже информације о различитим улогама играча, можемо направити бокс плот по улогама - то ће нам омогућити да добијемо идеју о томе како се вредности параметара разликују у зависности од улога. Овог пута ћемо размотрити висину:

Овај дијаграм сугерише да је, у просеку, висина играча на првој бази већа од висине играча на другој бази. Касније у овој лекцији научићемо како можемо формалније тестирати ову хипотезу и како да покажемо да су наши подаци статистички значајни за то.

Када радимо са подацима из стварног света, претпостављамо да су сви подаци узорци извучени из неке расподеле вероватноће. Ова претпоставка нам омогућава да применимо технике машинског учења и изградимо функционалне предиктивне моделе.

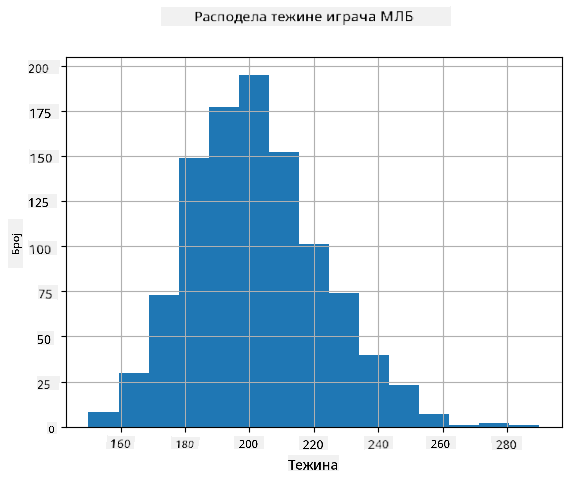
Да бисмо видели каква је расподела наших података, можемо нацртати график који се назива хистограм. Оса X би садржала број различитих интервала тежине (такозваних бинова), а вертикална оса би показивала број пута када је узорак наше случајне променљиве био у датом интервалу.

Из овог хистограма можете видети да су све вредности концентрисане око одређене средње тежине, и што се више удаљавамо од те тежине - мање тежина те вредности се сусреће. Односно, веома је мало вероватно да ће тежина бејзбол играча бити веома различита од средње тежине. Варијанса тежина показује степен до којег тежине могу да се разликују од средње вредности.

Ако узмемо тежине других људи, не из бејзбол лиге, расподела ће вероватно бити другачија. Међутим, облик расподеле ће бити исти, али средња вредност и варијанса ће се променити. Дакле, ако обучимо наш модел на бејзбол играчима, вероватно ће давати погрешне резултате када се примени на студенте универзитета, јер је основна расподела другачија.

Нормална расподела

Расподела тежина коју смо видели изнад је веома типична, и многе мере из стварног света следе исти тип расподеле, али са различитом средњом вредношћу и варијансом. Ова расподела назива се нормална расподела, и она игра веома важну улогу у статистици.

Коришћење нормалне расподеле је исправан начин за генерисање случајних тежина потенцијалних бејзбол играча. Када знамо средњу тежину mean и стандардну девијацију std, можемо генерисати 1000 узорака тежине на следећи начин:

samples = np.random.normal(mean,std,1000)

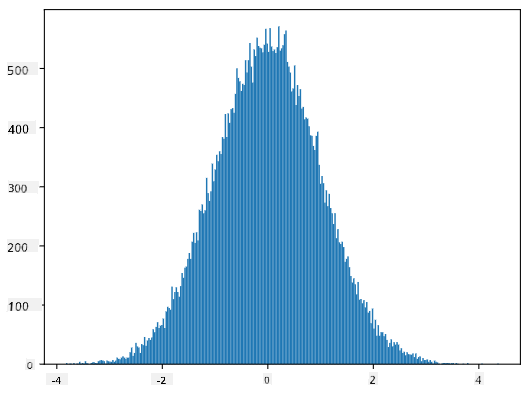
Ако нацртамо хистограм генерисаних узорака, видећемо слику веома сличну оној приказаној изнад. А ако повећамо број узорака и број бинова, можемо генерисати слику нормалне расподеле која је ближа идеалу:

Нормална расподела са mean=0 и std.dev=1

Интервали поверења

Када говоримо о тежинама бејзбол играча, претпостављамо да постоји одређена случајна променљива W која одговара идеалној расподели вероватноће тежина свих бејзбол играча (такозвана популација). Наш низ тежина одговара подскупу свих бејзбол играча који називамо узорак. Занимљиво питање је, можемо ли знати параметре расподеле W, односно средњу вредност и варијансу популације?

Најлакши одговор био би израчунати средњу вредност и варијансу нашег узорка. Међутим, могло би се десити да наш случајни узорак не представља тачно целу популацију. Због тога има смисла говорити о интервалу поверења.

Интервал поверења је процена стварне средње вредности популације на основу нашег узорка, која је тачна са одређеном вероватноћом (или нивом поверења).

Претпоставимо да имамо узорак X

1, ..., X_n из наше дистрибуције. Сваки пут када узмемо узорак из наше дистрибуције, добијамо различиту вредност средње вредности μ. Због тога се μ може сматрати случајном променљивом. Интервал поверења са поверењем p је пар вредности (L_p,R_p), тако да P(L_p≤μ≤R_p) = p, односно вероватноћа да измерена средња вредност падне у интервал једнака је p.

Прелази границе нашег кратког увода да бисмо детаљно објаснили како се ти интервали поверења израчунавају. Више детаља можете пронаћи на Википедији. Укратко, дефинишемо дистрибуцију израчунате средње вредности узорка у односу на праву средњу вредност популације, што се назива Студентова дистрибуција.

Занимљива чињеница: Студентова дистрибуција је добила име по математичару Вилијаму Силију Госету, који је објавио свој рад под псеудонимом "Студент". Радио је у пивари Гинис, и, према једној верзији, његов послодавац није желео да јавност зна да користе статистичке тестове за одређивање квалитета сировина.

Ако желимо да проценимо средњу вредност μ наше популације са поверењем p, потребно је да узмемо (1-p)/2-ти проценат Студентове дистрибуције A, који се може узети из табела или израчунати помоћу уграђених функција статистичког софтвера (нпр. Python, R, итд.). Тада би интервал за μ био дат са X±A*D/√n, где је X добијена средња вредност узорка, а D је стандардна девијација.

Напомена: Такође изостављамо дискусију о важном концепту степени слободе, који је важан у односу на Студентову дистрибуцију. Можете се обратити потпунијим књигама о статистици да бисте дубље разумели овај концепт.

Пример израчунавања интервала поверења за тежине и висине дат је у пратећим нотебуцима.

p	Средња тежина
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Приметите да што је већа вероватноћа поверења, то је шири интервал поверења.

Тестирање хипотеза

У нашем скупу података о бејзбол играчима постоје различите улоге играча, које се могу сумирати у табели испод (погледајте пратећи нотебук да видите како се ова табела може израчунати):

Улога	Висина	Тежина	Број
Ловач	72.723684	204.328947	76
Дизајнирани ударач	74.222222	220.888889	18
Први базмен	74.000000	213.109091	55
Спољни играч	73.010309	199.113402	194
Релиефни бацач	74.374603	203.517460	315
Други базмен	71.362069	184.344828	58
Шортстоп	71.903846	182.923077	52
Почетни бацач	74.719457	205.163636	221
Трећи базмен	73.044444	200.955556	45

Можемо приметити да је просечна висина првих базмена већа од оне код других базмена. Због тога можемо бити у искушењу да закључимо да су први базмени виши од других базмена.

Ова изјава се назива хипотеза, јер не знамо да ли је чињеница заиста тачна или не.

Међутим, није увек очигледно да ли можемо донети овај закључак. Из горње дискусије знамо да свака средња вредност има повезан интервал поверења, и стога ова разлика може бити само статистичка грешка. Потребан нам је формалнији начин да тестирамо нашу хипотезу.

Хајде да израчунамо интервале поверења одвојено за висине првих и других базмена:

Поверење	Први базмени	Други базмени
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Можемо видети да се ни под једним поверењем интервали не преклапају. То доказује нашу хипотезу да су први базмени виши од других базмена.

Формалније, проблем који решавамо је да видимо да ли су две дистрибуције вероватноће исте, или барем имају исте параметре. У зависности од дистрибуције, потребно је да користимо различите тестове за то. Ако знамо да су наше дистрибуције нормалне, можемо применити Студентов t-тест.

У Студентовом t-тесту израчунавамо такозвану t-вредност, која указује на разлику између средњих вредности, узимајући у обзир варијансу. Показано је да t-вредност прати Студентову дистрибуцију, што нам омогућава да добијемо граничну вредност за дати ниво поверења p (ово се може израчунати или пронаћи у нумеричким табелама). Затим упоређујемо t-вредност са овом граничном вредношћу да бисмо одобрили или одбацили хипотезу.

У Python-у можемо користити пакет SciPy, који укључује функцију ttest_ind (поред многих других корисних статистичких функција!). Она израчунава t-вредност за нас, а такође ради обрнуто претраживање p-вредности поверења, тако да можемо само погледати поверење да бисмо донели закључак.

На пример, наше поређење висина првих и других базмена даје нам следеће резултате:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

У нашем случају, p-вредност је веома ниска, што значи да постоје снажни докази који подржавају да су први базмени виши.

Постоје и различите друге врсте хипотеза које бисмо могли тестирати, на пример:

Да докажемо да дати узорак прати неку дистрибуцију. У нашем случају претпоставили смо да су висине нормално распоређене, али то захтева формалну статистичку верификацију.
Да докажемо да средња вредност узорка одговара некој унапред дефинисаној вредности
Да упоредимо средње вредности више узорака (нпр. која је разлика у нивоу среће међу различитим старосним групама)

Закон великих бројева и Централна гранична теорема

Један од разлога зашто је нормална дистрибуција толико важна је такозвана централна гранична теорема. Претпоставимо да имамо велики узорак независних N вредности X₁, ..., X_N, узоркованих из било које дистрибуције са средњом вредношћу μ и варијансом σ². Тада, за довољно велики N (другим речима, када N→∞), средња вредност Σ_iX_i биће нормално распоређена, са средњом вредношћу μ и варијансом σ²/N.

Други начин да интерпретирамо централну граничну теорему је да кажемо да без обзира на дистрибуцију, када израчунате средњу вредност збира било којих случајних вредности, добијате нормалну дистрибуцију.

Из централне граничне теореме такође следи да, када N→∞, вероватноћа да средња вредност узорка буде једнака μ постаје 1. Ово је познато као закон великих бројева.

Коваријанса и корелација

Једна од ствари коју наука о подацима ради је проналажење односа између података. Кажемо да се две секвенце корелишу када показују слично понашање у исто време, односно или истовремено расту/опадају, или једна секвенца расте када друга опада и обрнуто. Другим речима, чини се да постоји нека веза између две секвенце.

Корелација не мора нужно указивати на узрочну везу између две секвенце; понекад обе променљиве могу зависити од неког спољашњег узрока, или може бити чиста случајност да се две секвенце корелишу. Међутим, јака математичка корелација је добар показатељ да су две променљиве на неки начин повезане.

Математички, главни концепт који показује однос између две случајне променљиве је коваријанса, која се израчунава овако: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Израчунавамо одступање обе променљиве од њихових средњих вредности, а затим производ тих одступања. Ако обе променљиве одступају заједно, производ ће увек бити позитивна вредност, која ће се сабирати у позитивну коваријансу. Ако обе променљиве одступају неусклађено (тј. једна пада испод просека када друга расте изнад просека), увек ћемо добити негативне бројеве, који ће се сабирати у негативну коваријансу. Ако одступања нису зависна, сабираће се приближно на нулу.

Апсолутна вредност коваријансе нам не говори много о томе колика је корелација, јер зависи од величине стварних вредности. Да бисмо је нормализовали, можемо поделити коваријансу са стандардном девијацијом обе променљиве, да бисмо добили корелацију. Добра ствар је што је корелација увек у опсегу [-1,1], где 1 указује на јаку позитивну корелацију између вредности, -1 - јаку негативну корелацију, а 0 - никакву корелацију (променљиве су независне).

Пример: Можемо израчунати корелацију између тежина и висина бејзбол играча из горе поменутог скупа података:

print(np.corrcoef(weights,heights))

Као резултат добијамо матрицу корелације попут ове:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Матрица корелације C може се израчунати за било који број улазних секвенци S₁, ..., S_n. Вредност C_ij је корелација између S_i и S_j, а дијагонални елементи су увек 1 (што је такође само-корелација S_i).

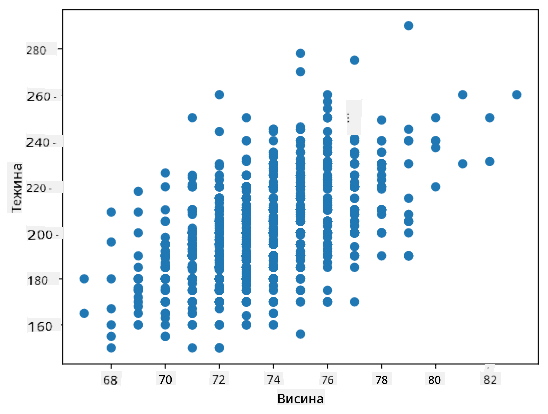
У нашем случају, вредност 0.53 указује да постоји нека корелација између тежине и висине особе. Такође можемо направити график расејања једне вредности у односу на другу да бисмо визуелно видели однос:

Више примера корелације и коваријансе можете пронаћи у пратећем нотебуку.

Закључак

У овом одељку смо научили:

основна статистичка својства података, као што су средња вредност, варијанса, модус и квартили
различите дистрибуције случајних променљивих, укључујући нормалну дистрибуцију
како пронаћи корелацију између различитих својстава
како користити звучни апарат математике и статистике да бисмо доказали неке хипотезе
како израчунати интервале поверења за случајну променљиву на основу узорка података

Иако ово дефинитивно није исцрпан списак тема које постоје у оквиру вероватноће и статистике, требало би да буде довољно да вам пружи добар почетак у овом курсу.

🚀 Изазов

Користите пример кода у нотебуку да тестирате друге хипотезе:

Први базмени су старији од других базмена
Први базмени су виши од трећих базмена
Шортстопови су виши од других базмена

Квиз након предавања

Преглед и самостално учење

Вероватноћа и статистика су толико широка тема да заслужују свој курс. Ако сте заинтересовани да дубље уђете у теорију, можда ћете желети да наставите са читањем неких од следећих књига:

Карлос Фернандез-Гранда са Њујоршког универзитета има одличне белешке са предавања Вероватноћа и статистика за науку о подацима (доступно онлајн)
Питер и Ендру Брус. Практична статистика за научнике о подацима. [пример кода у R].
Џејмс Д. Милер. Статистика за науку о подацима [пример кода у R]

Задатак

Мала студија о дијабетесу

Кредити

Ово предавање је написано са ♥️ од стране Дмитрија Сошњикова

Одрицање од одговорности:
Овај документ је преведен коришћењем услуге за превођење помоћу вештачке интелигенције Co-op Translator. Иако тежимо тачности, молимо вас да имате у виду да аутоматски преводи могу садржати грешке или нетачности. Оригинални документ на изворном језику треба сматрати ауторитативним извором. За критичне информације препоручује се професионални превод од стране људи. Не сносимо одговорност за било каква погрешна тумачења или неспоразуме који могу произаћи из коришћења овог превода.

38 KiB Raw Permalink Blame History Unescape Escape