30 KiB

Raw Permalink Blame History Unescape Escape

Giới thiệu Ngắn gọn về Thống kê và Xác suất


Thống kê và Xác suất - Sketchnote bởi @nitya

Lý thuyết Thống kê và Xác suất là hai lĩnh vực liên quan chặt chẽ trong Toán học và rất quan trọng đối với Khoa học Dữ liệu. Bạn có thể làm việc với dữ liệu mà không cần kiến thức sâu về toán học, nhưng vẫn tốt hơn nếu biết ít nhất một số khái niệm cơ bản. Dưới đây là một phần giới thiệu ngắn gọn để giúp bạn bắt đầu.

Câu hỏi trước bài giảng

Xác suất và Biến ngẫu nhiên

Xác suất là một số nằm trong khoảng từ 0 đến 1, biểu thị mức độ khả năng xảy ra của một sự kiện. Nó được định nghĩa là số kết quả tích cực (dẫn đến sự kiện), chia cho tổng số kết quả, với điều kiện tất cả các kết quả đều có khả năng xảy ra như nhau. Ví dụ, khi chúng ta tung một con xúc xắc, xác suất để có được một số chẵn là 3/6 = 0.5.

Khi nói về các sự kiện, chúng ta sử dụng biến ngẫu nhiên. Ví dụ, biến ngẫu nhiên đại diện cho số nhận được khi tung xúc xắc sẽ có giá trị từ 1 đến 6. Tập hợp các số từ 1 đến 6 được gọi là không gian mẫu. Chúng ta có thể nói về xác suất của một biến ngẫu nhiên nhận một giá trị nhất định, ví dụ P(X=3)=1/6.

Biến ngẫu nhiên trong ví dụ trước được gọi là rời rạc, vì nó có không gian mẫu đếm được, tức là có các giá trị riêng biệt có thể liệt kê. Có những trường hợp không gian mẫu là một khoảng số thực, hoặc toàn bộ tập hợp số thực. Những biến như vậy được gọi là liên tục. Một ví dụ điển hình là thời gian xe buýt đến.

Phân phối Xác suất

Trong trường hợp biến ngẫu nhiên rời rạc, rất dễ mô tả xác suất của mỗi sự kiện bằng một hàm P(X). Đối với mỗi giá trị s từ không gian mẫu S, hàm sẽ trả về một số từ 0 đến 1, sao cho tổng tất cả các giá trị của P(X=s) cho tất cả các sự kiện bằng 1.

Phân phối rời rạc nổi tiếng nhất là phân phối đồng đều, trong đó có một không gian mẫu gồm N phần tử, với xác suất bằng nhau là 1/N cho mỗi phần tử.

Mô tả phân phối xác suất của một biến liên tục khó hơn, với các giá trị được lấy từ một khoảng [a,b], hoặc toàn bộ tập hợp số thực ℝ. Hãy xem xét trường hợp thời gian xe buýt đến. Thực tế, đối với mỗi thời gian đến chính xác t, xác suất xe buýt đến đúng thời điểm đó là 0!

Bây giờ bạn đã biết rằng các sự kiện có xác suất bằng 0 vẫn xảy ra, và rất thường xuyên! Ít nhất là mỗi lần xe buýt đến!

Chúng ta chỉ có thể nói về xác suất của một biến nằm trong một khoảng giá trị nhất định, ví dụ P(t₁≤X<t₂). Trong trường hợp này, phân phối xác suất được mô tả bằng hàm mật độ xác suất p(x), sao cho:

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Một dạng liên tục của phân phối đồng đều được gọi là đồng đều liên tục, được định nghĩa trên một khoảng hữu hạn. Xác suất giá trị X nằm trong một khoảng có độ dài l tỷ lệ thuận với l, và tăng lên đến 1.

Một phân phối quan trọng khác là phân phối chuẩn, mà chúng ta sẽ thảo luận chi tiết hơn bên dưới.

Giá trị Trung bình, Phương sai và Độ lệch Chuẩn

Giả sử chúng ta lấy một dãy n mẫu của một biến ngẫu nhiên X: x₁, x₂, ..., x_n. Chúng ta có thể định nghĩa giá trị trung bình (hoặc trung bình số học) của dãy theo cách truyền thống là (x₁+x₂+x_n)/n. Khi kích thước mẫu tăng lên (tức là lấy giới hạn với n→∞), chúng ta sẽ thu được giá trị trung bình (còn gọi là kỳ vọng) của phân phối. Chúng ta sẽ ký hiệu kỳ vọng là E(x).

Có thể chứng minh rằng đối với bất kỳ phân phối rời rạc nào với các giá trị {x₁, x₂, ..., x_N} và các xác suất tương ứng p₁, p₂, ..., p_N, kỳ vọng sẽ bằng E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Để xác định mức độ phân tán của các giá trị, chúng ta có thể tính phương sai σ² = ∑(x_i - μ)²/n, trong đó μ là giá trị trung bình của dãy. Giá trị σ được gọi là độ lệch chuẩn, và σ² được gọi là phương sai.

Giá trị Mode, Median và Quartiles

Đôi khi, giá trị trung bình không đại diện đầy đủ cho giá trị "điển hình" của dữ liệu. Ví dụ, khi có một vài giá trị cực đoan hoàn toàn nằm ngoài phạm vi, chúng có thể ảnh hưởng đến giá trị trung bình. Một chỉ số tốt khác là median, giá trị mà một nửa số điểm dữ liệu thấp hơn nó, và nửa còn lại cao hơn.

Để giúp chúng ta hiểu phân phối dữ liệu, rất hữu ích khi nói về quartiles:

Quartile thứ nhất, hoặc Q1, là giá trị mà 25% dữ liệu nằm dưới nó
Quartile thứ ba, hoặc Q3, là giá trị mà 75% dữ liệu nằm dưới nó

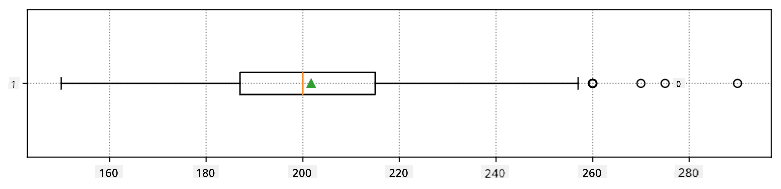
Chúng ta có thể biểu diễn mối quan hệ giữa median và quartiles bằng một biểu đồ gọi là box plot:

Ở đây chúng ta cũng tính khoảng giữa các quartile IQR=Q3-Q1, và các giá trị ngoại lệ - những giá trị nằm ngoài các giới hạn [Q1-1.5IQR,Q3+1.5IQR].

Đối với phân phối hữu hạn chứa một số lượng nhỏ các giá trị có thể, một giá trị "điển hình" tốt là giá trị xuất hiện thường xuyên nhất, được gọi là mode. Nó thường được áp dụng cho dữ liệu phân loại, chẳng hạn như màu sắc. Hãy xem xét tình huống khi chúng ta có hai nhóm người - một nhóm thích màu đỏ, và nhóm kia thích màu xanh. Nếu chúng ta mã hóa màu sắc bằng các con số, giá trị trung bình cho màu yêu thích sẽ nằm đâu đó trong phổ màu cam-xanh lá, điều này không phản ánh sở thích thực sự của cả hai nhóm. Tuy nhiên, mode sẽ là một trong hai màu, hoặc cả hai màu, nếu số người chọn chúng bằng nhau (trong trường hợp này chúng ta gọi mẫu là đa mode).

Dữ liệu Thực tế

Khi chúng ta phân tích dữ liệu từ thực tế, chúng thường không phải là biến ngẫu nhiên theo nghĩa rằng chúng ta không thực hiện các thí nghiệm với kết quả không xác định. Ví dụ, hãy xem xét một đội bóng chày và dữ liệu cơ thể của họ, chẳng hạn như chiều cao, cân nặng và tuổi. Những con số này không hoàn toàn ngẫu nhiên, nhưng chúng ta vẫn có thể áp dụng các khái niệm toán học tương tự. Ví dụ, một dãy cân nặng của mọi người có thể được coi là một dãy giá trị được lấy từ một biến ngẫu nhiên nào đó. Dưới đây là dãy cân nặng của các cầu thủ bóng chày thực tế từ Major League Baseball, được lấy từ bộ dữ liệu này (để tiện lợi, chỉ hiển thị 20 giá trị đầu tiên):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Note: Để xem ví dụ về cách làm việc với bộ dữ liệu này, hãy xem notebook đi kèm. Ngoài ra còn có một số thử thách trong bài học này, và bạn có thể hoàn thành chúng bằng cách thêm một số mã vào notebook đó. Nếu bạn không chắc cách thao tác với dữ liệu, đừng lo lắng - chúng ta sẽ quay lại làm việc với dữ liệu bằng Python sau này. Nếu bạn không biết cách chạy mã trong Jupyter Notebook, hãy xem bài viết này.

Dưới đây là biểu đồ box plot hiển thị giá trị trung bình, median và quartiles cho dữ liệu của chúng ta:

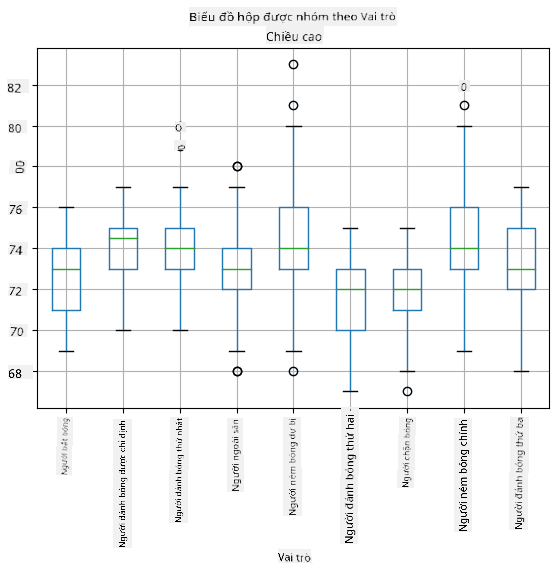
Vì dữ liệu của chúng ta chứa thông tin về các vai trò của cầu thủ, chúng ta cũng có thể tạo box plot theo vai trò - điều này sẽ cho phép chúng ta hiểu cách các giá trị tham số khác nhau giữa các vai trò. Lần này chúng ta sẽ xem xét chiều cao:

Biểu đồ này cho thấy rằng, trung bình, chiều cao của các cầu thủ ở vị trí đầu tiên cao hơn chiều cao của các cầu thủ ở vị trí thứ hai. Sau này trong bài học, chúng ta sẽ học cách kiểm tra giả thuyết này một cách chính thức hơn, và cách chứng minh rằng dữ liệu của chúng ta có ý nghĩa thống kê để thể hiện điều đó.

Khi làm việc với dữ liệu thực tế, chúng ta giả định rằng tất cả các điểm dữ liệu là các mẫu được lấy từ một phân phối xác suất nào đó. Giả định này cho phép chúng ta áp dụng các kỹ thuật học máy và xây dựng các mô hình dự đoán hoạt động.

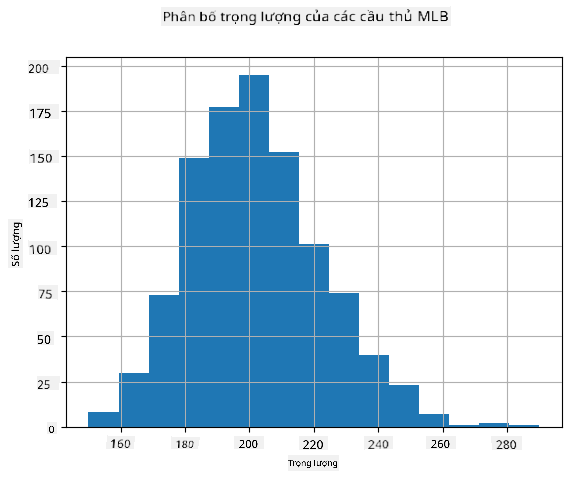
Để xem phân phối của dữ liệu của chúng ta, chúng ta có thể vẽ một biểu đồ gọi là histogram. Trục X sẽ chứa một số khoảng cân nặng khác nhau (gọi là bins), và trục Y sẽ hiển thị số lần mẫu biến ngẫu nhiên nằm trong một khoảng nhất định.

Từ biểu đồ histogram này, bạn có thể thấy rằng tất cả các giá trị tập trung xung quanh một giá trị trung bình cân nặng nhất định, và càng xa giá trị trung bình đó - càng ít giá trị cân nặng được gặp. Tức là, rất khó xảy ra rằng cân nặng của một cầu thủ bóng chày sẽ rất khác so với cân nặng trung bình. Phương sai của cân nặng cho thấy mức độ mà các cân nặng có khả năng khác biệt so với giá trị trung bình.

Nếu chúng ta lấy cân nặng của những người khác, không phải từ giải bóng chày, phân phối có thể sẽ khác. Tuy nhiên, hình dạng của phân phối sẽ giống nhau, nhưng giá trị trung bình và phương sai sẽ thay đổi. Vì vậy, nếu chúng ta huấn luyện mô hình của mình trên các cầu thủ bóng chày, nó có thể đưa ra kết quả sai khi áp dụng cho sinh viên của một trường đại học, vì phân phối cơ bản là khác nhau.

Phân phối Chuẩn

Phân phối cân nặng mà chúng ta đã thấy ở trên rất điển hình, và nhiều phép đo từ thực tế tuân theo cùng một loại phân phối, nhưng với giá trị trung bình và phương sai khác nhau. Phân phối này được gọi là phân phối chuẩn, và nó đóng vai trò rất quan trọng trong thống kê.

Sử dụng phân phối chuẩn là cách đúng để tạo ra các cân nặng ngẫu nhiên của các cầu thủ bóng chày tiềm năng. Một khi chúng ta biết cân nặng trung bình mean và độ lệch chuẩn std, chúng ta có thể tạo ra 1000 mẫu cân nặng theo cách sau:

samples = np.random.normal(mean,std,1000)

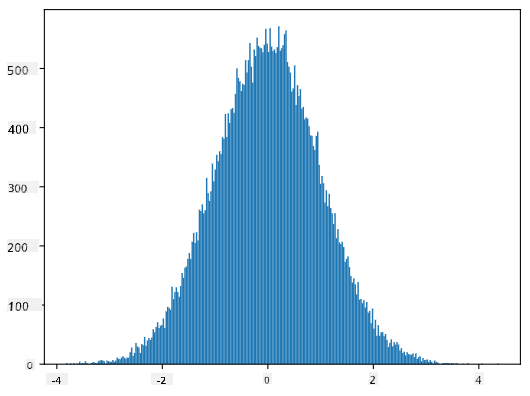
Nếu chúng ta vẽ biểu đồ histogram của các mẫu được tạo ra, chúng ta sẽ thấy hình ảnh rất giống với hình ảnh được hiển thị ở trên. Và nếu chúng ta tăng số lượng mẫu và số lượng bins, chúng ta có thể tạo ra hình ảnh của một phân phối chuẩn gần với lý tưởng hơn:

Phân phối Chuẩn với mean=0 và std.dev=1

Khoảng Tin cậy

Khi chúng ta nói về cân nặng của các cầu thủ bóng chày, chúng ta giả định rằng có một biến ngẫu nhiên W tương ứng với phân phối xác suất lý tưởng của cân nặng của tất cả các cầu thủ bóng chày (gọi là quần thể). Dãy cân nặng của chúng ta tương ứng với một tập hợp con của tất cả các cầu thủ bóng chày mà chúng ta gọi là mẫu. Một câu hỏi thú vị là, liệu chúng ta có thể biết các tham số của phân phối W, tức là giá trị trung bình và phương sai của quần thể?

Câu trả lời dễ nhất là tính giá trị trung bình và phương sai của mẫu của chúng ta. Tuy nhiên, có thể xảy ra trường hợp mẫu ngẫu nhiên của chúng ta không đại diện chính xác cho toàn bộ quần thể. Vì vậy, có ý nghĩa khi nói về khoảng tin cậy.

Khoảng tin cậy là sự ước tính giá trị trung bình thực của tổng thể dựa trên mẫu của chúng ta, với độ chính xác trong một xác suất nhất định (hoặc mức độ tin cậy). Giả sử chúng ta có một mẫu X₁, ..., X_n từ phân phối của mình. Mỗi lần chúng ta lấy mẫu từ phân phối, chúng ta sẽ thu được một giá trị trung bình μ khác nhau. Do đó, μ có thể được coi là một biến ngẫu nhiên. Một khoảng tin cậy với độ tin cậy p là một cặp giá trị (L_p,R_p), sao cho P(L_p≤μ≤R_p) = p, tức là xác suất giá trị trung bình đo được nằm trong khoảng này bằng p.

Việc giải thích chi tiết cách tính các khoảng tin cậy vượt quá phạm vi giới thiệu ngắn gọn này. Một số chi tiết thêm có thể được tìm thấy trên Wikipedia. Tóm lại, chúng ta định nghĩa phân phối của giá trị trung bình mẫu được tính toán so với giá trị trung bình thực của tổng thể, được gọi là phân phối Student.

Sự thật thú vị: Phân phối Student được đặt tên theo nhà toán học William Sealy Gosset, người đã xuất bản bài báo của mình dưới bút danh "Student". Ông làm việc tại nhà máy bia Guinness, và theo một số nguồn tin, chủ của ông không muốn công chúng biết rằng họ đang sử dụng các kiểm định thống kê để xác định chất lượng nguyên liệu thô.

Nếu chúng ta muốn ước lượng giá trị trung bình μ của tổng thể với độ tin cậy p, chúng ta cần lấy phân vị (1-p)/2 của phân phối Student A, giá trị này có thể được lấy từ bảng hoặc tính toán bằng các hàm tích hợp trong phần mềm thống kê (ví dụ: Python, R, v.v.). Sau đó, khoảng cho μ sẽ được tính bằng X±A*D/√n, trong đó X là giá trị trung bình của mẫu, D là độ lệch chuẩn.

Lưu ý: Chúng ta cũng bỏ qua việc thảo luận về một khái niệm quan trọng là bậc tự do, điều này rất quan trọng liên quan đến phân phối Student. Bạn có thể tham khảo các sách thống kê đầy đủ hơn để hiểu sâu hơn về khái niệm này.

Một ví dụ về tính khoảng tin cậy cho cân nặng và chiều cao được đưa ra trong notebook đi kèm.

p	Giá trị trung bình cân nặng
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Lưu ý rằng độ tin cậy càng cao thì khoảng tin cậy càng rộng.

Kiểm định giả thuyết

Trong tập dữ liệu các cầu thủ bóng chày, có các vai trò khác nhau của cầu thủ, được tóm tắt dưới đây (xem notebook đi kèm để biết cách tính bảng này):

Vai trò	Chiều cao	Cân nặng	Số lượng
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

Chúng ta có thể nhận thấy rằng chiều cao trung bình của các cầu thủ First Basemen cao hơn so với Second Basemen. Do đó, chúng ta có thể bị cám dỗ để kết luận rằng các cầu thủ First Basemen cao hơn các cầu thủ Second Basemen.

Phát biểu này được gọi là giả thuyết, vì chúng ta không biết liệu điều này có thực sự đúng hay không.

Tuy nhiên, không phải lúc nào cũng rõ ràng liệu chúng ta có thể đưa ra kết luận này hay không. Từ thảo luận ở trên, chúng ta biết rằng mỗi giá trị trung bình có một khoảng tin cậy liên quan, và do đó sự khác biệt này có thể chỉ là một sai số thống kê. Chúng ta cần một cách chính thức hơn để kiểm tra giả thuyết của mình.

Hãy tính các khoảng tin cậy riêng biệt cho chiều cao của các cầu thủ First Basemen và Second Basemen:

Độ tin cậy	First Basemen	Second Basemen
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Chúng ta có thể thấy rằng không có khoảng tin cậy nào bị chồng lấn. Điều này chứng minh giả thuyết rằng các cầu thủ First Basemen cao hơn các cầu thủ Second Basemen.

Một cách chính thức hơn, vấn đề chúng ta đang giải quyết là xem liệu hai phân phối xác suất có giống nhau hay không, hoặc ít nhất có cùng tham số. Tùy thuộc vào phân phối, chúng ta cần sử dụng các kiểm định khác nhau. Nếu chúng ta biết rằng các phân phối của mình là chuẩn, chúng ta có thể áp dụng kiểm định Student t-test.

Trong kiểm định Student t-test, chúng ta tính toán một giá trị gọi là t-value, chỉ ra sự khác biệt giữa các giá trị trung bình, có tính đến phương sai. Người ta chứng minh rằng t-value tuân theo phân phối Student, điều này cho phép chúng ta lấy giá trị ngưỡng cho một mức độ tin cậy p nhất định (giá trị này có thể được tính toán hoặc tra cứu trong các bảng số). Sau đó, chúng ta so sánh t-value với giá trị ngưỡng này để chấp nhận hoặc bác bỏ giả thuyết.

Trong Python, chúng ta có thể sử dụng gói SciPy, bao gồm hàm ttest_ind (cùng với nhiều hàm thống kê hữu ích khác!). Hàm này tính toán t-value cho chúng ta, và cũng thực hiện tra cứu ngược giá trị p-value, để chúng ta chỉ cần nhìn vào độ tin cậy để đưa ra kết luận.

Ví dụ, so sánh giữa chiều cao của các cầu thủ First Basemen và Second Basemen cho chúng ta kết quả sau:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

Trong trường hợp của chúng ta, giá trị p-value rất thấp, điều này có nghĩa là có bằng chứng mạnh mẽ ủng hộ rằng các cầu thủ First Basemen cao hơn.

Cũng có nhiều loại giả thuyết khác mà chúng ta có thể muốn kiểm tra, ví dụ:

Chứng minh rằng một mẫu nhất định tuân theo một phân phối nào đó. Trong trường hợp của chúng ta, chúng ta đã giả định rằng chiều cao được phân phối chuẩn, nhưng điều này cần được xác minh thống kê chính thức.
Chứng minh rằng giá trị trung bình của một mẫu tương ứng với một giá trị được xác định trước.
So sánh giá trị trung bình của một số mẫu (ví dụ: sự khác biệt về mức độ hạnh phúc giữa các nhóm tuổi khác nhau).

Định luật số lớn và Định lý giới hạn trung tâm

Một trong những lý do tại sao phân phối chuẩn lại quan trọng là định lý giới hạn trung tâm. Giả sử chúng ta có một mẫu lớn gồm N giá trị độc lập X₁, ..., X_N, được lấy mẫu từ bất kỳ phân phối nào với giá trị trung bình μ và phương sai σ². Sau đó, khi N đủ lớn (nói cách khác, khi N→∞), giá trị trung bình Σ_iX_i sẽ được phân phối chuẩn, với giá trị trung bình μ và phương sai σ²/N.

Một cách khác để diễn giải định lý giới hạn trung tâm là nói rằng bất kể phân phối ban đầu, khi bạn tính giá trị trung bình của tổng các giá trị biến ngẫu nhiên, bạn sẽ thu được phân phối chuẩn.

Từ định lý giới hạn trung tâm, cũng có thể suy ra rằng, khi N→∞, xác suất giá trị trung bình mẫu bằng μ sẽ tiến tới 1. Điều này được gọi là định luật số lớn.

Hiệp phương sai và Tương quan

Một trong những điều mà Khoa học Dữ liệu làm là tìm kiếm mối quan hệ giữa các dữ liệu. Chúng ta nói rằng hai dãy số tương quan khi chúng thể hiện hành vi tương tự tại cùng một thời điểm, tức là chúng cùng tăng/giảm đồng thời, hoặc một dãy tăng khi dãy kia giảm và ngược lại. Nói cách khác, dường như có một mối quan hệ nào đó giữa hai dãy số.

Tương quan không nhất thiết chỉ ra mối quan hệ nhân quả giữa hai dãy số; đôi khi cả hai biến có thể phụ thuộc vào một nguyên nhân bên ngoài, hoặc có thể chỉ là ngẫu nhiên mà hai dãy số tương quan. Tuy nhiên, tương quan toán học mạnh là một chỉ báo tốt rằng hai biến có liên quan đến nhau theo một cách nào đó.

Về mặt toán học, khái niệm chính thể hiện mối quan hệ giữa hai biến ngẫu nhiên là hiệp phương sai, được tính như sau: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Chúng ta tính độ lệch của cả hai biến so với giá trị trung bình của chúng, và sau đó nhân các độ lệch đó. Nếu cả hai biến lệch cùng chiều, tích sẽ luôn là giá trị dương, dẫn đến hiệp phương sai dương. Nếu cả hai biến lệch ngược chiều (tức là một biến giảm xuống dưới trung bình khi biến kia tăng lên trên trung bình), chúng ta sẽ luôn nhận được các giá trị âm, dẫn đến hiệp phương sai âm. Nếu các độ lệch không phụ thuộc, chúng sẽ cộng lại xấp xỉ bằng không.

Giá trị tuyệt đối của hiệp phương sai không cho chúng ta biết nhiều về mức độ tương quan, vì nó phụ thuộc vào độ lớn của các giá trị thực tế. Để chuẩn hóa, chúng ta có thể chia hiệp phương sai cho độ lệch chuẩn của cả hai biến, để thu được tương quan. Điều tốt là tương quan luôn nằm trong khoảng [-1,1], trong đó 1 chỉ ra tương quan dương mạnh giữa các giá trị, -1 chỉ ra tương quan âm mạnh, và 0 chỉ ra không có tương quan (các biến độc lập).

Ví dụ: Chúng ta có thể tính tương quan giữa cân nặng và chiều cao của các cầu thủ bóng chày từ tập dữ liệu đã đề cập ở trên:

print(np.corrcoef(weights,heights))

Kết quả, chúng ta thu được ma trận tương quan như sau:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Ma trận tương quan C có thể được tính cho bất kỳ số lượng dãy đầu vào S₁, ..., S_n. Giá trị của C_ij là tương quan giữa S_i và S_j, và các phần tử trên đường chéo luôn là 1 (đây cũng là tự tương quan của S_i).

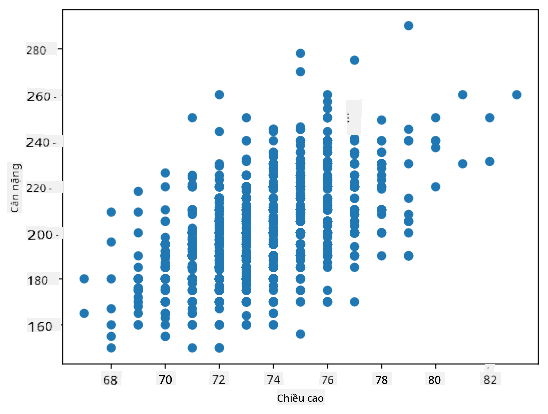
Trong trường hợp của chúng ta, giá trị 0.53 chỉ ra rằng có một số tương quan giữa cân nặng và chiều cao của một người. Chúng ta cũng có thể vẽ biểu đồ phân tán của một giá trị so với giá trị kia để thấy mối quan hệ một cách trực quan:

Nhiều ví dụ hơn về tương quan và hiệp phương sai có thể được tìm thấy trong notebook đi kèm.

Kết luận

Trong phần này, chúng ta đã học:

các thuộc tính thống kê cơ bản của dữ liệu, như giá trị trung bình, phương sai, mode và các tứ phân vị
các phân phối khác nhau của biến ngẫu nhiên, bao gồm phân phối chuẩn
cách tìm tương quan giữa các thuộc tính khác nhau
cách sử dụng các công cụ toán học và thống kê để chứng minh một số giả thuyết
cách tính khoảng tin cậy cho biến ngẫu nhiên dựa trên mẫu dữ liệu

Mặc dù đây chắc chắn không phải là danh sách đầy đủ các chủ đề trong xác suất và thống kê, nhưng nó đủ để cung cấp cho bạn một khởi đầu tốt trong khóa học này.

🚀 Thử thách

Sử dụng mã mẫu trong notebook để kiểm tra các giả thuyết khác:

Các cầu thủ First Basemen lớn tuổi hơn các cầu thủ Second Basemen
Các cầu thủ First Basemen cao hơn các cầu thủ Third Basemen
Các cầu thủ Shortstops cao hơn các cầu thủ Second Basemen

Câu hỏi sau bài giảng

Ôn tập & Tự học

Xác suất và thống kê là một chủ đề rất rộng lớn, xứng đáng có một khóa học riêng. Nếu bạn muốn đi sâu hơn vào lý thuyết, bạn có thể tiếp tục đọc một số sách sau:

Carlos Fernandez-Granda từ Đại học New York có các ghi chú bài giảng tuyệt vời Probability and Statistics for Data Science (có sẵn trực tuyến)
Peter và Andrew Bruce. Practical Statistics for Data Scientists. [mã mẫu trong R].
James D. Miller. Statistics for Data Science [mã mẫu trong R].

Bài tập

Nghiên cứu nhỏ về bệnh tiểu đường

Ghi công

Bài học này được viết với ♥️ bởi Dmitry Soshnikov

Tuyên bố miễn trừ trách nhiệm:
Tài liệu này đã được dịch bằng dịch vụ dịch thuật AI Co-op Translator. Mặc dù chúng tôi cố gắng đảm bảo độ chính xác, xin lưu ý rằng các bản dịch tự động có thể chứa lỗi hoặc không chính xác. Tài liệu gốc bằng ngôn ngữ bản địa nên được coi là nguồn thông tin chính thức. Đối với các thông tin quan trọng, khuyến nghị sử dụng dịch vụ dịch thuật chuyên nghiệp bởi con người. Chúng tôi không chịu trách nhiệm cho bất kỳ sự hiểu lầm hoặc diễn giải sai nào phát sinh từ việc sử dụng bản dịch này.

30 KiB Raw Permalink Blame History Unescape Escape