35 KiB

Raw Permalink Blame History Unescape Escape

شماریات اور احتمال کا مختصر تعارف


شماریات اور احتمال - اسکیچ نوٹ @nitya کی طرف سے

شماریات اور احتمال کا نظریہ ریاضی کے دو ایسے شعبے ہیں جو ڈیٹا سائنس کے لیے بہت اہم ہیں۔ ڈیٹا کے ساتھ کام کرنا ممکن ہے بغیر ریاضی کی گہری معلومات کے، لیکن کچھ بنیادی تصورات جاننا بہتر ہے۔ یہاں ہم ایک مختصر تعارف پیش کریں گے جو آپ کو شروع کرنے میں مدد دے گا۔

لیکچر سے پہلے کا کوئز

احتمال اور بے ترتیب متغیرات

احتمال 0 اور 1 کے درمیان ایک عدد ہے جو کسی واقعہ کے ہونے کے امکان کو ظاہر کرتا ہے۔ یہ مثبت نتائج کی تعداد (جو واقعہ کی طرف لے جاتے ہیں) کو کل نتائج کی تعداد سے تقسیم کر کے بیان کیا جاتا ہے، بشرطیکہ تمام نتائج برابر احتمال رکھتے ہوں۔ مثال کے طور پر، جب ہم ایک ڈائس پھینکتے ہیں، تو ایک جفت عدد حاصل کرنے کا احتمال 3/6 = 0.5 ہے۔

جب ہم واقعات کی بات کرتے ہیں، تو ہم بے ترتیب متغیرات استعمال کرتے ہیں۔ مثال کے طور پر، وہ بے ترتیب متغیر جو ڈائس پھینکنے پر حاصل ہونے والے عدد کو ظاہر کرتا ہے، وہ 1 سے 6 تک کے عدد لے سکتا ہے۔ 1 سے 6 تک کے عددوں کا مجموعہ نمونہ جگہ کہلاتا ہے۔ ہم بے ترتیب متغیر کے کسی خاص عدد لینے کے احتمال کے بارے میں بات کر سکتے ہیں، جیسے P(X=3)=1/6۔

پچھلی مثال میں بے ترتیب متغیر کو منقطع کہا جاتا ہے، کیونکہ اس کی نمونہ جگہ گنی جا سکتی ہے، یعنی الگ الگ عدد ہیں جنہیں شمار کیا جا سکتا ہے۔ کچھ صورتوں میں نمونہ جگہ حقیقی عددوں کی حد ہوتی ہے، یا حقیقی عددوں کا پورا مجموعہ۔ ایسے متغیرات کو مسلسل کہا جاتا ہے۔ ایک اچھی مثال بس کے پہنچنے کا وقت ہے۔

احتمال کی تقسیم

منقطع بے ترتیب متغیرات کے معاملے میں، ہر واقعہ کے احتمال کو ایک فنکشن P(X) کے ذریعے بیان کرنا آسان ہے۔ نمونہ جگہ S کے ہر عدد s کے لیے یہ 0 سے 1 تک کا عدد دے گا، اس طرح کہ تمام واقعات کے لیے P(X=s) کے تمام عددوں کا مجموعہ 1 ہوگا۔

سب سے مشہور منقطع تقسیم یکساں تقسیم ہے، جس میں نمونہ جگہ کے N عناصر ہوتے ہیں، اور ہر ایک کے لیے برابر احتمال 1/N ہوتا ہے۔

مسلسل متغیر کی احتمال تقسیم کو بیان کرنا زیادہ مشکل ہے، جس کے عدد کسی وقفہ [a,b] یا حقیقی عددوں کے پورے مجموعہ ℝ سے لیے جاتے ہیں۔ بس کے پہنچنے کے وقت کے معاملے پر غور کریں۔ حقیقت میں، کسی خاص وقت t پر بس کے بالکل اسی وقت پہنچنے کا احتمال 0 ہے!

اب آپ جانتے ہیں کہ 0 احتمال والے واقعات ہوتے ہیں، اور اکثر ہوتے ہیں! کم از کم ہر بار جب بس پہنچتی ہے!

ہم صرف کسی متغیر کے کسی دیے گئے وقفہ میں عدد لینے کے احتمال کے بارے میں بات کر سکتے ہیں، جیسے P(t₁≤X<t₂)۔ اس صورت میں، احتمال تقسیم کو احتمال کثافت فنکشن p(x) کے ذریعے بیان کیا جاتا ہے، اس طرح کہ

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

یکساں تقسیم کا مسلسل متبادل مسلسل یکساں تقسیم کہلاتا ہے، جو ایک محدود وقفہ پر بیان کیا جاتا ہے۔ احتمال کہ عدد X کسی وقفہ کی لمبائی l میں آتا ہے، l کے تناسب سے ہوتا ہے، اور 1 تک بڑھتا ہے۔

ایک اور اہم تقسیم معمولی تقسیم ہے، جس کے بارے میں ہم نیچے مزید تفصیل سے بات کریں گے۔

اوسط، تغیر اور معیاری انحراف

فرض کریں ہم بے ترتیب متغیر X کے n نمونوں کی ترتیب نکالتے ہیں: x₁, x₂, ..., x_n۔ ہم ترتیب کی اوسط (یا حسابی اوسط) کو روایتی طریقے سے (x₁+x₂+x_n)/n کے طور پر بیان کر سکتے ہیں۔ جیسے جیسے ہم نمونہ کا سائز بڑھاتے ہیں (یعنی n→∞ کی حد لیتے ہیں)، ہم تقسیم کی اوسط (جسے توقع بھی کہا جاتا ہے) حاصل کریں گے۔ ہم توقع کو E(x) سے ظاہر کریں گے۔

یہ دکھایا جا سکتا ہے کہ کسی بھی منقطع تقسیم کے لیے جس کے عدد {x₁, x₂, ..., x_N} اور متعلقہ احتمالات p₁, p₂, ..., p_N ہوں، توقع E(X)=x₁p₁+x₂p₂+...+x_Np_N کے برابر ہوگی۔

یہ معلوم کرنے کے لیے کہ عدد کتنے دور تک پھیلے ہوئے ہیں، ہم تغیر σ² = ∑(x_i - μ)²/n کا حساب لگا سکتے ہیں، جہاں μ ترتیب کی اوسط ہے۔ عدد σ کو معیاری انحراف کہا جاتا ہے، اور σ² کو تغیر کہا جاتا ہے۔

موڈ، میڈین اور کوارٹائلز

کبھی کبھی، اوسط ڈیٹا کے "عام" عدد کو مناسب طریقے سے ظاہر نہیں کرتی۔ مثال کے طور پر، جب کچھ انتہائی عدد ہوتے ہیں جو مکمل طور پر حد سے باہر ہوتے ہیں، وہ اوسط کو متاثر کر سکتے ہیں۔ ایک اور اچھا اشارہ میڈین ہے، ایک عدد ایسا کہ آدھے ڈیٹا پوائنٹس اس سے کم ہوں، اور باقی آدھے - زیادہ۔

ڈیٹا کی تقسیم کو سمجھنے میں مدد کے لیے، کوارٹائلز کے بارے میں بات کرنا مفید ہے:

پہلا کوارٹائل، یا Q1، ایک عدد ہے، جس کے نیچے 25% ڈیٹا آتا ہے
تیسرا کوارٹائل، یا Q3، ایک عدد ہے جس کے نیچے 75% ڈیٹا آتا ہے

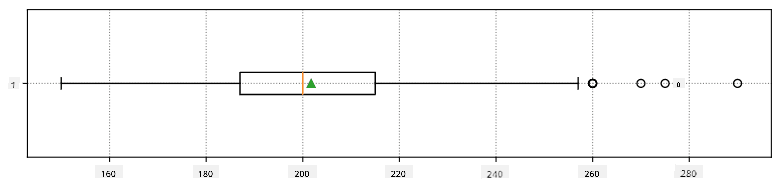
گرافک طور پر ہم میڈین اور کوارٹائلز کے تعلق کو ایک ڈایاگرام میں ظاہر کر سکتے ہیں جسے باکس پلاٹ کہا جاتا ہے:

یہاں ہم انٹر-کوارٹائل رینج IQR=Q3-Q1 کا حساب لگاتے ہیں، اور نام نہاد آؤٹ لائرز - عدد جو حدود [Q1-1.5IQR,Q3+1.5IQR] سے باہر ہوتے ہیں۔

محدود تقسیم جو ممکنہ عدد کی ایک چھوٹی تعداد پر مشتمل ہو، ایک اچھا "عام" عدد وہ ہوتا ہے جو سب سے زیادہ بار ظاہر ہوتا ہے، جسے موڈ کہا جاتا ہے۔ یہ اکثر زمرہ جاتی ڈیٹا پر لاگو ہوتا ہے، جیسے رنگ۔ تصور کریں کہ ہمارے پاس لوگوں کے دو گروپ ہیں - کچھ جو سرخ کو بہت پسند کرتے ہیں، اور دوسرے جو نیلے کو پسند کرتے ہیں۔ اگر ہم رنگوں کو عددوں سے کوڈ کریں، تو پسندیدہ رنگ کے لیے اوسط عدد کہیں نارنجی-سبز اسپیکٹرم میں ہوگا، جو کسی بھی گروپ کی اصل پسند کو ظاہر نہیں کرتا۔ تاہم، موڈ یا تو ایک رنگ ہوگا، یا دونوں رنگ، اگر ان کے لیے ووٹ دینے والے لوگوں کی تعداد برابر ہو (اس صورت میں ہم نمونہ کو ملٹی موڈل کہتے ہیں)۔

حقیقی دنیا کا ڈیٹا

جب ہم حقیقی زندگی کے ڈیٹا کا تجزیہ کرتے ہیں، تو وہ اکثر بے ترتیب متغیرات کی طرح نہیں ہوتے، اس معنی میں کہ ہم نامعلوم نتیجے کے ساتھ تجربات نہیں کرتے۔ مثال کے طور پر، بیس بال کھلاڑیوں کی ایک ٹیم پر غور کریں، اور ان کے جسمانی ڈیٹا، جیسے قد، وزن اور عمر۔ یہ عدد بالکل بے ترتیب نہیں ہیں، لیکن ہم پھر بھی وہی ریاضیاتی تصورات لاگو کر سکتے ہیں۔ مثال کے طور پر، لوگوں کے وزن کی ترتیب کو کسی بے ترتیب متغیر سے لیے گئے عددوں کی ترتیب سمجھا جا سکتا ہے۔ نیچے میجر لیگ بیس بال کے حقیقی بیس بال کھلاڑیوں کے وزن کی ترتیب دی گئی ہے، جو اس ڈیٹا سیٹ سے لی گئی ہے (آپ کی سہولت کے لیے، صرف پہلے 20 عدد دکھائے گئے ہیں):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

نوٹ: اس ڈیٹا سیٹ کے ساتھ کام کرنے کی مثال دیکھنے کے لیے، ساتھ والے نوٹ بک پر نظر ڈالیں۔ اس سبق میں کئی چیلنجز بھی ہیں، اور آپ انہیں اس نوٹ بک میں کچھ کوڈ شامل کر کے مکمل کر سکتے ہیں۔ اگر آپ کو ڈیٹا پر کام کرنے کا طریقہ معلوم نہیں ہے، تو فکر نہ کریں - ہم بعد میں پائتھن کا استعمال کرتے ہوئے ڈیٹا پر کام کرنے پر واپس آئیں گے۔ اگر آپ کو جیوپیٹر نوٹ بک میں کوڈ چلانے کا طریقہ معلوم نہیں ہے، تو اس مضمون پر نظر ڈالیں۔

یہاں ہمارے ڈیٹا کے لیے اوسط، میڈین اور کوارٹائلز کو ظاہر کرنے والا باکس پلاٹ ہے:

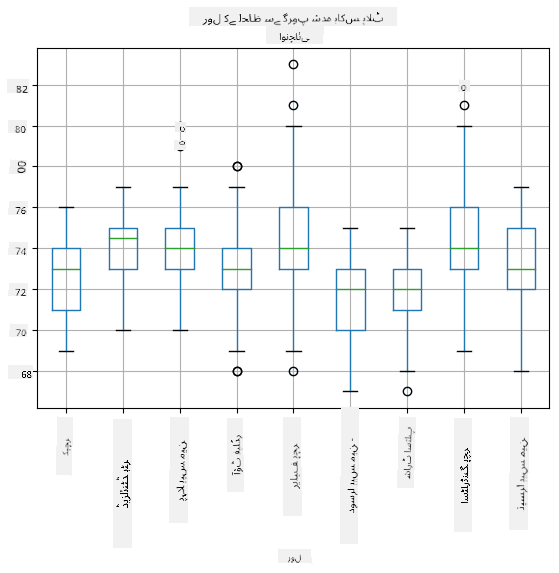
چونکہ ہمارے ڈیٹا میں مختلف کھلاڑیوں کے کردار کے بارے میں معلومات شامل ہیں، ہم کردار کے لحاظ سے بھی باکس پلاٹ بنا سکتے ہیں - یہ ہمیں یہ سمجھنے کی اجازت دے گا کہ پیرامیٹرز کے عدد کرداروں کے لحاظ سے کیسے مختلف ہیں۔ اس بار ہم قد پر غور کریں گے:

یہ ڈایاگرام تجویز کرتا ہے کہ، اوسطاً، پہلے بیس مین کا قد دوسرے بیس مین کے قد سے زیادہ ہے۔ اس سبق میں بعد میں ہم سیکھیں گے کہ ہم اس مفروضے کو زیادہ رسمی طور پر کیسے جانچ سکتے ہیں، اور یہ کیسے ظاہر کر سکتے ہیں کہ ہمارا ڈیٹا شماریاتی طور پر اہم ہے۔

جب ہم حقیقی دنیا کے ڈیٹا پر کام کرتے ہیں، تو ہم فرض کرتے ہیں کہ تمام ڈیٹا پوائنٹس کسی احتمال تقسیم سے لیے گئے نمونے ہیں۔ یہ مفروضہ ہمیں مشین لرننگ تکنیکوں کو لاگو کرنے اور کام کرنے والے پیش گوئی ماڈلز بنانے کی اجازت دیتا ہے۔

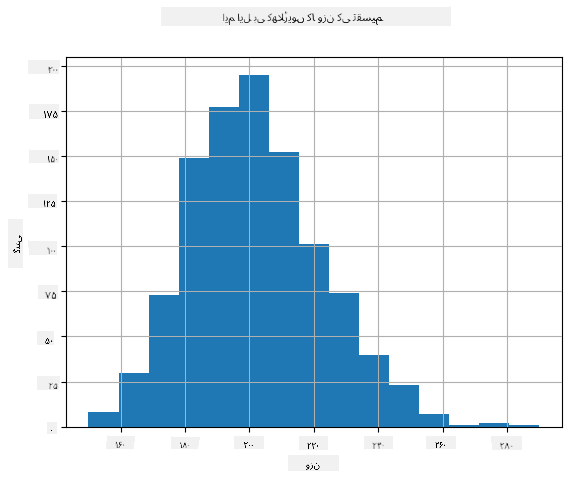
اپنے ڈیٹا کی تقسیم کو دیکھنے کے لیے، ہم ایک گراف بنا سکتے ہیں جسے ہسٹوگرام کہا جاتا ہے۔ X-محور مختلف وزن کے وقفوں (نام نہاد بِنز) کی تعداد پر مشتمل ہوگا، اور عمودی محور یہ ظاہر کرے گا کہ ہمارا بے ترتیب متغیر نمونہ دیے گئے وقفے میں کتنی بار آیا۔

اس ہسٹوگرام سے آپ دیکھ سکتے ہیں کہ تمام عدد ایک خاص اوسط وزن کے ارد گرد مرکوز ہیں، اور جیسے جیسے ہم اس وزن سے دور جاتے ہیں - اس وزن کے عدد کم ملتے ہیں۔ یعنی، یہ بہت غیر ممکن ہے کہ کسی بیس بال کھلاڑی کا وزن اوسط وزن سے بہت مختلف ہو۔ وزن کا تغیر یہ ظاہر کرتا ہے کہ وزن اوسط سے کتنے مختلف ہونے کا امکان ہے۔

اگر ہم دوسرے لوگوں کے وزن لیں، جو بیس بال لیگ سے نہیں ہیں، تو تقسیم مختلف ہونے کا امکان ہے۔ تاہم، تقسیم کی شکل وہی ہوگی، لیکن اوسط اور تغیر بدل جائیں گے۔ لہذا، اگر ہم اپنے ماڈل کو بیس بال کھلاڑیوں پر تربیت دیں، تو یہ ممکن ہے کہ جب اسے کسی یونیورسٹی کے طلباء پر لاگو کیا جائے تو غلط نتائج دے، کیونکہ بنیادی تقسیم مختلف ہے۔

معمولی تقسیم

وزن کی تقسیم جو ہم نے اوپر دیکھی، بہت عام ہے، اور حقیقی دنیا سے بہت سی پیمائشیں اسی قسم کی تقسیم کی پیروی کرتی ہیں، لیکن مختلف اوسط اور تغیر کے ساتھ۔ اس تقسیم کو معمولی تقسیم کہا جاتا ہے، اور یہ شماریات میں بہت اہم کردار ادا کرتی ہے۔

معمولی تقسیم کا استعمال ممکنہ بیس بال کھلاڑیوں کے بے ترتیب وزن پیدا کرنے کا صحیح طریقہ ہے۔ ایک بار جب ہم اوسط وزن mean اور معیاری انحراف std جان لیں، تو ہم 1000 وزن کے نمونے درج ذیل طریقے سے پیدا کر سکتے ہیں:

samples = np.random.normal(mean,std,1000)

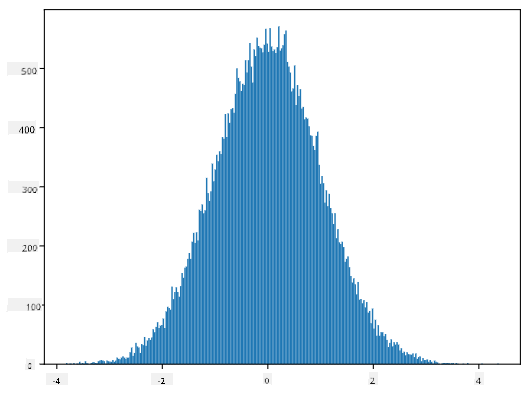
اگر ہم پیدا کردہ نمونوں کا ہسٹوگرام بنائیں، تو ہمیں اوپر دکھائی گئی تصویر سے بہت ملتی جلتی تصویر نظر آئے گی۔ اور اگر ہم نمونوں کی تعداد اور بِنز کی تعداد بڑھائیں، تو ہم معمولی تقسیم کی ایک تصویر پیدا کر سکتے ہیں جو مثالی کے قریب ہو:

معمولی تقسیم اوسط=0 اور معیاری انحراف=1 کے ساتھ

اعتماد کے وقفے

جب ہم بیس بال کھلاڑیوں کے وزن کی بات کرتے ہیں، تو ہم فرض کرتے ہیں کہ ایک بے ترتیب متغیر W ہے جو تمام بیس بال کھلاڑیوں کے وزن کی مثالی احتمال تقسیم سے مطابقت رکھتا ہے (نام نہاد آبادی). ہمارا وزن کا نمونہ تمام بیس بال کھلاڑیوں کے ایک ذیلی مجموعہ سے مطابقت رکھتا ہے جسے ہم نمونہ کہتے ہیں۔ ایک دلچسپ سوال یہ ہے کہ کیا ہم W کی تقسیم کے پیرامیٹرز، یعنی آبادی کی اوسط اور تغیر، جان سکتے ہیں؟

سب سے آسان جواب یہ ہوگا کہ ہمارے نمونہ کی اوسط اور تغیر کا حساب لگائیں۔ تاہم، یہ ممکن ہے کہ ہمارا بے ترتیب نمونہ مکمل آبادی کی درست نمائندگی نہ کرے۔ لہذا اعتماد کے وقفے کے بارے میں بات کرنا معنی رکھتا ہے۔

اعتمادی وقفہ ہماری نمونے کی بنیاد پر آبادی کے حقیقی اوسط کا اندازہ ہے، جو ایک خاص امکان (یا اعتماد کی سطح) کے ساتھ درست ہوتا ہے۔ فرض کریں کہ ہمارے پاس X₁, ..., X_n کا نمونہ ہے جو ہماری تقسیم سے لیا گیا ہے۔ ہر بار جب ہم اپنی تقسیم سے نمونہ لیتے ہیں، تو ہمیں مختلف اوسط قدر μ ملے گی۔ اس طرح μ کو ایک تصادفی متغیر سمجھا جا سکتا ہے۔ اعتماد وقفہ جس کا اعتماد p ہو، دو قدروں (L_p,R_p) کا جوڑا ہوتا ہے، اس طرح کہ P(L_p≤μ≤R_p) = p، یعنی ماپے گئے اوسط قدر کے وقفے میں آنے کا امکان p کے برابر ہوتا ہے۔

یہ مختصر تعارف سے آگے بڑھ کر تفصیل سے بحث کرنا ممکن نہیں کہ یہ اعتماد وقفے کیسے حساب کیے جاتے ہیں۔ مزید تفصیلات ویکیپیڈیا پر مل سکتی ہیں۔ مختصراً، ہم نمونے کی اوسط کی تقسیم کو آبادی کی حقیقی اوسط کے لحاظ سے بیان کرتے ہیں، جسے طالب علم کی تقسیم کہا جاتا ہے۔

دلچسپ حقیقت: طالب علم کی تقسیم کا نام ریاضی دان ولیم سیلی گوسٹ کے نام پر رکھا گیا ہے، جنہوں نے اپنا مقالہ "طالب علم" کے قلمی نام سے شائع کیا۔ وہ گینیس بریوری میں کام کرتے تھے، اور ایک روایت کے مطابق، ان کے آجر نہیں چاہتے تھے کہ عام عوام کو معلوم ہو کہ وہ خام مال کے معیار کا تعین کرنے کے لیے شماریاتی ٹیسٹ استعمال کر رہے ہیں۔

اگر ہم اپنی آبادی کی اوسط μ کو اعتماد p کے ساتھ اندازہ لگانا چاہتے ہیں، تو ہمیں طالب علم کی تقسیم A کا (1-p)/2 واں پرسنٹائل لینا ہوگا، جو یا تو جدولوں سے لیا جا سکتا ہے، یا شماریاتی سافٹ ویئر (جیسے Python، R، وغیرہ) کے کچھ بلٹ ان فنکشنز کا استعمال کرتے ہوئے حساب کیا جا سکتا ہے۔ پھر μ کے لیے وقفہ X±A*D/√n ہوگا، جہاں X نمونے کی حاصل شدہ اوسط ہے، اور D معیاری انحراف ہے۔

نوٹ: ہم آزادی کے درجات کے ایک اہم تصور پر بحث کو بھی چھوڑ دیتے ہیں، جو طالب علم کی تقسیم کے حوالے سے اہم ہے۔ اس تصور کو گہرائی سے سمجھنے کے لیے آپ شماریات پر مکمل کتابوں کا حوالہ دے سکتے ہیں۔

وزن اور قد کے لیے اعتماد وقفہ کا حساب لگانے کی ایک مثال ساتھ والے نوٹ بکس میں دی گئی ہے۔

p	وزن کی اوسط
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

نوٹ کریں کہ جتنا زیادہ اعتماد کا امکان ہوگا، اتنا ہی وسیع اعتماد وقفہ ہوگا۔

مفروضہ ٹیسٹنگ

ہمارے بیس بال کھلاڑیوں کے ڈیٹا سیٹ میں مختلف کھلاڑیوں کے کردار ہیں، جنہیں نیچے خلاصہ کیا جا سکتا ہے (دیکھیں ساتھ والا نوٹ بک کہ یہ جدول کیسے حساب کیا جا سکتا ہے):

کردار	قد	وزن	تعداد
کیچر	72.723684	204.328947	76
نامزد ہٹر	74.222222	220.888889	18
فرسٹ بیس مین	74.000000	213.109091	55
آؤٹ فیلڈر	73.010309	199.113402	194
ریلیف پچر	74.374603	203.517460	315
سیکنڈ بیس مین	71.362069	184.344828	58
شارٹ اسٹاپ	71.903846	182.923077	52
اسٹارٹنگ پچر	74.719457	205.163636	221
تھرڈ بیس مین	73.044444	200.955556	45

ہم دیکھ سکتے ہیں کہ فرسٹ بیس مین کی اوسط قد سیکنڈ بیس مین سے زیادہ ہے۔ اس طرح، ہم یہ نتیجہ اخذ کرنے کی طرف مائل ہو سکتے ہیں کہ فرسٹ بیس مین سیکنڈ بیس مین سے زیادہ قد والے ہیں۔

اس بیان کو مفروضہ کہا جاتا ہے، کیونکہ ہمیں معلوم نہیں کہ یہ حقیقت میں درست ہے یا نہیں۔

تاہم، یہ ہمیشہ واضح نہیں ہوتا کہ آیا ہم یہ نتیجہ اخذ کر سکتے ہیں۔ اوپر کی بحث سے ہم جانتے ہیں کہ ہر اوسط کے ساتھ ایک متعلقہ اعتماد وقفہ ہوتا ہے، اور اس فرق کو محض ایک شماریاتی غلطی سمجھا جا سکتا ہے۔ ہمیں اپنے مفروضے کو جانچنے کے لیے کچھ زیادہ رسمی طریقہ کی ضرورت ہے۔

آئیے فرسٹ اور سیکنڈ بیس مین کے قد کے لیے اعتماد وقفے الگ الگ حساب کرتے ہیں:

اعتماد	فرسٹ بیس مین	سیکنڈ بیس مین
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

ہم دیکھ سکتے ہیں کہ کسی بھی اعتماد کے تحت وقفے ایک دوسرے سے اوورلیپ نہیں کرتے۔ یہ ہمارے مفروضے کو ثابت کرتا ہے کہ فرسٹ بیس مین سیکنڈ بیس مین سے زیادہ قد والے ہیں۔

زیادہ رسمی طور پر، مسئلہ جو ہم حل کر رہے ہیں وہ یہ دیکھنا ہے کہ دو احتمال تقسیم ایک جیسی ہیں، یا کم از کم ان کے پیرامیٹرز ایک جیسے ہیں۔ تقسیم کے لحاظ سے، ہمیں اس کے لیے مختلف ٹیسٹ استعمال کرنے کی ضرورت ہے۔ اگر ہمیں معلوم ہو کہ ہماری تقسیم نارمل ہے، تو ہم طالب علم ٹی-ٹیسٹ کا اطلاق کر سکتے ہیں۔

طالب علم ٹی-ٹیسٹ میں، ہم نام نہاد t-value کا حساب لگاتے ہیں، جو اوسط کے فرق کو ظاہر کرتا ہے، انحراف کو مدنظر رکھتے ہوئے۔ یہ دکھایا گیا ہے کہ t-value طالب علم کی تقسیم کی پیروی کرتا ہے، جو ہمیں دیے گئے اعتماد سطح p کے لیے حد قدر حاصل کرنے کی اجازت دیتا ہے (یہ حساب کیا جا سکتا ہے، یا عددی جدولوں میں دیکھا جا سکتا ہے)۔ پھر ہم t-value کو اس حد سے موازنہ کرتے ہیں تاکہ مفروضے کو منظور یا مسترد کریں۔

Python میں، ہم SciPy پیکیج استعمال کر سکتے ہیں، جس میں ttest_ind فنکشن شامل ہے (بہت سے دیگر مفید شماریاتی فنکشنز کے علاوہ!)۔ یہ ہمارے لیے t-value کا حساب لگاتا ہے، اور اعتماد p-value کا ریورس لک اپ بھی کرتا ہے، تاکہ ہم صرف اعتماد کو دیکھ کر نتیجہ اخذ کر سکیں۔

مثال کے طور پر، فرسٹ اور سیکنڈ بیس مین کے قد کے موازنہ سے ہمیں درج ذیل نتائج ملتے ہیں:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

ہمارے معاملے میں، p-value بہت کم ہے، جس کا مطلب ہے کہ فرسٹ بیس مین کے زیادہ قد ہونے کے حق میں مضبوط ثبوت موجود ہیں۔

مفروضہ ٹیسٹنگ کے دیگر مختلف اقسام بھی ہیں، جیسے:

یہ ثابت کرنا کہ دیا گیا نمونہ کسی تقسیم کی پیروی کرتا ہے۔ ہمارے معاملے میں ہم نے فرض کیا ہے کہ قد نارمل تقسیم شدہ ہیں، لیکن اس کی رسمی شماریاتی تصدیق کی ضرورت ہے۔
یہ ثابت کرنا کہ نمونے کی اوسط قدر کسی پہلے سے طے شدہ قدر کے مطابق ہے۔
مختلف نمونوں کی اوسط کا موازنہ کرنا (مثلاً مختلف عمر کے گروپوں میں خوشی کی سطح میں فرق کیا ہے)

بڑے نمبروں کا قانون اور مرکزی حد نظریہ

نارمل تقسیم اتنی اہم ہونے کی ایک وجہ مرکزی حد نظریہ ہے۔ فرض کریں کہ ہمارے پاس آزاد N قدروں X₁, ..., X_N کا بڑا نمونہ ہے، جو کسی بھی تقسیم سے لیا گیا ہے جس کی اوسط μ اور انحراف σ² ہے۔ پھر، کافی بڑے N کے لیے (دوسرے الفاظ میں، جب N→∞)، اوسط Σ_iX_i نارمل تقسیم شدہ ہوگا، جس کی اوسط μ اور انحراف σ²/N ہوگا۔

مرکزی حد نظریہ کو دوسرے طریقے سے بیان کیا جا سکتا ہے کہ قطع نظر تقسیم کے، جب آپ کسی تصادفی متغیر قدروں کے مجموعے کی اوسط کا حساب لگاتے ہیں تو آپ نارمل تقسیم کے ساتھ ختم ہوتے ہیں۔

مرکزی حد نظریہ سے یہ بھی معلوم ہوتا ہے کہ، جب N→∞، نمونے کی اوسط کے μ کے برابر ہونے کا امکان 1 بن جاتا ہے۔ یہ بڑے نمبروں کا قانون کے نام سے جانا جاتا ہے۔

کوورینس اور تعلق

ڈیٹا سائنس کا ایک کام ڈیٹا کے درمیان تعلقات تلاش کرنا ہے۔ ہم کہتے ہیں کہ دو سلسلے تعلق رکھتے ہیں جب وہ ایک ہی وقت میں ایک جیسا رویہ ظاہر کرتے ہیں، یعنی وہ یا تو ایک ساتھ بڑھتے/گرتے ہیں، یا ایک سلسلہ بڑھتا ہے جب دوسرا گرتا ہے اور اس کے برعکس۔ دوسرے الفاظ میں، دو سلسلوں کے درمیان کچھ تعلق معلوم ہوتا ہے۔

تعلق ضروری نہیں کہ دو سلسلوں کے درمیان سببی تعلق کی نشاندہی کرے؛ کبھی کبھی دونوں متغیرات کسی بیرونی وجہ پر منحصر ہو سکتے ہیں، یا یہ محض اتفاقیہ ہو سکتا ہے کہ دونوں سلسلے تعلق رکھتے ہیں۔ تاہم، مضبوط ریاضیاتی تعلق اس بات کی اچھی نشاندہی ہے کہ دو متغیرات کسی نہ کسی طرح جڑے ہوئے ہیں۔

ریاضیاتی طور پر، دو تصادفی متغیرات کے درمیان تعلق ظاہر کرنے والا بنیادی تصور کوورینس ہے، جسے اس طرح حساب کیا جاتا ہے: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]۔ ہم دونوں متغیرات کے ان کی اوسط قدروں سے انحراف کا حساب لگاتے ہیں، اور پھر ان انحرافات کی پیداوار لیتے ہیں۔ اگر دونوں متغیرات ایک ساتھ انحراف کرتے ہیں، تو پیداوار ہمیشہ ایک مثبت قدر ہوگی، جو مثبت کوورینس میں شامل ہوگی۔ اگر دونوں متغیرات غیر مطابقت سے انحراف کرتے ہیں (یعنی ایک اوسط سے نیچے گرتا ہے جب دوسرا اوسط سے اوپر بڑھتا ہے)، تو ہمیں ہمیشہ منفی نمبر ملیں گے، جو منفی کوورینس میں شامل ہوں گے۔ اگر انحرافات غیر متعلق ہوں، تو وہ تقریباً صفر میں شامل ہوں گے۔

کوورینس کی مطلق قدر ہمیں یہ نہیں بتاتی کہ تعلق کتنا بڑا ہے، کیونکہ یہ اصل قدروں کی شدت پر منحصر ہے۔ اسے معمول پر لانے کے لیے، ہم کوورینس کو دونوں متغیرات کے معیاری انحراف سے تقسیم کر سکتے ہیں، تاکہ تعلق حاصل ہو۔ اچھی بات یہ ہے کہ تعلق ہمیشہ [-1,1] کی حد میں ہوتا ہے، جہاں 1 قدروں کے درمیان مضبوط مثبت تعلق کی نشاندہی کرتا ہے، -1 - مضبوط منفی تعلق، اور 0 - کوئی تعلق نہیں (متغیرات آزاد ہیں)۔

مثال: ہم بیس بال کھلاڑیوں کے وزن اور قد کے درمیان تعلق کا حساب لگا سکتے ہیں:

print(np.corrcoef(weights,heights))

نتیجے کے طور پر، ہمیں تعلق میٹرکس اس طرح ملتا ہے:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

تعلق میٹرکس C کسی بھی تعداد کے ان پٹ سلسلوں S₁, ..., S_n کے لیے حساب کیا جا سکتا ہے۔ C_ij کی قدر S_i اور S_j کے درمیان تعلق ہے، اور قطر کے عناصر ہمیشہ 1 ہوتے ہیں (جو S_i کی خود تعلق بھی ہے)۔

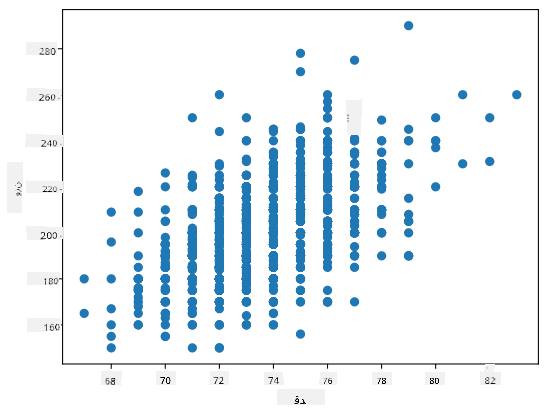
ہمارے معاملے میں، قدر 0.53 اس بات کی نشاندہی کرتی ہے کہ کسی شخص کے وزن اور قد کے درمیان کچھ تعلق ہے۔ ہم ایک قدر کے خلاف دوسرے کی اسکیٹر پلاٹ بھی بنا سکتے ہیں تاکہ تعلق کو بصری طور پر دیکھ سکیں:

تعلق اور کوورینس کی مزید مثالیں ساتھ والے نوٹ بک میں مل سکتی ہیں۔

نتیجہ

اس سیکشن میں، ہم نے سیکھا:

ڈیٹا کی بنیادی شماریاتی خصوصیات، جیسے اوسط، انحراف، موڈ اور کوارٹائلز
تصادفی متغیرات کی مختلف تقسیم، بشمول نارمل تقسیم
مختلف خصوصیات کے درمیان تعلق کیسے تلاش کریں
کچھ مفروضوں کو ثابت کرنے کے لیے ریاضی اور شماریات کے مضبوط آلات کا استعمال کیسے کریں
دیے گئے ڈیٹا نمونے کے لیے تصادفی متغیر کے اعتماد وقفے کیسے حساب کریں

جبکہ یہ احتمال اور شماریات کے اندر موجود موضوعات کی مکمل فہرست نہیں ہے، یہ اس کورس میں آپ کو اچھی شروعات دینے کے لیے کافی ہونا چاہیے۔

🚀 چیلنج

نوٹ بک میں دیے گئے نمونے کے کوڈ کا استعمال کریں تاکہ دیگر مفروضوں کو ٹیسٹ کریں:

فرسٹ بیس مین سیکنڈ بیس مین سے زیادہ عمر کے ہیں۔
فرسٹ بیس مین تھرڈ بیس مین سے زیادہ قد والے ہیں۔
شارٹ اسٹاپ سیکنڈ بیس مین سے زیادہ قد والے ہیں۔

لیکچر کے بعد کوئز

جائزہ اور خود مطالعہ

احتمال اور شماریات ایک اتنا وسیع موضوع ہے کہ یہ اپنے کورس کا مستحق ہے۔ اگر آپ نظریہ میں مزید گہرائی میں جانا چاہتے ہیں، تو آپ درج ذیل کتابوں کو پڑھنا جاری رکھ سکتے ہیں:

کارلوس فرنانڈیز-گرینڈا نیویارک یونیورسٹی سے، کے عظیم لیکچر نوٹس Probability and Statistics for Data Science (آن لائن دستیاب)
پیٹر اور اینڈریو بروس۔ عملی شماریات برائے ڈیٹا سائنسدان۔ [R میں نمونہ کوڈ]۔
جیمز ڈی. ملر۔ ڈیٹا سائنس کے لیے شماریات [R میں نمونہ کوڈ]۔

اسائنمنٹ

چھوٹا ذیابیطس مطالعہ

کریڈٹس

یہ سبق دمیتری سوشنیکوف کے ♥️ کے ساتھ تحریر کیا گیا ہے۔

ڈس کلیمر:
یہ دستاویز AI ترجمہ سروس Co-op Translator کا استعمال کرتے ہوئے ترجمہ کی گئی ہے۔ ہم درستگی کے لیے پوری کوشش کرتے ہیں، لیکن براہ کرم آگاہ رہیں کہ خودکار ترجمے میں غلطیاں یا عدم درستگی ہو سکتی ہیں۔ اصل دستاویز کو اس کی اصل زبان میں مستند ذریعہ سمجھا جانا چاہیے۔ اہم معلومات کے لیے، پیشہ ور انسانی ترجمہ کی سفارش کی جاتی ہے۔ اس ترجمے کے استعمال سے پیدا ہونے والی کسی بھی غلط فہمی یا غلط تشریح کے لیے ہم ذمہ دار نہیں ہیں۔

35 KiB Raw Permalink Blame History Unescape Escape