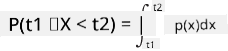50 KiB

Raw Permalink Blame History Unescape Escape

บทนำสั้น ๆ เกี่ยวกับสถิติและความน่าจะเป็น


สถิติและความน่าจะเป็น - Sketchnote โดย @nitya

ทฤษฎีสถิติและความน่าจะเป็นเป็นสองสาขาที่เกี่ยวข้องกันอย่างมากในคณิตศาสตร์ และมีความสำคัญอย่างยิ่งต่อวิทยาศาสตร์ข้อมูล แม้ว่าเราจะสามารถทำงานกับข้อมูลได้โดยไม่ต้องมีความรู้ทางคณิตศาสตร์ลึกซึ้ง แต่การมีความเข้าใจพื้นฐานบางอย่างก็ยังดีกว่า ที่นี่เราจะนำเสนอการแนะนำสั้น ๆ ที่จะช่วยให้คุณเริ่มต้นได้

แบบทดสอบก่อนการบรรยาย

ความน่าจะเป็นและตัวแปรสุ่ม

ความน่าจะเป็น คือค่าระหว่าง 0 ถึง 1 ที่แสดงถึงความเป็นไปได้ของ เหตุการณ์ โดยนิยามเป็นจำนวนผลลัพธ์ที่เป็นบวก (ที่นำไปสู่เหตุการณ์) หารด้วยจำนวนผลลัพธ์ทั้งหมด โดยที่ผลลัพธ์ทั้งหมดมีความน่าจะเป็นเท่ากัน ตัวอย่างเช่น เมื่อเราทอยลูกเต๋า ความน่าจะเป็นที่เราจะได้เลขคู่คือ 3/6 = 0.5

เมื่อเราพูดถึงเหตุการณ์ เราใช้ ตัวแปรสุ่ม ตัวอย่างเช่น ตัวแปรสุ่มที่แสดงถึงตัวเลขที่ได้จากการทอยลูกเต๋าจะมีค่าตั้งแต่ 1 ถึง 6 ชุดตัวเลขตั้งแต่ 1 ถึง 6 เรียกว่า พื้นที่ตัวอย่าง เราสามารถพูดถึงความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่าหนึ่งค่า เช่น P(X=3)=1/6

ตัวแปรสุ่มในตัวอย่างก่อนหน้านี้เรียกว่า ตัวแปรสุ่มแบบไม่ต่อเนื่อง เพราะมีพื้นที่ตัวอย่างที่นับได้ กล่าวคือมีค่าที่แยกกันและสามารถระบุได้ มีกรณีที่พื้นที่ตัวอย่างเป็นช่วงของตัวเลขจริง หรือชุดตัวเลขจริงทั้งหมด ตัวแปรเหล่านี้เรียกว่า ตัวแปรสุ่มแบบต่อเนื่อง ตัวอย่างที่ดีคือเวลาที่รถบัสมาถึง

การแจกแจงความน่าจะเป็น

ในกรณีของตัวแปรสุ่มแบบไม่ต่อเนื่อง การอธิบายความน่าจะเป็นของแต่ละเหตุการณ์ทำได้ง่ายโดยใช้ฟังก์ชัน P(X) สำหรับแต่ละค่าจากพื้นที่ตัวอย่าง S ฟังก์ชันจะให้ค่าระหว่าง 0 ถึง 1 โดยผลรวมของค่าทั้งหมดของ P(X=s) สำหรับทุกเหตุการณ์จะเท่ากับ 1

การแจกแจงแบบไม่ต่อเนื่องที่รู้จักกันดีที่สุดคือ การแจกแจงแบบสม่ำเสมอ ซึ่งมีพื้นที่ตัวอย่างที่มีองค์ประกอบ N โดยมีความน่าจะเป็นเท่ากัน 1/N สำหรับแต่ละองค์ประกอบ

การอธิบายการแจกแจงความน่าจะเป็นของตัวแปรแบบต่อเนื่องนั้นยากกว่า โดยค่าจะถูกดึงมาจากช่วง [a,b] หรือชุดตัวเลขจริงทั้งหมด ℝ ลองพิจารณากรณีเวลาที่รถบัสมาถึง ในความเป็นจริง สำหรับเวลาที่มาถึง t ที่แน่นอน ความน่าจะเป็นที่รถบัสจะมาถึงเวลานั้นคือ 0!

ตอนนี้คุณรู้แล้วว่าเหตุการณ์ที่มีความน่าจะเป็น 0 สามารถเกิดขึ้นได้ และเกิดขึ้นบ่อยมาก! อย่างน้อยก็ทุกครั้งที่รถบัสมาถึง!

เราสามารถพูดถึงความน่าจะเป็นที่ตัวแปรจะอยู่ในช่วงค่าที่กำหนด เช่น P(t₁≤X<t₂) ในกรณีนี้ การแจกแจงความน่าจะเป็นจะถูกอธิบายโดย ฟังก์ชันความหนาแน่นของความน่าจะเป็น p(x) โดยที่

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

การแจกแจงแบบต่อเนื่องที่เป็นคู่ของการแจกแจงแบบสม่ำเสมอเรียกว่า การแจกแจงแบบสม่ำเสมอต่อเนื่อง ซึ่งถูกนิยามในช่วงจำกัด ความน่าจะเป็นที่ค่าของ X จะอยู่ในช่วงความยาว l จะเป็นสัดส่วนกับ l และเพิ่มขึ้นจนถึง 1

การแจกแจงที่สำคัญอีกแบบหนึ่งคือ การแจกแจงแบบปกติ ซึ่งเราจะพูดถึงรายละเอียดเพิ่มเติมด้านล่าง

ค่าเฉลี่ย ความแปรปรวน และส่วนเบี่ยงเบนมาตรฐาน

สมมติว่าเราดึงตัวอย่าง n ตัวอย่างของตัวแปรสุ่ม X: x₁, x₂, ..., x_n เราสามารถนิยาม ค่าเฉลี่ย (หรือ ค่าเฉลี่ยเลขคณิต) ของลำดับในแบบดั้งเดิมได้เป็น (x₁+x₂+x_n)/n เมื่อเราขยายขนาดตัวอย่าง (เช่น นำไปสู่ขีดจำกัด n→∞) เราจะได้ค่าเฉลี่ย (เรียกอีกอย่างว่า ค่าคาดหวัง) ของการแจกแจง เราจะใช้สัญลักษณ์ E(x) แทนค่าคาดหวัง

สามารถแสดงให้เห็นได้ว่า สำหรับการแจกแจงแบบไม่ต่อเนื่องใด ๆ ที่มีค่า {x₁, x₂, ..., x_N} และความน่าจะเป็นที่สอดคล้องกัน p₁, p₂, ..., p_N ค่าคาดหวังจะเท่ากับ E(X)=x₁p₁+x₂p₂+...+x_Np_N

เพื่อระบุว่าค่าต่าง ๆ กระจายตัวออกไปมากน้อยเพียงใด เราสามารถคำนวณความแปรปรวน σ² = ∑(x_i - μ)²/n โดยที่ μ คือค่าเฉลี่ยของลำดับ ค่าของ σ เรียกว่า ส่วนเบี่ยงเบนมาตรฐาน และ σ² เรียกว่า ความแปรปรวน

ฐานนิยม มัธยฐาน และควอร์ไทล์

บางครั้ง ค่าเฉลี่ยไม่สามารถแสดงถึงค่าที่ "เป็นตัวแทน" ของข้อมูลได้อย่างเหมาะสม ตัวอย่างเช่น เมื่อมีค่าที่สุดโต่งบางค่าที่อยู่นอกช่วงอย่างสิ้นเชิง ค่าดังกล่าวสามารถส่งผลต่อค่าเฉลี่ยได้ ตัวบ่งชี้ที่ดีอีกตัวหนึ่งคือ มัธยฐาน ซึ่งเป็นค่าที่ครึ่งหนึ่งของจุดข้อมูลต่ำกว่าค่านั้น และอีกครึ่งหนึ่งสูงกว่าค่านั้น

เพื่อช่วยให้เราเข้าใจการแจกแจงของข้อมูล การพูดถึง ควอร์ไทล์ มีประโยชน์:

ควอร์ไทล์แรก หรือ Q1 คือค่าที่ 25% ของข้อมูลต่ำกว่าค่านั้น
ควอร์ไทล์ที่สาม หรือ Q3 คือค่าที่ 75% ของข้อมูลต่ำกว่าค่านั้น

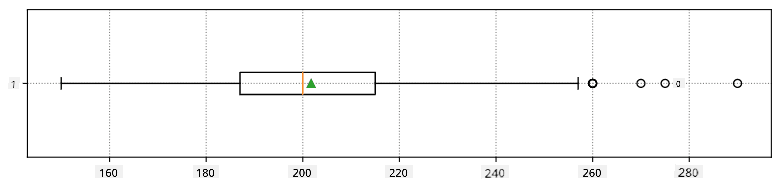
เราสามารถแสดงความสัมพันธ์ระหว่างมัธยฐานและควอร์ไทล์ในแผนภาพที่เรียกว่า กล่องแผนภาพ:

ที่นี่เรายังคำนวณ ช่วงควอร์ไทล์ IQR=Q3-Q1 และค่าที่เรียกว่า ค่าผิดปกติ - ค่าที่อยู่นอกขอบเขต [Q1-1.5IQR,Q3+1.5IQR]

สำหรับการแจกแจงที่มีจำนวนค่าที่เป็นไปได้จำกัด ค่า "ตัวแทน" ที่ดีคือค่าที่ปรากฏบ่อยที่สุด ซึ่งเรียกว่า ฐานนิยม โดยมักใช้กับข้อมูลประเภทหมวดหมู่ เช่น สี ลองพิจารณาสถานการณ์ที่เรามีกลุ่มคนสองกลุ่ม - กลุ่มที่ชอบสีแดงอย่างมาก และกลุ่มที่ชอบสีน้ำเงิน หากเรารหัสสีด้วยตัวเลข ค่าเฉลี่ยสำหรับสีที่ชอบจะอยู่ในช่วงสีส้ม-เขียว ซึ่งไม่ได้แสดงถึงความชอบที่แท้จริงของทั้งสองกลุ่ม อย่างไรก็ตาม ฐานนิยมจะเป็นสีใดสีหนึ่ง หรือทั้งสองสี หากจำนวนคนที่เลือกสีเหล่านั้นเท่ากัน (ในกรณีนี้เราเรียกตัวอย่างว่า หลายฐานนิยม)

ข้อมูลในโลกจริง

เมื่อเราวิเคราะห์ข้อมูลจากชีวิตจริง ข้อมูลเหล่านั้นมักไม่ใช่ตัวแปรสุ่มในแง่ที่ว่าเราไม่ได้ทำการทดลองที่มีผลลัพธ์ที่ไม่ทราบล่วงหน้า ตัวอย่างเช่น ลองพิจารณาทีมนักเบสบอล และข้อมูลร่างกายของพวกเขา เช่น ส่วนสูง น้ำหนัก และอายุ ตัวเลขเหล่านี้ไม่ใช่ตัวแปรสุ่มอย่างแท้จริง แต่เรายังสามารถใช้แนวคิดทางคณิตศาสตร์เดียวกันได้ ตัวอย่างเช่น ลำดับน้ำหนักของคนสามารถถือว่าเป็นลำดับค่าที่ดึงมาจากตัวแปรสุ่มบางตัว ด้านล่างคือลำดับน้ำหนักของนักเบสบอลจริงจาก Major League Baseball ซึ่งนำมาจาก ชุดข้อมูลนี้ (เพื่อความสะดวก มีการแสดงเพียง 20 ค่าตัวอย่างแรก):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

หมายเหตุ: หากต้องการดูตัวอย่างการทำงานกับชุดข้อมูลนี้ ลองดูที่ สมุดบันทึกที่เกี่ยวข้อง นอกจากนี้ยังมีความท้าทายหลายอย่างตลอดบทเรียนนี้ และคุณสามารถทำให้เสร็จได้โดยเพิ่มโค้ดบางส่วนลงในสมุดบันทึกนั้น หากคุณไม่แน่ใจว่าจะทำงานกับข้อมูลอย่างไร ไม่ต้องกังวล - เราจะกลับมาทำงานกับข้อมูลโดยใช้ Python ในภายหลัง หากคุณไม่ทราบวิธีการรันโค้ดใน Jupyter Notebook ลองดู บทความนี้

นี่คือกล่องแผนภาพที่แสดงค่าเฉลี่ย มัธยฐาน และควอร์ไทล์สำหรับข้อมูลของเรา:

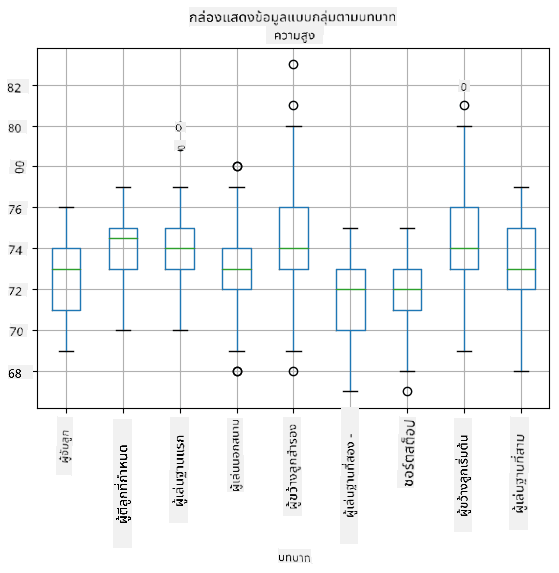
เนื่องจากข้อมูลของเรามีข้อมูลเกี่ยวกับ บทบาท ของผู้เล่นที่แตกต่างกัน เราสามารถสร้างกล่องแผนภาพตามบทบาทได้ - ซึ่งจะช่วยให้เราเข้าใจว่าค่าพารามิเตอร์แตกต่างกันอย่างไรในแต่ละบทบาท ครั้งนี้เราจะพิจารณาส่วนสูง:

แผนภาพนี้แสดงให้เห็นว่า โดยเฉลี่ยแล้ว ส่วนสูงของผู้เล่นตำแหน่งเบสแรกสูงกว่าส่วนสูงของผู้เล่นตำแหน่งเบสที่สอง ในบทเรียนนี้เราจะเรียนรู้วิธีการทดสอบสมมติฐานนี้อย่างเป็นทางการมากขึ้น และวิธีการแสดงให้เห็นว่าข้อมูลของเรามีความสำคัญทางสถิติในการแสดงผลดังกล่าว

เมื่อทำงานกับข้อมูลในโลกจริง เราถือว่าจุดข้อมูลทั้งหมดเป็นตัวอย่างที่ดึงมาจากการแจกแจงความน่าจะเป็นบางอย่าง สมมติฐานนี้ช่วยให้เราสามารถใช้เทคนิคการเรียนรู้ของเครื่องและสร้างโมเดลการทำนายที่ใช้งานได้

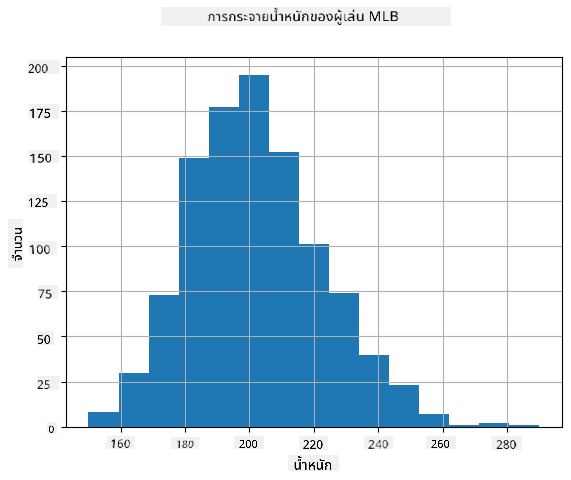
เพื่อดูว่าการแจกแจงของข้อมูลของเราเป็นอย่างไร เราสามารถสร้างกราฟที่เรียกว่า ฮิสโตแกรม แกน X จะมีจำนวนช่วงน้ำหนักที่แตกต่างกัน (เรียกว่า bins) และแกนตั้งจะแสดงจำนวนครั้งที่ตัวอย่างตัวแปรสุ่มอยู่ในช่วงที่กำหนด

จากฮิสโตแกรมนี้คุณจะเห็นว่าค่าทั้งหมดกระจุกตัวอยู่รอบ ๆ น้ำหนักเฉลี่ยบางค่า และยิ่งเราออกห่างจากน้ำหนักนั้น - น้ำหนักที่มีค่านั้นจะยิ่งพบได้น้อยลง กล่าวคือ เป็นไปได้น้อยมากที่น้ำหนักของนักเบสบอลจะต่างจากน้ำหนักเฉลี่ย ความแปรปรวนของน้ำหนักแสดงถึงขอบเขตที่น้ำหนักมีแนวโน้มที่จะต่างจากค่าเฉลี่ย

หากเรานำน้ำหนักของคนอื่นที่ไม่ใช่นักเบสบอล การแจกแจงมีแนวโน้มที่จะต่างออกไป อย่างไรก็ตาม รูปร่างของการแจกแจงจะเหมือนเดิม แต่ค่าเฉลี่ยและความแปรปรวนจะเปลี่ยนไป ดังนั้น หากเราเทรนโมเดลของเรากับนักเบสบอล มีแนวโน้มที่ผลลัพธ์จะผิดพลาดเมื่อใช้กับนักศึกษามหาวิทยาลัย เพราะการแจกแจงพื้นฐานต่างกัน

การแจกแจงแบบปกติ

การแจกแจงน้ำหนักที่เราเห็นด้านบนเป็นเรื่องปกติมาก และการวัดหลายอย่างจากโลกจริงมีรูปแบบการแจกแจงเดียวกัน แต่มีค่าเฉลี่ยและความแปรปรวนต่างกัน การแจกแจงนี้เรียกว่า การแจกแจงแบบปกติ และมีบทบาทสำคัญในสถิติ

การใช้การแจกแจงแบบปกติเป็นวิธีที่ถูกต้องในการสร้างน้ำหนักสุ่มของนักเบสบอลที่มีศักยภาพ เมื่อเรารู้ค่าเฉลี่ย mean และส่วนเบี่ยงเบนมาตรฐาน std เราสามารถสร้างตัวอย่างน้ำหนัก 1000 ตัวอย่างได้ดังนี้:

samples = np.random.normal(mean,std,1000)

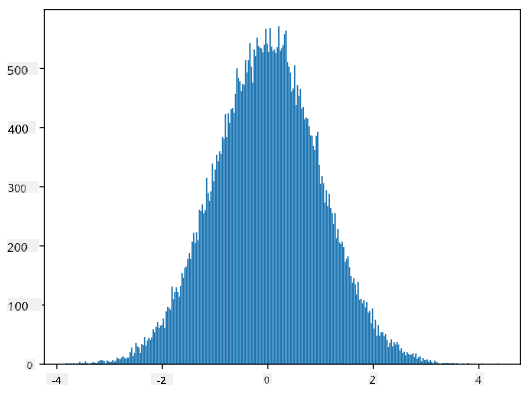
หากเราสร้างฮิสโตแกรมของตัวอย่างที่สร้างขึ้น เราจะเห็นภาพที่คล้ายกับภาพที่แสดงด้านบน และหากเราเพิ่มจำนวนตัวอย่างและจำนวน bins เราสามารถสร้างภาพการแจกแจงแบบปกติที่ใกล้เคียงกับอุดมคติมากขึ้น:

การแจกแจงแบบปกติที่มีค่าเฉลี่ย=0 และส่วนเบี่ยงเบนมาตรฐาน=1

ช่วงความเชื่อมั่น

เมื่อเราพูดถึงน้ำหนักของนักเบสบอล เราถือว่ามี ตัวแปรสุ่ม W ที่สอดคล้องกับการแจกแจงความน่าจะเป็นที่เหมาะสมของน้ำหนักของนักเบสบอลทั้งหมด (เรียกว่า ประชากร) ลำดับน้ำหนักของเราสอดคล้องกับชุดย่อยของนักเบสบอลทั้งหมดที่เราเรียกว่า ตัวอย่าง คำถามที่น่าสนใจคือ เราสามารถทราบพารามิเตอร์ของการแจกแจงของ W ได้หรือไม่ เช่น ค่าเฉลี่ยและความแปรปรวนของประชากร?

คำตอบที่ง่ายที่สุดคือการคำนวณค่าเฉลี่ยและความแปรปรวนของตัวอย่างของเรา อย่างไรก็ตาม อาจเกิดขึ้นได้ว่าตัวอย่างสุ่มของเราไม่ได้แสดงถึงประชากรทั้งหมดอย่างถูกต้อง ดังนั้นจึงสมเหตุสมผลที่จะพูดถึง ช่วงความเชื่อมั่น

ช่วงความเชื่อมั่น คือการประมาณค่ามัชฌิมจริงของประชากรโดยอ้างอิงจากตัวอย่างของเรา ซึ่งมีความแม่นยำในระดับความน่าจะเป็นที่กำหนด (หรือ ระดับความเชื่อมั่น) สมมติว่าเรามีตัวอย่าง X₁, ..., X_n จากการแจกแจงของเรา ทุกครั้งที่เราดึงตัวอย่างจากการแจกแจง เราจะได้ค่ามัชฌิม (mean) ที่แตกต่างกัน μ ดังนั้น μ สามารถถือว่าเป็นตัวแปรสุ่มได้ ช่วงความเชื่อมั่น (confidence interval) ที่มีความเชื่อมั่น p คือคู่ของค่า (L_p,R_p) ซึ่ง P(L_p≤μ≤R_p) = p หรือก็คือ ความน่าจะเป็นที่ค่ามัชฌิมที่วัดได้จะอยู่ในช่วงนี้เท่ากับ p

การคำนวณช่วงความเชื่อมั่นอย่างละเอียดเกินกว่าที่เราจะอธิบายในบทนำสั้น ๆ นี้ รายละเอียดเพิ่มเติมสามารถดูได้ที่ Wikipedia โดยสรุป เรากำหนดการแจกแจงของค่ามัชฌิมที่คำนวณได้เมื่อเทียบกับค่ามัชฌิมจริงของประชากร ซึ่งเรียกว่า การแจกแจงของ Student

ข้อเท็จจริงที่น่าสนใจ: การแจกแจงของ Student ได้รับการตั้งชื่อตามนักคณิตศาสตร์ William Sealy Gosset ซึ่งตีพิมพ์งานวิจัยของเขาภายใต้นามปากกา "Student" เขาทำงานที่โรงเบียร์ Guinness และตามหนึ่งในเรื่องเล่า นายจ้างของเขาไม่ต้องการให้สาธารณชนทราบว่าพวกเขาใช้การทดสอบทางสถิติเพื่อกำหนดคุณภาพของวัตถุดิบ

หากเราต้องการประมาณค่ามัชฌิม μ ของประชากรด้วยความเชื่อมั่น p เราจำเป็นต้องใช้ (1-p)/2-th percentile ของการแจกแจงของ Student A ซึ่งสามารถหาได้จากตาราง หรือคำนวณด้วยฟังก์ชันในซอฟต์แวร์สถิติ (เช่น Python, R เป็นต้น) จากนั้นช่วงสำหรับ μ จะถูกกำหนดโดย X±A*D/√n โดยที่ X คือค่ามัชฌิมที่ได้จากตัวอย่าง และ D คือส่วนเบี่ยงเบนมาตรฐาน

หมายเหตุ: เราไม่ได้พูดถึงแนวคิดสำคัญของ degrees of freedom ซึ่งมีความสำคัญในบริบทของการแจกแจงของ Student คุณสามารถศึกษาเพิ่มเติมได้จากหนังสือสถิติที่สมบูรณ์ยิ่งขึ้น

ตัวอย่างการคำนวณช่วงความเชื่อมั่นสำหรับน้ำหนักและส่วนสูงสามารถดูได้ใน notebook ที่แนบมา

p	ค่ามัชฌิมน้ำหนัก
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

สังเกตว่าความน่าจะเป็นของความเชื่อมั่นที่สูงขึ้น ช่วงความเชื่อมั่นจะกว้างขึ้น

การทดสอบสมมติฐาน

ในชุดข้อมูลนักเบสบอลของเรา มีบทบาทของผู้เล่นที่แตกต่างกัน ซึ่งสามารถสรุปได้ดังนี้ (ดู notebook ที่แนบมา เพื่อดูวิธีการคำนวณตารางนี้):

บทบาท	ส่วนสูง	น้ำหนัก	จำนวน
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

เราสามารถสังเกตได้ว่าค่ามัชฌิมส่วนสูงของ First Basemen สูงกว่าของ Second Basemen ดังนั้นเราอาจสรุปได้ว่า First Basemen สูงกว่า Second Basemen

ข้อความนี้เรียกว่า สมมติฐาน เพราะเราไม่ทราบว่าข้อเท็จจริงนี้เป็นจริงหรือไม่

อย่างไรก็ตาม ไม่ใช่เรื่องง่ายเสมอไปที่เราจะสรุปเช่นนี้ จากการอภิปรายข้างต้น เราทราบว่าค่ามัชฌิมแต่ละค่ามีช่วงความเชื่อมั่นที่เกี่ยวข้อง และความแตกต่างนี้อาจเป็นเพียงข้อผิดพลาดทางสถิติ เราจำเป็นต้องมีวิธีการที่เป็นทางการมากขึ้นในการทดสอบสมมติฐานของเรา

ลองคำนวณช่วงความเชื่อมั่นแยกกันสำหรับส่วนสูงของ First Basemen และ Second Basemen:

ความเชื่อมั่น	First Basemen	Second Basemen
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

เราสามารถเห็นได้ว่าในทุกระดับความเชื่อมั่น ช่วงความเชื่อมั่นไม่ทับซ้อนกัน นั่นพิสูจน์สมมติฐานของเราว่า First Basemen สูงกว่า Second Basemen

ในเชิงรูปธรรมมากขึ้น ปัญหาที่เรากำลังแก้คือการดูว่า การแจกแจงความน่าจะเป็นสองชุดเหมือนกันหรือไม่ หรืออย่างน้อยมีพารามิเตอร์เดียวกันหรือไม่ ขึ้นอยู่กับการแจกแจง เราจำเป็นต้องใช้การทดสอบที่แตกต่างกัน หากเราทราบว่าการแจกแจงของเราปกติ เราสามารถใช้ Student t-test ได้

ใน Student t-test เราคำนวณค่าที่เรียกว่า t-value ซึ่งบ่งบอกถึงความแตกต่างระหว่างค่ามัชฌิม โดยคำนึงถึงความแปรปรวน มีการแสดงให้เห็นว่า t-value ปฏิบัติตาม การแจกแจงของ Student ซึ่งช่วยให้เราหาค่าขีดจำกัดสำหรับระดับความเชื่อมั่น p (สามารถคำนวณหรือดูได้จากตารางตัวเลข) จากนั้นเราจะเปรียบเทียบ t-value กับค่าขีดจำกัดนี้เพื่อยืนยันหรือปฏิเสธสมมติฐาน

ใน Python เราสามารถใช้แพ็กเกจ SciPy ซึ่งมีฟังก์ชัน ttest_ind (นอกเหนือจากฟังก์ชันสถิติที่มีประโยชน์อื่น ๆ อีกมากมาย!) ฟังก์ชันนี้คำนวณ t-value ให้เรา และยังทำการค้นหาค่าความเชื่อมั่น p-value ย้อนกลับ ดังนั้นเราสามารถดูค่าความเชื่อมั่นเพื่อสรุปผลได้

ตัวอย่างเช่น การเปรียบเทียบส่วนสูงระหว่าง First Basemen และ Second Basemen ให้ผลลัพธ์ดังนี้:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

ในกรณีของเรา ค่า p-value ต่ำมาก หมายความว่ามีหลักฐานที่ชัดเจนสนับสนุนว่า First Basemen สูงกว่า

ยังมีสมมติฐานประเภทอื่น ๆ ที่เราอาจต้องการทดสอบ เช่น:

เพื่อพิสูจน์ว่าตัวอย่างที่กำหนดเป็นไปตามการแจกแจงบางอย่าง ในกรณีของเรา เราสมมติว่าส่วนสูงมีการแจกแจงแบบปกติ แต่ต้องการการตรวจสอบทางสถิติอย่างเป็นทางการ
เพื่อพิสูจน์ว่าค่ามัชฌิมของตัวอย่างตรงกับค่าที่กำหนดไว้ล่วงหน้า
เพื่อเปรียบเทียบค่ามัชฌิมของตัวอย่างหลายชุด (เช่น ความแตกต่างในระดับความสุขระหว่างกลุ่มอายุที่แตกต่างกัน)

กฎของจำนวนมากและทฤษฎีขีดจำกัดกลาง

หนึ่งในเหตุผลที่การแจกแจงแบบปกติมีความสำคัญคือ ทฤษฎีขีดจำกัดกลาง สมมติว่าเรามีตัวอย่างขนาดใหญ่ของค่าที่เป็นอิสระ N ค่า X₁, ..., X_N ที่สุ่มตัวอย่างจากการแจกแจงใด ๆ ที่มีค่ามัชฌิม μ และความแปรปรวน σ² จากนั้น สำหรับ N ที่ใหญ่พอ (หรือเมื่อ N→∞) ค่ามัชฌิม Σ_iX_i จะมีการแจกแจงแบบปกติ โดยมีค่ามัชฌิม μ และความแปรปรวน σ²/N

อีกวิธีหนึ่งในการตีความทฤษฎีขีดจำกัดกลางคือ ไม่ว่าการแจกแจงจะเป็นอย่างไร เมื่อคุณคำนวณค่ามัชฌิมของผลรวมของค่าตัวแปรสุ่มใด ๆ คุณจะได้การแจกแจงแบบปกติ

จากทฤษฎีขีดจำกัดกลางยังสรุปได้ว่า เมื่อ N→∞ ความน่าจะเป็นที่ค่ามัชฌิมของตัวอย่างจะเท่ากับ μ จะกลายเป็น 1 ซึ่งเรียกว่า กฎของจำนวนมาก

ความแปรปรวนร่วมและความสัมพันธ์

หนึ่งในสิ่งที่ Data Science ทำคือการค้นหาความสัมพันธ์ระหว่างข้อมูล เรากล่าวว่าลำดับสองลำดับ มีความสัมพันธ์ เมื่อพวกมันแสดงพฤติกรรมที่คล้ายกันในเวลาเดียวกัน เช่น เพิ่มขึ้น/ลดลงพร้อมกัน หรือหนึ่งลำดับเพิ่มขึ้นเมื่ออีกลำดับลดลง และในทางกลับกัน กล่าวอีกนัยหนึ่ง ดูเหมือนว่าจะมีความสัมพันธ์ระหว่างลำดับทั้งสอง

ความสัมพันธ์ไม่ได้บ่งบอกถึงความสัมพันธ์เชิงสาเหตุระหว่างลำดับทั้งสองเสมอไป บางครั้งตัวแปรทั้งสองอาจขึ้นอยู่กับสาเหตุภายนอก หรืออาจเป็นเพียงความบังเอิญที่ลำดับทั้งสองมีความสัมพันธ์กัน อย่างไรก็ตาม ความสัมพันธ์ทางคณิตศาสตร์ที่แข็งแกร่งเป็นตัวบ่งชี้ที่ดีว่าตัวแปรทั้งสองมีความเชื่อมโยงกันในบางลักษณะ

ในเชิงคณิตศาสตร์ แนวคิดหลักที่แสดงความสัมพันธ์ระหว่างตัวแปรสุ่มสองตัวคือ ความแปรปรวนร่วม ซึ่งคำนวณดังนี้: Cov(X,Y) = E[(X-E(X))(Y-E(Y))] เราคำนวณการเบี่ยงเบนของตัวแปรทั้งสองจากค่ามัชฌิมของพวกมัน และคูณผลลัพธ์ของการเบี่ยงเบนเหล่านั้น หากตัวแปรทั้งสองเบี่ยงเบนไปในทิศทางเดียวกัน ผลคูณจะเป็นค่าบวกเสมอ ซึ่งจะรวมกันเป็นความแปรปรวนร่วมที่เป็นบวก หากตัวแปรทั้งสองเบี่ยงเบนไม่พร้อมกัน (เช่น หนึ่งลดลงต่ำกว่าค่าเฉลี่ยเมื่ออีกตัวเพิ่มขึ้นสูงกว่าค่าเฉลี่ย) เราจะได้ค่าลบเสมอ ซึ่งจะรวมกันเป็นความแปรปรวนร่วมที่เป็นลบ หากการเบี่ยงเบนไม่ขึ้นอยู่กัน พวกมันจะรวมกันเป็นศูนย์โดยประมาณ

ค่าความแปรปรวนร่วมในเชิงสัมบูรณ์ไม่ได้บอกเรามากนักเกี่ยวกับขนาดของความสัมพันธ์ เพราะมันขึ้นอยู่กับขนาดของค่าจริง เพื่อทำให้เป็นมาตรฐาน เราสามารถหารความแปรปรวนร่วมด้วยส่วนเบี่ยงเบนมาตรฐานของตัวแปรทั้งสอง เพื่อให้ได้ ความสัมพันธ์ ข้อดีคือความสัมพันธ์จะอยู่ในช่วง [-1,1] เสมอ โดยที่ 1 บ่งบอกถึงความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างค่า -1 บ่งบอกถึงความสัมพันธ์เชิงลบที่แข็งแกร่ง และ 0 บ่งบอกว่าไม่มีความสัมพันธ์เลย (ตัวแปรเป็นอิสระ)

ตัวอย่าง: เราสามารถคำนวณความสัมพันธ์ระหว่างน้ำหนักและส่วนสูงของนักเบสบอลจากชุดข้อมูลที่กล่าวถึงข้างต้น:

print(np.corrcoef(weights,heights))

ผลลัพธ์ที่ได้คือ เมทริกซ์ความสัมพันธ์ ดังนี้:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

เมทริกซ์ความสัมพันธ์ C สามารถคำนวณได้สำหรับลำดับข้อมูลใด ๆ S₁, ..., S_n ค่า C_ij คือความสัมพันธ์ระหว่าง S_i และ S_j และองค์ประกอบในแนวทแยงมุมจะเป็น 1 เสมอ (ซึ่งก็คือความสัมพันธ์ของ S_i กับตัวมันเอง)

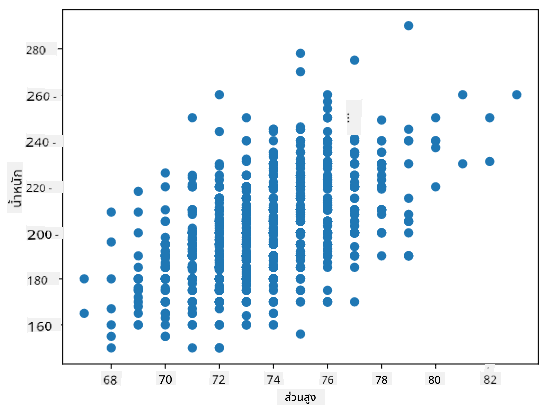
ในกรณีของเรา ค่า 0.53 บ่งบอกว่ามีความสัมพันธ์บางอย่างระหว่างน้ำหนักและส่วนสูงของบุคคล เราสามารถสร้างกราฟกระจายของค่าหนึ่งเทียบกับอีกค่าหนึ่งเพื่อดูความสัมพันธ์ในเชิงภาพ:

ตัวอย่างเพิ่มเติมของความสัมพันธ์และความแปรปรวนร่วมสามารถดูได้ใน notebook ที่แนบมา

สรุป

ในส่วนนี้ เราได้เรียนรู้:

คุณสมบัติทางสถิติพื้นฐานของข้อมูล เช่น ค่ามัชฌิม ความแปรปรวน มัธยฐาน และควอไทล์
การแจกแจงของตัวแปรสุ่มที่แตกต่างกัน รวมถึงการแจกแจงแบบปกติ
วิธีหาความสัมพันธ์ระหว่างคุณสมบัติต่าง ๆ
วิธีใช้คณิตศาสตร์และสถิติอย่างถูกต้องเพื่อพิสูจน์สมมติฐานบางอย่าง
วิธีคำนวณช่วงความเชื่อมั่นสำหรับตัวแปรสุ่มจากตัวอย่างข้อมูล

แม้ว่านี่จะไม่ใช่รายการหัวข้อที่ครบถ้วนในความน่าจะเป็นและสถิติ แต่ก็ควรเพียงพอที่จะให้คุณเริ่มต้นในหลักสูตรนี้ได้

🚀 ความท้าทาย

ใช้โค้ดตัวอย่างใน notebook เพื่อทดสอบสมมติฐานอื่น ๆ ดังนี้:

First Basemen มีอายุมากกว่า Second Basemen
First Basemen สูงกว่า Third Basemen
Shortstops สูงกว่า Second Basemen

แบบทดสอบหลังการบรรยาย

การทบทวนและการศึกษาด้วยตนเอง

ความน่าจะเป็นและสถิติเป็นหัวข้อที่กว้างขวางมากจนสมควรมีหลักสูตรของตัวเอง หากคุณสนใจที่จะศึกษาทฤษฎีให้ลึกซึ้งยิ่งขึ้น คุณอาจต้องการอ่านหนังสือดังต่อไปนี้:

Carlos Fernandez-Granda จากมหาวิทยาลัยนิวยอร์กมีบันทึกการบรรยายที่ยอดเยี่ยม Probability and Statistics for Data Science (มีให้บริการออนไลน์)
Peter and Andrew Bruce. Practical Statistics for Data Scientists. [โค้ดตัวอย่างใน R]
James D. Miller. Statistics for Data Science [โค้ดตัวอย่างใน R]

การบ้าน

Small Diabetes Study

เครดิต

บทเรียนนี้เขียนขึ้นด้วย ♥️ โดย Dmitry Soshnikov

ข้อจำกัดความรับผิดชอบ:
เอกสารนี้ได้รับการแปลโดยใช้บริการแปลภาษา AI Co-op Translator แม้ว่าเราจะพยายามอย่างเต็มที่เพื่อให้การแปลมีความถูกต้อง แต่โปรดทราบว่าการแปลอัตโนมัติอาจมีข้อผิดพลาดหรือความไม่แม่นยำ เอกสารต้นฉบับในภาษาต้นทางควรถือเป็นแหล่งข้อมูลที่เชื่อถือได้ สำหรับข้อมูลที่มีความสำคัญ แนะนำให้ใช้บริการแปลภาษามนุษย์ที่เป็นมืออาชีพ เราไม่รับผิดชอบต่อความเข้าใจผิดหรือการตีความที่ผิดพลาดซึ่งเกิดจากการใช้การแปลนี้

50 KiB Raw Permalink Blame History Unescape Escape