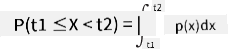20 KiB

Raw Permalink Blame History Unescape Escape

統計學與機率的簡介


統計學與機率 - Sketchnote by @nitya

統計學與機率理論是數學中兩個高度相關的領域，對於數據科學非常重要。雖然在沒有深入數學知識的情況下也可以處理數據，但了解一些基本概念仍然是有益的。在這裡，我們將提供一個簡短的介紹，幫助你入門。

課前測驗

機率與隨機變數

機率是介於 0 和 1 之間的一個數字，用來表示某個事件發生的可能性。它被定義為正面結果（導致事件發生的結果）的數量，除以所有可能結果的總數，前提是所有結果的可能性相等。例如，當我們擲骰子時，得到偶數的機率是 3/6 = 0.5。

當我們談論事件時，我們使用 隨機變數。例如，表示擲骰子時得到的數字的隨機變數，其值範圍是 1 到 6。1 到 6 的集合被稱為 樣本空間。我們可以討論隨機變數取某個值的機率，例如 P(X=3)=1/6。

上述例子中的隨機變數被稱為 離散型，因為它有一個可數的樣本空間，也就是說可以列舉出單獨的值。有些情況下，樣本空間是一個實數範圍，或者是整個實數集合。這樣的變數被稱為 連續型。一個很好的例子是公車到達的時間。

機率分佈

對於離散型隨機變數，我們可以用一個函數 P(X) 來描述每個事件的機率。對於樣本空間 S 中的每個值 s，它會給出一個介於 0 和 1 之間的數字，並且所有事件的 P(X=s) 值的總和為 1。

最著名的離散分佈是 均勻分佈，其中樣本空間有 N 個元素，每個元素的機率相等，為 1/N。

描述連續型變數的機率分佈則更困難，這些變數的值來自某個區間 [a,b] 或整個實數集合 ℝ。以公車到達時間為例，事實上，公車在某個精確時間 t 到達的機率是 0！

現在你知道了機率為 0 的事件是會發生的，而且非常頻繁！至少每次公車到達時都是如此！

我們只能討論變數落在某個值區間內的機率，例如 P(t₁≤X<t₂)。在這種情況下，機率分佈由 機率密度函數 p(x) 描述，其公式如下：

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

連續型均勻分佈是均勻分佈的連續版本，定義在有限區間內。變數 X 落入某個區間的機率與區間長度 l 成正比，並且最大為 1。

另一個重要的分佈是 正態分佈，我們將在下面詳細討論。

平均值、方差與標準差

假設我們抽取了 n 個隨機變數 X 的樣本：x₁, x₂, ..., x_n。我們可以用傳統方式定義序列的 平均值（或 算術平均值），公式為 (x₁+x₂+x_n)/n。當樣本數量增加（即 n→∞），我們將得到分佈的平均值（也稱為 期望值）。我們用 E(x) 表示期望值。

可以證明，對於任何離散分佈，其值為 {x₁, x₂, ..., x_N}，對應的機率為 p₁, p₂, ..., p_N，期望值為 E(X)=x₁p₁+x₂p₂+...+x_Np_N。

為了衡量數值的分散程度，我們可以計算方差 σ² = ∑(x_i - μ)²/n，其中 μ 是序列的平均值。σ 被稱為 標準差，而 σ² 被稱為方差。

眾數、中位數與四分位數

有時候，平均值並不能充分代表數據的「典型」值。例如，當有一些極端值完全超出範圍時，它們可能會影響平均值。另一個很好的指標是 中位數，即一個值，使得一半的數據點低於它，另一半高於它。

為了幫助我們理解數據的分佈，討論 四分位數 是有幫助的：

第一四分位數（Q1）：25% 的數據低於該值
第三四分位數（Q3）：75% 的數據低於該值

我們可以用一個叫做 盒形圖 的圖表來表示中位數與四分位數之間的關係：

在這裡，我們還計算了 四分位距 IQR=Q3-Q1，以及所謂的 離群值——位於 [Q1-1.5IQR,Q3+1.5IQR] 範圍之外的值。

對於包含少量可能值的有限分佈，一個好的「典型」值是出現最頻繁的值，稱為眾數。它通常應用於分類數據，例如顏色。考慮以下情況：有兩組人，一組強烈偏好紅色，另一組偏好藍色。如果我們用數字編碼顏色，最喜歡的顏色的平均值可能會落在橙色或綠色範圍，這並不能反映任何一組的實際偏好。然而，眾數可能是其中一種顏色，或者是兩種顏色（如果投票人數相等，在這種情況下我們稱樣本為 多眾數）。

真實世界數據

當我們分析真實世界的數據時，它們通常不是隨機變數，因為我們並未進行未知結果的實驗。例如，考慮一組棒球隊員及其身體數據，如身高、體重和年齡。這些數字並不完全是隨機的，但我們仍然可以應用相同的數學概念。例如，一組人的體重可以被視為某個隨機變數的值序列。以下是來自美國職業棒球大聯盟的棒球隊員的體重序列，取自這個數據集（為方便起見，僅顯示前 20 個值）：

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

注意：要查看使用此數據集的示例，請參考配套筆記本。本課程中還有許多挑戰，你可以通過向該筆記本添加一些代碼來完成它們。如果你不確定如何操作數據，請不要擔心——我們稍後會回到使用 Python 處理數據的部分。如果你不知道如何在 Jupyter Notebook 中運行代碼，請參考這篇文章。

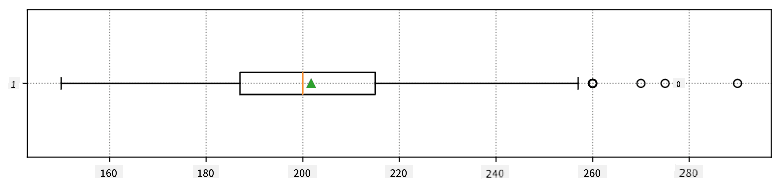
以下是顯示我們數據的平均值、中位數和四分位數的盒形圖：

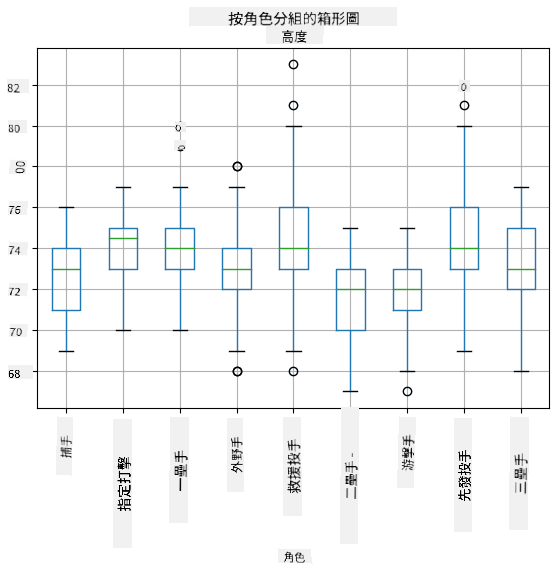
由於我們的數據包含不同球員角色的信息，我們也可以按角色繪製盒形圖——這可以幫助我們了解參數值在不同角色之間的差異。這次我們將考慮身高：

這個圖表表明，平均而言，一壘手的身高高於二壘手的身高。在本課程的後面，我們將學習如何更正式地檢驗這一假設，以及如何證明我們的數據在統計上具有顯著性。

在處理真實世界數據時，我們假設所有數據點都是從某個機率分佈中抽取的樣本。這一假設使我們能夠應用機器學習技術並構建有效的預測模型。

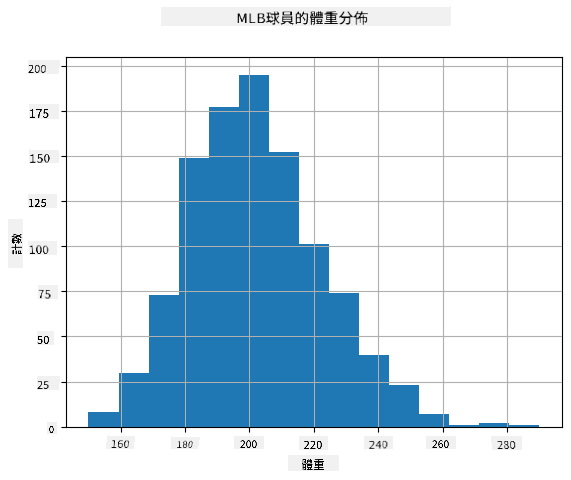
為了查看我們數據的分佈，我們可以繪製一個叫做 直方圖 的圖表。X 軸包含不同的體重區間（即分箱），Y 軸顯示隨機變數樣本落入某個區間的次數。

從這個直方圖中可以看出，所有值都集中在某個平均體重附近，距離平均體重越遠，該值出現的次數越少。也就是說，棒球隊員的體重非常接近平均體重的可能性很高。體重的方差顯示了體重與平均值可能的差異程度。

如果我們取其他人的體重，而不是棒球聯盟的球員，分佈可能會有所不同。然而，分佈的形狀會保持相同，但平均值和方差會改變。因此，如果我們在棒球隊員上訓練模型，當應用於大學學生時可能會得出錯誤的結果，因為底層分佈不同。

正態分佈

我們上面看到的體重分佈非常典型，許多來自真實世界的測量值遵循相同類型的分佈，但具有不同的平均值和方差。這種分佈被稱為 正態分佈，在統計學中具有非常重要的作用。

使用正態分佈是生成潛在棒球隊員隨機體重的正確方法。一旦我們知道平均體重 mean 和標準差 std，我們可以用以下方式生成 1000 個體重樣本：

samples = np.random.normal(mean,std,1000)

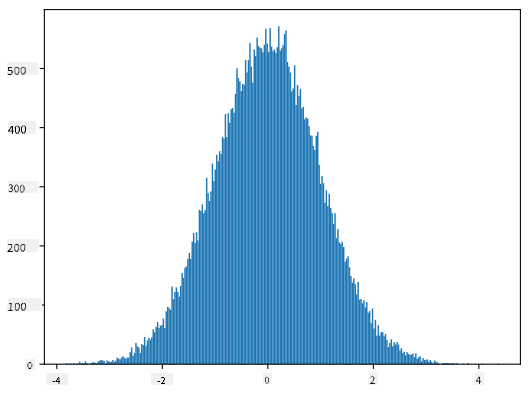
如果我們繪製生成樣本的直方圖，我們會看到與上面類似的圖像。如果我們增加樣本數量和分箱數量，我們可以生成更接近理想的正態分佈圖像：

平均值=0，標準差=1 的正態分佈

信賴區間

當我們談論棒球隊員的體重時，我們假設存在某個 隨機變數 W，它對應於所有棒球隊員體重的理想機率分佈（即母體）。我們的體重序列對應於所有棒球隊員的一個子集，稱為樣本。一個有趣的問題是，我們能否知道 W 的分佈參數，即母體的平均值和方差？

最簡單的答案是計算樣本的平均值和方差。然而，可能出現的情況是，我們的隨機樣本並不能準確代表完整的母體。因此，討論 信賴區間 是有意義的。

信賴區間 是根據我們的樣本來估計母體真實平均值的一種方法，其準確性在某一特定的概率（或稱為 信心水準）內。假設我們有一個樣本 X₁, ..., X_n 來自我們的分佈。每次從分佈中抽取樣本時，我們都會得到不同的平均值 μ。因此，μ 可以被視為一個隨機變數。一個具有置信度 p 的 置信區間 是一對值 (L_p,R_p)，使得 P(L_p≤μ≤R_p) = p，也就是說測得的平均值落在該區間內的概率等於 p。

詳細討論如何計算這些置信區間超出了我們的簡短介紹範圍。更多細節可以參考維基百科。簡而言之，我們定義了計算出的樣本平均值相對於母體真實平均值的分佈，這被稱為 學生分佈。

有趣的事實：學生分佈的名稱來自數學家 William Sealy Gosset，他以筆名 "Student" 發表了他的論文。他在健力士啤酒廠工作，根據其中一個版本，他的雇主不希望公眾知道他們使用統計測試來判斷原材料的質量。

如果我們想以置信度 p 估計母體的平均值 μ，我們需要取學生分佈 A 的 (1-p)/2 百分位數，這可以從表中查得，或者使用統計軟件（例如 Python、R 等）的內建函數計算。然後 μ 的區間可以表示為 X±A*D/√n，其中 X 是樣本的平均值，D 是標準差。

注意：我們也省略了與學生分佈相關的重要概念自由度的討論。您可以參考更完整的統計學書籍以更深入地理解這個概念。

在附帶的筆記本中提供了一個計算體重和身高置信區間的例子。

p	體重平均值
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

注意，置信概率越高，置信區間越寬。

假設檢定

在我們的棒球球員數據集中，有不同的球員角色，可以總結如下（查看附帶的筆記本以了解如何計算此表）：

角色	身高	體重	數量
捕手	72.723684	204.328947	76
指定打擊	74.222222	220.888889	18
一壘手	74.000000	213.109091	55
外野手	73.010309	199.113402	194
救援投手	74.374603	203.517460	315
二壘手	71.362069	184.344828	58
游擊手	71.903846	182.923077	52
先發投手	74.719457	205.163636	221
三壘手	73.044444	200.955556	45

我們可以注意到，一壘手的平均身高比二壘手高。因此，我們可能會得出結論：一壘手比二壘手高。

這個陳述被稱為假設，因為我們不知道這個事實是否真的成立。

然而，是否可以得出這個結論並不總是顯而易見的。從上面的討論中我們知道，每個平均值都有一個相關的置信區間，因此這種差異可能僅僅是統計誤差。我們需要更正式的方法來檢驗我們的假設。

讓我們分別計算一壘手和二壘手的身高置信區間：

置信度	一壘手	二壘手
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

我們可以看到，在任何置信度下，這些區間都不重疊。這證明了我們的假設，即一壘手比二壘手高。

更正式地說，我們正在解決的問題是檢查 兩個概率分佈是否相同，或者至少是否具有相同的參數。根據分佈的不同，我們需要使用不同的檢驗方法。如果我們知道分佈是正態分佈，我們可以應用 學生 t 檢驗。

在學生 t 檢驗中，我們計算所謂的 t 值，它表示平均值之間的差異，並考慮到方差。已證明 t 值遵循 學生分佈，這使我們能夠獲得給定置信度 p 的閾值（這可以計算或在數值表中查得）。然後我們將 t 值與該閾值進行比較，以批准或拒絕假設。

在 Python 中，我們可以使用 SciPy 套件，其中包括 ttest_ind 函數（以及許多其他有用的統計函數！）。它為我們計算 t 值，並且還反向查找置信度 p 值，因此我們只需查看置信度即可得出結論。

例如，我們比較一壘手和二壘手的身高，得到以下結果：

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

在我們的情況下，p 值非常低，這意味著有強有力的證據支持一壘手更高。

此外，我們可能希望檢驗其他類型的假設，例如：

證明某個樣本遵循某種分佈。在我們的情況下，我們假設身高是正態分佈的，但這需要正式的統計驗證。
證明樣本的平均值與某個預定值相符
比較多個樣本的平均值（例如，不同年齡組的幸福水平差異）

大數法則與中心極限定理

正態分佈如此重要的原因之一是所謂的 中心極限定理。假設我們有一個大型樣本，由獨立的 N 個值 X₁, ..., X_N 組成，這些值來自任何具有平均值 μ 和方差 σ² 的分佈。那麼，當 N 足夠大時（換句話說，當 N→∞），平均值 Σ_iX_i 將呈正態分佈，平均值為 μ，方差為 σ²/N。

中心極限定理的另一種解釋是，無論分佈如何，當您計算任何隨機變數值的和的平均值時，最終都會得到正態分佈。

根據中心極限定理，當 N→∞ 時，樣本平均值等於 μ 的概率變為 1。這被稱為 大數法則。

協方差與相關性

數據科學的一項工作是尋找數據之間的關係。我們說兩個序列相關，當它們在同一時間表現出相似的行為，即它們同時上升/下降，或者一個序列上升時另一個序列下降，反之亦然。換句話說，兩個序列之間似乎存在某種關係。

相關性並不一定表示兩個序列之間存在因果關係；有時兩個變量可能依賴於某個外部原因，或者兩個序列的相關性可能純屬偶然。然而，強數學相關性是兩個變量某種程度上相互關聯的良好指標。

數學上，顯示兩個隨機變數之間關係的主要概念是 協方差，其計算公式為：Cov(X,Y) = E[(X-E(X))(Y-E(Y))]。我們計算兩個變數偏離其平均值的偏差，然後計算這些偏差的乘積。如果兩個變數一起偏離，乘積將始終為正值，並累加為正協方差。如果兩個變數不同步偏離（即一個低於平均值而另一個高於平均值），我們將始終得到負數，並累加為負協方差。如果偏差不相關，它們將累加為大約零。

協方差的絕對值並不能告訴我們相關性有多大，因為它取決於實際值的大小。為了標準化，我們可以將協方差除以兩個變數的標準差，得到 相關性。相關性的好處是它始終在 [-1,1] 範圍內，其中 1 表示值之間的強正相關，-1 表示強負相關，0 表示完全無相關（變數是獨立的）。

例子：我們可以計算棒球球員的體重和身高之間的相關性：

print(np.corrcoef(weights,heights))

結果，我們得到如下的 相關矩陣：

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

相關矩陣 C 可以為任意數量的輸入序列 S₁, ..., S_n 計算。C_ij 的值是 S_i 和 S_j 之間的相關性，對角元素始終為 1（這也是 S_i 的自相關性）。

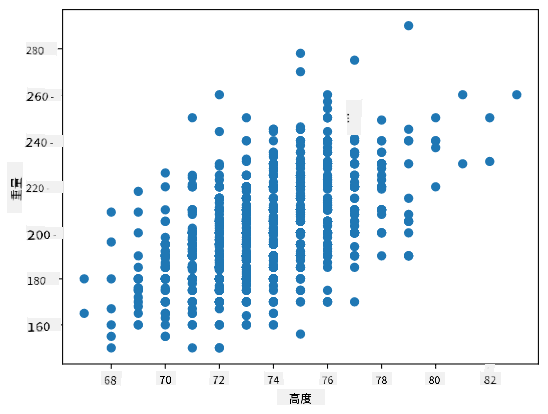
在我們的例子中，值 0.53 表明體重和身高之間存在一定的相關性。我們還可以繪製一個值對另一個值的散點圖，以直觀地查看關係：

更多相關性和協方差的例子可以在附帶的筆記本中找到。

結論

在本節中，我們學習了：

數據的基本統計屬性，例如平均值、方差、眾數和四分位數
隨機變數的不同分佈，包括正態分佈
如何找到不同屬性之間的相關性
如何使用數學和統計的嚴謹工具來證明一些假設
如何根據數據樣本計算隨機變數的置信區間

雖然這絕不是概率和統計學中所有主題的完整列表，但應該足以讓您在本課程中有一個良好的開始。

🚀 挑戰

使用筆記本中的示例代碼來測試其他假設：

一壘手比二壘手年齡更大
一壘手比三壘手更高
游擊手比二壘手更高

課後測驗

回顧與自學

概率和統計是一個非常廣泛的主題，值得開設自己的課程。如果您有興趣深入理論，可以繼續閱讀以下書籍：

Carlos Fernandez-Granda 紐約大學的講義 Probability and Statistics for Data Science（在線提供）
Peter and Andrew Bruce. Practical Statistics for Data Scientists. [R 示例代碼]。
James D. Miller. Statistics for Data Science [R 示例代碼]

作業

小型糖尿病研究

致謝

本課程由 Dmitry Soshnikov 用 ♥️ 編寫。

免責聲明：
本文件已使用 AI 翻譯服務 Co-op Translator 進行翻譯。我們致力於提供準確的翻譯，但請注意，自動翻譯可能包含錯誤或不準確之處。應以原始語言的文件作為權威來源。對於關鍵資訊，建議尋求專業人工翻譯。我們對因使用此翻譯而引起的任何誤解或錯誤解讀概不負責。

20 KiB Raw Permalink Blame History Unescape Escape