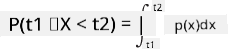25 KiB

Raw Permalink Blame History Unescape Escape

Trumpas statistikos ir tikimybių teorijos įvadas


Statistika ir tikimybių teorija - Sketchnote by @nitya

Statistika ir tikimybių teorija yra dvi glaudžiai susijusios matematikos sritys, kurios yra itin svarbios duomenų mokslui. Nors galima dirbti su duomenimis neturint gilių matematikos žinių, vis tiek verta susipažinti bent su pagrindinėmis sąvokomis. Čia pateiksime trumpą įvadą, kuris padės jums pradėti.

Prieš paskaitą: testas

Tikimybė ir atsitiktiniai kintamieji

Tikimybė yra skaičius tarp 0 ir 1, kuris parodo, kaip tikėtinas yra tam tikras įvykis. Ji apibrėžiama kaip teigiamų rezultatų (kurie veda į įvykį) skaičius, padalintas iš visų galimų rezultatų skaičiaus, jei visi rezultatai yra vienodai tikėtini. Pavyzdžiui, metant kauliuką, tikimybė gauti lyginį skaičių yra 3/6 = 0.5.

Kalbėdami apie įvykius, naudojame atsitiktinius kintamuosius. Pavyzdžiui, atsitiktinis kintamasis, kuris atspindi skaičių, gautą metant kauliuką, gali turėti reikšmes nuo 1 iki 6. Skaičių rinkinys nuo 1 iki 6 vadinamas imties erdve. Galime kalbėti apie tikimybę, kad atsitiktinis kintamasis įgaus tam tikrą reikšmę, pavyzdžiui, P(X=3)=1/6.

Ankstesniame pavyzdyje atsitiktinis kintamasis vadinamas diskrečiu, nes jo imties erdvė yra skaičiuojama, t. y. yra atskiri skaičiai, kuriuos galima išvardyti. Yra atvejų, kai imties erdvė yra realių skaičių intervalas arba visas realių skaičių rinkinys. Tokie kintamieji vadinami tęstiniais. Geras pavyzdys yra autobuso atvykimo laikas.

Tikimybių pasiskirstymas

Diskrečių atsitiktinių kintamųjų atveju lengva aprašyti kiekvieno įvykio tikimybę funkcija P(X). Kiekvienai reikšmei s iš imties erdvės S ji pateiks skaičių nuo 0 iki 1, taip, kad visų P(X=s) reikšmių suma visiems įvykiams būtų lygi 1.

Labiausiai žinomas diskretus pasiskirstymas yra vienodas pasiskirstymas, kai imties erdvėje yra N elementų, kurių kiekvieno tikimybė yra 1/N.

Tęstinių kintamųjų pasiskirstymą aprašyti yra sudėtingiau, kai reikšmės imamos iš tam tikro intervalo [a,b] arba viso realių skaičių rinkinio ℝ. Pavyzdžiui, autobuso atvykimo laikas. Iš tiesų, tikimybė, kad autobusas atvyks tiksliai tam tikru laiku t, yra lygi 0!

Dabar žinote, kad įvykiai, kurių tikimybė yra 0, vis tiek įvyksta, ir gana dažnai! Bent jau kiekvieną kartą, kai atvyksta autobusas!

Galime kalbėti tik apie tikimybę, kad kintamasis pateks į tam tikrą reikšmių intervalą, pvz., P(t₁≤X<t₂). Tokiu atveju tikimybių pasiskirstymas aprašomas tikimybių tankio funkcija p(x), tokia, kad

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Tęstinis vienodo pasiskirstymo analogas vadinamas tęstiniu vienodu pasiskirstymu, kuris apibrėžiamas baigtiniame intervale. Tikimybė, kad reikšmė X pateks į intervalo ilgį l, yra proporcinga l ir didėja iki 1.

Kitas svarbus pasiskirstymas yra normalusis pasiskirstymas, apie kurį plačiau kalbėsime toliau.

Vidurkis, dispersija ir standartinis nuokrypis

Tarkime, kad paimame n atsitiktinio kintamojo X imčių seką: x₁, x₂, ..., x_n. Galime apibrėžti vidurkį (arba aritmetinį vidurkį) tradiciniu būdu kaip (x₁+x₂+x_n)/n. Didinant imties dydį (t. y. imant ribą su n→∞), gausime pasiskirstymo vidurkį (dar vadinamą lūkesčiu). Lūkesčius žymėsime E(x).

Galima parodyti, kad bet kuriam diskrečiam pasiskirstymui su reikšmėmis {x₁, x₂, ..., x_N} ir atitinkamomis tikimybėmis p₁, p₂, ..., p_N, lūkesčiai bus lygūs E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Norėdami nustatyti, kaip plačiai paskirstytos reikšmės, galime apskaičiuoti dispersiją σ² = ∑(x_i - μ)²/n, kur μ yra sekos vidurkis. Reikšmė σ vadinama standartiniu nuokrypiu, o σ² vadinama dispersija.

Moda, mediana ir kvartiliai

Kartais vidurkis nepakankamai gerai atspindi „tipinę“ duomenų reikšmę. Pavyzdžiui, kai yra keletas ekstremalių reikšmių, kurios visiškai neatitinka diapazono, jos gali paveikti vidurkį. Kitas geras rodiklis yra mediana, reikšmė, tokia, kad pusė duomenų taškų yra mažesni už ją, o kita pusė - didesni.

Norėdami geriau suprasti duomenų pasiskirstymą, naudinga kalbėti apie kvartilius:

Pirmasis kvartilis, arba Q1, yra reikšmė, tokia, kad 25% duomenų yra mažesni už ją
Trečiasis kvartilis, arba Q3, yra reikšmė, tokia, kad 75% duomenų yra mažesni už ją

Grafiškai galime pavaizduoti medianos ir kvartilių santykį diagramoje, vadinamoje dėžės diagrama:

Čia taip pat apskaičiuojame tarpkvartilinį diapazoną IQR=Q3-Q1 ir vadinamuosius išskirtinius taškus - reikšmes, kurios yra už ribų [Q1-1.5IQR,Q3+1.5IQR].

Mažos galimų reikšmių skaičiaus baigtiniame pasiskirstyme geras „tipinis“ rodiklis yra dažniausiai pasikartojanti reikšmė, vadinama moda. Ji dažnai taikoma kategoriniams duomenims, tokiems kaip spalvos. Įsivaizduokite situaciją, kai turime dvi žmonių grupes - vieni stipriai mėgsta raudoną spalvą, o kiti - mėlyną. Jei spalvas koduotume skaičiais, vidutinė mėgstamos spalvos reikšmė būtų kažkur oranžinės-žalios spektro ribose, kas neatspindėtų nei vienos grupės tikrosios preferencijos. Tačiau moda būtų viena iš spalvų arba abi spalvos, jei žmonių, balsuojančių už jas, skaičius būtų vienodas (tokiu atveju imtis vadinama daugiamodine).

Realūs duomenys

Analizuojant realaus pasaulio duomenis, jie dažnai nėra tikri atsitiktiniai kintamieji, ta prasme, kad neatliekame eksperimentų su nežinomu rezultatu. Pavyzdžiui, apsvarstykime beisbolo žaidėjų komandą ir jų kūno duomenis, tokius kaip ūgis, svoris ir amžius. Šie skaičiai nėra visiškai atsitiktiniai, tačiau vis tiek galime taikyti tuos pačius matematinius konceptus. Pavyzdžiui, žmonių svorių seka gali būti laikoma reikšmių seka, paimta iš tam tikro atsitiktinio kintamojo. Žemiau pateikiama faktinių beisbolo žaidėjų svorių seka iš Major League Baseball, paimta iš šio duomenų rinkinio (patogumui pateikiamos tik pirmos 20 reikšmių):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Note: Norėdami pamatyti, kaip dirbti su šiuo duomenų rinkiniu, peržiūrėkite pridedamą užrašų knygelę. Pamokoje yra keletas užduočių, kurias galite atlikti pridėdami kodą į tą užrašų knygelę. Jei nesate tikri, kaip dirbti su duomenimis, nesijaudinkite - vėliau grįšime prie darbo su duomenimis naudojant Python. Jei nežinote, kaip vykdyti kodą Jupyter Notebook, peržiūrėkite šį straipsnį.

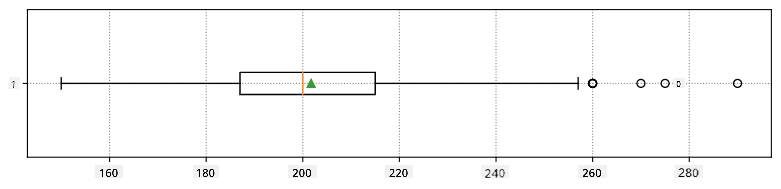
Štai dėžės diagrama, rodanti vidurkį, medianą ir kvartilius mūsų duomenims:

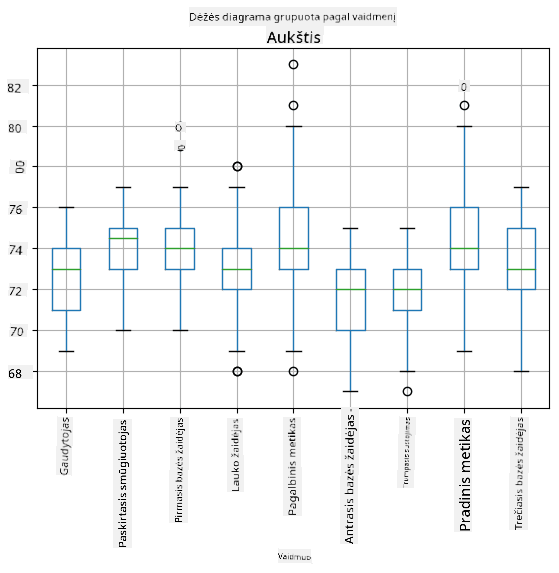
Kadangi mūsų duomenyse yra informacija apie skirtingus žaidėjų vaidmenis, galime sudaryti dėžės diagramą pagal vaidmenį - tai leis mums suprasti, kaip parametrų reikšmės skiriasi tarp vaidmenų. Šį kartą apsvarstysime ūgį:

Ši diagrama rodo, kad, vidutiniškai, pirmosios bazės žaidėjų ūgis yra didesnis nei antrosios bazės žaidėjų ūgis. Vėliau šioje pamokoje išmoksime, kaip formaliau patikrinti šią hipotezę ir kaip parodyti, kad mūsų duomenys yra statistiškai reikšmingi tai įrodyti.

Dirbdami su realaus pasaulio duomenimis, darome prielaidą, kad visi duomenų taškai yra imtys, paimtos iš tam tikro tikimybių pasiskirstymo. Ši prielaida leidžia taikyti mašininio mokymosi metodus ir kurti veikiančius prognozavimo modelius.

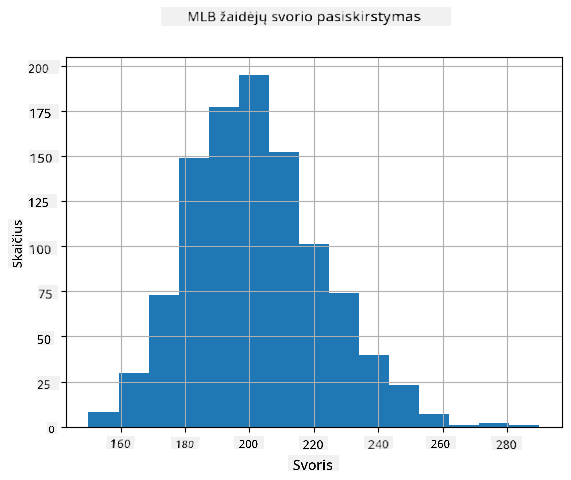
Norėdami pamatyti, koks yra mūsų duomenų pasiskirstymas, galime sudaryti grafiką, vadinamą histograma. X ašis turėtų turėti skirtingų svorio intervalų skaičių (vadinamų dėžėmis), o vertikali ašis rodytų, kiek kartų mūsų atsitiktinio kintamojo imtis pateko į tam tikrą intervalą.

Iš šios histogramos matote, kad visos reikšmės yra sutelktos aplink tam tikrą vidutinį svorį, o kuo toliau nuo to svorio - tuo mažiau svorių su ta reikšme yra aptinkama. T. y., labai mažai tikėtina, kad beisbolo žaidėjo svoris labai skirsis nuo vidutinio svorio. Svorio dispersija rodo, kiek svoriai gali skirtis nuo vidurkio.

Jei paimtume kitų žmonių, ne iš beisbolo lygos, svorius, pasiskirstymas greičiausiai būtų kitoks. Tačiau pasiskirstymo forma išliktų ta pati, tik vidurkis ir dispersija pasikeistų. Taigi, jei treniruosime savo modelį su beisbolo žaidėjais, jis greičiausiai pateiks neteisingus rezultatus, kai bus taikomas universiteto studentams, nes pagrindinis pasiskirstymas yra kitoks.

Normalusis pasiskirstymas

Svorio pasiskirstymas, kurį matėme aukščiau, yra labai tipiškas, ir daugelis realaus pasaulio matavimų seka tokio tipo pasiskirstymą, tačiau su skirtingu vidurkiu ir dispersija. Šis pasiskirstymas vadinamas normaliuoju pasiskirstymu, ir jis vaidina labai svarbų vaidmenį statistikoje.

Naudoti normalųjį pasiskirstymą yra teisingas būdas generuoti potencialių beisbolo žaidėjų atsitiktinius svorius. Kai žinome vidutinį svorį mean ir standartinį nuokrypį std, galime sugeneruoti 1000 svorio imčių šiuo būdu:

samples = np.random.normal(mean,std,1000)

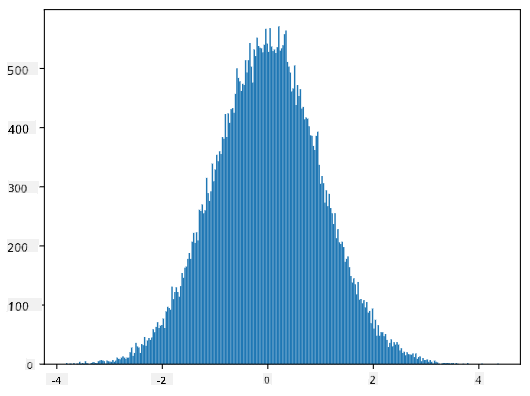
Jei sudarysime sugeneruotų imčių histogramą, pamatysime vaizdą, labai panašų į aukščiau pateiktą. O jei padidinsime imčių skaičių ir dėžių skaičių, galime sugeneruoti normalaus pasiskirstymo vaizdą, kuris bus artimesnis idealiam:

Normalusis pasiskirstymas su vidurkiu=0 ir standartiniu nuokrypiu=1

Pasitikėjimo intervalai

Kalbėdami apie beisbolo žaidėjų svorius, darome prielaidą, kad yra tam tikras atsitiktinis kintamasis W, kuris atitinka idealų visų beisbolo žaidėjų svorių tikimybių pasiskirstymą (vadinamą populiacija). Mūsų svorių seka atitinka visų beisbolo žaidėjų pogrupį, kurį vadiname imčiu. Įdomus klausimas yra, ar galime žinoti W pasiskirstymo parametrus, t. y. populiacijos vidurkį ir dispersiją?

Lengviausias atsakymas būtų apskaičiuoti mūsų imties vidurkį ir dispersiją. Tačiau gali nutikti taip, kad mūsų atsitiktinė imtis netiksliai atspindi visą populiaciją. Todėl prasminga kalbėti apie pasitikėjimo intervalą.

Pasitikėjimo intervalas yra tikrosios populiacijos vidurkio įvertinimas, remiantis mūsų imtimi, kuris yra tikslus tam tikra tikimybe (arba pasitikėjimo lygiu). Tarkime, turime imtį X₁, ..., X_n iš mūsų skirstinio. Kiekvieną kartą imdami imtį iš skirstinio, gausime skirtingą vidurkio reikšmę μ. Todėl μ galima laikyti atsitiktiniu dydžiu. Pasitikėjimo intervalas su pasitikėjimu p yra reikšmių pora (L_p, R_p), tokia, kad P(L_p≤μ≤R_p) = p, t. y. tikimybė, kad išmatuotas vidurkis pateks į intervalą, yra lygi p.

Išsamiai aptarti, kaip skaičiuojami šie pasitikėjimo intervalai, peržengia mūsų trumpo įvado ribas. Daugiau informacijos galite rasti Vikipedijoje. Trumpai tariant, mes apibrėžiame apskaičiuoto imties vidurkio skirstinį, palyginti su tikruoju populiacijos vidurkiu, kuris vadinamas studento skirstiniu.

Įdomus faktas: Studento skirstinys pavadintas matematiko William Sealy Gosset vardu, kuris savo darbą paskelbė pseudonimu „Student“. Jis dirbo Guinness alaus darykloje, ir, pasak vienos versijos, jo darbdavys nenorėjo, kad visuomenė sužinotų, jog jie naudoja statistinius testus žaliavų kokybei nustatyti.

Jei norime įvertinti populiacijos vidurkį μ su pasitikėjimu p, turime paimti (1-p)/2-tąjį procentilį iš Studento skirstinio A, kurį galima rasti lentelėse arba apskaičiuoti naudojant statistinės programinės įrangos (pvz., Python, R ir kt.) funkcijas. Tada intervalas μ būtų X±A*D/√n, kur X yra gautas imties vidurkis, o D – standartinis nuokrypis.

Pastaba: Taip pat praleidžiame svarbios sąvokos – laisvės laipsnių – aptarimą, kuri yra svarbi Studento skirstinio kontekste. Norėdami giliau suprasti šią sąvoką, galite kreiptis į išsamesnes statistikos knygas.

Pavyzdys, kaip apskaičiuoti pasitikėjimo intervalą svoriams ir ūgiams, pateiktas pridedamuose užrašų knygelėse.

p	Svorio vidurkis
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Atkreipkite dėmesį, kad kuo didesnė pasitikėjimo tikimybė, tuo platesnis pasitikėjimo intervalas.

Hipotezių tikrinimas

Mūsų beisbolo žaidėjų duomenų rinkinyje yra skirtingi žaidėjų vaidmenys, kurie gali būti apibendrinti taip (pažiūrėkite į pridedamą užrašų knygelę, kad pamatytumėte, kaip ši lentelė apskaičiuojama):

Vaidmuo	Ūgis	Svoris	Kiekis
Gaudytojas	72.723684	204.328947	76
Smūgiuotojas	74.222222	220.888889	18
Pirmasis bazininkas	74.000000	213.109091	55
Lauko žaidėjas	73.010309	199.113402	194
Atsarginis metikas	74.374603	203.517460	315
Antrasis bazininkas	71.362069	184.344828	58
Trumpasis žaidėjas	71.903846	182.923077	52
Pagrindinis metikas	74.719457	205.163636	221
Trečiasis bazininkas	73.044444	200.955556	45

Galime pastebėti, kad pirmųjų bazininkų vidutinis ūgis yra didesnis nei antrųjų bazininkų. Todėl galime būti linkę daryti išvadą, kad pirmieji bazininkai yra aukštesni nei antrieji bazininkai.

Šis teiginys vadinamas hipoteze, nes mes nežinome, ar tai iš tikrųjų tiesa.

Tačiau ne visada akivaizdu, ar galime padaryti tokią išvadą. Iš aukščiau pateiktos diskusijos žinome, kad kiekvienas vidurkis turi susijusį pasitikėjimo intervalą, todėl šis skirtumas gali būti tik statistinė paklaida. Mums reikia formalesnio būdo hipotezei patikrinti.

Apskaičiuokime pasitikėjimo intervalus atskirai pirmųjų ir antrųjų bazininkų ūgiams:

Pasitikėjimas	Pirmieji bazininkai	Antrieji bazininkai
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Matome, kad nė vienu pasitikėjimo lygiu intervalai nesutampa. Tai įrodo mūsų hipotezę, kad pirmieji bazininkai yra aukštesni nei antrieji bazininkai.

Formaliau, problema, kurią sprendžiame, yra nustatyti, ar du skirstiniai yra vienodi, ar bent jau turi tuos pačius parametrus. Priklausomai nuo skirstinio, tam reikia naudoti skirtingus testus. Jei žinome, kad mūsų skirstiniai yra normalūs, galime taikyti Studento t-testą.

Studento t-teste apskaičiuojame vadinamąją t-reikšmę, kuri nurodo vidurkių skirtumą, atsižvelgiant į dispersiją. Įrodyta, kad t-reikšmė atitinka studento skirstinį, kuris leidžia mums gauti ribinę reikšmę tam tikram pasitikėjimo lygiui p (tai galima apskaičiuoti arba rasti skaitmeninėse lentelėse). Tada lyginame t-reikšmę su šia riba, kad patvirtintume arba paneigtume hipotezę.

Python kalboje galime naudoti SciPy biblioteką, kurioje yra funkcija ttest_ind (be daugelio kitų naudingų statistinių funkcijų!). Ji apskaičiuoja t-reikšmę už mus ir taip pat atlieka atvirkštinį pasitikėjimo p-reikšmės nustatymą, kad galėtume tiesiog pažvelgti į pasitikėjimą ir padaryti išvadą.

Pavyzdžiui, mūsų pirmųjų ir antrųjų bazininkų ūgių palyginimas duoda šiuos rezultatus:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

Mūsų atveju p-reikšmė yra labai maža, o tai reiškia, kad yra stiprūs įrodymai, patvirtinantys, jog pirmieji bazininkai yra aukštesni.

Taip pat yra kitų hipotezių tipų, kuriuos galime norėti patikrinti, pavyzdžiui:

Įrodyti, kad tam tikra imtis atitinka tam tikrą skirstinį. Mūsų atveju mes darėme prielaidą, kad ūgiai yra normaliai pasiskirstę, tačiau tai reikia formaliai statistiškai patvirtinti.
Įrodyti, kad imties vidurkis atitinka tam tikrą iš anksto nustatytą reikšmę.
Palyginti kelių imčių vidurkius (pvz., koks yra laimės lygio skirtumas tarp skirtingų amžiaus grupių).

Didelių skaičių dėsnis ir centrinė ribinė teorema

Viena iš priežasčių, kodėl normalusis skirstinys yra toks svarbus, yra vadinamoji centrinė ribinė teorema. Tarkime, turime didelę nepriklausomų N reikšmių X₁, ..., X_N imtį, paimtą iš bet kokio skirstinio su vidurkiu μ ir dispersija σ². Tada, kai N yra pakankamai didelis (kitaip tariant, kai N→∞), vidurkis Σ_iX_i bus normaliai pasiskirstęs, su vidurkiu μ ir dispersija σ²/N.

Kitas būdas interpretuoti centrinę ribinę teoremą yra sakyti, kad nepriklausomai nuo skirstinio, kai apskaičiuojate bet kokių atsitiktinių dydžių sumos vidurkį, gaunate normalųjį skirstinį.

Iš centrinės ribinės teoremos taip pat seka, kad kai N→∞, tikimybė, jog imties vidurkis bus lygus μ, tampa 1. Tai vadinama didelių skaičių dėsniu.

Kovariacija ir koreliacija

Viena iš duomenų mokslo užduočių yra rasti ryšius tarp duomenų. Sakome, kad dvi sekos koreliuoja, kai jos elgiasi panašiai tuo pačiu metu, t. y. jos arba kyla/krenta kartu, arba viena seka kyla, kai kita krenta, ir atvirkščiai. Kitaip tariant, tarp dviejų sekų atrodo esąs tam tikras ryšys.

Koreliacija nebūtinai reiškia priežastinį ryšį tarp dviejų sekų; kartais abu kintamieji gali priklausyti nuo kokios nors išorinės priežasties arba gali būti grynas atsitiktinumas, kad dvi sekos koreliuoja. Tačiau stipri matematinė koreliacija yra geras rodiklis, kad du kintamieji yra kažkaip susiję.

Matematiškai pagrindinė sąvoka, rodanti ryšį tarp dviejų atsitiktinių dydžių, yra kovariacija, kuri apskaičiuojama taip: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Mes apskaičiuojame abiejų kintamųjų nuokrypį nuo jų vidurkių ir tada šių nuokrypių sandaugą. Jei abu kintamieji nukrypsta kartu, sandauga visada bus teigiama, o tai sudarys teigiamą kovariaciją. Jei abu kintamieji nukrypsta nesinchroniškai (t. y. vienas nukrenta žemiau vidurkio, kai kitas pakyla aukščiau vidurkio), visada gausime neigiamas reikšmes, kurios sudarys neigiamą kovariaciją. Jei nuokrypiai nėra priklausomi, jie sudarys apytiksliai nulį.

Kovariacijos absoliuti reikšmė nepasako daug apie tai, kokia stipri yra koreliacija, nes ji priklauso nuo faktinių reikšmių dydžio. Norėdami ją normalizuoti, galime padalyti kovariaciją iš abiejų kintamųjų standartinio nuokrypio ir gauti koreliaciją. Gerai tai, kad koreliacija visada yra intervale [-1,1], kur 1 reiškia stiprią teigiamą koreliaciją tarp reikšmių, -1 – stiprią neigiamą koreliaciją, o 0 – jokios koreliacijos (kintamieji yra nepriklausomi).

Pavyzdys: Galime apskaičiuoti koreliaciją tarp beisbolo žaidėjų svorių ir ūgių iš aukščiau paminėto duomenų rinkinio:

print(np.corrcoef(weights,heights))

Rezultate gauname koreliacijos matricą, panašią į šią:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Koreliacijos matrica C gali būti apskaičiuota bet kokiam įvesties sekų S₁, ..., S_n skaičiui. C_ij reikšmė yra koreliacija tarp S_i ir S_j, o įstrižainės elementai visada yra 1 (tai taip pat yra S_i savikoreliacija).

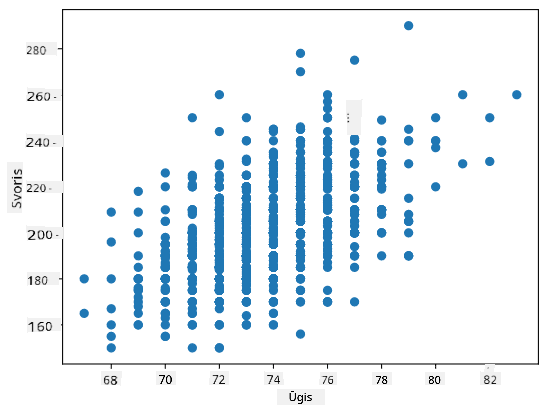
Mūsų atveju reikšmė 0.53 rodo, kad yra tam tikra koreliacija tarp žmogaus svorio ir ūgio. Taip pat galime sudaryti sklaidos diagramą, kurioje viena reikšmė vaizduojama prieš kitą, kad vizualiai pamatytume ryšį:

Daugiau koreliacijos ir kovariacijos pavyzdžių galite rasti pridedamoje užrašų knygelėje.

Išvada

Šioje dalyje išmokome:

pagrindines duomenų statistines savybes, tokias kaip vidurkis, dispersija, moda ir kvartiliai
skirtingus atsitiktinių dydžių skirstinius, įskaitant normalųjį skirstinį
kaip rasti koreliaciją tarp skirtingų savybių
kaip naudoti matematikos ir statistikos metodus hipotezėms įrodyti
kaip apskaičiuoti atsitiktinio dydžio pasitikėjimo intervalus, remiantis duomenų imtimi

Nors tai tikrai nėra išsamus tikimybių ir statistikos temų sąrašas, jis turėtų būti pakankamas, kad suteiktų jums gerą pradžią šiame kurse.

🚀 Iššūkis

Naudokite užrašų knygelėje pateiktą pavyzdinį kodą, kad patikrintumėte kitas hipotezes:

Pirmieji bazininkai yra vyresni nei antrieji bazininkai
Pirmieji bazininkai yra aukštesni nei tretieji bazininkai
Trumpieji žaidėjai yra aukštesni nei antrieji bazininkai

Po paskaitos testas

Peržiūra ir savarankiškas mokymasis

Tikimybė ir statistika yra tokia plati tema, kad ji nusipelno atskiro kurso. Jei norite giliau pasinerti į teoriją, galite toliau skaityti šias knygas:

Carlos Fernandez-Granda iš Niujorko universiteto turi puikius paskaitų užrašus Probability and Statistics for Data Science (prieinami internete)
Peter ir Andrew Bruce. Practical Statistics for Data Scientists. [pavyzdinis kodas R].
James D. Miller. Statistics for Data Science [pavyzdinis kodas R]

Užduotis

Mažas diabeto tyrimas

Kreditas

Šią pamoką su ♥️ parengė Dmitry Soshnikov

Atsakomybės apribojimas:
Šis dokumentas buvo išverstas naudojant dirbtinio intelekto vertimo paslaugą Co-op Translator. Nors siekiame tikslumo, atkreipiame dėmesį, kad automatiniai vertimai gali turėti klaidų ar netikslumų. Originalus dokumentas jo gimtąja kalba turėtų būti laikomas autoritetingu šaltiniu. Kritinei informacijai rekomenduojama naudoti profesionalų žmogaus vertimą. Mes neprisiimame atsakomybės už nesusipratimus ar klaidingus aiškinimus, kylančius dėl šio vertimo naudojimo.

25 KiB Raw Permalink Blame History Unescape Escape