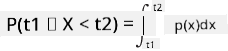25 KiB

Raw Permalink Blame History Unescape Escape

Pengantar Singkat tentang Statistik dan Probabilitas


Statistik dan Probabilitas - Sketchnote oleh @nitya

Teori Statistik dan Probabilitas adalah dua cabang Matematika yang sangat berkaitan dan sangat relevan dengan Ilmu Data. Meskipun memungkinkan untuk bekerja dengan data tanpa pengetahuan matematika yang mendalam, tetap lebih baik untuk memahami setidaknya beberapa konsep dasar. Di sini, kami akan memberikan pengantar singkat yang akan membantu Anda memulai.

Kuis Pra-Kuliah

Probabilitas dan Variabel Acak

Probabilitas adalah angka antara 0 dan 1 yang menyatakan seberapa mungkin suatu kejadian terjadi. Probabilitas didefinisikan sebagai jumlah hasil positif (yang mengarah pada kejadian tersebut), dibagi dengan jumlah total hasil, dengan asumsi semua hasil memiliki kemungkinan yang sama. Sebagai contoh, ketika kita melempar dadu, probabilitas mendapatkan angka genap adalah 3/6 = 0,5.

Ketika kita berbicara tentang kejadian, kita menggunakan variabel acak. Sebagai contoh, variabel acak yang mewakili angka yang diperoleh saat melempar dadu akan memiliki nilai dari 1 hingga 6. Kumpulan angka dari 1 hingga 6 disebut ruang sampel. Kita dapat berbicara tentang probabilitas variabel acak mengambil nilai tertentu, misalnya P(X=3)=1/6.

Variabel acak dalam contoh sebelumnya disebut diskrit, karena memiliki ruang sampel yang dapat dihitung, yaitu terdapat nilai-nilai terpisah yang dapat dijumlahkan. Ada kasus di mana ruang sampel adalah rentang bilangan real, atau seluruh himpunan bilangan real. Variabel seperti ini disebut kontinu. Contoh yang baik adalah waktu kedatangan bus.

Distribusi Probabilitas

Dalam kasus variabel acak diskrit, mudah untuk menggambarkan probabilitas setiap kejadian dengan fungsi P(X). Untuk setiap nilai s dari ruang sampel S, fungsi ini akan memberikan angka antara 0 dan 1, sehingga jumlah semua nilai P(X=s) untuk semua kejadian adalah 1.

Distribusi diskrit yang paling dikenal adalah distribusi uniform, di mana terdapat ruang sampel dengan N elemen, dengan probabilitas yang sama sebesar 1/N untuk masing-masing elemen.

Lebih sulit untuk menggambarkan distribusi probabilitas variabel kontinu, dengan nilai-nilai yang diambil dari interval [a,b], atau seluruh himpunan bilangan real ℝ. Pertimbangkan kasus waktu kedatangan bus. Faktanya, untuk setiap waktu kedatangan t yang tepat, probabilitas bus tiba tepat pada waktu tersebut adalah 0!

Sekarang Anda tahu bahwa kejadian dengan probabilitas 0 bisa terjadi, dan sering kali terjadi! Setidaknya setiap kali bus tiba!

Kita hanya dapat berbicara tentang probabilitas variabel jatuh dalam interval nilai tertentu, misalnya P(t₁≤X<t₂). Dalam kasus ini, distribusi probabilitas dijelaskan oleh fungsi kepadatan probabilitas p(x), sehingga

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Analog kontinu dari distribusi uniform disebut uniform kontinu, yang didefinisikan pada interval terbatas. Probabilitas bahwa nilai X jatuh ke dalam interval dengan panjang l sebanding dengan l, dan meningkat hingga 1.

Distribusi penting lainnya adalah distribusi normal, yang akan kita bahas lebih detail di bawah.

Rata-rata, Variansi, dan Simpangan Baku

Misalkan kita mengambil urutan n sampel dari variabel acak X: x₁, x₂, ..., x_n. Kita dapat mendefinisikan nilai rata-rata (atau rata-rata aritmatika) dari urutan tersebut dengan cara tradisional sebagai (x₁+x₂+x_n)/n. Ketika ukuran sampel bertambah besar (yaitu mengambil limit dengan n→∞), kita akan mendapatkan rata-rata (juga disebut ekspektasi) dari distribusi. Kita akan menyebut ekspektasi ini sebagai E(x).

Dapat ditunjukkan bahwa untuk distribusi diskrit apa pun dengan nilai {x₁, x₂, ..., x_N} dan probabilitas yang sesuai p₁, p₂, ..., p_N, ekspektasi akan sama dengan E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Untuk mengidentifikasi seberapa jauh nilai-nilai tersebar, kita dapat menghitung variansi σ² = ∑(x_i - μ)²/n, di mana μ adalah rata-rata dari urutan tersebut. Nilai σ disebut simpangan baku, dan σ² disebut variansi.

Modus, Median, dan Kuartil

Kadang-kadang, rata-rata tidak cukup mewakili nilai "tipikal" untuk data. Misalnya, ketika ada beberapa nilai ekstrem yang benar-benar di luar jangkauan, nilai-nilai tersebut dapat memengaruhi rata-rata. Indikator lain yang baik adalah median, yaitu nilai di mana separuh data berada di bawahnya, dan separuh lainnya di atasnya.

Untuk membantu kita memahami distribusi data, berguna untuk berbicara tentang kuartil:

Kuartil pertama, atau Q1, adalah nilai di mana 25% data berada di bawahnya
Kuartil ketiga, atau Q3, adalah nilai di mana 75% data berada di bawahnya

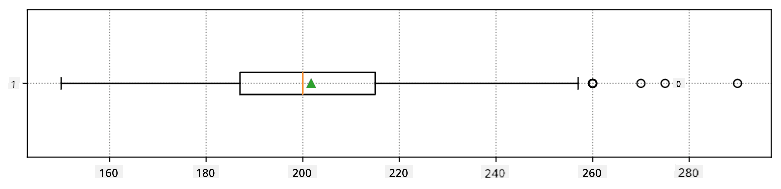
Secara grafis, kita dapat merepresentasikan hubungan antara median dan kuartil dalam diagram yang disebut box plot:

Di sini kita juga menghitung rentang antar-kuartil IQR=Q3-Q1, dan yang disebut outlier - nilai-nilai yang berada di luar batas [Q1-1.5IQR,Q3+1.5IQR].

Untuk distribusi terbatas yang mengandung sejumlah kecil nilai yang mungkin, nilai "tipikal" yang baik adalah nilai yang paling sering muncul, yang disebut modus. Modus sering diterapkan pada data kategorikal, seperti warna. Pertimbangkan situasi di mana kita memiliki dua kelompok orang - beberapa sangat menyukai warna merah, dan lainnya menyukai warna biru. Jika kita mengkodekan warna dengan angka, nilai rata-rata untuk warna favorit akan berada di spektrum oranye-hijau, yang tidak menunjukkan preferensi sebenarnya dari kedua kelompok. Namun, modus akan menjadi salah satu warna, atau kedua warna, jika jumlah orang yang memilihnya sama (dalam kasus ini kita menyebut sampel tersebut multimodal).

Data Dunia Nyata

Ketika kita menganalisis data dari dunia nyata, data tersebut sering kali bukan variabel acak dalam arti bahwa kita tidak melakukan eksperimen dengan hasil yang tidak diketahui. Sebagai contoh, pertimbangkan tim pemain bisbol, dan data tubuh mereka, seperti tinggi, berat, dan usia. Angka-angka tersebut tidak sepenuhnya acak, tetapi kita masih dapat menerapkan konsep matematika yang sama. Sebagai contoh, urutan berat badan orang dapat dianggap sebagai urutan nilai yang diambil dari suatu variabel acak. Di bawah ini adalah urutan berat badan pemain bisbol sebenarnya dari Major League Baseball, diambil dari dataset ini (untuk kenyamanan Anda, hanya 20 nilai pertama yang ditampilkan):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Catatan: Untuk melihat contoh bekerja dengan dataset ini, lihat notebook yang menyertainya. Ada juga sejumlah tantangan sepanjang pelajaran ini, dan Anda dapat menyelesaikannya dengan menambahkan beberapa kode ke notebook tersebut. Jika Anda tidak yakin bagaimana mengoperasikan data, jangan khawatir - kita akan kembali ke cara bekerja dengan data menggunakan Python di waktu mendatang. Jika Anda tidak tahu cara menjalankan kode di Jupyter Notebook, lihat artikel ini.

Berikut adalah box plot yang menunjukkan rata-rata, median, dan kuartil untuk data kita:

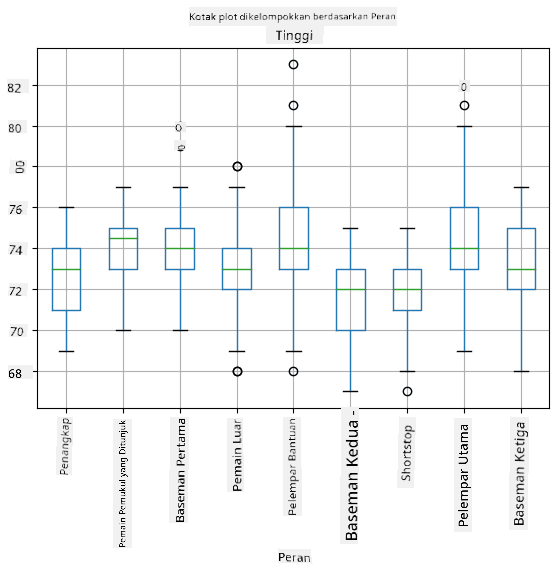
Karena data kita mengandung informasi tentang peran pemain yang berbeda, kita juga dapat membuat box plot berdasarkan peran - ini akan memungkinkan kita untuk mendapatkan gambaran tentang bagaimana nilai parameter berbeda di antara peran. Kali ini kita akan mempertimbangkan tinggi badan:

Diagram ini menunjukkan bahwa, rata-rata, tinggi pemain basemen pertama lebih tinggi daripada pemain basemen kedua. Nanti dalam pelajaran ini kita akan belajar bagaimana kita dapat menguji hipotesis ini secara lebih formal, dan bagaimana menunjukkan bahwa data kita secara statistik signifikan untuk mendukung hal tersebut.

Ketika bekerja dengan data dunia nyata, kita mengasumsikan bahwa semua titik data adalah sampel yang diambil dari suatu distribusi probabilitas. Asumsi ini memungkinkan kita untuk menerapkan teknik pembelajaran mesin dan membangun model prediktif yang berfungsi.

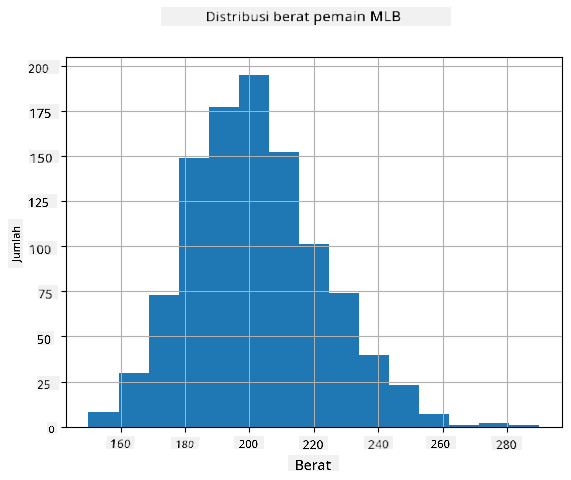
Untuk melihat distribusi data kita, kita dapat membuat grafik yang disebut histogram. Sumbu X akan berisi sejumlah interval berat yang berbeda (disebut bin), dan sumbu vertikal akan menunjukkan jumlah sampel variabel acak kita yang berada dalam interval tertentu.

Dari histogram ini, Anda dapat melihat bahwa semua nilai terpusat di sekitar berat rata-rata tertentu, dan semakin jauh kita dari berat tersebut - semakin sedikit berat dengan nilai tersebut yang ditemukan. Artinya, sangat tidak mungkin bahwa berat pemain bisbol akan sangat berbeda dari berat rata-rata. Variansi berat menunjukkan sejauh mana berat cenderung berbeda dari rata-rata.

Jika kita mengambil berat orang lain, bukan dari liga bisbol, distribusinya kemungkinan akan berbeda. Namun, bentuk distribusinya akan sama, tetapi rata-rata dan variansinya akan berubah. Jadi, jika kita melatih model kita pada pemain bisbol, kemungkinan besar model tersebut akan memberikan hasil yang salah ketika diterapkan pada mahasiswa universitas, karena distribusi dasarnya berbeda.

Distribusi Normal

Distribusi berat yang kita lihat di atas sangat khas, dan banyak pengukuran dari dunia nyata mengikuti jenis distribusi yang sama, tetapi dengan rata-rata dan variansi yang berbeda. Distribusi ini disebut distribusi normal, dan memainkan peran yang sangat penting dalam statistik.

Menggunakan distribusi normal adalah cara yang benar untuk menghasilkan berat acak dari calon pemain bisbol. Setelah kita mengetahui berat rata-rata mean dan simpangan baku std, kita dapat menghasilkan 1000 sampel berat dengan cara berikut:

samples = np.random.normal(mean,std,1000)

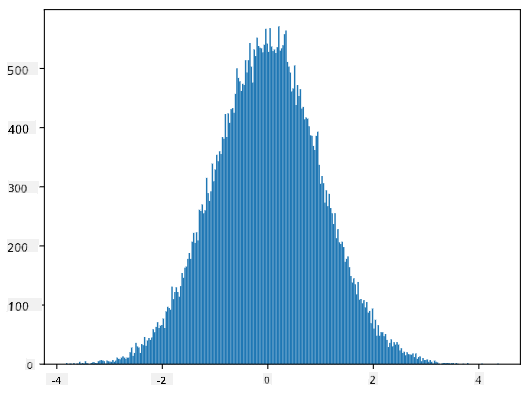
Jika kita membuat histogram dari sampel yang dihasilkan, kita akan melihat gambar yang sangat mirip dengan yang ditunjukkan di atas. Dan jika kita meningkatkan jumlah sampel dan jumlah bin, kita dapat menghasilkan gambar distribusi normal yang lebih mendekati ideal:

Distribusi Normal dengan mean=0 dan std.dev=1

Interval Kepercayaan

Ketika kita berbicara tentang berat pemain bisbol, kita mengasumsikan bahwa ada variabel acak W tertentu yang sesuai dengan distribusi probabilitas ideal dari berat semua pemain bisbol (yang disebut populasi). Urutan berat kita sesuai dengan subset dari semua pemain bisbol yang kita sebut sampel. Pertanyaan menarik adalah, bisakah kita mengetahui parameter distribusi W, yaitu rata-rata dan variansi populasi?

Jawaban termudah adalah menghitung rata-rata dan variansi dari sampel kita. Namun, bisa saja sampel acak kita tidak secara akurat mewakili populasi lengkap. Oleh karena itu, masuk akal untuk berbicara tentang interval kepercayaan.

Interval kepercayaan adalah estimasi rata-rata sebenarnya dari populasi berdasarkan sampel kita, yang akurat dengan probabilitas tertentu (atau tingkat kepercayaan). Misalkan kita memiliki sampel X₁, ..., X_n dari distribusi kita. Setiap kali kita mengambil sampel dari distribusi tersebut, kita akan mendapatkan nilai rata-rata μ yang berbeda. Oleh karena itu, μ dapat dianggap sebagai variabel acak. Interval kepercayaan dengan tingkat kepercayaan p adalah sepasang nilai (L_p, R_p), sehingga P(L_p≤μ≤R_p) = p, yaitu probabilitas nilai rata-rata yang diukur berada dalam interval tersebut sama dengan p.

Pembahasan rinci tentang bagaimana interval kepercayaan ini dihitung melampaui pengantar singkat ini. Beberapa detail lebih lanjut dapat ditemukan di Wikipedia. Secara singkat, kita mendefinisikan distribusi rata-rata sampel yang dihitung relatif terhadap rata-rata sebenarnya dari populasi, yang disebut distribusi student.

Fakta menarik: Distribusi student dinamai dari matematikawan William Sealy Gosset, yang menerbitkan makalahnya dengan nama pena "Student". Ia bekerja di pabrik bir Guinness, dan, menurut salah satu versi, majikannya tidak ingin publik mengetahui bahwa mereka menggunakan uji statistik untuk menentukan kualitas bahan baku.

Jika kita ingin memperkirakan rata-rata μ dari populasi kita dengan tingkat kepercayaan p, kita perlu mengambil persentil (1-p)/2 dari distribusi student A, yang dapat diambil dari tabel, atau dihitung menggunakan beberapa fungsi bawaan perangkat lunak statistik (misalnya Python, R, dll.). Kemudian interval untuk μ akan diberikan oleh X±A*D/√n, di mana X adalah rata-rata sampel yang diperoleh, D adalah standar deviasi.

Catatan: Kami juga mengabaikan pembahasan tentang konsep penting derajat kebebasan, yang penting dalam kaitannya dengan distribusi student. Anda dapat merujuk pada buku statistik yang lebih lengkap untuk memahami konsep ini lebih dalam.

Contoh perhitungan interval kepercayaan untuk berat dan tinggi badan diberikan di notebook pendamping.

p	Rata-rata Berat
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Perhatikan bahwa semakin tinggi probabilitas kepercayaan, semakin lebar interval kepercayaan.

Pengujian Hipotesis

Dalam dataset pemain baseball kita, terdapat berbagai peran pemain, yang dapat dirangkum seperti di bawah ini (lihat notebook pendamping untuk melihat bagaimana tabel ini dihitung):

Peran	Tinggi	Berat	Jumlah
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

Kita dapat melihat bahwa rata-rata tinggi pemain first baseman lebih tinggi dibandingkan second baseman. Oleh karena itu, kita mungkin tergoda untuk menyimpulkan bahwa first baseman lebih tinggi daripada second baseman.

Pernyataan ini disebut hipotesis, karena kita tidak tahu apakah fakta tersebut benar atau tidak.

Namun, tidak selalu jelas apakah kita dapat membuat kesimpulan ini. Dari pembahasan di atas, kita tahu bahwa setiap rata-rata memiliki interval kepercayaan yang terkait, sehingga perbedaan ini mungkin hanya kesalahan statistik. Kita memerlukan cara yang lebih formal untuk menguji hipotesis kita.

Mari kita hitung interval kepercayaan secara terpisah untuk tinggi first baseman dan second baseman:

Kepercayaan	First Baseman	Second Baseman
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Kita dapat melihat bahwa pada tingkat kepercayaan mana pun, interval tidak saling tumpang tindih. Hal ini membuktikan hipotesis kita bahwa first baseman lebih tinggi daripada second baseman.

Secara lebih formal, masalah yang kita selesaikan adalah untuk melihat apakah dua distribusi probabilitas sama, atau setidaknya memiliki parameter yang sama. Bergantung pada distribusinya, kita perlu menggunakan uji yang berbeda untuk itu. Jika kita tahu bahwa distribusi kita normal, kita dapat menerapkan Student t-test.

Dalam Student t-test, kita menghitung apa yang disebut t-value, yang menunjukkan perbedaan antara rata-rata, dengan mempertimbangkan varians. Telah ditunjukkan bahwa t-value mengikuti distribusi student, yang memungkinkan kita mendapatkan nilai ambang untuk tingkat kepercayaan tertentu p (ini dapat dihitung, atau dilihat di tabel numerik). Kita kemudian membandingkan t-value dengan ambang ini untuk menerima atau menolak hipotesis.

Dalam Python, kita dapat menggunakan paket SciPy, yang mencakup fungsi ttest_ind (selain banyak fungsi statistik berguna lainnya!). Fungsi ini menghitung t-value untuk kita, dan juga melakukan pencarian balik nilai p kepercayaan, sehingga kita hanya perlu melihat kepercayaan untuk menarik kesimpulan.

Sebagai contoh, perbandingan kita antara tinggi first baseman dan second baseman memberikan hasil berikut:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

Dalam kasus kita, nilai p sangat rendah, yang berarti ada bukti kuat yang mendukung bahwa first baseman lebih tinggi.

Ada juga berbagai jenis hipotesis lain yang mungkin ingin kita uji, misalnya:

Membuktikan bahwa sampel tertentu mengikuti distribusi tertentu. Dalam kasus kita, kita mengasumsikan bahwa tinggi badan terdistribusi normal, tetapi itu memerlukan verifikasi statistik formal.
Membuktikan bahwa nilai rata-rata sampel sesuai dengan nilai yang telah ditentukan sebelumnya.
Membandingkan rata-rata dari sejumlah sampel (misalnya, perbedaan tingkat kebahagiaan di antara kelompok usia yang berbeda).

Hukum Bilangan Besar dan Teorema Limit Sentral

Salah satu alasan mengapa distribusi normal sangat penting adalah teorema limit sentral. Misalkan kita memiliki sampel besar dari N nilai independen X₁, ..., X_N, yang diambil dari distribusi apa pun dengan rata-rata μ dan varians σ². Kemudian, untuk N yang cukup besar (dengan kata lain, ketika N→∞), rata-rata Σ_iX_i akan terdistribusi normal, dengan rata-rata μ dan varians σ²/N.

Cara lain untuk menafsirkan teorema limit sentral adalah mengatakan bahwa terlepas dari distribusinya, ketika Anda menghitung rata-rata dari jumlah nilai variabel acak apa pun, Anda akan mendapatkan distribusi normal.

Dari teorema limit sentral juga mengikuti bahwa, ketika N→∞, probabilitas rata-rata sampel sama dengan μ menjadi 1. Ini dikenal sebagai hukum bilangan besar.

Kovarians dan Korelasi

Salah satu hal yang dilakukan Data Science adalah menemukan hubungan antara data. Kita mengatakan bahwa dua deret berkorelasi ketika mereka menunjukkan perilaku serupa pada waktu yang sama, yaitu mereka naik/turun secara bersamaan, atau satu deret naik ketika deret lainnya turun dan sebaliknya. Dengan kata lain, tampaknya ada hubungan antara dua deret.

Korelasi tidak selalu menunjukkan hubungan sebab-akibat antara dua deret; terkadang kedua variabel dapat bergantung pada penyebab eksternal, atau bisa jadi murni kebetulan bahwa dua deret berkorelasi. Namun, korelasi matematis yang kuat adalah indikasi baik bahwa dua variabel tersebut saling terkait.

Secara matematis, konsep utama yang menunjukkan hubungan antara dua variabel acak adalah kovarians, yang dihitung seperti ini: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Kita menghitung deviasi kedua variabel dari nilai rata-rata mereka, dan kemudian mengalikan deviasi tersebut. Jika kedua variabel menyimpang bersama, hasil perkalian akan selalu bernilai positif, yang akan menambah kovarians positif. Jika kedua variabel menyimpang tidak sinkron (yaitu satu turun di bawah rata-rata ketika yang lain naik di atas rata-rata), kita akan selalu mendapatkan angka negatif, yang akan menambah kovarians negatif. Jika deviasi tidak saling bergantung, mereka akan menambah sekitar nol.

Nilai absolut kovarians tidak banyak memberi tahu kita tentang seberapa besar korelasi, karena itu bergantung pada besarnya nilai sebenarnya. Untuk menormalkannya, kita dapat membagi kovarians dengan standar deviasi kedua variabel, untuk mendapatkan korelasi. Hal baiknya adalah bahwa korelasi selalu berada dalam rentang [-1,1], di mana 1 menunjukkan korelasi positif yang kuat antara nilai, -1 menunjukkan korelasi negatif yang kuat, dan 0 menunjukkan tidak ada korelasi sama sekali (variabel independen).

Contoh: Kita dapat menghitung korelasi antara berat dan tinggi pemain baseball dari dataset yang disebutkan di atas:

print(np.corrcoef(weights,heights))

Hasilnya, kita mendapatkan matriks korelasi seperti ini:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Matriks korelasi C dapat dihitung untuk sejumlah deret input S₁, ..., S_n. Nilai C_ij adalah korelasi antara S_i dan S_j, dan elemen diagonal selalu 1 (yang juga merupakan korelasi diri dari S_i).

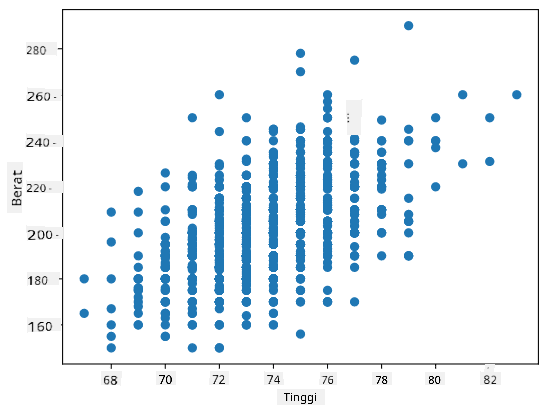
Dalam kasus kita, nilai 0.53 menunjukkan bahwa ada beberapa korelasi antara berat dan tinggi seseorang. Kita juga dapat membuat scatter plot dari satu nilai terhadap nilai lainnya untuk melihat hubungan secara visual:

Lebih banyak contoh korelasi dan kovarians dapat ditemukan di notebook pendamping.

Kesimpulan

Dalam bagian ini, kita telah mempelajari:

sifat statistik dasar data, seperti rata-rata, varians, modus, dan kuartil
berbagai distribusi variabel acak, termasuk distribusi normal
cara menemukan korelasi antara berbagai properti
cara menggunakan perangkat matematika dan statistik untuk membuktikan beberapa hipotesis
cara menghitung interval kepercayaan untuk variabel acak berdasarkan sampel data

Meskipun ini jelas bukan daftar lengkap topik yang ada dalam probabilitas dan statistik, ini seharusnya cukup untuk memberi Anda awal yang baik dalam kursus ini.

🚀 Tantangan

Gunakan kode sampel di notebook untuk menguji hipotesis lain bahwa:

First baseman lebih tua daripada second baseman
First baseman lebih tinggi daripada third baseman
Shortstop lebih tinggi daripada second baseman

Kuis setelah kuliah

Tinjauan & Studi Mandiri

Probabilitas dan statistik adalah topik yang sangat luas sehingga layak mendapatkan kursus tersendiri. Jika Anda tertarik untuk mendalami teori, Anda mungkin ingin melanjutkan membaca beberapa buku berikut:

Carlos Fernandez-Granda dari New York University memiliki catatan kuliah yang bagus Probability and Statistics for Data Science (tersedia online)
Peter dan Andrew Bruce. Practical Statistics for Data Scientists. [kode sampel dalam R].
James D. Miller. Statistics for Data Science [kode sampel dalam R]

Tugas

Studi Diabetes Kecil

Kredit

Pelajaran ini telah dibuat dengan ♥️ oleh Dmitry Soshnikov

Penafian:
Dokumen ini telah diterjemahkan menggunakan layanan penerjemahan AI Co-op Translator. Meskipun kami berusaha untuk memberikan hasil yang akurat, harap diketahui bahwa terjemahan otomatis mungkin mengandung kesalahan atau ketidakakuratan. Dokumen asli dalam bahasa aslinya harus dianggap sebagai sumber yang otoritatif. Untuk informasi yang bersifat kritis, disarankan menggunakan jasa penerjemahan profesional oleh manusia. Kami tidak bertanggung jawab atas kesalahpahaman atau penafsiran yang keliru yang timbul dari penggunaan terjemahan ini.

25 KiB Raw Permalink Blame History Unescape Escape