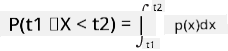25 KiB

Raw Permalink Blame History Unescape Escape

En Kort Introduktion til Statistik og Sandsynlighed


Statistik og Sandsynlighed - Sketchnote af @nitya

Statistik og Sandsynlighedsteori er to nært beslægtede områder inden for matematik, som er meget relevante for datavidenskab. Det er muligt at arbejde med data uden dyb matematisk viden, men det er stadig en fordel at kende nogle grundlæggende begreber. Her præsenterer vi en kort introduktion, der kan hjælpe dig i gang.

Quiz før lektionen

Sandsynlighed og Tilfældige Variable

Sandsynlighed er et tal mellem 0 og 1, der angiver, hvor sandsynligt en begivenhed er. Det defineres som antallet af positive udfald (der fører til begivenheden) divideret med det samlede antal udfald, forudsat at alle udfald er lige sandsynlige. For eksempel, når vi kaster en terning, er sandsynligheden for at få et lige tal 3/6 = 0,5.

Når vi taler om begivenheder, bruger vi tilfældige variable. For eksempel vil den tilfældige variabel, der repræsenterer et tal opnået ved at kaste en terning, tage værdier fra 1 til 6. Sættet af tal fra 1 til 6 kaldes udfaldsrummet. Vi kan tale om sandsynligheden for, at en tilfældig variabel tager en bestemt værdi, for eksempel P(X=3)=1/6.

Den tilfældige variabel i det tidligere eksempel kaldes diskret, fordi den har et tælleligt udfaldsrum, dvs. der er separate værdier, der kan opregnes. Der er tilfælde, hvor udfaldsrummet er et interval af reelle tal eller hele mængden af reelle tal. Sådanne variable kaldes kontinuerlige. Et godt eksempel er tidspunktet, hvor bussen ankommer.

Sandsynlighedsfordeling

For diskrete tilfældige variable er det nemt at beskrive sandsynligheden for hver begivenhed med en funktion P(X). For hver værdi s fra udfaldsrummet S vil den give et tal mellem 0 og 1, sådan at summen af alle værdier af P(X=s) for alle begivenheder vil være 1.

Den mest kendte diskrete fordeling er uniform fordeling, hvor der er et udfaldsrum med N elementer, med lige sandsynlighed på 1/N for hver af dem.

Det er mere udfordrende at beskrive sandsynlighedsfordelingen for en kontinuerlig variabel med værdier trukket fra et interval [a,b] eller hele mængden af reelle tal ℝ. Overvej tilfældet med busankomsttidspunktet. Faktisk er sandsynligheden for, at en bus ankommer præcis på et bestemt tidspunkt t, 0!

Nu ved du, at begivenheder med sandsynlighed 0 sker, og det sker ofte! I det mindste hver gang bussen ankommer!

Vi kan kun tale om sandsynligheden for, at en variabel falder inden for et givet interval af værdier, fx P(t₁≤X<t₂). I dette tilfælde beskrives sandsynlighedsfordelingen af en sandsynlighedstæthedsfunktion p(x), sådan at

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

En kontinuerlig analog til uniform fordeling kaldes kontinuerlig uniform, som er defineret på et endeligt interval. Sandsynligheden for, at værdien X falder inden for et interval af længde l, er proportional med l og stiger op til 1.

En anden vigtig fordeling er normal fordeling, som vi vil tale mere om nedenfor.

Middelværdi, Varians og Standardafvigelse

Antag, at vi trækker en sekvens af n prøver af en tilfældig variabel X: x₁, x₂, ..., x_n. Vi kan definere middelværdi (eller aritmetisk gennemsnit) af sekvensen på traditionel vis som (x₁+x₂+x_n)/n. Når vi øger størrelsen af prøven (dvs. tager grænsen med n→∞), vil vi opnå middelværdien (også kaldet forventning) af fordelingen. Vi vil betegne forventningen med E(x).

Det kan vises, at for enhver diskret fordeling med værdier {x₁, x₂, ..., x_N} og tilsvarende sandsynligheder p₁, p₂, ..., p_N, vil forventningen være E(X)=x₁p₁+x₂p₂+...+x_Np_N.

For at identificere, hvor spredte værdierne er, kan vi beregne variansen σ² = ∑(x_i - μ)²/n, hvor μ er middelværdien af sekvensen. Værdien σ kaldes standardafvigelse, og σ² kaldes varians.

Typetal, Median og Kvartiler

Nogle gange repræsenterer middelværdien ikke tilstrækkeligt den "typiske" værdi for data. For eksempel, når der er nogle ekstreme værdier, der er helt uden for rækkevidde, kan de påvirke middelværdien. En anden god indikator er medianen, en værdi sådan, at halvdelen af datapunkterne er lavere end den, og den anden halvdel - højere.

For at hjælpe os med at forstå datafordelingen er det nyttigt at tale om kvartiler:

Første kvartil, eller Q1, er en værdi, sådan at 25% af dataene ligger under den
Tredje kvartil, eller Q3, er en værdi, sådan at 75% af dataene ligger under den

Grafisk kan vi repræsentere forholdet mellem median og kvartiler i et diagram kaldet box plot:

Her beregner vi også interkvartilområdet IQR=Q3-Q1 og såkaldte outliers - værdier, der ligger uden for grænserne [Q1-1.5IQR,Q3+1.5IQR].

For en endelig fordeling, der indeholder et lille antal mulige værdier, er en god "typisk" værdi den, der forekommer hyppigst, hvilket kaldes typetal. Det anvendes ofte på kategoriske data, såsom farver. Overvej en situation, hvor vi har to grupper af mennesker - nogle, der stærkt foretrækker rød, og andre, der foretrækker blå. Hvis vi koder farver med tal, vil middelværdien for en favoritfarve være et sted i det orange-grønne spektrum, hvilket ikke angiver den faktiske præference for nogen af grupperne. Typetallet vil dog være enten en af farverne eller begge farver, hvis antallet af mennesker, der stemmer for dem, er lige (i dette tilfælde kalder vi prøven multimodal).

Data fra Virkeligheden

Når vi analyserer data fra virkeligheden, er de ofte ikke tilfældige variable i den forstand, at vi ikke udfører eksperimenter med ukendt resultat. For eksempel, overvej et hold af baseballspillere og deres kropsdata, såsom højde, vægt og alder. Disse tal er ikke præcis tilfældige, men vi kan stadig anvende de samme matematiske begreber. For eksempel kan en sekvens af folks vægte betragtes som en sekvens af værdier trukket fra en tilfældig variabel. Nedenfor er sekvensen af vægte for faktiske baseballspillere fra Major League Baseball, taget fra dette datasæt (for din bekvemmelighed vises kun de første 20 værdier):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Note: For at se et eksempel på arbejde med dette datasæt, kig på den tilhørende notebook. Der er også en række udfordringer gennem denne lektion, og du kan fuldføre dem ved at tilføje noget kode til den notebook. Hvis du ikke er sikker på, hvordan man arbejder med data, skal du ikke bekymre dig - vi vender tilbage til at arbejde med data ved hjælp af Python senere. Hvis du ikke ved, hvordan man kører kode i Jupyter Notebook, kan du kigge på denne artikel.

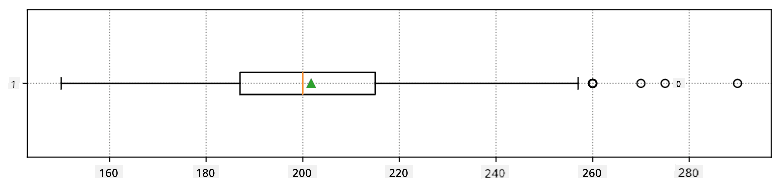
Her er box plottet, der viser middelværdi, median og kvartiler for vores data:

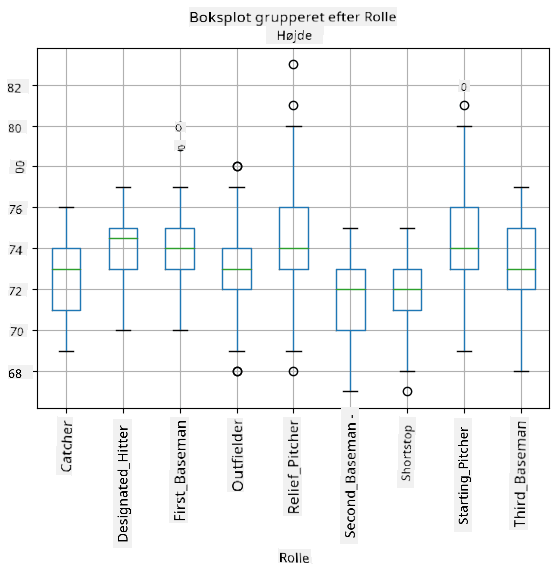
Da vores data indeholder information om forskellige spiller roller, kan vi også lave box plottet efter rolle - det vil give os en idé om, hvordan parameterværdierne varierer på tværs af roller. Denne gang vil vi overveje højde:

Dette diagram antyder, at gennemsnitligt er højden af første basemen højere end højden af anden basemen. Senere i denne lektion vil vi lære, hvordan vi kan teste denne hypotese mere formelt, og hvordan vi kan demonstrere, at vores data er statistisk signifikante for at vise dette.

Når vi arbejder med data fra virkeligheden, antager vi, at alle datapunkter er prøver trukket fra en sandsynlighedsfordeling. Denne antagelse giver os mulighed for at anvende maskinlæringsteknikker og bygge fungerende forudsigelsesmodeller.

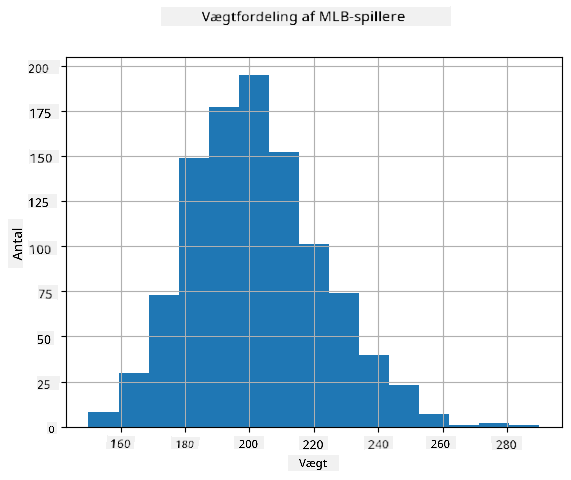
For at se, hvordan fordelingen af vores data er, kan vi plotte en graf kaldet et histogram. X-aksen vil indeholde et antal forskellige vægtintervaller (såkaldte bins), og den lodrette akse vil vise antallet af gange, vores tilfældige variabelprøve var inden for et givet interval.

Fra dette histogram kan du se, at alle værdier er centreret omkring en bestemt gennemsnitsvægt, og jo længere vi bevæger os fra den vægt - jo færre vægte af den værdi støder vi på. Dvs., det er meget usandsynligt, at vægten af en baseballspiller vil være meget forskellig fra gennemsnitsvægten. Variansen af vægtene viser, i hvilket omfang vægtene sandsynligvis vil afvige fra gennemsnittet.

Hvis vi tager vægtene af andre mennesker, ikke fra baseballligaen, vil fordelingen sandsynligvis være anderledes. Dog vil formen af fordelingen være den samme, men middelværdien og variansen vil ændre sig. Så hvis vi træner vores model på baseballspillere, vil den sandsynligvis give forkerte resultater, når den anvendes på studerende på et universitet, fordi den underliggende fordeling er anderledes.

Normalfordeling

Fordelingen af vægte, som vi har set ovenfor, er meget typisk, og mange målinger fra virkeligheden følger samme type fordeling, men med forskellige middelværdier og varians. Denne fordeling kaldes normalfordeling, og den spiller en meget vigtig rolle i statistik.

At bruge normalfordeling er en korrekt måde at generere tilfældige vægte af potentielle baseballspillere. Når vi kender gennemsnitsvægten mean og standardafvigelsen std, kan vi generere 1000 vægtprøver på følgende måde:

samples = np.random.normal(mean,std,1000)

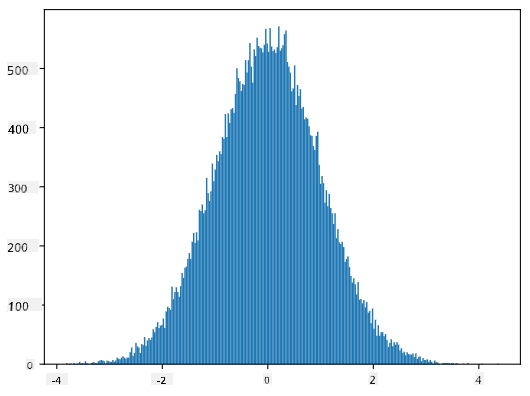
Hvis vi plotter histogrammet for de genererede prøver, vil vi se et billede, der ligner det, der er vist ovenfor. Og hvis vi øger antallet af prøver og antallet af bins, kan vi generere et billede af en normalfordeling, der er tættere på det ideelle:

Normalfordeling med mean=0 og std.dev=1

Konfidensintervaller

Når vi taler om vægtene af baseballspillere, antager vi, at der er en bestemt tilfældig variabel W, der svarer til den ideelle sandsynlighedsfordeling af vægtene for alle baseballspillere (den såkaldte population). Vores sekvens af vægte svarer til et udsnit af alle baseballspillere, som vi kalder prøve. Et interessant spørgsmål er, om vi kan kende parametrene for fordelingen af W, dvs. middelværdien og variansen af populationen?

Det nemmeste svar ville være at beregne middelværdien og variansen af vores prøve. Dog kunne det ske, at vores tilfældige prøve ikke nøjagtigt repræsenterer den komplette population. Derfor giver det mening at tale om konfidensintervaller.

Konfidensinterval er en estimering af den sande middelværdi for populationen baseret på vores stikprøve, som er nøjagtig med en vis sandsynlighed (eller konfidensniveau). Antag, at vi har en stikprøve X₁, ..., X_n fra vores fordeling. Hver gang vi trækker en stikprøve fra vores fordeling, vil vi ende med en forskellig middelværdi μ. Derfor kan μ betragtes som en stokastisk variabel. Et konfidensinterval med konfidens p er et par værdier (L_p,R_p), sådan at P(L_p≤μ≤R_p) = p, dvs. sandsynligheden for, at den målte middelværdi falder inden for intervallet, er lig med p.

Det går ud over vores korte introduktion at diskutere i detaljer, hvordan disse konfidensintervaller beregnes. Flere detaljer kan findes på Wikipedia. Kort sagt definerer vi fordelingen af den beregnede stikprøvemiddelværdi i forhold til den sande middelværdi af populationen, hvilket kaldes studentfordeling.

Interessant fakta: Studentfordelingen er opkaldt efter matematikeren William Sealy Gosset, som udgav sin artikel under pseudonymet "Student". Han arbejdede på Guinness-bryggeriet, og ifølge en af versionerne ønskede hans arbejdsgiver ikke, at offentligheden skulle vide, at de brugte statistiske tests til at bestemme kvaliteten af råmaterialer.

Hvis vi ønsker at estimere middelværdien μ af vores population med konfidens p, skal vi tage (1-p)/2-percentilen af en Studentfordeling A, som enten kan tages fra tabeller eller beregnes ved hjælp af indbyggede funktioner i statistisk software (fx Python, R osv.). Derefter vil intervallet for μ være givet ved X±A*D/√n, hvor X er den opnåede middelværdi af stikprøven, og D er standardafvigelsen.

Bemærk: Vi udelader også diskussionen om et vigtigt begreb, frihedsgrader, som er vigtigt i relation til Studentfordelingen. Du kan henvise til mere komplette bøger om statistik for at forstå dette begreb dybere.

Et eksempel på beregning af konfidensinterval for vægt og højde findes i de tilhørende notebooks.

p	Vægtmiddelværdi
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Bemærk, at jo højere konfidenssandsynligheden er, desto bredere er konfidensintervallet.

Hypotesetestning

I vores dataset med baseballspillere er der forskellige spillerroller, som kan opsummeres nedenfor (se den tilhørende notebook for at se, hvordan denne tabel kan beregnes):

Rolle	Højde	Vægt	Antal
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

Vi kan bemærke, at middelhøjden for first basemen er højere end for second basemen. Derfor kan vi være fristet til at konkludere, at first basemen er højere end second basemen.

Denne erklæring kaldes en hypotese, fordi vi ikke ved, om det faktisk er sandt eller ej.

Det er dog ikke altid indlysende, om vi kan drage denne konklusion. Fra diskussionen ovenfor ved vi, at hver middelværdi har et tilhørende konfidensinterval, og derfor kan denne forskel blot være en statistisk fejl. Vi har brug for en mere formel metode til at teste vores hypotese.

Lad os beregne konfidensintervaller separat for højderne af first og second basemen:

Konfidens	First Basemen	Second Basemen
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

Vi kan se, at under ingen konfidens overlapper intervallerne. Det beviser vores hypotese om, at first basemen er højere end second basemen.

Mere formelt er problemet, vi løser, at undersøge, om to sandsynlighedsfordelinger er ens, eller i det mindste har de samme parametre. Afhængigt af fordelingen skal vi bruge forskellige tests til det. Hvis vi ved, at vores fordelinger er normale, kan vi anvende Student t-test.

I Student t-test beregner vi den såkaldte t-værdi, som angiver forskellen mellem middelværdierne under hensyntagen til variansen. Det er påvist, at t-værdien følger studentfordelingen, hvilket giver os mulighed for at finde tærskelværdien for et givet konfidensniveau p (dette kan beregnes eller findes i numeriske tabeller). Vi sammenligner derefter t-værdien med denne tærskel for at godkende eller afvise hypotesen.

I Python kan vi bruge SciPy-pakken, som inkluderer funktionen ttest_ind (ud over mange andre nyttige statistiske funktioner!). Den beregner t-værdien for os og udfører også den omvendte opslagning af konfidens p-værdien, så vi blot kan se på konfidensen for at drage konklusionen.

For eksempel giver vores sammenligning mellem højderne af first og second basemen os følgende resultater:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

I vores tilfælde er p-værdien meget lav, hvilket betyder, at der er stærke beviser for, at first basemen er højere.

Der er også forskellige andre typer hypoteser, som vi måske ønsker at teste, for eksempel:

At bevise, at en given stikprøve følger en bestemt fordeling. I vores tilfælde har vi antaget, at højderne er normalt fordelt, men det kræver formel statistisk verifikation.
At bevise, at middelværdien af en stikprøve svarer til en foruddefineret værdi.
At sammenligne middelværdierne af flere stikprøver (fx hvad er forskellen i lykkefølelse blandt forskellige aldersgrupper).

Lov om store tal og central grænseværdisætning

En af grundene til, at normalfordelingen er så vigtig, er den såkaldte central grænseværdisætning. Antag, at vi har en stor stikprøve af uafhængige N værdier X₁, ..., X_N, udtaget fra en hvilken som helst fordeling med middelværdi μ og varians σ². Så, for tilstrækkeligt store N (med andre ord, når N→∞), vil middelværdien Σ_iX_i være normalt fordelt med middelværdi μ og varians σ²/N.

En anden måde at fortolke den centrale grænseværdisætning på er at sige, at uanset fordelingen, når du beregner middelværdien af summen af vilkårlige stokastiske variabelværdier, ender du med en normalfordeling.

Fra den centrale grænseværdisætning følger det også, at når N→∞, bliver sandsynligheden for, at stikprøvemiddelværdien er lig med μ, 1. Dette er kendt som loven om store tal.

Kovarians og korrelation

En af de ting, Data Science gør, er at finde relationer mellem data. Vi siger, at to sekvenser korrelerer, når de udviser lignende adfærd på samme tid, dvs. de enten stiger/falder samtidig, eller én sekvens stiger, når en anden falder og omvendt. Med andre ord ser der ud til at være en relation mellem to sekvenser.

Korrelation indikerer ikke nødvendigvis en årsagssammenhæng mellem to sekvenser; nogle gange kan begge variabler afhænge af en ekstern årsag, eller det kan være rent tilfældigt, at de to sekvenser korrelerer. Dog er stærk matematisk korrelation en god indikation på, at to variabler på en eller anden måde er forbundet.

Matematisk er det primære begreb, der viser relationen mellem to stokastiske variabler, kovarians, som beregnes sådan: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Vi beregner afvigelsen af begge variabler fra deres middelværdier og derefter produktet af disse afvigelser. Hvis begge variabler afviger sammen, vil produktet altid være en positiv værdi, der vil summere til positiv kovarians. Hvis begge variabler afviger ude af sync (dvs. én falder under gennemsnittet, når en anden stiger over gennemsnittet), vil vi altid få negative tal, der vil summere til negativ kovarians. Hvis afvigelserne ikke er afhængige, vil de summere til cirka nul.

Den absolutte værdi af kovarians fortæller os ikke meget om, hvor stor korrelationen er, fordi den afhænger af størrelsen af de faktiske værdier. For at normalisere den kan vi dividere kovarians med standardafvigelsen af begge variabler for at få korrelation. Det gode ved korrelation er, at den altid ligger i intervallet [-1,1], hvor 1 indikerer stærk positiv korrelation mellem værdier, -1 - stærk negativ korrelation, og 0 - ingen korrelation overhovedet (variablerne er uafhængige).

Eksempel: Vi kan beregne korrelationen mellem vægt og højde for baseballspillere fra det nævnte dataset:

print(np.corrcoef(weights,heights))

Som resultat får vi korrelationsmatrix som denne:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Korrelationsmatrix C kan beregnes for et vilkårligt antal inputsekvenser S₁, ..., S_n. Værdien af C_ij er korrelationen mellem S_i og S_j, og diagonalelementerne er altid 1 (hvilket også er selvkorrelationen af S_i).

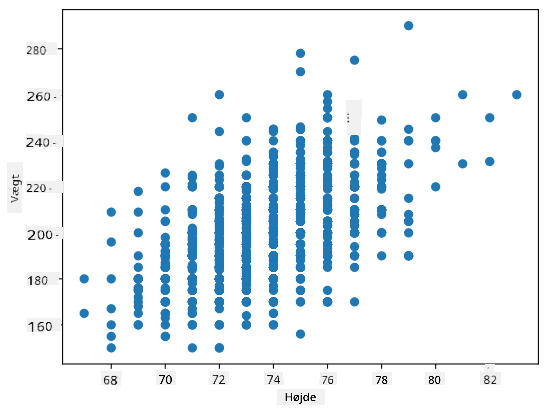
I vores tilfælde indikerer værdien 0.53, at der er en vis korrelation mellem en persons vægt og højde. Vi kan også lave et scatterplot af én værdi mod den anden for at se relationen visuelt:

Flere eksempler på korrelation og kovarians kan findes i den tilhørende notebook.

Konklusion

I denne sektion har vi lært:

grundlæggende statistiske egenskaber ved data, såsom middelværdi, varians, typetal og kvartiler
forskellige fordelinger af stokastiske variabler, herunder normalfordeling
hvordan man finder korrelation mellem forskellige egenskaber
hvordan man bruger matematiske og statistiske metoder til at bevise hypoteser
hvordan man beregner konfidensintervaller for stokastiske variabler givet en stikprøve

Selvom dette bestemt ikke er en udtømmende liste over emner inden for sandsynlighed og statistik, bør det være nok til at give dig en god start på dette kursus.

🚀 Udfordring

Brug eksempelkoden i notebooken til at teste andre hypoteser:

First basemen er ældre end second basemen
First basemen er højere end third basemen
Shortstops er højere end second basemen

Quiz efter lektionen

Gennemgang & Selvstudie

Sandsynlighed og statistik er et så bredt emne, at det fortjener sit eget kursus. Hvis du er interesseret i at gå dybere ind i teorien, kan du overveje at læse nogle af følgende bøger:

Carlos Fernandez-Granda fra New York University har fremragende noter Probability and Statistics for Data Science (tilgængelig online)
Peter og Andrew Bruce. Practical Statistics for Data Scientists. [eksempelkode i R].
James D. Miller. Statistics for Data Science [eksempelkode i R]

Opgave

Small Diabetes Study

Credits

Denne lektion er skrevet med ♥️ af Dmitry Soshnikov

Ansvarsfraskrivelse:
Dette dokument er blevet oversat ved hjælp af AI-oversættelsestjenesten Co-op Translator. Selvom vi bestræber os på nøjagtighed, skal du være opmærksom på, at automatiserede oversættelser kan indeholde fejl eller unøjagtigheder. Det originale dokument på dets oprindelige sprog bør betragtes som den autoritative kilde. For kritisk information anbefales professionel menneskelig oversættelse. Vi er ikke ansvarlige for eventuelle misforståelser eller fejltolkninger, der opstår som følge af brugen af denne oversættelse.

25 KiB Raw Permalink Blame History Unescape Escape