10 KiB

Raw Blame History Unescape Escape

必备数学基础

函数

函数的定义：

y = f(x) 其中x是自变量，y是因变量。y随着x变化

几种特性：

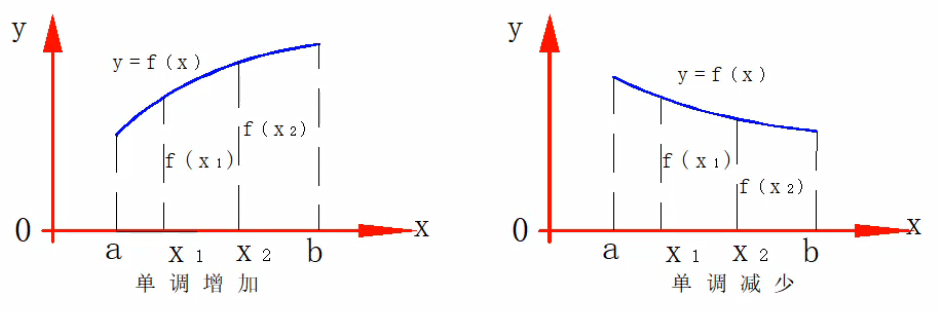
奇偶性、周期性、单调性（如下图）

极限：

按照一定次数排列的数：x1，x2，...，xn，其中xn叫做通项
对于数列｛xn｝,当n无限增大时，其通项无限接近于一个常数A，则称该数列以A为极限或称数列收敛于A。

导数：

都有对应的结果，不用死记硬背，查就行了，如(C)' = 0 或者(sin x)' = cos x

方向导数（引出梯度）

在函数定义域的内点，对某一方向求导得到的导数。

常规数学中，所有问题都有一个解。而机器学习当中，求解很难或者没有解，我们只能不断逼近这个最优解。

问题一：蚂蚁沿着什么方向跑路不被火烧，能活下来（二维平面）


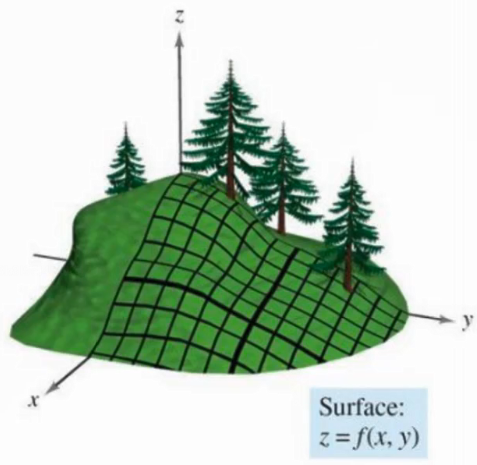
函数：z = f(x,y)


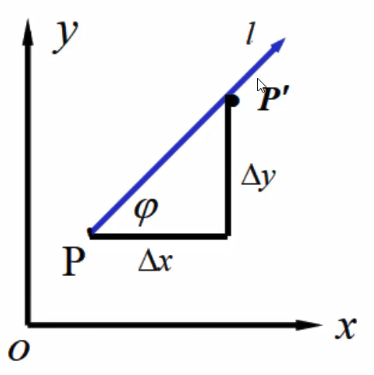
|pp'| = p = \sqrt{(\Delta x) ^ 2 + (\Delta y) ^ 2}


\Delta z = f(x + \Delta x, y + \Delta y)-f(x,y)

蚂蚁沿着任意方向都可以活，最优的是沿着对角方向L，z是函数变化，也就是图中的φ。

三维平面的方向导数公式：


定理：如果函数z=f(x,y)在点P(x,y)是可微分的，那么在该点沿任意方向L的方向导数都存在。


\frac {\delta f}{\delta l} = \frac {\delta f}{\delta x}cos\varphi + \frac {\delta f}{\delta y} sin \varphi


\varphi 是X轴到L的角度

求一个方向导数具体的值：


求函数z=xe^{2y}在点P(1,0)处沿从点P(1,0)到点Q(2,-1)的方向的方向导数.


解\quad \quad 这里方向\vec l即为 \vec{PQ}={1,-1},故X轴到方向\vec l的转角\varphi = -\frac {\pi}{4}.


\because \frac {\delta z}{\delta x}|_{(1,0)} = e^{2y}|_{(1,0)}=1;
 \frac {\delta z}{\delta y}|_{(1,0)} = 2xe^{2y}|_{(1,0)}=2,


所求方向导数


\frac {\delta z}{\delta l}=cos(-\frac{\pi}{4})+2sin(-\frac{\pi}{4})=-\frac{\sqrt 2}{2}.

梯度

是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。


函数：z=f(x,y)在平面域内具有连续的一阶偏导数，对于其中每一个点P(x,y)都有向量\frac {\delta f}{\delta x}\vec i + \frac {\delta f}{\delta y}\vec j


则称其为函数在点P的梯度。


gradf(x,y)=\frac {\delta f}{\delta x}\vec i + \frac {\delta f}{\delta y}\vec j


\vec e = cos\varphi\vec i + sin\varphi\vec j是方向L上的单位向量


\frac {\delta f}{\delta l}=\frac {\delta f}{\delta x}cos\varphi+\frac{\delta f}{\delta y}sin\varphi=\{\frac{\delta f}{\delta x}, \frac{\delta f}{\delta y}\}·\{cos\varphi, sin\varphi\}


=gradf(x,y)·\vec e = |gradf(x,y)|cos\theta \quad \theta=(gradf(x,y),\vec e)

根据上面的梯度导数，和方向导数的区别就在多了个cosθ，θ充当梯度和方向导数之间的关系


只有当cos(gradf(x,y),\vec e)=1,\frac{\delta f}{\delta l}才有最大值。

函数在某点的梯度是一个向量，它的方向与方向导数最大值取得的方向一致。

其大小正好是最大的方向导数

注意，只有θ=0，cos导数才能=1，梯度才能取得最大值，也就是那个方向。而沿着反方向就是最小值也就是梯度下降。

求一个具体值，最大梯度方向和最小梯度方向：


设u=xyz+z^2+5,求gradu,并求在点M(0,1,-1)处方向导数的最大(小)值


\because \frac{\delta u}{\delta x}=yz, \frac{\delta u}{\delta y}=xz,\frac{\delta u}{\delta z}=xy+2z,


\therefore gradu|_{(0,1,-1)}=(yz,xz,xy+2z)|_{(0,1,-1)}=(-1,0)


从而最大值\quad max\{\frac{\delta u}{\delta l}|_M\}=||gradu||=\sqrt 5


最小值\quad min\{\frac{\delta u}{\delta l}|_M\}=-||gradu||=-\sqrt 5

注：得出的结果(-1,0,2)，求解：((-1^2) + (0^2) + (-2^2)) = √5，前面都是x的平方，所以结果也需要开根号。

微积分

很多的微分积起来

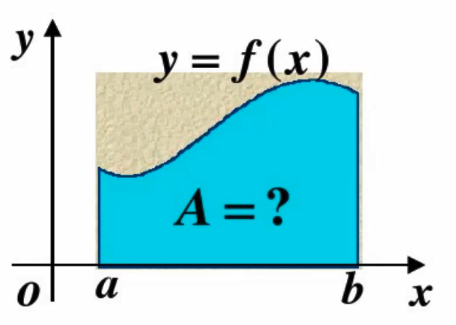
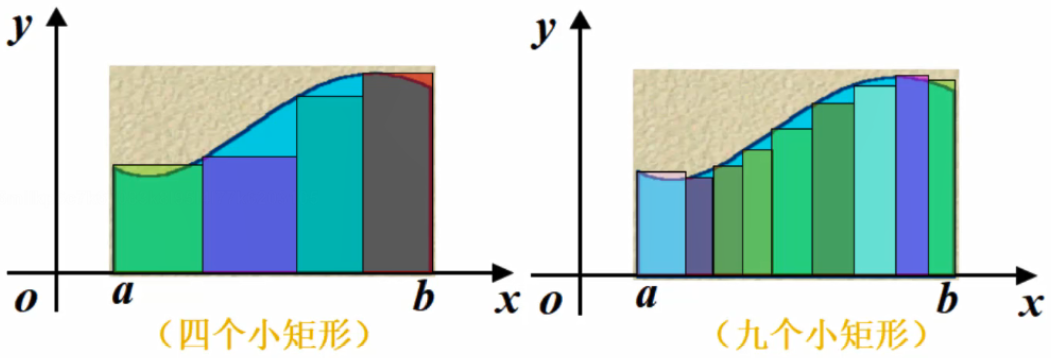
如何求A面积的值

以直代曲：

对于矩形，我们可以轻松求得其面积，能否用矩形代替曲线形状呢？
应该用多少个矩形来代替？

越小的矩形，越覆盖，然后求每个矩形的面积。


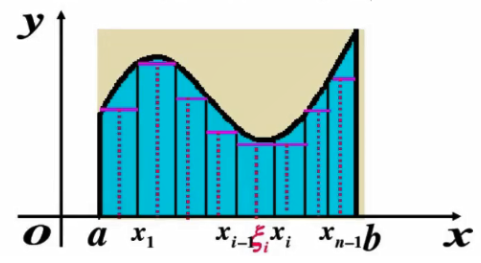
在ab之间插入若干个点，得到n个小区间。


每个小矩形面积为：A_i=f(\xi
_i)\Delta x_i近似得到曲线面积：A\approx \sum^{n}_{i=1}f(\xi_i)\Delta x_i


当分割无限加细，每个小区间的最大长度为\lambda，此时\lambda → 0


曲边面积：A=lim_{\lambda→0}\sum^n_{i=1}f(\xi_i)\Delta x_i

注意每个小区间的最大长度为λ，而λ无限接近于0时，那么曲边的面积我们就可以得出，当然这里的近似表达是极限，无限接近的极限。

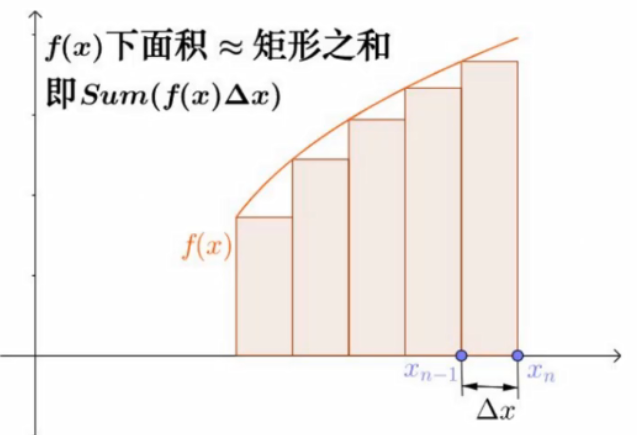
求和：

我们需要尽可能的将每一个矩形的底边无穷小


莱布尼茨为了体现求和的感觉，把S拉长了，简写成\int f(x)dx \quad Sum(f(x)\Delta x) => \int_{um}f(x)dx

将上面的所有矩阵求和，∫ = sum，求和的意思

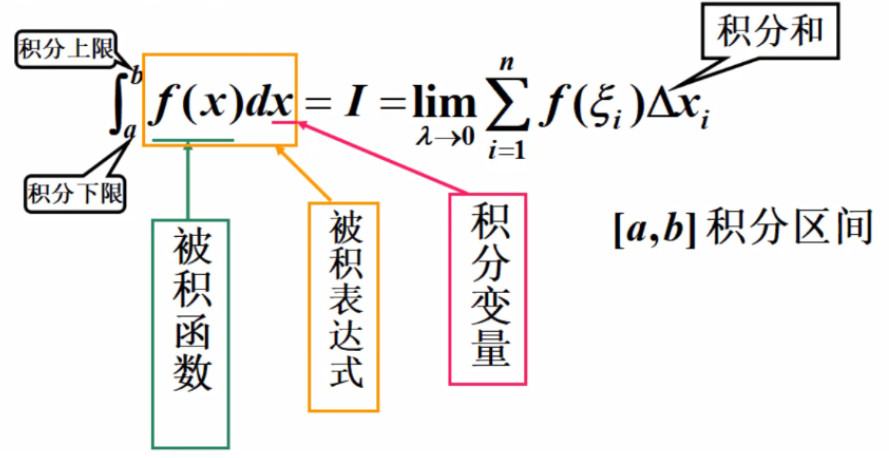
定积分:


当||\Delta x||→0时，总和S总数趋于确定的极限l，则称极限l为函数f(x)在曲线[a,b]上的定积分

矩阵和特征

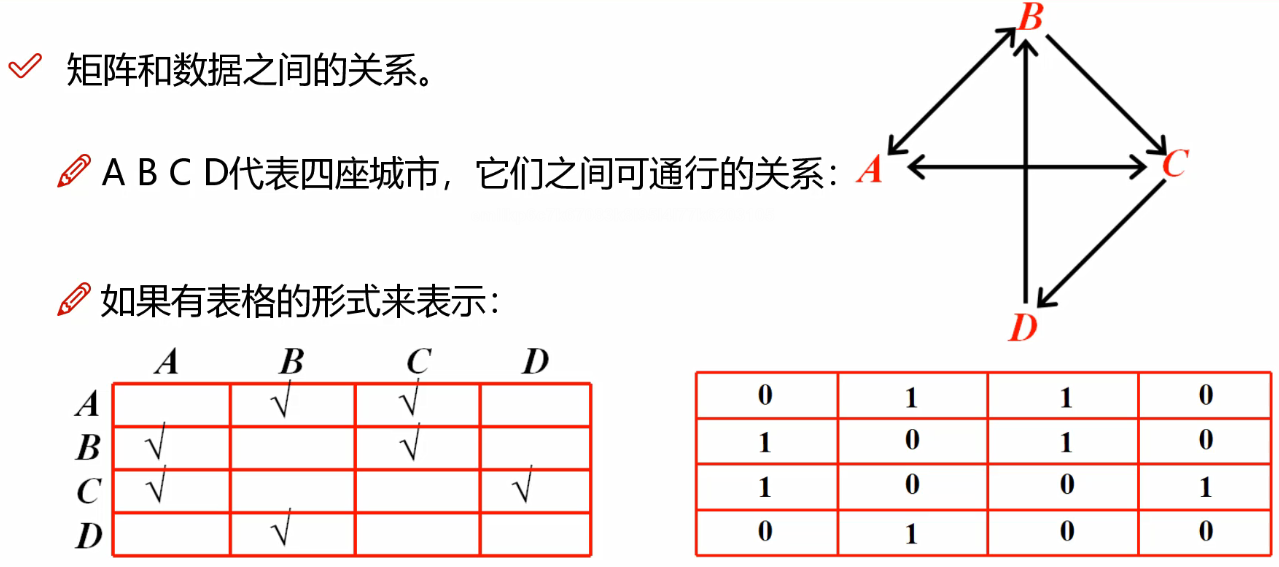
矩阵：

拿到数据后，数据就长如下样子，有行有列

左图√表示A可以到B和C，如右上图，再把√号改成0/1以存储在数据里面，就如右下图

几种特别的矩阵：


上三角矩阵
\left[
\matrix{
  a_{11} & a_{12} & ... &a_{1n}\\
  0 & a_{22} & ... &a_{2n}\\
  ⋮ & ⋮ &⋮&⋮\\
  0 & 0 & ... &a_{nm}\\
}
\right]
\quad 下三角矩阵
\left[
\matrix{
  a_{11} & 0 & ...& 0\\
  a_{21} & a_{22} & ... &0\\
  ⋮ & ⋮ & ⋮ & ⋮ \\
  a_{n1} & a_{n2} & ... &a_{nm}\\
}
\right]

上三角部分有值，和下三角部分有值


对角阵
\left[
\matrix{
  \lambda_1 & 0 & ... &0\\
  0 & \lambda_2 & ... &0\\
  ⋮ & ⋮ & &⋮\\
  0 & 0 & ... &\lambda_n\\
}
\right]
\quad 单位矩阵
\left[
\matrix{
  1 & 0 & ...& 0\\
  0 & 1 & ... &0\\
  ⋮ & ⋮ & ⋮ & ⋮ \\
  0 & 0 & ... &1\\
}
\right]

对角阵：对角有值且可以是任意值，单位矩阵：对角有值且相同


两个矩阵行列数相同的时候称为同型矩阵
\left[
\matrix{
  1 & 2\\
  6 & 7\\
  4 & 3 
}
\right]
与
\left[
\matrix{
  12 & 2\\
  9 & 1\\
  10 & 6 
}
\right]

同型矩阵：行列相同。矩阵相等：行列相同且里面的值一样

SVD矩阵分解

数据行列可能很大，如电商行业100万客户（行），有1万的商品（特征），用一组数据表达就是

客户ID	商品1	商品2	...	商品1万
xxx1	1（表示买过一次）	0	...	5
xxx2	0	1	...	0
...	5	10	...	0
xxx100万	...	...	...	...

那么来一个客户，就是直接多1万列表示，这样的数据是非常稀疏的，我们可以分解成A表100万客户，100个特征，而这100个特征对应这那B表的1万个商品，也就是一个表变成A表和B表，且两者关联。

这就需要用到SVD矩阵。

离散和连续型数据

离散型是有限多个的，比如10个台阶，只可能是其中的一个台阶，一个确定的结果。

连续型则可能是任意的值，没办法确定是哪个台阶。

离散型随机变量概率分布

找到离散型随机变量X的所有可能取值

得到离散型随机变量取这些值的概率


f(x_i)=P(X=x_i)为离散型随机变量的概率函数

连续型随机变量概率分布

密度：一个物体，如果问其中一个点的质量是多少？这该怎么求？

由于这个点实在太小了，那么质量就为0了，但是其中的一大块是由

很多个点组成的，这时我们就可以根据密度来求其质量了
X为连续随机变量，X在任意区间(a,b]上的概率可以表示为：


P(a<X\leq b)=\int_a^bf(x)dx
\quad 其中f(x)就叫做X的概率密度函数，也可以简单叫做密度

还有一种方法是把每个值划分在不同区间，变成离散型，但如果有新数据进来就要再划分区间导致区间越来越多。

简单随机抽样

抽取的样本满足两点

样本X1，X2...Xn是相互独立的随机变量。
样本X1，X2...Xn与总体X同分布。


联合分布函数：F(x_1,x_2,...,x_n)=\prod_{i=1}^nF(x_i)


联合概率密度：f(x_1,x_2,...,x_n)=\prod_{i=1}^nf(x_i)

极大似然估计

找到最有可能的那个

```
构造似然函数：L(\theta)
```


对似然函数取对数：lnL(\theta)

```
求偏导：\frac {dlnL}{d\theta}=0
```
```
求解得到\theta值
```

第一步构造函数；第二步取对数，对数后的值容易取且极值点还是那个位置；第三步求偏导；得到θ

求一个具体的值：

设 X 服从参数 λ(λ>0) 的泊松分布，x1,x2,...,xn 是来自 X 的一个样本值，求λ的极大似然估计值


因为X的分布律为P\{X=x\}=\frac{\lambda^x}{x!}e^{-\lambda},(x=0,1,2,...,n)


所以\lambda的似然函数为L(\lambda)=\prod^n_{i=1}(\frac{\lambda^{x_i}}{x_i!}e^{-\lambda})=e^{-n\lambda}\frac{\lambda^{\sum^n_{i=1}x_i}}{\prod^n_{i=1}(x_i!)},


lnL(\lambda)=-n\lambda+(\sum^n_{i=1}x_i)ln\lambda-\sum^n_{i=1}(x_i!),


令\frac{d}{d\lambda}lnL(\lambda)=-n+\frac{\sum^n_{i=1}x_i}{\lambda}=0


解得\lambda的极大似然估计值为\hat{\lambda}=\frac{1}{n}\sum_{i=1}^nx_i=\overline{x}

10 KiB Raw Blame History Unescape Escape