5.7 KiB

Raw Blame History Unescape Escape

第七章——前馈神经网络

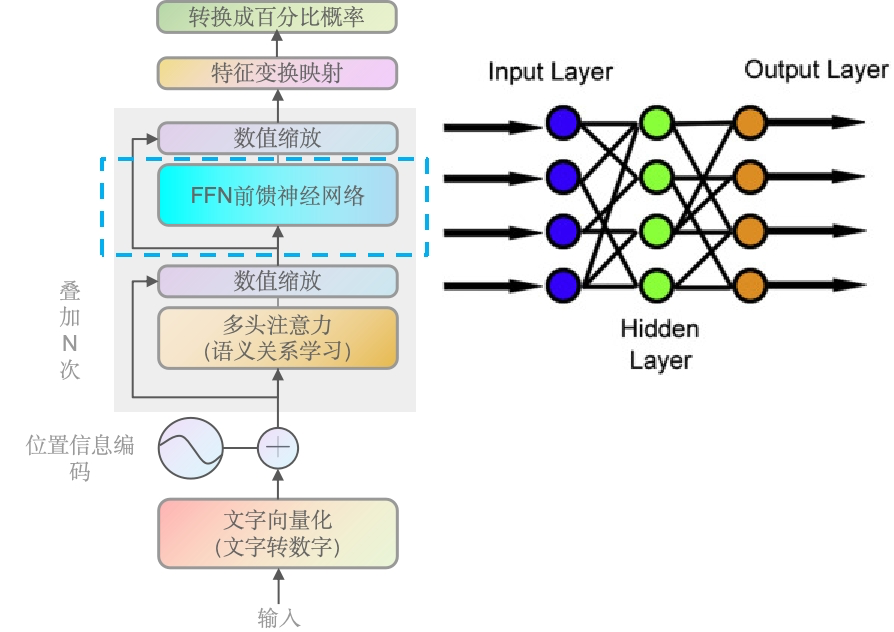
前言

在A Neural Network Playground这个网址玩过的应该对神经网络有了基本的了解，大部分情况下，随着层数跟神经元的增加，结果一般也会变好，即正相关，但同时也意味着更多的资源投入等。我们对神经网络这块讲的会比较简单，因为更底层的原理短时间无法讲明白，大家了解稍微深一点即可。

GPT-2里的前馈神经网络

源代码如下。需要看的点击前面链接跳转

def conv1d(x, scope, nf, *, w_init_stdev=0.02):
    with tf.variable_scope(scope):
        *start, nx = shape_list(x)
        w = tf.get_variable('w', [1, nx, nf], initializer=tf.random_normal_initializer(stddev=w_init_stdev))  # 训练中更新的权重w
        b = tf.get_variable('b', [nf], initializer=tf.constant_initializer(0))  # 训练中更新的偏值项b
        c = tf.reshape(tf.matmul(tf.reshape(x, [-1, nx]), tf.reshape(w, [-1, nf]))+b, start+[nf])
        return c
      
def mlp(x, scope, n_state, *, hparams):
    with tf.variable_scope(scope):
        nx = x.shape[-1].value
        h = gelu(conv1d(x, 'c_fc', n_state))  # 第一层是一个线性变换，后面跟着一个GELU激活函数
        h2 = conv1d(h, 'c_proj', nx)  # 二层是另一个线性变换，将数据从隐藏层的维度映射回原始维度
        return h2

可以看到上面是非常简单的两层线性变换，而且没有其它隐藏层。

FFNN 在 Transformer 中的作用是为了引入非线性并增加模型的表达能力。多头注意力机制虽然能够捕捉输入序列中的长距离依赖关系，但它本身是一个线性操作。FFNN 通过在注意力机制之后添加非线性变换，使得模型能够学习更复杂的特征表示。

神经网络demo

我们来手动推一个简单的神经网络并更新权重，用一个单层神经网络做例子。这个网络将只有一个输入、一个输出和一个权重（没有偏值项b）。我们将使用均方误差作为损失函数，并通过梯度下降来更新权重。

输入 (x)  输出 (y)
   1       2
   2       4
   3       6

我们的目标是训练一个模型来预测输出y，给定输入x。我们的模型是一个线性模型：y_pred = w * x。

初始化权重 w 为 0.5，学习率 lr 为 0.01。我们将手动进行3次迭代的权重更新。

迭代 1:

前向传播：计算预测值

y_pred = w * x = 0.5 * 1 = 0.5  (对于第一个样本)

计算损失：使用均方误差
```
loss = (y_pred - y)^2 = (0.5 - 2)^2 = 2.25
```
这时候可以看到损失是2.25，一个很大的值，神经网络的最终目的是要降为无限接近于0甚至0（当然一般是达不到0 的，达到的情况下只有可能是错了的）。
反向传播：计算损失关于权重w的梯度
```
dloss/dw = 2 * (y_pred - y) * x = 2 * (0.5 - 2) * 1 = -3
```
我们需要通过反向传播来更新权重。

更新权重：

w = w - lr * dloss/dw = 0.5 - 0.01 * (-3) = 0.53

迭代 2:

重复上述步骤，使用更新后的权重：

前向传播：
```
y_pred = w * x = 0.53 * 1 = 0.53
```
计算损失：
```
loss = (0.53 - 2)^2 = 2.14
```
可以看到loss值下降了，2.25下降为2.14，但是还不够，我们的目标是无限接近0。
反向传播：
```
dloss/dw = 2 * (0.53 - 2) * 1 = -2.94
```
更新权重：
```
w = 0.53 - 0.01 * (-2.94) = 0.56
```

迭代 3: