## Derivative of CTC Loss
关于CTC的介绍已经有很多不错的教程了,但是完整的描述CTCLoss的前向和反向过程的很少,而且有些公式推导省略和错误。本文主要关注CTC Loss的梯度是如何计算的,关于CTC的介绍这里不做过多赘述,具体参看文末参考。
CTC主要应用于语音和OCR中,已语音[Deepspeech2](https://arxiv.org/abs/1512.02595)模型为例,CTC的网络一般如下图所示,包含softmax和CTCLoss两部分。反向传播需要求得loss L相对于logits $u^i$的梯度。下面先介绍CTCLoss的前向计算。
> 图片来源于文末参考

## 1. CTC Loss 的计算
CTC中path的定义与概率的计算如下:
 path 是 $ L'^T$的元素,用 $ \pi $表示。 $ \textbf{x} $ 是输入特征,$\textbf{y}$ 是输出label, 都是序列。 $ L $ 是输出的 vocab, L‘ 是 $ L \cup {blank}$。 $y_{\pi_{t}}^t$ 表示在t时刻,$\pi_{t}$ label时的观察概率。其中$\pi_{t}$ 表示 $\pi$ path在t时刻的label。$\pi$ 是 $\textbf{y}$ 与 $ \textbf{x}$ 的一个alignment,长度是$T$,取值空间为$L'$。path也称为alignment。
公式(2)解释了给定输入 $\textbf{x}$ ,输出 $ \pi $ path 的概率,即从时间t=1到T每个时间点的概率 $y_{\pi_{t}}^t$ 相乘。
求出单条path后,就可以计算$p(l \mid x)$ 的概率,计算如下:
path 是 $ L'^T$的元素,用 $ \pi $表示。 $ \textbf{x} $ 是输入特征,$\textbf{y}$ 是输出label, 都是序列。 $ L $ 是输出的 vocab, L‘ 是 $ L \cup {blank}$。 $y_{\pi_{t}}^t$ 表示在t时刻,$\pi_{t}$ label时的观察概率。其中$\pi_{t}$ 表示 $\pi$ path在t时刻的label。$\pi$ 是 $\textbf{y}$ 与 $ \textbf{x}$ 的一个alignment,长度是$T$,取值空间为$L'$。path也称为alignment。
公式(2)解释了给定输入 $\textbf{x}$ ,输出 $ \pi $ path 的概率,即从时间t=1到T每个时间点的概率 $y_{\pi_{t}}^t$ 相乘。
求出单条path后,就可以计算$p(l \mid x)$ 的概率,计算如下:
 这里边 $\mathcal{B}$ 就是映射, 即所有多对一的映射(many-to-one mapping )的集合。 这样就算出来对应一个真正的 label $\textbf{l}$ 的概率了,这里是求和。 求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。
公式(3)解释了给定输入 $\mathbf{x}$ ,求输出$\mathbf{l}$ 的概率, 即所有集合 $\mathcal{B}^{-1} (\mathbf{l})$ 中 path的概率和。
### 1.1 CTC forward-backward 算法
CTC的优化采用算最大似然估计[MLE (maximum likelihood estimation)](https://en.wikipedia.org/wiki/Maximum_likelihood_estimation), 这个和神经网络本身的训练过程是一致的。
这个CTC 计算过程类似HMM的 [forward-backward algorithm](https://en.wikipedia.org/wiki/Forward%E2%80%93backward_algorithm),下面就是这个算法的推导过程:
这里边 $\mathcal{B}$ 就是映射, 即所有多对一的映射(many-to-one mapping )的集合。 这样就算出来对应一个真正的 label $\textbf{l}$ 的概率了,这里是求和。 求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。
公式(3)解释了给定输入 $\mathbf{x}$ ,求输出$\mathbf{l}$ 的概率, 即所有集合 $\mathcal{B}^{-1} (\mathbf{l})$ 中 path的概率和。
### 1.1 CTC forward-backward 算法
CTC的优化采用算最大似然估计[MLE (maximum likelihood estimation)](https://en.wikipedia.org/wiki/Maximum_likelihood_estimation), 这个和神经网络本身的训练过程是一致的。
这个CTC 计算过程类似HMM的 [forward-backward algorithm](https://en.wikipedia.org/wiki/Forward%E2%80%93backward_algorithm),下面就是这个算法的推导过程:
 上图中的定义很清楚, 但是$ \alpha_{t-1}(s) $ and $ \alpha_{t-1}(s-1)$ 和 $\alpha_t(s)$ 的关系也不那么好看出来,下图给出了具体的关于 $\alpha_t(s)$ 的推导过程:
上图中的定义很清楚, 但是$ \alpha_{t-1}(s) $ and $ \alpha_{t-1}(s-1)$ 和 $\alpha_t(s)$ 的关系也不那么好看出来,下图给出了具体的关于 $\alpha_t(s)$ 的推导过程:

 这里的公式比较适合用下面的图来理解,$\alpha_1(1)$ 其实对应的就是下图中左上角白色的圆圈。 就是上来第一个是blank 的概率, 而 $\alpha_1(2)$是label l 的第一个字母。 这里边我们假设每个字母之间都插入了空白,即label l扩展成l',例如,l=[a, b, b, c], l'=[-, a, -, b, -, b, -, c, -]。 然后对于其他圆点,在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t,从左到右是1到T;纵轴是s(sequence),从上到下是 1 到 $\mathbf{\mid l' \mid}$.
这里的公式比较适合用下面的图来理解,$\alpha_1(1)$ 其实对应的就是下图中左上角白色的圆圈。 就是上来第一个是blank 的概率, 而 $\alpha_1(2)$是label l 的第一个字母。 这里边我们假设每个字母之间都插入了空白,即label l扩展成l',例如,l=[a, b, b, c], l'=[-, a, -, b, -, b, -, c, -]。 然后对于其他圆点,在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t,从左到右是1到T;纵轴是s(sequence),从上到下是 1 到 $\mathbf{\mid l' \mid}$.
 接下来我们分析递归公式 (resursion),更多介绍可以参看 [2]. 公式6分情况考虑:
* 第一种情况就是当前的label是blank, 或者 $\mathbf{l'}_{s}= \mathbf{l'}_{s-2}$(相邻是重复字符):

这个时候他的概率来自于过去t-1的两个label 概率, 也就是 $a_{t-1} (s)$ 和 $a_{t-1} (s-1)$ 。
$ a_{t-1} (s)$ 就是说当前的 sequence 已经是s 了,figure 3中表现为横跳, blank -->blank(例如t=3, s=3);
而 $a_{t-1} (s-1) $是说明当前的字符还不够, 需要再加一个, 所以在figure 3中就是斜跳,从黑色圆圈到白色圆圈(例如,t=3, s=5)。
仔细观察figure 3, 除了第一排的白色圆圈, 其他白色圆圈都有两个输入, 就是上述的两种情况。 当然判断blank 的方法也可以是判断$I'_{s-2} = I'_{s}$. 这种情况也是说明$I'_{s}$ 是blank, 因为每一个字符必须用 blank 隔开, 即使是相同字符。
* 第二章情况 也可以用类似逻辑得出, 只不过当前的状态s 是黑色圆圈, 有三种情况输入。

最终的概率就如公式8 所示, 这个计算过程就是 CTC forward algroirthm, 基于 Fig. 3 的左边的初始条件。
接下来我们分析递归公式 (resursion),更多介绍可以参看 [2]. 公式6分情况考虑:
* 第一种情况就是当前的label是blank, 或者 $\mathbf{l'}_{s}= \mathbf{l'}_{s-2}$(相邻是重复字符):

这个时候他的概率来自于过去t-1的两个label 概率, 也就是 $a_{t-1} (s)$ 和 $a_{t-1} (s-1)$ 。
$ a_{t-1} (s)$ 就是说当前的 sequence 已经是s 了,figure 3中表现为横跳, blank -->blank(例如t=3, s=3);
而 $a_{t-1} (s-1) $是说明当前的字符还不够, 需要再加一个, 所以在figure 3中就是斜跳,从黑色圆圈到白色圆圈(例如,t=3, s=5)。
仔细观察figure 3, 除了第一排的白色圆圈, 其他白色圆圈都有两个输入, 就是上述的两种情况。 当然判断blank 的方法也可以是判断$I'_{s-2} = I'_{s}$. 这种情况也是说明$I'_{s}$ 是blank, 因为每一个字符必须用 blank 隔开, 即使是相同字符。
* 第二章情况 也可以用类似逻辑得出, 只不过当前的状态s 是黑色圆圈, 有三种情况输入。

最终的概率就如公式8 所示, 这个计算过程就是 CTC forward algroirthm, 基于 Fig. 3 的左边的初始条件。
 基于Fig. 3 右边的初始条件,我们还是可以计算出一个概率, 那个就是 **CTC backward**. 这里我就不详细介绍了, 直接截图。
基于Fig. 3 右边的初始条件,我们还是可以计算出一个概率, 那个就是 **CTC backward**. 这里我就不详细介绍了, 直接截图。
 这样一直做乘法, 数字值越来越小,很快就会underflow。 这个时候就需要做 scaling.
这样一直做乘法, 数字值越来越小,很快就会underflow。 这个时候就需要做 scaling.
 算出了forward probability 和 backward probability 有什么用呢, 解释如下图。
算出了forward probability 和 backward probability 有什么用呢, 解释如下图。
 上图是说 forward probability and backward probability 的乘积, 代表了这个 sequence $\mathbf{l}$ t时刻,是s label 的 所有paths 的概率。 这样的话 我们就计算了 Fig. 3 中的每个圆圈的概率。为什么$\alpha_t(s)\beta_t(s)$ 中多出一个 $y^t_{\mathbf{l'_s}}$ ,这是因为它在 $\alpha$ 和 $\beta$ 中都包含该项,合并公式后就多出一项。
上图是说 forward probability and backward probability 的乘积, 代表了这个 sequence $\mathbf{l}$ t时刻,是s label 的 所有paths 的概率。 这样的话 我们就计算了 Fig. 3 中的每个圆圈的概率。为什么$\alpha_t(s)\beta_t(s)$ 中多出一个 $y^t_{\mathbf{l'_s}}$ ,这是因为它在 $\alpha$ 和 $\beta$ 中都包含该项,合并公式后就多出一项。
 $p(\mathbf{l}|\mathbf{x})$ 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL(Negative Log Likelihood)。
### 1.2 总结
总结一下,根据前向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,前向概率:
$$
\begin{split}
\alpha_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{1:t}|x) \newline
\alpha_1(1) &= y_{-}^1 ; \quad \alpha_1(2)=y^1_{l'_2}, \quad \alpha_1(s)=0, \forall s > 2 \newline
\alpha_t(s) &= 0, \quad \forall s < |l'| - 2(T-t) - 1 ,\quad \text{or} \quad \forall s < 1 \newline
\alpha_t(s) &=
\begin{cases}
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s-2} = l'_s$} \newline
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\alpha_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\alpha_{T}(|l'|)+\alpha_{T}(|l'|-1))
$$
根据后向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,后向概率:
$$
\begin{split}
\beta_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{t:T}|x) \newline
\beta_T(|l'|) &= y_{-}^T ; \quad \beta_T(|l'|-1)=y^T_{l'_{|l'|-1}}, \quad \beta_T(s)=0, \forall s < |l'| - 1 \newline
\beta_t(s) &= 0, \text{$\forall s > 2t$ or $\forall s < |l'|$} \newline
\beta_t(s) &=
\begin{cases}
(\beta_{t+1}(s) + \beta_{t+1}(s+1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s+2} = l'_s$} \newline
(\beta_{t+1}(s) + \beta_{t+1}(s+1) + \beta_{t+1}(s+2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\beta_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\beta_{1}(1)+\beta_{1}(2)) \newline
$$
根据任意时刻的前向概率和后向概率计算CTC Loss函数,得到如下结论:
1. 对于任意时刻t,利用前向概率和后向概率计算CTCLoss:
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \newline
-ln(p(l \mid x)) = -ln( \sum_{s=1}^{|l'|} \frac{\alpha_t(s) \beta_t(s)}{y_{l'_s}^t} )
$$
我们已经得到CTCLoss的计算方法,接下来对其进行求导。
## 2. CTC梯度计算
### 2.1 微分公式
在计算梯度前,我们先回顾下基本的微分公式:
$$
C' &= 0 \newline
x' &= 1 \newline
x^n &= n \cdot x^{n-1} \newline
(e^x)' &= e^x \newline
log(x)' &= \frac{1}{x} \newline
(u + v)' &= u' + v' \newline
(\frac{u}{v})' &= \frac{u'v-uv'}{v^2} \newline
\frac{\mathrm{d}f(g(x))}{\mathrm{d}x} &= \frac{\mathrm{d}f(g(x))}{\mathrm{d}g(x)} \cdot \frac{\mathrm{d}g(x)}{\mathrm{d}x}
$$
### 2.2 CTC梯度
最大似然估计训练就是最大化训练集中每一个分类的对数概率,即最小化Eq. 12。
$p(\mathbf{l}|\mathbf{x})$ 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL(Negative Log Likelihood)。
### 1.2 总结
总结一下,根据前向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,前向概率:
$$
\begin{split}
\alpha_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{1:t}|x) \newline
\alpha_1(1) &= y_{-}^1 ; \quad \alpha_1(2)=y^1_{l'_2}, \quad \alpha_1(s)=0, \forall s > 2 \newline
\alpha_t(s) &= 0, \quad \forall s < |l'| - 2(T-t) - 1 ,\quad \text{or} \quad \forall s < 1 \newline
\alpha_t(s) &=
\begin{cases}
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s-2} = l'_s$} \newline
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\alpha_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\alpha_{T}(|l'|)+\alpha_{T}(|l'|-1))
$$
根据后向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,后向概率:
$$
\begin{split}
\beta_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{t:T}|x) \newline
\beta_T(|l'|) &= y_{-}^T ; \quad \beta_T(|l'|-1)=y^T_{l'_{|l'|-1}}, \quad \beta_T(s)=0, \forall s < |l'| - 1 \newline
\beta_t(s) &= 0, \text{$\forall s > 2t$ or $\forall s < |l'|$} \newline
\beta_t(s) &=
\begin{cases}
(\beta_{t+1}(s) + \beta_{t+1}(s+1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s+2} = l'_s$} \newline
(\beta_{t+1}(s) + \beta_{t+1}(s+1) + \beta_{t+1}(s+2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\beta_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\beta_{1}(1)+\beta_{1}(2)) \newline
$$
根据任意时刻的前向概率和后向概率计算CTC Loss函数,得到如下结论:
1. 对于任意时刻t,利用前向概率和后向概率计算CTCLoss:
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \newline
-ln(p(l \mid x)) = -ln( \sum_{s=1}^{|l'|} \frac{\alpha_t(s) \beta_t(s)}{y_{l'_s}^t} )
$$
我们已经得到CTCLoss的计算方法,接下来对其进行求导。
## 2. CTC梯度计算
### 2.1 微分公式
在计算梯度前,我们先回顾下基本的微分公式:
$$
C' &= 0 \newline
x' &= 1 \newline
x^n &= n \cdot x^{n-1} \newline
(e^x)' &= e^x \newline
log(x)' &= \frac{1}{x} \newline
(u + v)' &= u' + v' \newline
(\frac{u}{v})' &= \frac{u'v-uv'}{v^2} \newline
\frac{\mathrm{d}f(g(x))}{\mathrm{d}x} &= \frac{\mathrm{d}f(g(x))}{\mathrm{d}g(x)} \cdot \frac{\mathrm{d}g(x)}{\mathrm{d}x}
$$
### 2.2 CTC梯度
最大似然估计训练就是最大化训练集中每一个分类的对数概率,即最小化Eq. 12。
 最后就是算微分了, 整个推导过程就是加法和乘法, 都可以微分。 $\mathit{O}^{ML}$关于神经网络的输出 $y^t_k$的梯度见Eq. 13。因为训练样本是相互独立的,所以可以单独考虑每个样本,公式如Eq.13。
下面是CTCLoss的梯度计算:
最后就是算微分了, 整个推导过程就是加法和乘法, 都可以微分。 $\mathit{O}^{ML}$关于神经网络的输出 $y^t_k$的梯度见Eq. 13。因为训练样本是相互独立的,所以可以单独考虑每个样本,公式如Eq.13。
下面是CTCLoss的梯度计算:
 ### 2.3 CTC梯度推导
回顾下之前的公式,便于理解后续推导过程。
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \\
\begin{equation}
\alpha_t(s) \beta_t(s) = \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(l):} } y^t_{l'_s} \prod_{t=1}^T y^t_{\pi_t}
\end{equation}
$$
其中Eq. 15的计算过程如下:
$$
\begin{align*}
\frac{\part p(
l \mid x)}{\part y_k^t}
& = \sum_{s \in lab(z,k)} \frac{ \part \frac{ \alpha_t(s) \beta_t(s)}{y_{k}^t}}{\part y_k^t}
\newline
& = \sum_{s \in lab(z,k)} \frac{(\alpha_t(s)\beta_t(s))’y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{( \prod_{t'=1}^{t-1} y^{t'}_{\pi_{t'}} \cdot y_k^t \cdot y_k^t \cdot \prod_{t'=t+1}^{T} y^{t'}_{\pi_{t'}} )’ y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{2\alpha_t(s)\beta_t(s) - \alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{\alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \frac{1}{{y_k^t}^2} \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \tag{1} \newline
\end{align*}
$$
NLL的公式推导如下:
$$
\begin{split}
\frac{\part {ln(p(l \mid x))} }{ \part y^t_k }
&= \frac{1}{p(l \mid x)} \frac{ \part{p(l \mid x)} }{ \part y_k^t } \newline
&= \frac{1}{p(l \mid x) {y^t_k}^2 } \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s)
\end{split}
\tag{2}
$$
已经算出了CTCLoss对于 $y_k^t$ 的梯度,接下来我们需要计算 CTCLoss对于$u^t_k$(logits)的梯度。套用链式法则,并替换$y^t_k$ 为 $y^t_{k'}$,结果如下图。图中 $k'$ 表示vocab中的某一个token,$K$ 是vocab的大小。
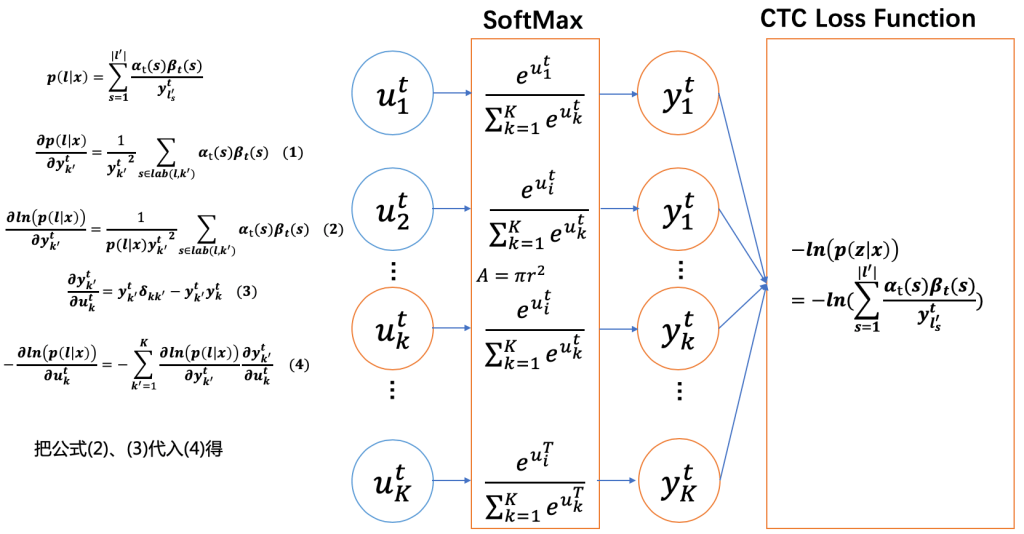
图中公式4根据链式法则得到:
$$
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
= - \sum_{k'=1}^{K} \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'} }{ \part u^t_k } \tag{4}
$$
图中公式3是softmax的梯度,参考 [4],计算过程如下:
$$
softmax(j) = S_j = \frac{ e^{a_j} }{ \sum_{k=1}^K e^{a_k} }, \enspace \forall j \in 1 \dots K
$$
$$
\begin{split}
\frac{ \part S_i }{ \part a_j}
&= \frac{ \part (\frac{ e^{ a_i } }{ \sum_k e^{ a_k } }) } { \part a_j }
\newline
&=
\begin{cases}
\frac{ e^a_i \sum - e^a_j e^a_i }{ \sum^2 }
&= \frac{ e^a_i }{ \sum } \frac{ \sum - e^a_j }{ \sum } \newline
&= S_i(1-S_j) & \text{i = j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\newline
\frac{ 0 - e^a_j e^a_i }{ \sum^2 }
&= - \frac{ e^a_j }{ \sum } \frac{ e^a_i }{ \sum } \newline
&= -S_j S_i & \text{i $\neq$ j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\end{cases}
\newline
&=
\begin{cases}
S_i(1 - S_j) & \text{$i = j$}
\newline
-S_j S_i = S_i (0 - S_j) & \text{$i \neq j$}
\end{cases}
\newline
&= S_i (\delta_{ij} - S_j )
\end{split}
\tag{3}
$$
$$
\delta_{ij} =
\begin{cases}
1 & \text{if i = j} \newline
0 & \text{otherwise}
\end{cases}
$$
下图中黄色框中的部分表示公式(1),即遍历所有的vocab中的token,其结果是$p(l \mid x)$。这是因为label $l$ 中的token一定在vocab中,且 $s \in lab(l, k')$ 可以是空集。当 $k'$ 在 l 中,s 则为label中token是$k'$的概率;当$k'$不在l中,s为空,概率为0。
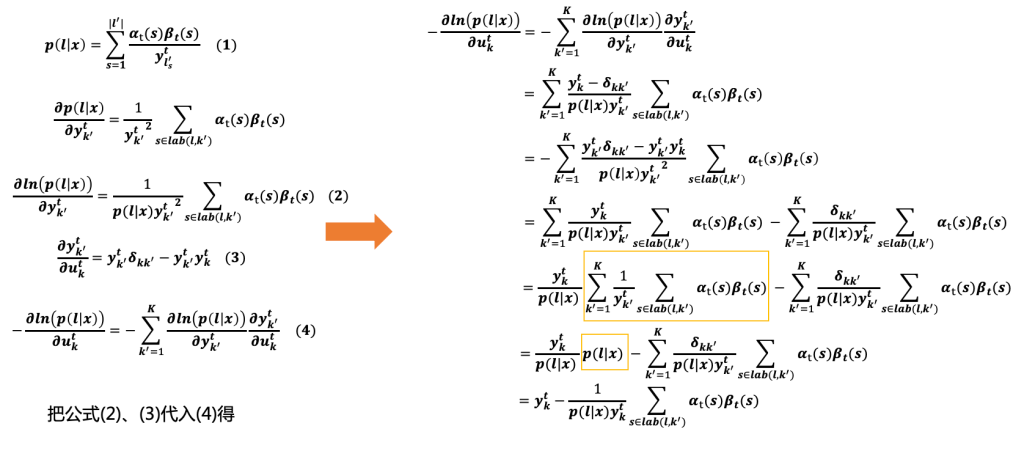
公式(2),(3)带入(4),并结合公式(1)的结果如上图右边,即:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &=
- \sum_{k'=1}^K \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'}}{ \part u^t_k } \newline
&= - \sum_{k'=1}^K \frac{ y^t_{k'}( \delta_{kk'} - y^t_k ) }{ p(l \mid x) {y^t_{k'}}^2 } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= - \sum_{k'=1}^K \frac{ \delta_{kk'} - y^t_k }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t_k - \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } ( \sum_{k'=1}^K \frac{1}{y^t_{k'}} \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) ) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } p(l \mid x) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline
\end{split}
$$
最终,为了通过softmax层传播CTCLoss的梯度,需要计算目标函数与 logits $u^t_k$的偏微分,即Eq. 16:
$$
\begin{align*}
\hat{\alpha}_t(s) & \overset{def}{=} \frac{ \alpha_t(s) }{ C_t } ,\enspace C_t \overset{def}{=} \sum_s \alpha_t(s)
\newline
\hat{\beta}_t(s) & \overset{def}{=} \frac{ \beta_t(s) }{ D_t } ,\enspace D_t \overset{def}{=} \sum_s \beta_t(s)
\newline
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \tag{16}
\newline
\end{align*}
$$
### 2.1 总结
* 通过动态规划算法计算$\alpha_t(s)$ 和 $\beta_t(s)$
* 通过$\alpha_t(s)$ 计算 $p(l \mid x)=\alpha_T(\mid l' \mid) + \alpha_T(\mid l' \mid -1)$
* 通过$\alpha_t(s)$ 和 $\beta_t(s)$ 计算CTcLoss函数的导数:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s)
\newline
&= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s)
\newline
\end{split}
\tag{16}
$$
## Reference
[[1] A. Graves, S. Fernandez, F. Gomez, J. Schmidhuber. Connectionist Temporal lassification: Labeling Unsegmented Sequence Data with Recurrent Neural Networks. ICML 2006, Pittsburgh, USA, pp. 369-376.](http://www.cs.toronto.edu/~graves/icml_2006.pdf)
[[2] Sequence ModelingWith CTC](https://distill.pub/2017/ctc/)
[[3] NLP 之 CTC Loss 的工作原理](https://www.jianshu.com/p/e073c9d91b20)
[[4] The Softmax function and its derivative](https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/)
[[5] CTC Algorithm Explained Part 1:Training the Network(CTC算法详解之训练篇)](https://xiaodu.io/ctc-explained/)
### 2.3 CTC梯度推导
回顾下之前的公式,便于理解后续推导过程。
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \\
\begin{equation}
\alpha_t(s) \beta_t(s) = \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(l):} } y^t_{l'_s} \prod_{t=1}^T y^t_{\pi_t}
\end{equation}
$$
其中Eq. 15的计算过程如下:
$$
\begin{align*}
\frac{\part p(
l \mid x)}{\part y_k^t}
& = \sum_{s \in lab(z,k)} \frac{ \part \frac{ \alpha_t(s) \beta_t(s)}{y_{k}^t}}{\part y_k^t}
\newline
& = \sum_{s \in lab(z,k)} \frac{(\alpha_t(s)\beta_t(s))’y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{( \prod_{t'=1}^{t-1} y^{t'}_{\pi_{t'}} \cdot y_k^t \cdot y_k^t \cdot \prod_{t'=t+1}^{T} y^{t'}_{\pi_{t'}} )’ y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{2\alpha_t(s)\beta_t(s) - \alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{\alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \frac{1}{{y_k^t}^2} \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \tag{1} \newline
\end{align*}
$$
NLL的公式推导如下:
$$
\begin{split}
\frac{\part {ln(p(l \mid x))} }{ \part y^t_k }
&= \frac{1}{p(l \mid x)} \frac{ \part{p(l \mid x)} }{ \part y_k^t } \newline
&= \frac{1}{p(l \mid x) {y^t_k}^2 } \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s)
\end{split}
\tag{2}
$$
已经算出了CTCLoss对于 $y_k^t$ 的梯度,接下来我们需要计算 CTCLoss对于$u^t_k$(logits)的梯度。套用链式法则,并替换$y^t_k$ 为 $y^t_{k'}$,结果如下图。图中 $k'$ 表示vocab中的某一个token,$K$ 是vocab的大小。

图中公式4根据链式法则得到:
$$
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
= - \sum_{k'=1}^{K} \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'} }{ \part u^t_k } \tag{4}
$$
图中公式3是softmax的梯度,参考 [4],计算过程如下:
$$
softmax(j) = S_j = \frac{ e^{a_j} }{ \sum_{k=1}^K e^{a_k} }, \enspace \forall j \in 1 \dots K
$$
$$
\begin{split}
\frac{ \part S_i }{ \part a_j}
&= \frac{ \part (\frac{ e^{ a_i } }{ \sum_k e^{ a_k } }) } { \part a_j }
\newline
&=
\begin{cases}
\frac{ e^a_i \sum - e^a_j e^a_i }{ \sum^2 }
&= \frac{ e^a_i }{ \sum } \frac{ \sum - e^a_j }{ \sum } \newline
&= S_i(1-S_j) & \text{i = j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\newline
\frac{ 0 - e^a_j e^a_i }{ \sum^2 }
&= - \frac{ e^a_j }{ \sum } \frac{ e^a_i }{ \sum } \newline
&= -S_j S_i & \text{i $\neq$ j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\end{cases}
\newline
&=
\begin{cases}
S_i(1 - S_j) & \text{$i = j$}
\newline
-S_j S_i = S_i (0 - S_j) & \text{$i \neq j$}
\end{cases}
\newline
&= S_i (\delta_{ij} - S_j )
\end{split}
\tag{3}
$$
$$
\delta_{ij} =
\begin{cases}
1 & \text{if i = j} \newline
0 & \text{otherwise}
\end{cases}
$$
下图中黄色框中的部分表示公式(1),即遍历所有的vocab中的token,其结果是$p(l \mid x)$。这是因为label $l$ 中的token一定在vocab中,且 $s \in lab(l, k')$ 可以是空集。当 $k'$ 在 l 中,s 则为label中token是$k'$的概率;当$k'$不在l中,s为空,概率为0。

公式(2),(3)带入(4),并结合公式(1)的结果如上图右边,即:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &=
- \sum_{k'=1}^K \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'}}{ \part u^t_k } \newline
&= - \sum_{k'=1}^K \frac{ y^t_{k'}( \delta_{kk'} - y^t_k ) }{ p(l \mid x) {y^t_{k'}}^2 } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= - \sum_{k'=1}^K \frac{ \delta_{kk'} - y^t_k }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t_k - \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } ( \sum_{k'=1}^K \frac{1}{y^t_{k'}} \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) ) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } p(l \mid x) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline
\end{split}
$$
最终,为了通过softmax层传播CTCLoss的梯度,需要计算目标函数与 logits $u^t_k$的偏微分,即Eq. 16:
$$
\begin{align*}
\hat{\alpha}_t(s) & \overset{def}{=} \frac{ \alpha_t(s) }{ C_t } ,\enspace C_t \overset{def}{=} \sum_s \alpha_t(s)
\newline
\hat{\beta}_t(s) & \overset{def}{=} \frac{ \beta_t(s) }{ D_t } ,\enspace D_t \overset{def}{=} \sum_s \beta_t(s)
\newline
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \tag{16}
\newline
\end{align*}
$$
### 2.1 总结
* 通过动态规划算法计算$\alpha_t(s)$ 和 $\beta_t(s)$
* 通过$\alpha_t(s)$ 计算 $p(l \mid x)=\alpha_T(\mid l' \mid) + \alpha_T(\mid l' \mid -1)$
* 通过$\alpha_t(s)$ 和 $\beta_t(s)$ 计算CTcLoss函数的导数:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s)
\newline
&= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s)
\newline
\end{split}
\tag{16}
$$
## Reference
[[1] A. Graves, S. Fernandez, F. Gomez, J. Schmidhuber. Connectionist Temporal lassification: Labeling Unsegmented Sequence Data with Recurrent Neural Networks. ICML 2006, Pittsburgh, USA, pp. 369-376.](http://www.cs.toronto.edu/~graves/icml_2006.pdf)
[[2] Sequence ModelingWith CTC](https://distill.pub/2017/ctc/)
[[3] NLP 之 CTC Loss 的工作原理](https://www.jianshu.com/p/e073c9d91b20)
[[4] The Softmax function and its derivative](https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/)
[[5] CTC Algorithm Explained Part 1:Training the Network(CTC算法详解之训练篇)](https://xiaodu.io/ctc-explained/)
 path 是 $ L'^T$的元素,用 $ \pi $表示。 $ \textbf{x} $ 是输入特征,$\textbf{y}$ 是输出label, 都是序列。 $ L $ 是输出的 vocab, L‘ 是 $ L \cup {blank}$。 $y_{\pi_{t}}^t$ 表示在t时刻,$\pi_{t}$ label时的观察概率。其中$\pi_{t}$ 表示 $\pi$ path在t时刻的label。$\pi$ 是 $\textbf{y}$ 与 $ \textbf{x}$ 的一个alignment,长度是$T$,取值空间为$L'$。path也称为alignment。
公式(2)解释了给定输入 $\textbf{x}$ ,输出 $ \pi $ path 的概率,即从时间t=1到T每个时间点的概率 $y_{\pi_{t}}^t$ 相乘。
求出单条path后,就可以计算$p(l \mid x)$ 的概率,计算如下:
path 是 $ L'^T$的元素,用 $ \pi $表示。 $ \textbf{x} $ 是输入特征,$\textbf{y}$ 是输出label, 都是序列。 $ L $ 是输出的 vocab, L‘ 是 $ L \cup {blank}$。 $y_{\pi_{t}}^t$ 表示在t时刻,$\pi_{t}$ label时的观察概率。其中$\pi_{t}$ 表示 $\pi$ path在t时刻的label。$\pi$ 是 $\textbf{y}$ 与 $ \textbf{x}$ 的一个alignment,长度是$T$,取值空间为$L'$。path也称为alignment。
公式(2)解释了给定输入 $\textbf{x}$ ,输出 $ \pi $ path 的概率,即从时间t=1到T每个时间点的概率 $y_{\pi_{t}}^t$ 相乘。
求出单条path后,就可以计算$p(l \mid x)$ 的概率,计算如下:
 这里边 $\mathcal{B}$ 就是映射, 即所有多对一的映射(many-to-one mapping )的集合。 这样就算出来对应一个真正的 label $\textbf{l}$ 的概率了,这里是求和。 求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。
公式(3)解释了给定输入 $\mathbf{x}$ ,求输出$\mathbf{l}$ 的概率, 即所有集合 $\mathcal{B}^{-1} (\mathbf{l})$ 中 path的概率和。
### 1.1 CTC forward-backward 算法
CTC的优化采用算最大似然估计[MLE (maximum likelihood estimation)](https://en.wikipedia.org/wiki/Maximum_likelihood_estimation), 这个和神经网络本身的训练过程是一致的。
这个CTC 计算过程类似HMM的 [forward-backward algorithm](https://en.wikipedia.org/wiki/Forward%E2%80%93backward_algorithm),下面就是这个算法的推导过程:
这里边 $\mathcal{B}$ 就是映射, 即所有多对一的映射(many-to-one mapping )的集合。 这样就算出来对应一个真正的 label $\textbf{l}$ 的概率了,这里是求和。 求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。
公式(3)解释了给定输入 $\mathbf{x}$ ,求输出$\mathbf{l}$ 的概率, 即所有集合 $\mathcal{B}^{-1} (\mathbf{l})$ 中 path的概率和。
### 1.1 CTC forward-backward 算法
CTC的优化采用算最大似然估计[MLE (maximum likelihood estimation)](https://en.wikipedia.org/wiki/Maximum_likelihood_estimation), 这个和神经网络本身的训练过程是一致的。
这个CTC 计算过程类似HMM的 [forward-backward algorithm](https://en.wikipedia.org/wiki/Forward%E2%80%93backward_algorithm),下面就是这个算法的推导过程:
 上图中的定义很清楚, 但是$ \alpha_{t-1}(s) $ and $ \alpha_{t-1}(s-1)$ 和 $\alpha_t(s)$ 的关系也不那么好看出来,下图给出了具体的关于 $\alpha_t(s)$ 的推导过程:
上图中的定义很清楚, 但是$ \alpha_{t-1}(s) $ and $ \alpha_{t-1}(s-1)$ 和 $\alpha_t(s)$ 的关系也不那么好看出来,下图给出了具体的关于 $\alpha_t(s)$ 的推导过程:

 这里的公式比较适合用下面的图来理解,$\alpha_1(1)$ 其实对应的就是下图中左上角白色的圆圈。 就是上来第一个是blank 的概率, 而 $\alpha_1(2)$是label l 的第一个字母。 这里边我们假设每个字母之间都插入了空白,即label l扩展成l',例如,l=[a, b, b, c], l'=[-, a, -, b, -, b, -, c, -]。 然后对于其他圆点,在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t,从左到右是1到T;纵轴是s(sequence),从上到下是 1 到 $\mathbf{\mid l' \mid}$.
这里的公式比较适合用下面的图来理解,$\alpha_1(1)$ 其实对应的就是下图中左上角白色的圆圈。 就是上来第一个是blank 的概率, 而 $\alpha_1(2)$是label l 的第一个字母。 这里边我们假设每个字母之间都插入了空白,即label l扩展成l',例如,l=[a, b, b, c], l'=[-, a, -, b, -, b, -, c, -]。 然后对于其他圆点,在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t,从左到右是1到T;纵轴是s(sequence),从上到下是 1 到 $\mathbf{\mid l' \mid}$.
 接下来我们分析递归公式 (resursion),更多介绍可以参看 [2]. 公式6分情况考虑:
* 第一种情况就是当前的label是blank, 或者 $\mathbf{l'}_{s}= \mathbf{l'}_{s-2}$(相邻是重复字符):

这个时候他的概率来自于过去t-1的两个label 概率, 也就是 $a_{t-1} (s)$ 和 $a_{t-1} (s-1)$ 。
$ a_{t-1} (s)$ 就是说当前的 sequence 已经是s 了,figure 3中表现为横跳, blank -->blank(例如t=3, s=3);
而 $a_{t-1} (s-1) $是说明当前的字符还不够, 需要再加一个, 所以在figure 3中就是斜跳,从黑色圆圈到白色圆圈(例如,t=3, s=5)。
仔细观察figure 3, 除了第一排的白色圆圈, 其他白色圆圈都有两个输入, 就是上述的两种情况。 当然判断blank 的方法也可以是判断$I'_{s-2} = I'_{s}$. 这种情况也是说明$I'_{s}$ 是blank, 因为每一个字符必须用 blank 隔开, 即使是相同字符。
* 第二章情况 也可以用类似逻辑得出, 只不过当前的状态s 是黑色圆圈, 有三种情况输入。

最终的概率就如公式8 所示, 这个计算过程就是 CTC forward algroirthm, 基于 Fig. 3 的左边的初始条件。
接下来我们分析递归公式 (resursion),更多介绍可以参看 [2]. 公式6分情况考虑:
* 第一种情况就是当前的label是blank, 或者 $\mathbf{l'}_{s}= \mathbf{l'}_{s-2}$(相邻是重复字符):

这个时候他的概率来自于过去t-1的两个label 概率, 也就是 $a_{t-1} (s)$ 和 $a_{t-1} (s-1)$ 。
$ a_{t-1} (s)$ 就是说当前的 sequence 已经是s 了,figure 3中表现为横跳, blank -->blank(例如t=3, s=3);
而 $a_{t-1} (s-1) $是说明当前的字符还不够, 需要再加一个, 所以在figure 3中就是斜跳,从黑色圆圈到白色圆圈(例如,t=3, s=5)。
仔细观察figure 3, 除了第一排的白色圆圈, 其他白色圆圈都有两个输入, 就是上述的两种情况。 当然判断blank 的方法也可以是判断$I'_{s-2} = I'_{s}$. 这种情况也是说明$I'_{s}$ 是blank, 因为每一个字符必须用 blank 隔开, 即使是相同字符。
* 第二章情况 也可以用类似逻辑得出, 只不过当前的状态s 是黑色圆圈, 有三种情况输入。

最终的概率就如公式8 所示, 这个计算过程就是 CTC forward algroirthm, 基于 Fig. 3 的左边的初始条件。
 基于Fig. 3 右边的初始条件,我们还是可以计算出一个概率, 那个就是 **CTC backward**. 这里我就不详细介绍了, 直接截图。
基于Fig. 3 右边的初始条件,我们还是可以计算出一个概率, 那个就是 **CTC backward**. 这里我就不详细介绍了, 直接截图。
 这样一直做乘法, 数字值越来越小,很快就会underflow。 这个时候就需要做 scaling.
这样一直做乘法, 数字值越来越小,很快就会underflow。 这个时候就需要做 scaling.
 算出了forward probability 和 backward probability 有什么用呢, 解释如下图。
算出了forward probability 和 backward probability 有什么用呢, 解释如下图。
 上图是说 forward probability and backward probability 的乘积, 代表了这个 sequence $\mathbf{l}$ t时刻,是s label 的 所有paths 的概率。 这样的话 我们就计算了 Fig. 3 中的每个圆圈的概率。为什么$\alpha_t(s)\beta_t(s)$ 中多出一个 $y^t_{\mathbf{l'_s}}$ ,这是因为它在 $\alpha$ 和 $\beta$ 中都包含该项,合并公式后就多出一项。
上图是说 forward probability and backward probability 的乘积, 代表了这个 sequence $\mathbf{l}$ t时刻,是s label 的 所有paths 的概率。 这样的话 我们就计算了 Fig. 3 中的每个圆圈的概率。为什么$\alpha_t(s)\beta_t(s)$ 中多出一个 $y^t_{\mathbf{l'_s}}$ ,这是因为它在 $\alpha$ 和 $\beta$ 中都包含该项,合并公式后就多出一项。
 $p(\mathbf{l}|\mathbf{x})$ 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL(Negative Log Likelihood)。
### 1.2 总结
总结一下,根据前向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,前向概率:
$$
\begin{split}
\alpha_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{1:t}|x) \newline
\alpha_1(1) &= y_{-}^1 ; \quad \alpha_1(2)=y^1_{l'_2}, \quad \alpha_1(s)=0, \forall s > 2 \newline
\alpha_t(s) &= 0, \quad \forall s < |l'| - 2(T-t) - 1 ,\quad \text{or} \quad \forall s < 1 \newline
\alpha_t(s) &=
\begin{cases}
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s-2} = l'_s$} \newline
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\alpha_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\alpha_{T}(|l'|)+\alpha_{T}(|l'|-1))
$$
根据后向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,后向概率:
$$
\begin{split}
\beta_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{t:T}|x) \newline
\beta_T(|l'|) &= y_{-}^T ; \quad \beta_T(|l'|-1)=y^T_{l'_{|l'|-1}}, \quad \beta_T(s)=0, \forall s < |l'| - 1 \newline
\beta_t(s) &= 0, \text{$\forall s > 2t$ or $\forall s < |l'|$} \newline
\beta_t(s) &=
\begin{cases}
(\beta_{t+1}(s) + \beta_{t+1}(s+1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s+2} = l'_s$} \newline
(\beta_{t+1}(s) + \beta_{t+1}(s+1) + \beta_{t+1}(s+2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\beta_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\beta_{1}(1)+\beta_{1}(2)) \newline
$$
根据任意时刻的前向概率和后向概率计算CTC Loss函数,得到如下结论:
1. 对于任意时刻t,利用前向概率和后向概率计算CTCLoss:
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \newline
-ln(p(l \mid x)) = -ln( \sum_{s=1}^{|l'|} \frac{\alpha_t(s) \beta_t(s)}{y_{l'_s}^t} )
$$
我们已经得到CTCLoss的计算方法,接下来对其进行求导。
## 2. CTC梯度计算
### 2.1 微分公式
在计算梯度前,我们先回顾下基本的微分公式:
$$
C' &= 0 \newline
x' &= 1 \newline
x^n &= n \cdot x^{n-1} \newline
(e^x)' &= e^x \newline
log(x)' &= \frac{1}{x} \newline
(u + v)' &= u' + v' \newline
(\frac{u}{v})' &= \frac{u'v-uv'}{v^2} \newline
\frac{\mathrm{d}f(g(x))}{\mathrm{d}x} &= \frac{\mathrm{d}f(g(x))}{\mathrm{d}g(x)} \cdot \frac{\mathrm{d}g(x)}{\mathrm{d}x}
$$
### 2.2 CTC梯度
最大似然估计训练就是最大化训练集中每一个分类的对数概率,即最小化Eq. 12。
$p(\mathbf{l}|\mathbf{x})$ 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL(Negative Log Likelihood)。
### 1.2 总结
总结一下,根据前向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,前向概率:
$$
\begin{split}
\alpha_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{1:t}|x) \newline
\alpha_1(1) &= y_{-}^1 ; \quad \alpha_1(2)=y^1_{l'_2}, \quad \alpha_1(s)=0, \forall s > 2 \newline
\alpha_t(s) &= 0, \quad \forall s < |l'| - 2(T-t) - 1 ,\quad \text{or} \quad \forall s < 1 \newline
\alpha_t(s) &=
\begin{cases}
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s-2} = l'_s$} \newline
(\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\alpha_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\alpha_{T}(|l'|)+\alpha_{T}(|l'|-1))
$$
根据后向概率计算CTCLoss函数,可以得出如下结论:
1. 对于时序长度为T的输入序列x和输出序列z,后向概率:
$$
\begin{split}
\beta_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{t:T}|x) \newline
\beta_T(|l'|) &= y_{-}^T ; \quad \beta_T(|l'|-1)=y^T_{l'_{|l'|-1}}, \quad \beta_T(s)=0, \forall s < |l'| - 1 \newline
\beta_t(s) &= 0, \text{$\forall s > 2t$ or $\forall s < |l'|$} \newline
\beta_t(s) &=
\begin{cases}
(\beta_{t+1}(s) + \beta_{t+1}(s+1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s+2} = l'_s$} \newline
(\beta_{t+1}(s) + \beta_{t+1}(s+1) + \beta_{t+1}(s+2))y^t_{l'_s} & \text{otherwise}\newline
\end{cases}
\end{split}
$$
2. 利用 $\beta_t(s)$计算CTCLoss:
$$
-ln(p(l \mid x)) = -ln(\beta_{1}(1)+\beta_{1}(2)) \newline
$$
根据任意时刻的前向概率和后向概率计算CTC Loss函数,得到如下结论:
1. 对于任意时刻t,利用前向概率和后向概率计算CTCLoss:
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \newline
-ln(p(l \mid x)) = -ln( \sum_{s=1}^{|l'|} \frac{\alpha_t(s) \beta_t(s)}{y_{l'_s}^t} )
$$
我们已经得到CTCLoss的计算方法,接下来对其进行求导。
## 2. CTC梯度计算
### 2.1 微分公式
在计算梯度前,我们先回顾下基本的微分公式:
$$
C' &= 0 \newline
x' &= 1 \newline
x^n &= n \cdot x^{n-1} \newline
(e^x)' &= e^x \newline
log(x)' &= \frac{1}{x} \newline
(u + v)' &= u' + v' \newline
(\frac{u}{v})' &= \frac{u'v-uv'}{v^2} \newline
\frac{\mathrm{d}f(g(x))}{\mathrm{d}x} &= \frac{\mathrm{d}f(g(x))}{\mathrm{d}g(x)} \cdot \frac{\mathrm{d}g(x)}{\mathrm{d}x}
$$
### 2.2 CTC梯度
最大似然估计训练就是最大化训练集中每一个分类的对数概率,即最小化Eq. 12。
 最后就是算微分了, 整个推导过程就是加法和乘法, 都可以微分。 $\mathit{O}^{ML}$关于神经网络的输出 $y^t_k$的梯度见Eq. 13。因为训练样本是相互独立的,所以可以单独考虑每个样本,公式如Eq.13。
下面是CTCLoss的梯度计算:
最后就是算微分了, 整个推导过程就是加法和乘法, 都可以微分。 $\mathit{O}^{ML}$关于神经网络的输出 $y^t_k$的梯度见Eq. 13。因为训练样本是相互独立的,所以可以单独考虑每个样本,公式如Eq.13。
下面是CTCLoss的梯度计算:
 ### 2.3 CTC梯度推导
回顾下之前的公式,便于理解后续推导过程。
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \\
\begin{equation}
\alpha_t(s) \beta_t(s) = \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(l):} } y^t_{l'_s} \prod_{t=1}^T y^t_{\pi_t}
\end{equation}
$$
其中Eq. 15的计算过程如下:
$$
\begin{align*}
\frac{\part p(
l \mid x)}{\part y_k^t}
& = \sum_{s \in lab(z,k)} \frac{ \part \frac{ \alpha_t(s) \beta_t(s)}{y_{k}^t}}{\part y_k^t}
\newline
& = \sum_{s \in lab(z,k)} \frac{(\alpha_t(s)\beta_t(s))’y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{( \prod_{t'=1}^{t-1} y^{t'}_{\pi_{t'}} \cdot y_k^t \cdot y_k^t \cdot \prod_{t'=t+1}^{T} y^{t'}_{\pi_{t'}} )’ y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{2\alpha_t(s)\beta_t(s) - \alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{\alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \frac{1}{{y_k^t}^2} \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \tag{1} \newline
\end{align*}
$$
NLL的公式推导如下:
$$
\begin{split}
\frac{\part {ln(p(l \mid x))} }{ \part y^t_k }
&= \frac{1}{p(l \mid x)} \frac{ \part{p(l \mid x)} }{ \part y_k^t } \newline
&= \frac{1}{p(l \mid x) {y^t_k}^2 } \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s)
\end{split}
\tag{2}
$$
已经算出了CTCLoss对于 $y_k^t$ 的梯度,接下来我们需要计算 CTCLoss对于$u^t_k$(logits)的梯度。套用链式法则,并替换$y^t_k$ 为 $y^t_{k'}$,结果如下图。图中 $k'$ 表示vocab中的某一个token,$K$ 是vocab的大小。

图中公式4根据链式法则得到:
$$
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
= - \sum_{k'=1}^{K} \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'} }{ \part u^t_k } \tag{4}
$$
图中公式3是softmax的梯度,参考 [4],计算过程如下:
$$
softmax(j) = S_j = \frac{ e^{a_j} }{ \sum_{k=1}^K e^{a_k} }, \enspace \forall j \in 1 \dots K
$$
$$
\begin{split}
\frac{ \part S_i }{ \part a_j}
&= \frac{ \part (\frac{ e^{ a_i } }{ \sum_k e^{ a_k } }) } { \part a_j }
\newline
&=
\begin{cases}
\frac{ e^a_i \sum - e^a_j e^a_i }{ \sum^2 }
&= \frac{ e^a_i }{ \sum } \frac{ \sum - e^a_j }{ \sum } \newline
&= S_i(1-S_j) & \text{i = j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\newline
\frac{ 0 - e^a_j e^a_i }{ \sum^2 }
&= - \frac{ e^a_j }{ \sum } \frac{ e^a_i }{ \sum } \newline
&= -S_j S_i & \text{i $\neq$ j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\end{cases}
\newline
&=
\begin{cases}
S_i(1 - S_j) & \text{$i = j$}
\newline
-S_j S_i = S_i (0 - S_j) & \text{$i \neq j$}
\end{cases}
\newline
&= S_i (\delta_{ij} - S_j )
\end{split}
\tag{3}
$$
$$
\delta_{ij} =
\begin{cases}
1 & \text{if i = j} \newline
0 & \text{otherwise}
\end{cases}
$$
下图中黄色框中的部分表示公式(1),即遍历所有的vocab中的token,其结果是$p(l \mid x)$。这是因为label $l$ 中的token一定在vocab中,且 $s \in lab(l, k')$ 可以是空集。当 $k'$ 在 l 中,s 则为label中token是$k'$的概率;当$k'$不在l中,s为空,概率为0。

公式(2),(3)带入(4),并结合公式(1)的结果如上图右边,即:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &=
- \sum_{k'=1}^K \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'}}{ \part u^t_k } \newline
&= - \sum_{k'=1}^K \frac{ y^t_{k'}( \delta_{kk'} - y^t_k ) }{ p(l \mid x) {y^t_{k'}}^2 } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= - \sum_{k'=1}^K \frac{ \delta_{kk'} - y^t_k }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t_k - \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } ( \sum_{k'=1}^K \frac{1}{y^t_{k'}} \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) ) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } p(l \mid x) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline
\end{split}
$$
最终,为了通过softmax层传播CTCLoss的梯度,需要计算目标函数与 logits $u^t_k$的偏微分,即Eq. 16:
$$
\begin{align*}
\hat{\alpha}_t(s) & \overset{def}{=} \frac{ \alpha_t(s) }{ C_t } ,\enspace C_t \overset{def}{=} \sum_s \alpha_t(s)
\newline
\hat{\beta}_t(s) & \overset{def}{=} \frac{ \beta_t(s) }{ D_t } ,\enspace D_t \overset{def}{=} \sum_s \beta_t(s)
\newline
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \tag{16}
\newline
\end{align*}
$$
### 2.1 总结
* 通过动态规划算法计算$\alpha_t(s)$ 和 $\beta_t(s)$
* 通过$\alpha_t(s)$ 计算 $p(l \mid x)=\alpha_T(\mid l' \mid) + \alpha_T(\mid l' \mid -1)$
* 通过$\alpha_t(s)$ 和 $\beta_t(s)$ 计算CTcLoss函数的导数:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s)
\newline
&= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s)
\newline
\end{split}
\tag{16}
$$
## Reference
[[1] A. Graves, S. Fernandez, F. Gomez, J. Schmidhuber. Connectionist Temporal lassification: Labeling Unsegmented Sequence Data with Recurrent Neural Networks. ICML 2006, Pittsburgh, USA, pp. 369-376.](http://www.cs.toronto.edu/~graves/icml_2006.pdf)
[[2] Sequence ModelingWith CTC](https://distill.pub/2017/ctc/)
[[3] NLP 之 CTC Loss 的工作原理](https://www.jianshu.com/p/e073c9d91b20)
[[4] The Softmax function and its derivative](https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/)
[[5] CTC Algorithm Explained Part 1:Training the Network(CTC算法详解之训练篇)](https://xiaodu.io/ctc-explained/)
### 2.3 CTC梯度推导
回顾下之前的公式,便于理解后续推导过程。
$$
p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \\
\begin{equation}
\alpha_t(s) \beta_t(s) = \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(l):} } y^t_{l'_s} \prod_{t=1}^T y^t_{\pi_t}
\end{equation}
$$
其中Eq. 15的计算过程如下:
$$
\begin{align*}
\frac{\part p(
l \mid x)}{\part y_k^t}
& = \sum_{s \in lab(z,k)} \frac{ \part \frac{ \alpha_t(s) \beta_t(s)}{y_{k}^t}}{\part y_k^t}
\newline
& = \sum_{s \in lab(z,k)} \frac{(\alpha_t(s)\beta_t(s))’y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{( \prod_{t'=1}^{t-1} y^{t'}_{\pi_{t'}} \cdot y_k^t \cdot y_k^t \cdot \prod_{t'=t+1}^{T} y^{t'}_{\pi_{t'}} )’ y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{2\alpha_t(s)\beta_t(s) - \alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \sum_{s \in lab(z,k)} \frac{\alpha_t(s)\beta_t(s)}{{y_k^t}^2}
\newline
&= \frac{1}{{y_k^t}^2} \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \tag{1} \newline
\end{align*}
$$
NLL的公式推导如下:
$$
\begin{split}
\frac{\part {ln(p(l \mid x))} }{ \part y^t_k }
&= \frac{1}{p(l \mid x)} \frac{ \part{p(l \mid x)} }{ \part y_k^t } \newline
&= \frac{1}{p(l \mid x) {y^t_k}^2 } \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s)
\end{split}
\tag{2}
$$
已经算出了CTCLoss对于 $y_k^t$ 的梯度,接下来我们需要计算 CTCLoss对于$u^t_k$(logits)的梯度。套用链式法则,并替换$y^t_k$ 为 $y^t_{k'}$,结果如下图。图中 $k'$ 表示vocab中的某一个token,$K$ 是vocab的大小。

图中公式4根据链式法则得到:
$$
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
= - \sum_{k'=1}^{K} \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'} }{ \part u^t_k } \tag{4}
$$
图中公式3是softmax的梯度,参考 [4],计算过程如下:
$$
softmax(j) = S_j = \frac{ e^{a_j} }{ \sum_{k=1}^K e^{a_k} }, \enspace \forall j \in 1 \dots K
$$
$$
\begin{split}
\frac{ \part S_i }{ \part a_j}
&= \frac{ \part (\frac{ e^{ a_i } }{ \sum_k e^{ a_k } }) } { \part a_j }
\newline
&=
\begin{cases}
\frac{ e^a_i \sum - e^a_j e^a_i }{ \sum^2 }
&= \frac{ e^a_i }{ \sum } \frac{ \sum - e^a_j }{ \sum } \newline
&= S_i(1-S_j) & \text{i = j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\newline
\frac{ 0 - e^a_j e^a_i }{ \sum^2 }
&= - \frac{ e^a_j }{ \sum } \frac{ e^a_i }{ \sum } \newline
&= -S_j S_i & \text{i $\neq$ j, $\sum$ stands for $\sum_{k=1}^K e^a_k$}
\end{cases}
\newline
&=
\begin{cases}
S_i(1 - S_j) & \text{$i = j$}
\newline
-S_j S_i = S_i (0 - S_j) & \text{$i \neq j$}
\end{cases}
\newline
&= S_i (\delta_{ij} - S_j )
\end{split}
\tag{3}
$$
$$
\delta_{ij} =
\begin{cases}
1 & \text{if i = j} \newline
0 & \text{otherwise}
\end{cases}
$$
下图中黄色框中的部分表示公式(1),即遍历所有的vocab中的token,其结果是$p(l \mid x)$。这是因为label $l$ 中的token一定在vocab中,且 $s \in lab(l, k')$ 可以是空集。当 $k'$ 在 l 中,s 则为label中token是$k'$的概率;当$k'$不在l中,s为空,概率为0。

公式(2),(3)带入(4),并结合公式(1)的结果如上图右边,即:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &=
- \sum_{k'=1}^K \frac{ \part ln(p(l \mid x)) }{ \part y^t_{k'} } \frac{ \part y^t_{k'}}{ \part u^t_k } \newline
&= - \sum_{k'=1}^K \frac{ y^t_{k'}( \delta_{kk'} - y^t_k ) }{ p(l \mid x) {y^t_{k'}}^2 } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= - \sum_{k'=1}^K \frac{ \delta_{kk'} - y^t_k }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t_k - \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \sum_{k'=1}^K \frac{ y^t }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } ( \sum_{k'=1}^K \frac{1}{y^t_{k'}} \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) ) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= \frac{ y^t_k }{ p(l \mid x) } p(l \mid x) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline
\end{split}
$$
最终,为了通过softmax层传播CTCLoss的梯度,需要计算目标函数与 logits $u^t_k$的偏微分,即Eq. 16:
$$
\begin{align*}
\hat{\alpha}_t(s) & \overset{def}{=} \frac{ \alpha_t(s) }{ C_t } ,\enspace C_t \overset{def}{=} \sum_s \alpha_t(s)
\newline
\hat{\beta}_t(s) & \overset{def}{=} \frac{ \beta_t(s) }{ D_t } ,\enspace D_t \overset{def}{=} \sum_s \beta_t(s)
\newline
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k } &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \tag{16}
\newline
\end{align*}
$$
### 2.1 总结
* 通过动态规划算法计算$\alpha_t(s)$ 和 $\beta_t(s)$
* 通过$\alpha_t(s)$ 计算 $p(l \mid x)=\alpha_T(\mid l' \mid) + \alpha_T(\mid l' \mid -1)$
* 通过$\alpha_t(s)$ 和 $\beta_t(s)$ 计算CTcLoss函数的导数:
$$
\begin{split}
- \frac{ \part ln(p(l \mid x)) }{ \part u^t_k }
&= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s)
\newline
&= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s)
\newline
\end{split}
\tag{16}
$$
## Reference
[[1] A. Graves, S. Fernandez, F. Gomez, J. Schmidhuber. Connectionist Temporal lassification: Labeling Unsegmented Sequence Data with Recurrent Neural Networks. ICML 2006, Pittsburgh, USA, pp. 369-376.](http://www.cs.toronto.edu/~graves/icml_2006.pdf)
[[2] Sequence ModelingWith CTC](https://distill.pub/2017/ctc/)
[[3] NLP 之 CTC Loss 的工作原理](https://www.jianshu.com/p/e073c9d91b20)
[[4] The Softmax function and its derivative](https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/)
[[5] CTC Algorithm Explained Part 1:Training the Network(CTC算法详解之训练篇)](https://xiaodu.io/ctc-explained/)