|
|
4 years ago | |
|---|---|---|
| .. | ||
| README.es.md | 4 years ago | |
| README.ko.md | 4 years ago | |
README.ko.md
K-Means clustering
🎥 영상을 보려면 이미지 클릭: Andrew Ng explains clustering
강의 전 퀴즈
이 강의에서, Scikit-learn과 함께 이전에 가져온 나이지리아 음악 데이터셋으로 클러스터 제작 방식을 배울 예정입니다. Clustering을 위한 K-Means 기초를 다루게 됩니다. 참고로, 이전 강의에서 배웠던대로, 클러스터로 작업하는 여러 방식이 있고 데이터를 기반한 방식도 있습니다. 가장 일반적 clustering 기술인 K-Means을 시도해보려고 합니다. 시작해봅니다!
다음 용어를 배우게 됩니다:
- Silhouette scoring
- Elbow method
- Inertia
- Variance
소개
K-Means Clustering은 신호 처리 도메인에서 파생된 방식입니다. observations 계열로서 데이터 그룹을 'k' 클러스터로 나누고 분할하며 사용했습니다. 각자 observation은 가까운 'mean', 또는 클러스터의 중심 포인트에 주어진 정밀한 데이터 포인트를 그룹으로 묶기 위해서 작동합니다.
클러스터는 포인트(또는 'seed')와 일치하는 영역을 포함한, Voronoi diagrams으로 시각화할 수 있습니다.
infographic by Jen Looper
K-Means clustering은 executes in a three-step process로 처리됩니다:
- 알고리즘은 데이터셋에서 샘플링한 중심 포인트의 k-number를 선택합니다. 반복합니다:
- 가장 가까운 무게 중심에 각자 샘플을 할당합니다.
- 이전의 무게 중심에서 할당된 모든 샘플의 평균 값을 가지면서 새로운 무게 중심을 만듭니다.
- 그러면, 새롭고 오래된 무게 중심 사이의 거리를 계산하고 무계 중심이 안정될 때까지 반복합니다.
K-Means을 사용한 한 가지 약점은 무게 중심의 숫자를, 'k'로 해야 된다는 사실입니다. 다행스럽게 'elbow method'는 'k' 값을 좋게 시작할 수 있게 추정하는 데 도움을 받을 수 있습니다. 몇 분동안 시도할 예정입니다.
전제 조건
마지막 강의에서 했던 데이터를 가져와서 미리 정리한 이 강의의 notebook.ipynb 파일로 작업할 예정입니다.
연습 - 준비하기
노래 데이터를 다시 보는 것부터 시작합니다.
-
각 열에
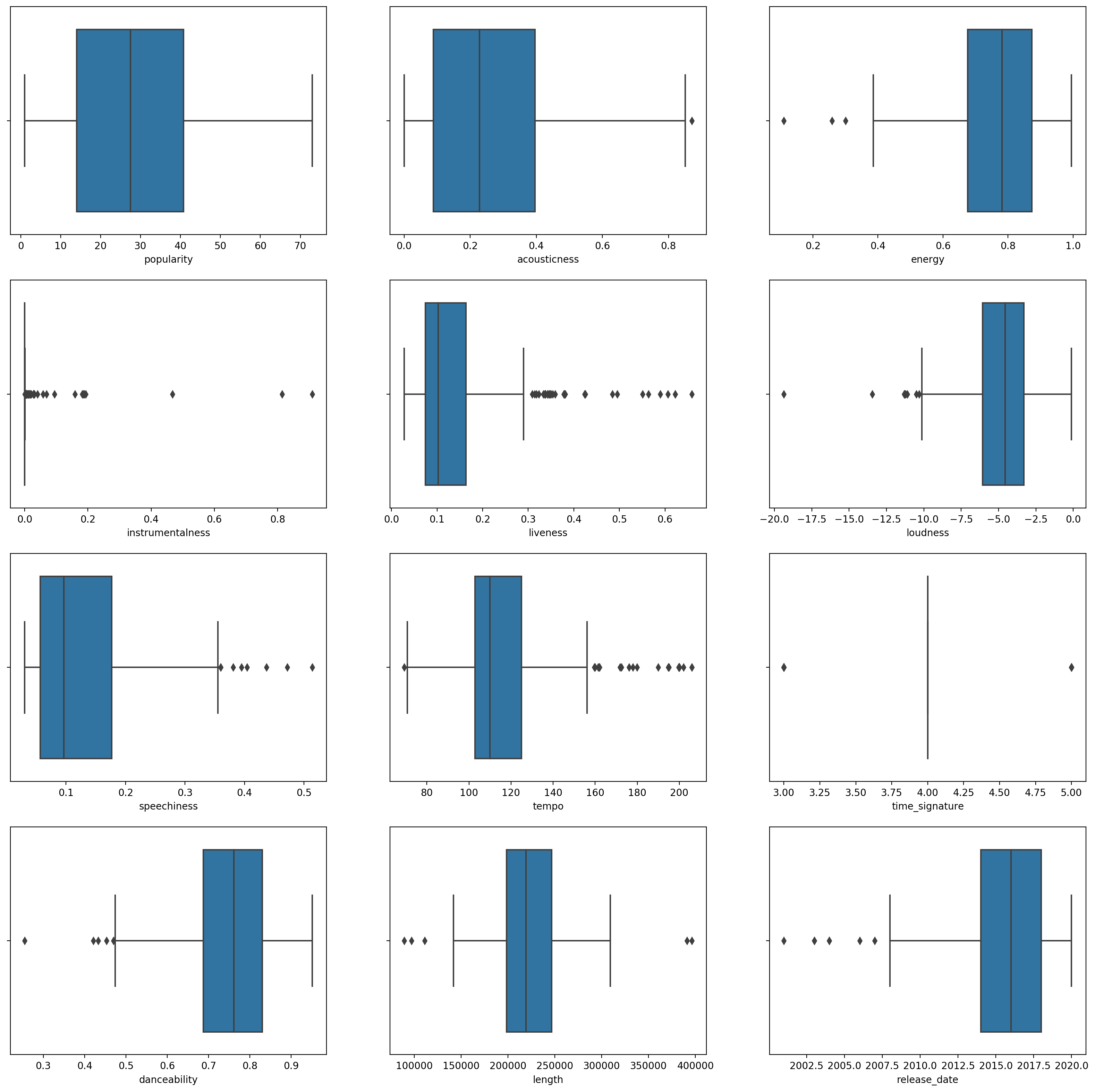
boxplot()을 불러서, boxplot을 만듭니다:plt.figure(figsize=(20,20), dpi=200) plt.subplot(4,3,1) sns.boxplot(x = 'popularity', data = df) plt.subplot(4,3,2) sns.boxplot(x = 'acousticness', data = df) plt.subplot(4,3,3) sns.boxplot(x = 'energy', data = df) plt.subplot(4,3,4) sns.boxplot(x = 'instrumentalness', data = df) plt.subplot(4,3,5) sns.boxplot(x = 'liveness', data = df) plt.subplot(4,3,6) sns.boxplot(x = 'loudness', data = df) plt.subplot(4,3,7) sns.boxplot(x = 'speechiness', data = df) plt.subplot(4,3,8) sns.boxplot(x = 'tempo', data = df) plt.subplot(4,3,9) sns.boxplot(x = 'time_signature', data = df) plt.subplot(4,3,10) sns.boxplot(x = 'danceability', data = df) plt.subplot(4,3,11) sns.boxplot(x = 'length', data = df) plt.subplot(4,3,12) sns.boxplot(x = 'release_date', data = df)이 데이터는 약간의 노이즈가 있습니다: 각 열을 boxplot으로 지켜보면 아웃라이어를 볼 수 있습니다.
데이터셋을 찾고 이 아웃라이어를 제거하는 대신에, 데이터는 꽤 작아지게 됩니다.
-
지금부터, clustering 연습에서 사용할 열을 선택합니다. 유사한 범위로 하나 선택하고
artist_top_genre열을 숫자 데이터로 인코딩합니다:from sklearn.preprocessing import LabelEncoder le = LabelEncoder() X = df.loc[:, ('artist_top_genre','popularity','danceability','acousticness','loudness','energy')] y = df['artist_top_genre'] X['artist_top_genre'] = le.fit_transform(X['artist_top_genre']) y = le.transform(y) -
이제 얼마나 많은 클러스터를 타겟으로 잡을지 선택해야 합니다. 데이터셋에서 조각낸 3개 장르가 있으므로, 3개를 시도합니다:
from sklearn.cluster import KMeans nclusters = 3 seed = 0 km = KMeans(n_clusters=nclusters, random_state=seed) km.fit(X) # Predict the cluster for each data point y_cluster_kmeans = km.predict(X) y_cluster_kmeans
데이터 프레임의 각 열에서 예측된 클러스터 (0, 1,또는 2)로 배열을 출력해서 볼 수 있습니다.
-
배열로 'silhouette score'를 계산합니다:
from sklearn import metrics score = metrics.silhouette_score(X, y_cluster_kmeans) score
Silhouette score
1에 근접한 silhouette score를 찾아봅니다. 이 점수는 -1에서 1까지 다양하며, 클러스터가 밀접하여 다른 것과 잘-분리됩니다. 0 근접 값은 주변 클러스터의 decision boundary에 매우 가까운 샘플과 함께 클러스터를 오버랩헤서 니타냅니다. source.
.53 점이므로, 중간에 위치합니다. 데이터가 이 clustering 타입에 특히 잘-맞지 않다는 점을 나타내고 있지만, 계속 진행합니다.
연습 - 모델 만들기
-
KMeans을 import 하고 clustering 처리를 시작합니다.from sklearn.cluster import KMeans wcss = [] for i in range(1, 11): kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42) kmeans.fit(X) wcss.append(kmeans.inertia_)여기 설명을 뒷받침할 몇 파트가 있습니다.
🎓 range: clustering 프로세스의 반복입니다
🎓 random_state: "Determines random number generation for centroid initialization."source
🎓 WCSS: "within-cluster sums of squares"은 클러스터 무게 중심으로 클러스터에서 모든 포인트의 squared average 거리를 측정합니다. source.
🎓 Inertia: K-Means 알고리즘은 'inertia'를 최소로 유지하기 위해서 무게 중심을 선택하려고 시도합니다, "a measure of how internally coherent clusters are."source. 값은 각 반복에서 wcss 변수로 추가됩니다.
🎓 k-means++: Scikit-learn에서 'k-means++' 최적화를 사용할 수 있고, 무게 중심을 (일반적인) 거리로 각자 떨어져서 초기화하면, 아마 랜덤 초기화보다 더 좋은 결과로 이어질 수 있습니다.
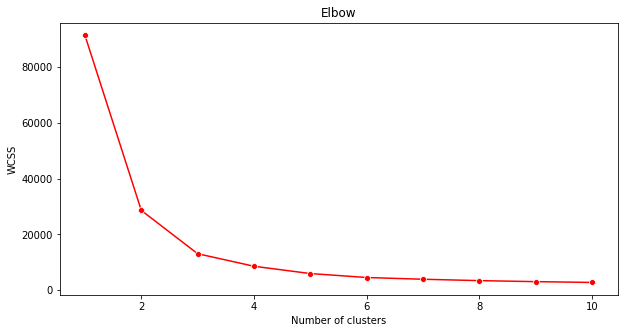
Elbow method
예전에 추측했던 것을 기반으로, 3개 노래 장르를 타겟팅 했으므로, 3게 클러스터를 선택해야 되었습니다. 그러나 그랬어야만 하나요?
-
'elbow method'을 사용해서 확인합니다.
plt.figure(figsize=(10,5)) sns.lineplot(range(1, 11), wcss,marker='o',color='red') plt.title('Elbow') plt.xlabel('Number of clusters') plt.ylabel('WCSS') plt.show()이전 단계에서 만들었던
wcss변수로, 최적 클러스터 수를 나타낼 elbow의 'bend'가 어디있는지 보여주는 차트를 만듭니다. 아마도 3 입니다!
연습 - 클러스터 보이기
-
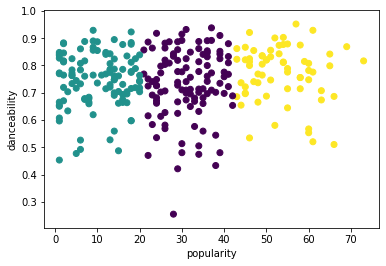
프로세스를 다시 시도하여, 이 시점에 3개 클러스터를 다시 설정하고, scatterplot으로 클러스터를 보여줍니다:
from sklearn.cluster import KMeans kmeans = KMeans(n_clusters = 3) kmeans.fit(X) labels = kmeans.predict(X) plt.scatter(df['popularity'],df['danceability'],c = labels) plt.xlabel('popularity') plt.ylabel('danceability') plt.show() -
모델 정확도를 확인합니다:
labels = kmeans.labels_ correct_labels = sum(y == labels) print("Result: %d out of %d samples were correctly labeled." % (correct_labels, y.size)) print('Accuracy score: {0:0.2f}'. format(correct_labels/float(y.size)))이 모델의 정확도는 매우 좋지 않으며, 클러스터의 형태가 왜 그랬는지 힌트를 줍니다.
이 데이터는 매우 불안정하며, 상관 관계가 낮고 열 값 사이에 편차가 커서 잘 클러스터될 수 없습니다. 사실, 만들어진 클러스터는 정의한 3개 장르 카테고리에 크게 영향받거나 뒤틀릴 수 있습니다. 학습 프로세스입니다!
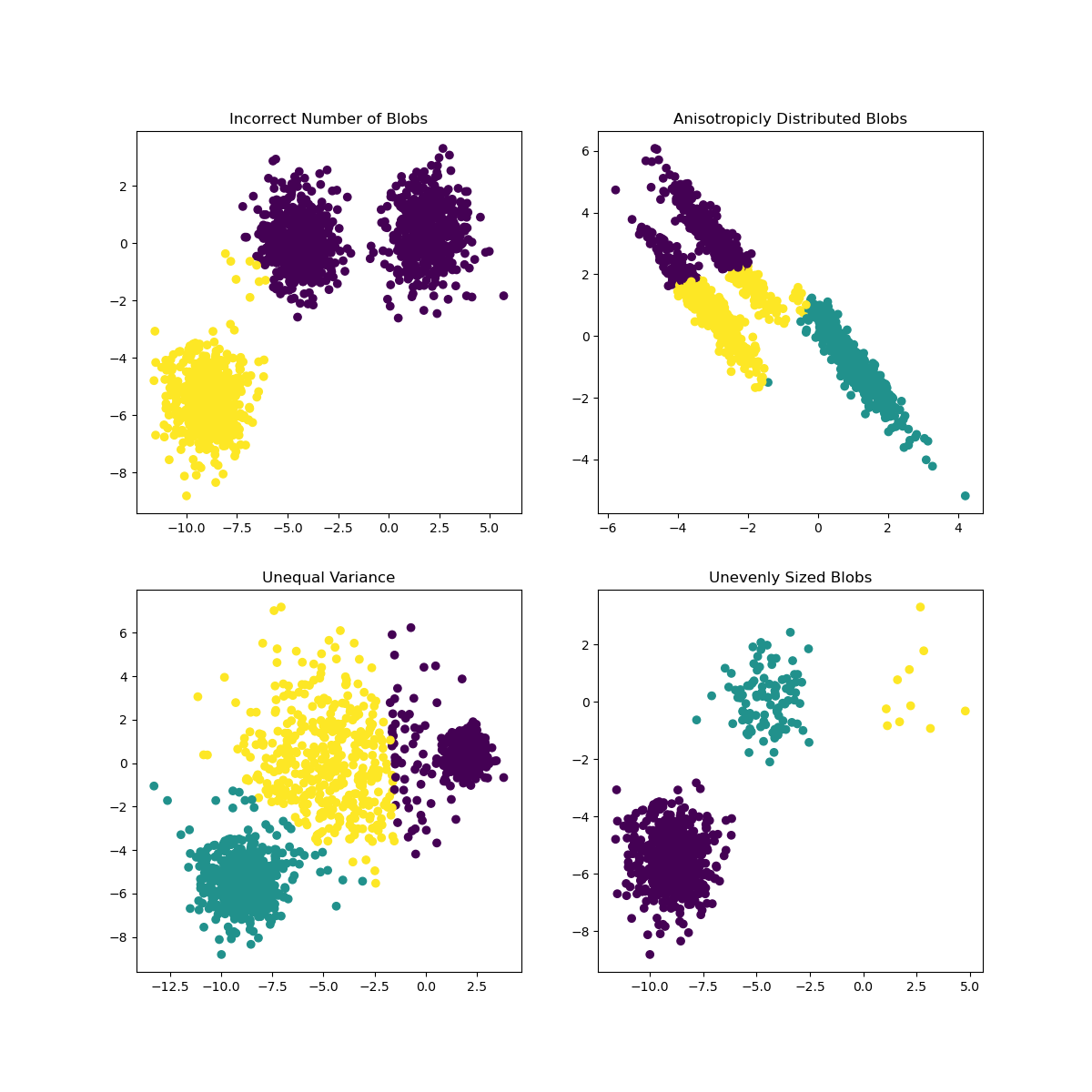
Scikit-learn 문서에, 클러스터가 매우 명확하지 않은 모델, 'variance' 문제가 있습니다:
Infographic from Scikit-learn
Variance
Variance는 "the average of the squared differences from the Mean."으로 정의되었습니다. source 이 clustering 문제의 컨텍스트에서, 데이터셋 숫자가 평균에서 너무 크게 이탈되어 데이터로 나타냅니다.
✅ 이 이슈를 해결할 모든 방식을 생각해보는 훌륭한 순간입니다. 데이터를 조금 트윅해볼까요? 다른 열을 사용해볼까요? 다른 알고리즘을 사용해볼까요? 힌트: scaling your data로 노멀라이즈하고 다른 컬럼을 테스트헤봅니다.
'variance calculator'로 좀 더 개념을 이해해봅니다.
🚀 도전
파라미터를 트윅하면서, 노트북으로 시간을 보냅니다. 데이터를 더 정리해서 (예시로, 아웃라이어 제거) 모델의 정확도를 개선할 수 있나요? 가중치로 주어진 데이터 샘플에서 더 가중치를 줄 수 있습니다. 괜찮은 클러스터를 만들기 위헤 어떤 다른 일을 할 수 있나요?
힌트: 데이터를 더 키워봅니다. 가까운 범위 조건에 비슷한 데이터 열을 만들고자 추가하는 표준 스케일링 코드를 노트북에 주석으로 남겼습니다. silhouette 점수가 낮아지는 동안, elbow 그래프의 'kink'가 주름 펴지는 것을 볼 수 있습니다. 데이터를 조정하지 않고 남기면 덜 분산된 데이터가 더 많은 가중치로 나를 수 있다는 이유입니다. here 이 문제를 조금 더 읽어봅니다.
강의 후 퀴즈
검토 & 자기주도 학습
Stanford의 K-Means 시뮬레이터를 찾아봅니다 here. 이 도구로 샘플 데이터 포인트를 시각화하고 무게 중심을 결정할 수 있습니다. 새로운 데이터로, 'update'를 클릭해서 수렴을 찾는데 얼마나 오래 걸리는지 봅니다. 데이터의 랜덤성, 클러스터 수와 무게 중심 수를 고칠 수 있습니다. 데이터를 그룹으로 묶기 위한 아이디어를 얻는 게 도움이 되나요?
또한, Stanford의 this handout on k-means을 찾아봅니다.