History

leestott c796f3dda8 🌐 Update translations via Co-op Translator		1 month ago
..
solution	🌐 Update translations via Co-op Translator	1 month ago
working	🌐 Update translations via Co-op Translator	1 month ago
README.md	🌐 Update translations via Co-op Translator	1 month ago
assignment.md	🌐 Update translations via Co-op Translator	1 month ago

README.md

Napovedovanje časovnih vrst z regresorjem podpornih vektorjev

V prejšnji lekciji ste se naučili uporabljati model ARIMA za napovedovanje časovnih vrst. Zdaj si bomo ogledali model Support Vector Regressor, ki je regresijski model za napovedovanje neprekinjenih podatkov.

Pre-lecture quiz

Uvod

V tej lekciji boste spoznali specifičen način gradnje modelov z SVM: Support Vector Machine za regresijo, ali SVR: Support Vector Regressor.

SVR v kontekstu časovnih vrst ¹

Preden razumemo pomen SVR pri napovedovanju časovnih vrst, je pomembno poznati naslednje koncepte:

Regresija: Tehnika nadzorovanega učenja za napovedovanje neprekinjenih vrednosti na podlagi danih vhodnih podatkov. Ideja je prilagoditi krivuljo (ali premico) v prostoru značilnosti, ki zajame največje število podatkovnih točk. Kliknite tukaj za več informacij.
Support Vector Machine (SVM): Vrsta modela nadzorovanega strojnega učenja, ki se uporablja za klasifikacijo, regresijo in zaznavanje odstopanj. Model je hiperploskev v prostoru značilnosti, ki v primeru klasifikacije deluje kot meja, v primeru regresije pa kot najboljša prilagoditvena premica. Pri SVM se pogosto uporablja funkcija jedra (Kernel function), ki transformira podatkovni niz v prostor z več dimenzijami, da postane lažje ločljiv. Kliknite tukaj za več informacij o SVM.
Support Vector Regressor (SVR): Vrsta SVM, ki najde najboljšo prilagoditveno premico (ki je v primeru SVM hiperploskev), ki zajame največje število podatkovnih točk.

Zakaj SVR? ¹

V prejšnji lekciji ste spoznali ARIMA, ki je zelo uspešna statistična linearna metoda za napovedovanje časovnih vrst. Vendar pa so podatki časovnih vrst pogosto nelinearni, kar linearni modeli ne morejo zajeti. V takih primerih sposobnost SVM, da upošteva nelinearnost podatkov pri regresijskih nalogah, naredi SVR uspešnega pri napovedovanju časovnih vrst.

Naloga - izdelava modela SVR

Prvi koraki za pripravo podatkov so enaki kot v prejšnji lekciji o ARIMA.

Odprite mapo /working v tej lekciji in poiščite datoteko notebook.ipynb. ²

Zaženite beležko in uvozite potrebne knjižnice: ²

import sys
sys.path.append('../../')

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from sklearn.svm import SVR
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape

Naložite podatke iz datoteke /data/energy.csv v Pandas dataframe in si jih oglejte: ²
```
energy = load_data('../../data')[['load']]
```

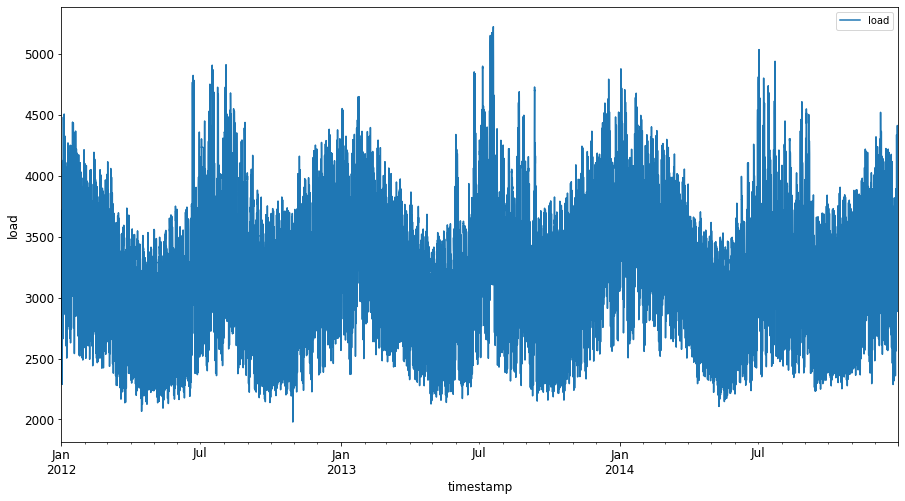
Prikažite vse razpoložljive podatke o energiji od januarja 2012 do decembra 2014: ²

energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

Zdaj pa izdelajmo naš model SVR.

Ustvarjanje učnih in testnih podatkovnih nizov

Ko so podatki naloženi, jih lahko ločite na učni in testni niz. Nato jih boste preoblikovali v podatkovni niz, ki temelji na časovnih korakih, kar bo potrebno za SVR. Model boste trenirali na učnem nizu. Ko bo model končal s treniranjem, boste ocenili njegovo natančnost na učnem nizu, testnem nizu in nato na celotnem podatkovnem nizu, da preverite splošno zmogljivost. Poskrbeti morate, da testni niz zajema poznejše obdobje v času od učnega niza, da zagotovite, da model ne pridobi informacij iz prihodnjih časovnih obdobij ² (situacija, znana kot Overfitting).

Dodelite dvomesečno obdobje od 1. septembra do 31. oktobra 2014 učnemu nizu. Testni niz bo vključeval dvomesečno obdobje od 1. novembra do 31. decembra 2014: ²
```
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
```

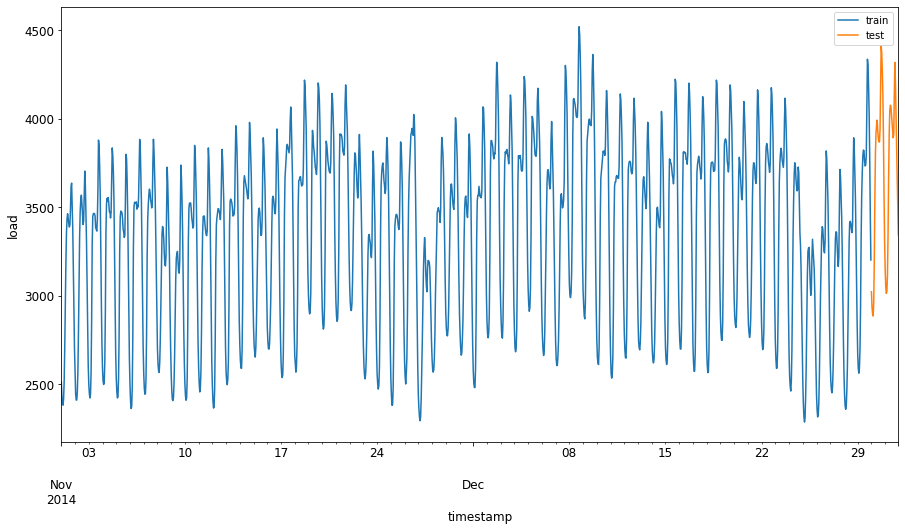
Vizualizirajte razlike: ²

energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

Priprava podatkov za treniranje

Zdaj morate pripraviti podatke za treniranje z izvajanjem filtriranja in skaliranja podatkov. Filtrirajte svoj podatkovni niz, da vključite samo potrebna časovna obdobja in stolpce, ter skalirajte podatke, da jih projicirate v interval 0,1.

Filtrirajte izvirni podatkovni niz, da vključite samo omenjena časovna obdobja na nizih in samo potrebni stolpec 'load' ter datum: ²

train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)

Training data shape:  (1416, 1)
Test data shape:  (48, 1)

Skalirajte učne podatke, da bodo v razponu (0, 1): ²

scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)

Zdaj skalirajte testne podatke: ²
```
test['load'] = scaler.transform(test)
```

Ustvarjanje podatkov s časovnimi koraki ¹

Za SVR preoblikujete vhodne podatke v obliko [batch, timesteps]. Tako obstoječe train_data in test_data preoblikujete tako, da dodate novo dimenzijo, ki se nanaša na časovne korake.

# Converting to numpy arrays
train_data = train.values
test_data = test.values

Za ta primer vzamemo timesteps = 5. Tako so vhodni podatki za model podatki za prve 4 časovne korake, izhod pa bodo podatki za 5. časovni korak.

timesteps=5

Pretvorba učnih podatkov v 2D tensor z uporabo ugnezdene listne komprehencije:

train_data_timesteps=np.array([[j for j in train_data[i:i+timesteps]] for i in range(0,len(train_data)-timesteps+1)])[:,:,0]
train_data_timesteps.shape

(1412, 5)

Pretvorba testnih podatkov v 2D tensor:

test_data_timesteps=np.array([[j for j in test_data[i:i+timesteps]] for i in range(0,len(test_data)-timesteps+1)])[:,:,0]
test_data_timesteps.shape

(44, 5)

Izbor vhodov in izhodov iz učnih in testnih podatkov:

x_train, y_train = train_data_timesteps[:,:timesteps-1],train_data_timesteps[:,[timesteps-1]]
x_test, y_test = test_data_timesteps[:,:timesteps-1],test_data_timesteps[:,[timesteps-1]]

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

(1412, 4) (1412, 1)
(44, 4) (44, 1)

Implementacija SVR ¹

Zdaj je čas za implementacijo SVR. Za več informacij o tej implementaciji si lahko ogledate to dokumentacijo. Za našo implementacijo sledimo tem korakom:

Definirajte model z uporabo SVR() in podajte hiperparametre modela: kernel, gamma, c in epsilon
Pripravite model za učne podatke z uporabo funkcije fit()
Izvedite napovedi z uporabo funkcije predict()

Zdaj ustvarimo model SVR. Tukaj uporabimo RBF kernel in nastavimo hiperparametre gamma, C in epsilon na 0.5, 10 in 0.05.

model = SVR(kernel='rbf',gamma=0.5, C=10, epsilon = 0.05)

Prilagoditev modela na učne podatke ¹

model.fit(x_train, y_train[:,0])

SVR(C=10, cache_size=200, coef0=0.0, degree=3, epsilon=0.05, gamma=0.5,
    kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

Izvedba napovedi modela ¹

y_train_pred = model.predict(x_train).reshape(-1,1)
y_test_pred = model.predict(x_test).reshape(-1,1)

print(y_train_pred.shape, y_test_pred.shape)

(1412, 1) (44, 1)

Izdelali ste svoj SVR! Zdaj ga moramo oceniti.

Ocenjevanje modela ¹

Za ocenjevanje najprej skaliramo podatke nazaj na našo izvirno lestvico. Nato za preverjanje zmogljivosti prikažemo izvirni in napovedani časovni niz ter natisnemo rezultat MAPE.

Skaliranje napovedanih in izvirnih izhodov:

# Scaling the predictions
y_train_pred = scaler.inverse_transform(y_train_pred)
y_test_pred = scaler.inverse_transform(y_test_pred)

print(len(y_train_pred), len(y_test_pred))

# Scaling the original values
y_train = scaler.inverse_transform(y_train)
y_test = scaler.inverse_transform(y_test)

print(len(y_train), len(y_test))

Preverjanje zmogljivosti modela na učnih in testnih podatkih ¹

Iz podatkovnega niza izvlečemo časovne oznake za prikaz na x-osi našega grafa. Upoštevajte, da uporabljamo prvih timesteps-1 vrednosti kot vhod za prvi izhod, zato se časovne oznake za izhod začnejo po tem.

train_timestamps = energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)].index[timesteps-1:]
test_timestamps = energy[test_start_dt:].index[timesteps-1:]

print(len(train_timestamps), len(test_timestamps))

1412 44

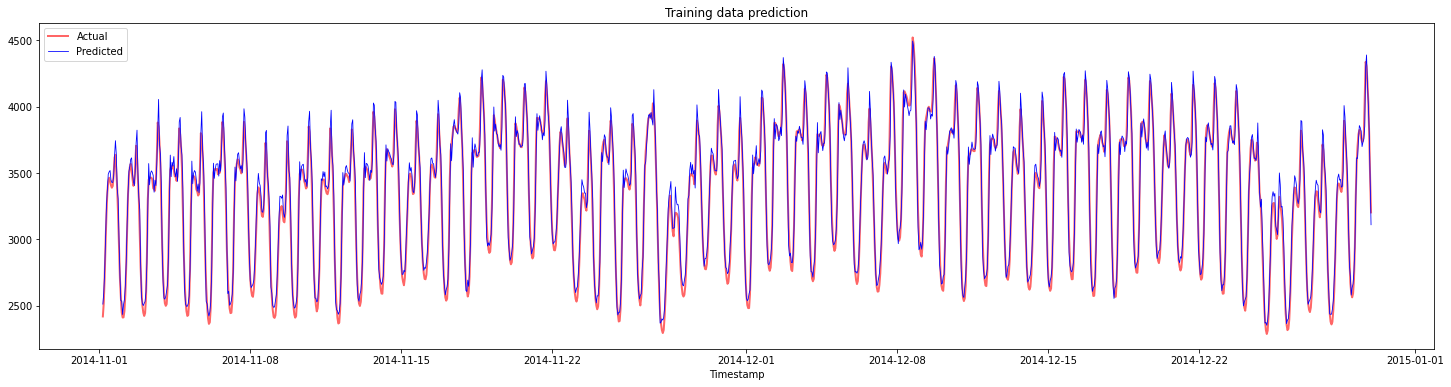
Prikaz napovedi za učne podatke:

plt.figure(figsize=(25,6))
plt.plot(train_timestamps, y_train, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(train_timestamps, y_train_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.title("Training data prediction")
plt.show()

Natisnite MAPE za učne podatke

print('MAPE for training data: ', mape(y_train_pred, y_train)*100, '%')

MAPE for training data: 1.7195710200875551 %

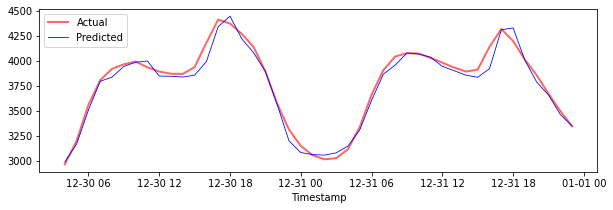
Prikaz napovedi za testne podatke

plt.figure(figsize=(10,3))
plt.plot(test_timestamps, y_test, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(test_timestamps, y_test_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

Natisnite MAPE za testne podatke

print('MAPE for testing data: ', mape(y_test_pred, y_test)*100, '%')

MAPE for testing data:  1.2623790187854018 %

🏆 Na testnem podatkovnem nizu imate zelo dober rezultat!

Preverjanje zmogljivosti modela na celotnem podatkovnem nizu ¹

# Extracting load values as numpy array
data = energy.copy().values

# Scaling
data = scaler.transform(data)

# Transforming to 2D tensor as per model input requirement
data_timesteps=np.array([[j for j in data[i:i+timesteps]] for i in range(0,len(data)-timesteps+1)])[:,:,0]
print("Tensor shape: ", data_timesteps.shape)

# Selecting inputs and outputs from data
X, Y = data_timesteps[:,:timesteps-1],data_timesteps[:,[timesteps-1]]
print("X shape: ", X.shape,"\nY shape: ", Y.shape)

Tensor shape:  (26300, 5)
X shape:  (26300, 4) 
Y shape:  (26300, 1)

# Make model predictions
Y_pred = model.predict(X).reshape(-1,1)

# Inverse scale and reshape
Y_pred = scaler.inverse_transform(Y_pred)
Y = scaler.inverse_transform(Y)

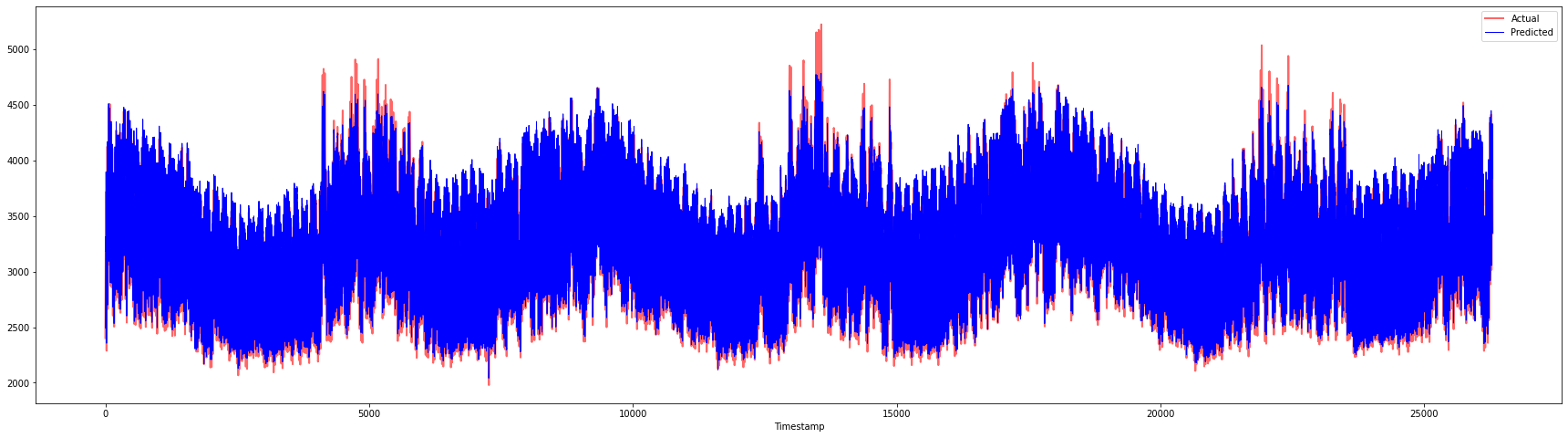
plt.figure(figsize=(30,8))
plt.plot(Y, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(Y_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

print('MAPE: ', mape(Y_pred, Y)*100, '%')

MAPE:  2.0572089029888656 %

🏆 Zelo lepi grafi, ki prikazujejo model z dobro natančnostjo. Odlično opravljeno!

🚀Izziv

Poskusite prilagoditi hiperparametre (gamma, C, epsilon) med ustvarjanjem modela in ocenite podatke, da vidite, kateri nabor hiperparametrov daje najboljše rezultate na testnih podatkih. Za več informacij o teh hiperparametrih si lahko ogledate dokument tukaj.
Poskusite uporabiti različne funkcije jedra za model in analizirajte njihovo zmogljivost na podatkovnem nizu. Koristen dokument najdete tukaj.
Poskusite uporabiti različne vrednosti za timesteps, da model pogleda nazaj za napovedovanje.

Post-lecture quiz

Pregled in samostojno učenje

Ta lekcija je bila namenjena predstavitvi uporabe SVR za napovedovanje časovnih vrst. Za več informacij o SVR si lahko ogledate ta blog. Ta dokumentacija o scikit-learn ponuja bolj celovito razlago o SVM na splošno, SVR in tudi druge podrobnosti implementacije, kot so različne funkcije jedra, ki jih je mogoče uporabiti, ter njihovi parametri.

Naloga

Novi model SVR

Zasluge

Omejitev odgovornosti:
Ta dokument je bil preveden z uporabo storitve za strojno prevajanje Co-op Translator. Čeprav si prizadevamo za natančnost, vas prosimo, da se zavedate, da lahko avtomatizirani prevodi vsebujejo napake ali netočnosti. Izvirni dokument v njegovem izvirnem jeziku je treba obravnavati kot avtoritativni vir. Za ključne informacije priporočamo strokovno človeško prevajanje. Ne prevzemamo odgovornosti za morebitna nesporazumevanja ali napačne razlage, ki izhajajo iz uporabe tega prevoda.

Besedilo, koda in izhod v tem razdelku je prispeval @AnirbanMukherjeeXD ↩︎
Besedilo, koda in izhod v tem razdelku je vzeto iz ARIMA ↩︎