|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 3 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.md | 3 weeks ago | |
| notebook.ipynb | 3 weeks ago | |
README.md
聚類簡介
聚類是一種無監督學習方法,假設數據集是未標籤的,或者其輸入未與預定義的輸出匹配。它使用各種算法來處理未標籤的數據,並根據數據中識別的模式進行分組。
🎥 點擊上方圖片觀看影片。在學習聚類機器學習的同時,欣賞一些尼日利亞舞廳音樂——這是 PSquare 在 2014 年推出的一首高評價歌曲。
課前測驗
簡介
聚類對於數據探索非常有用。讓我們看看它是否能幫助發現尼日利亞觀眾消費音樂方式的趨勢和模式。
✅ 花一分鐘思考聚類的用途。在現實生活中,聚類發生在你有一堆洗好的衣服需要分類到家人衣物的時候 🧦👕👖🩲。在數據科學中,聚類發生在試圖分析用戶偏好或確定任何未標籤數據集的特徵時。某種程度上,聚類幫助我們從混亂中找到秩序,就像整理襪子抽屜一樣。
🎥 點擊上方圖片觀看影片:麻省理工學院的 John Guttag 介紹聚類
在專業環境中,聚類可以用於確定市場細分,例如確定哪些年齡段購買哪些商品。另一個用途是異常檢測,比如從信用卡交易數據集中檢測欺詐行為。或者,你可以使用聚類來識別一批醫學掃描中的腫瘤。
✅ 花一分鐘思考你是否在銀行、電子商務或商業環境中遇到過聚類。
🎓 有趣的是,聚類分析起源於 1930 年代的人類學和心理學領域。你能想像它當時是如何被使用的嗎?
另外,你可以用它來分組搜索結果——例如按購物鏈接、圖片或評論分組。當你有一個大型數據集需要縮減並進行更細緻的分析時,聚類非常有用,因此這種技術可以在構建其他模型之前幫助了解數據。
✅ 一旦你的數據被組織成聚類,你可以為其分配一個聚類 ID。這種技術在保護數據集隱私時非常有用;你可以用聚類 ID 來引用數據點,而不是使用更具識別性的數據。你能想到其他使用聚類 ID 而不是聚類中其他元素來識別它的原因嗎?
在這個學習模組中深入了解聚類技術。
開始使用聚類
Scikit-learn 提供了多種方法來執行聚類。你選擇的方法將取決於你的使用案例。根據文檔,每種方法都有其各自的優勢。以下是 Scikit-learn 支持的方法及其適用場景的簡化表格:
| 方法名稱 | 使用場景 |
|---|---|
| K-Means | 通用,歸納式 |
| Affinity propagation | 多個、不均勻的聚類,歸納式 |
| Mean-shift | 多個、不均勻的聚類,歸納式 |
| Spectral clustering | 少量、均勻的聚類,轉導式 |
| Ward hierarchical clustering | 多個、受限的聚類,轉導式 |
| Agglomerative clustering | 多個、受限的、非歐幾里得距離的聚類,轉導式 |
| DBSCAN | 非平面幾何、不均勻的聚類,轉導式 |
| OPTICS | 非平面幾何、不均勻且密度可變的聚類,轉導式 |
| Gaussian mixtures | 平面幾何,歸納式 |
| BIRCH | 含有異常值的大型數據集,歸納式 |
🎓 我們如何創建聚類與我們如何將數據點分組密切相關。讓我們來解釋一些術語:
轉導式推理來自觀察到的訓練案例,這些案例映射到特定的測試案例。歸納式推理來自訓練案例,這些案例映射到通用規則,然後才應用於測試案例。
一個例子:假設你有一個部分標籤的數據集。一些項目是“唱片”,一些是“CD”,一些是空白的。你的任務是為空白項目提供標籤。如果你選擇歸納式方法,你會訓練一個模型來尋找“唱片”和“CD”,並將這些標籤應用於未標籤數據。這種方法可能無法很好地分類實際上是“磁帶”的項目。而轉導式方法則更有效地處理這些未知數據,因為它努力將相似的項目分組,然後為整個組分配一個標籤。在這種情況下,聚類可能反映“圓形音樂物品”和“方形音樂物品”。
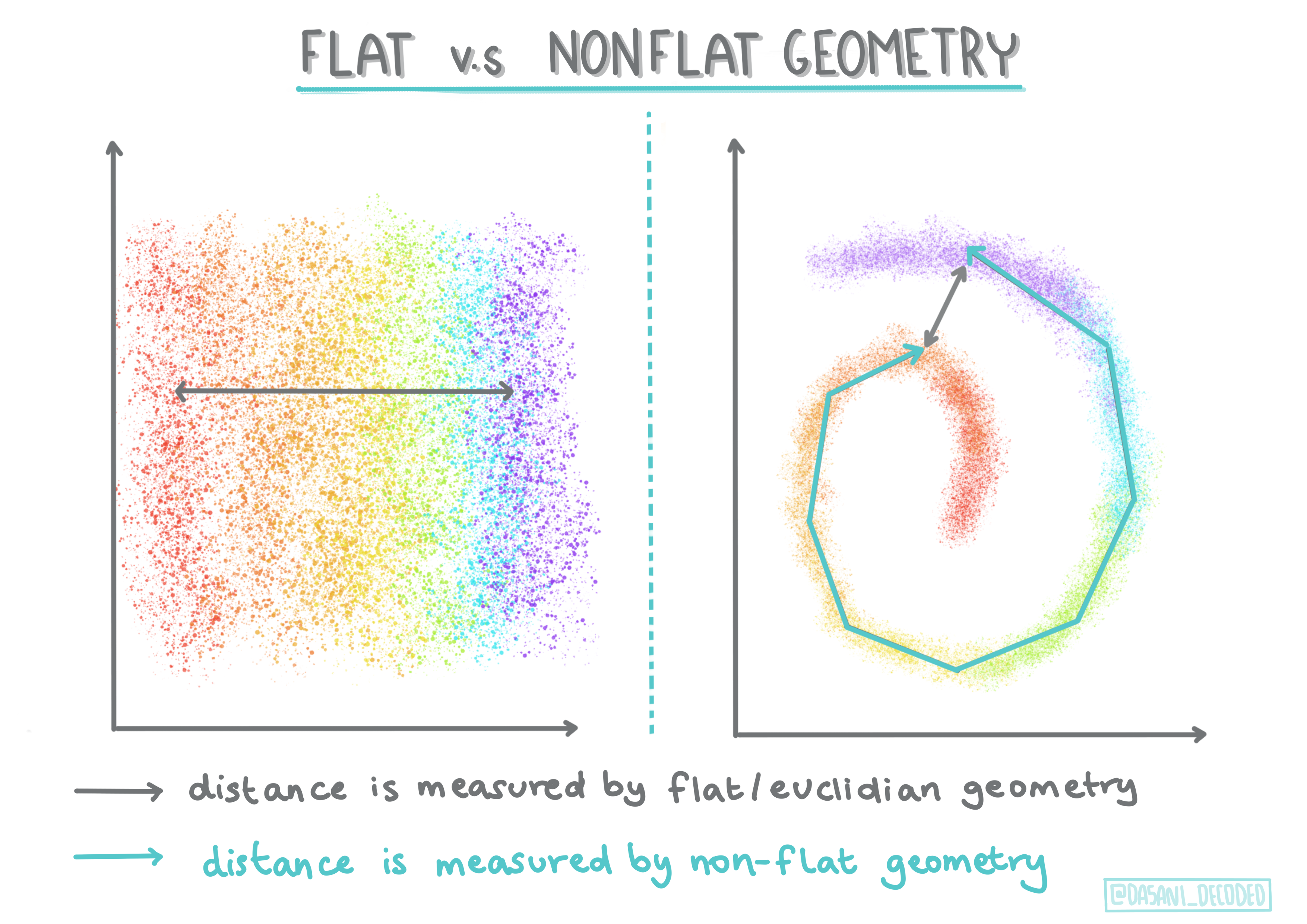
來自數學術語,非平面與平面幾何指的是通過“平面”(歐幾里得)或“非平面”(非歐幾里得)幾何方法測量點之間的距離。
'平面'在此上下文中指的是歐幾里得幾何(部分內容在學校被教為“平面幾何”),而非平面指的是非歐幾里得幾何。幾何與機器學習有什麼關係?作為兩個都根植於數學的領域,必須有一種通用的方法來測量聚類中點之間的距離,這可以根據數據的性質以“平面”或“非平面”的方式完成。歐幾里得距離是通過兩點之間的線段長度來測量的。非歐幾里得距離則沿曲線測量。如果你的數據在可視化時似乎不在一個平面上,你可能需要使用專門的算法來處理它。
資訊圖表由 Dasani Madipalli 提供
🎓 '距離'
聚類由其距離矩陣定義,例如點之間的距離。這種距離可以通過幾種方式測量。歐幾里得聚類由點值的平均值定義,並包含一個“中心點”或中心點。因此,距離是通過到該中心點的距離來測量的。非歐幾里得距離則指“聚心點”,即最接近其他點的點。聚心點可以通過多種方式定義。
🎓 '受限'
受限聚類 在這種無監督方法中引入了“半監督”學習。點之間的關係被標記為“不能鏈接”或“必須鏈接”,因此對數據集施加了一些規則。
一個例子:如果一個算法在一批未標籤或半標籤數據上自由運行,它生成的聚類可能質量較差。在上述例子中,聚類可能會將“圓形音樂物品”、“方形音樂物品”、“三角形物品”和“餅乾”分組。如果給定一些約束或規則(“物品必須由塑料製成”,“物品需要能夠產生音樂”),這可以幫助“限制”算法做出更好的選擇。
🎓 '密度'
被認為“嘈雜”的數據被認為是“密集的”。檢查時,其每個聚類中點之間的距離可能被證明是更密集或更稀疏的,因此需要使用適當的聚類方法來分析這些數據。這篇文章展示了使用 K-Means 聚類與 HDBSCAN 算法探索具有不均勻聚類密度的嘈雜數據集的區別。
聚類算法
有超過 100 種聚類算法,其使用取決於手頭數據的性質。讓我們討論一些主要的算法:
-
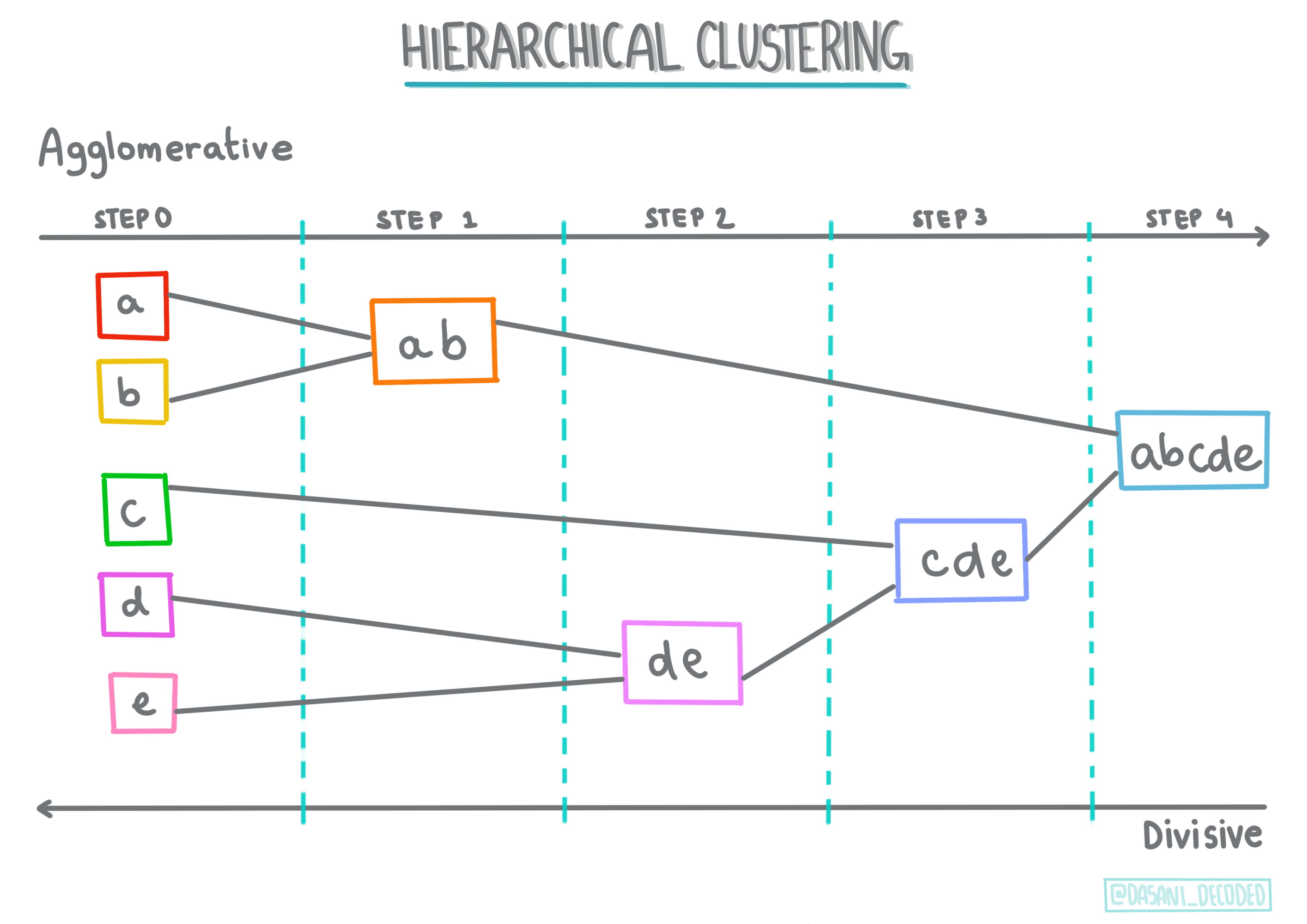
層次聚類。如果一個物體是通過其與附近物體的接近程度而分類的,而不是與更遠的物體分類,則聚類是基於其成員與其他物體的距離形成的。Scikit-learn 的凝聚聚類是層次聚類的一種。
資訊圖表由 Dasani Madipalli 提供
-
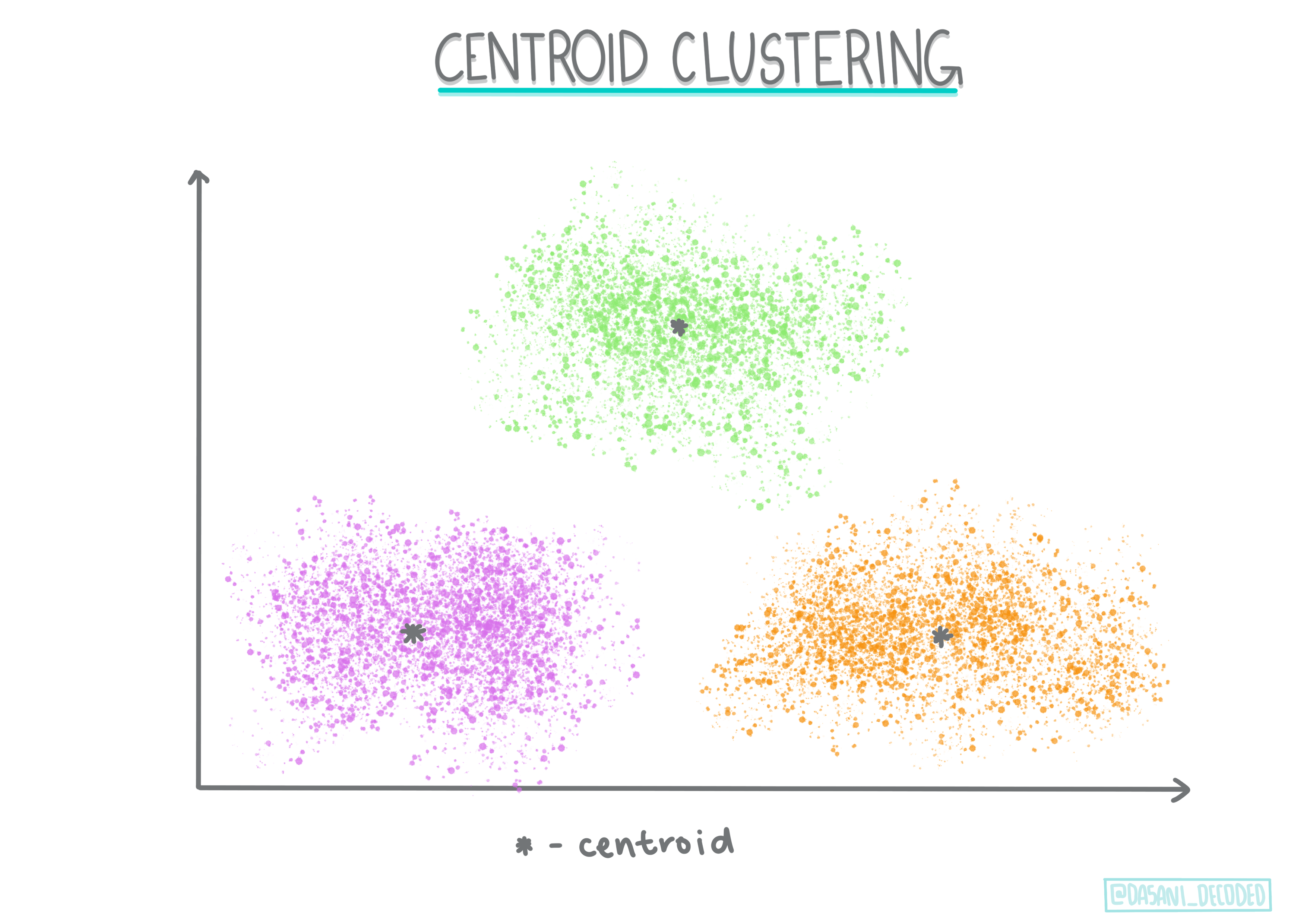
中心點聚類。這種流行的算法需要選擇“k”,即要形成的聚類數量,然後算法確定聚類的中心點並圍繞該點收集數據。K-means 聚類 是一種流行的中心點聚類方法。中心點由最近的平均值確定,因此得名。從聚類的平方距離被最小化。
資訊圖表由 Dasani Madipalli 提供
-
基於分佈的聚類。基於統計建模,基於分佈的聚類集中於確定數據點屬於某個聚類的概率,並據此分配。高斯混合方法屬於這種類型。
-
基於密度的聚類。數據點根據其密度或它們彼此之間的分組被分配到聚類中。遠離群體的數據點被認為是異常值或噪聲。DBSCAN、Mean-shift 和 OPTICS 屬於這種類型的聚類。
-
基於網格的聚類。對於多維數據集,創建一個網格,並將數據分配到網格的單元中,從而創建聚類。
練習 - 聚類你的數據
聚類作為一種技術在適當的可視化幫助下效果更佳,因此讓我們從可視化我們的音樂數據開始。這個練習將幫助我們決定針對這些數據的性質最有效使用哪種聚類方法。
-
打開此文件夾中的 notebook.ipynb。
-
導入
Seaborn套件以進行良好的數據可視化。!pip install seaborn -
從 nigerian-songs.csv 附加歌曲數據。加載一個包含歌曲數據的數據框。通過導入庫並輸出數據來準備探索這些數據:
import matplotlib.pyplot as plt import pandas as pd df = pd.read_csv("../data/nigerian-songs.csv") df.head()檢查數據的前幾行:
name album artist artist_top_genre release_date length popularity danceability acousticness energy instrumentalness liveness loudness speechiness tempo time_signature 0 Sparky Mandy & The Jungle Cruel Santino alternative r&b 2019 144000 48 0.666 0.851 0.42 0.534 0.11 -6.699 0.0829 133.015 5 1 shuga rush EVERYTHING YOU HEARD IS TRUE Odunsi (The Engine) afropop 2020 89488 30 0.71 0.0822 0.683 0.000169 0.101 -5.64 0.36 129.993 3 2 LITT! LITT! AYLØ 獨立R&B 2018 207758 40 0.836 0.272 0.564 0.000537 0.11 -7.127 0.0424 130.005 4 3 Confident / Feeling Cool Enjoy Your Life Lady Donli 奈及利亞流行音樂 2019 175135 14 0.894 0.798 0.611 0.000187 0.0964 -4.961 0.113 111.087 4 4 wanted you rare. Odunsi (The Engine) 非洲流行音樂 2018 152049 25 0.702 0.116 0.833 0.91 0.348 -6.044 0.0447 105.115 4 -
獲取數據框的基本資訊,呼叫
info():df.info()輸出如下所示:
<class 'pandas.core.frame.DataFrame'> RangeIndex: 530 entries, 0 to 529 Data columns (total 16 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 name 530 non-null object 1 album 530 non-null object 2 artist 530 non-null object 3 artist_top_genre 530 non-null object 4 release_date 530 non-null int64 5 length 530 non-null int64 6 popularity 530 non-null int64 7 danceability 530 non-null float64 8 acousticness 530 non-null float64 9 energy 530 non-null float64 10 instrumentalness 530 non-null float64 11 liveness 530 non-null float64 12 loudness 530 non-null float64 13 speechiness 530 non-null float64 14 tempo 530 non-null float64 15 time_signature 530 non-null int64 dtypes: float64(8), int64(4), object(4) memory usage: 66.4+ KB -
通過呼叫
isnull()並驗證總和是否為 0,仔細檢查是否有空值:df.isnull().sum()看起來不錯:
name 0 album 0 artist 0 artist_top_genre 0 release_date 0 length 0 popularity 0 danceability 0 acousticness 0 energy 0 instrumentalness 0 liveness 0 loudness 0 speechiness 0 tempo 0 time_signature 0 dtype: int64 -
描述數據:
df.describe()release_date length popularity danceability acousticness energy instrumentalness liveness loudness speechiness tempo time_signature count 530 530 530 530 530 530 530 530 530 530 530 530 mean 2015.390566 222298.1698 17.507547 0.741619 0.265412 0.760623 0.016305 0.147308 -4.953011 0.130748 116.487864 3.986792 std 3.131688 39696.82226 18.992212 0.117522 0.208342 0.148533 0.090321 0.123588 2.464186 0.092939 23.518601 0.333701 min 1998 89488 0 0.255 0.000665 0.111 0 0.0283 -19.362 0.0278 61.695 3 25% 2014 199305 0 0.681 0.089525 0.669 0 0.07565 -6.29875 0.0591 102.96125 4 50% 2016 218509 13 0.761 0.2205 0.7845 0.000004 0.1035 -4.5585 0.09795 112.7145 4 75% 2017 242098.5 31 0.8295 0.403 0.87575 0.000234 0.164 -3.331 0.177 125.03925 4 max 2020 511738 73 0.966 0.954 0.995 0.91 0.811 0.582 0.514 206.007 5
🤔 如果我們使用的是無需標籤數據的無監督方法(如聚類),為什麼還要顯示帶有標籤的數據?在數據探索階段,這些標籤很有用,但對於聚類算法來說並非必要。你完全可以移除列標題,直接用列號來引用數據。
看看數據的一般值。注意,受歡迎度可以為 "0",這表示歌曲沒有排名。我們稍後會移除這些數據。
-
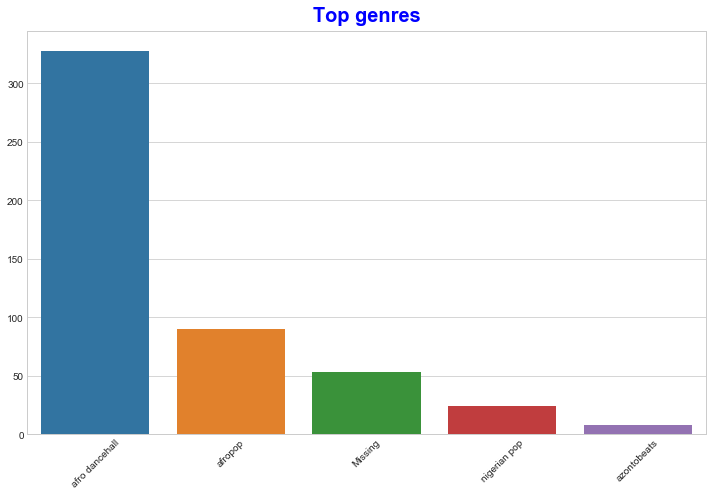
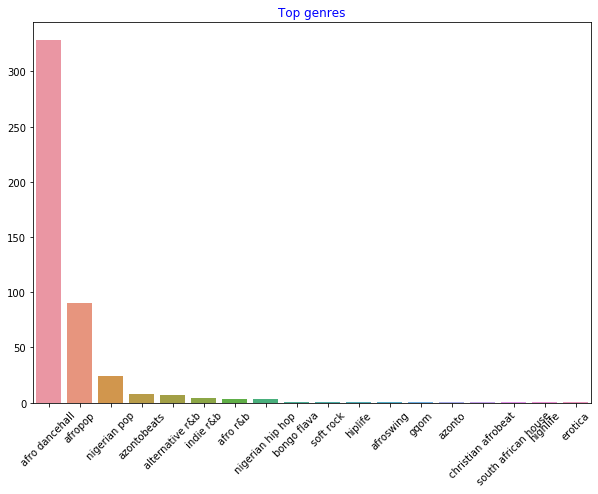
使用條形圖找出最受歡迎的音樂類型:
import seaborn as sns top = df['artist_top_genre'].value_counts() plt.figure(figsize=(10,7)) sns.barplot(x=top[:5].index,y=top[:5].values) plt.xticks(rotation=45) plt.title('Top genres',color = 'blue')
✅ 如果你想查看更多的前幾名數據,可以將 [:5] 改為更大的值,或者移除它以查看全部。
注意,當最受歡迎的類型被描述為 "Missing" 時,這表示 Spotify 沒有對其進行分類,因此我們需要將其移除。
-
通過篩選移除缺失數據:
df = df[df['artist_top_genre'] != 'Missing'] top = df['artist_top_genre'].value_counts() plt.figure(figsize=(10,7)) sns.barplot(x=top.index,y=top.values) plt.xticks(rotation=45) plt.title('Top genres',color = 'blue')現在重新檢查音樂類型:
-
顯然,前三大音樂類型在這個數據集中占據主導地位。我們專注於
afro dancehall、afropop和nigerian pop,並進一步篩選數據,移除任何受歡迎度為 0 的數據(這表示數據集中未被分類為受歡迎的歌曲,對我們的目的來說可以視為噪聲):df = df[(df['artist_top_genre'] == 'afro dancehall') | (df['artist_top_genre'] == 'afropop') | (df['artist_top_genre'] == 'nigerian pop')] df = df[(df['popularity'] > 0)] top = df['artist_top_genre'].value_counts() plt.figure(figsize=(10,7)) sns.barplot(x=top.index,y=top.values) plt.xticks(rotation=45) plt.title('Top genres',color = 'blue') -
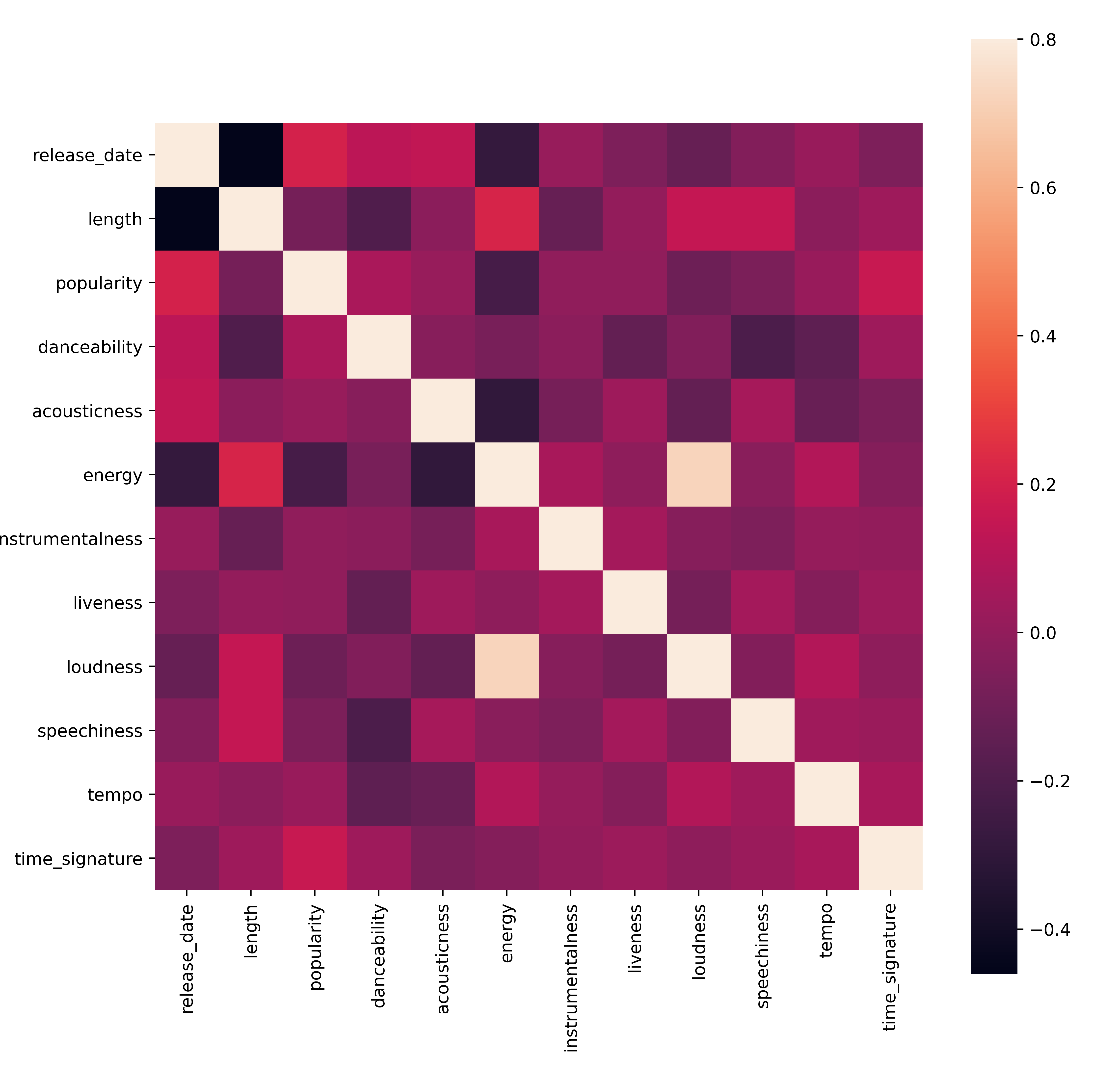
快速測試數據是否有特別強的相關性:
corrmat = df.corr(numeric_only=True) f, ax = plt.subplots(figsize=(12, 9)) sns.heatmap(corrmat, vmax=.8, square=True)唯一的強相關性是
energy和loudness之間,這並不令人驚訝,因為響亮的音樂通常充滿活力。除此之外,相關性相對較弱。看看聚類算法如何處理這些數據會很有趣。🎓 請注意,相關性並不意味著因果關係!我們有相關性的證據,但沒有因果關係的證據。一個有趣的網站 提供了一些強調這一點的視覺化內容。
在這個數據集中,歌曲的受歡迎度和舞蹈性是否存在某種趨同?使用 FacetGrid 可以看到無論音樂類型如何,都有一些同心圓的分佈。是否可能奈及利亞的品味在這些類型的舞蹈性上達到了一定的趨同水平?
✅ 嘗試不同的數據點(如 energy、loudness、speechiness)以及更多或不同的音樂類型。你能發現什麼?查看 df.describe() 表格,了解數據點的一般分佈。
練習 - 數據分佈
這三種音樂類型在受歡迎度和舞蹈性上的感知是否有顯著差異?
-
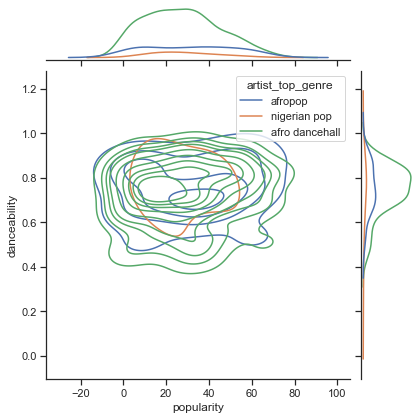
檢查我們的前三大音樂類型在受歡迎度和舞蹈性上的數據分佈,沿著給定的 x 和 y 軸。
sns.set_theme(style="ticks") g = sns.jointplot( data=df, x="popularity", y="danceability", hue="artist_top_genre", kind="kde", )你可以發現圍繞一個一般趨同點的同心圓,顯示數據點的分佈。
🎓 請注意,此示例使用的是 KDE(核密度估計)圖,該圖使用連續的概率密度曲線來表示數據。這在處理多個分佈時非常有用。
總的來說,這三種音樂類型在受歡迎度和舞蹈性上大致對齊。在這些大致對齊的數據中確定聚類將是一個挑戰:
-
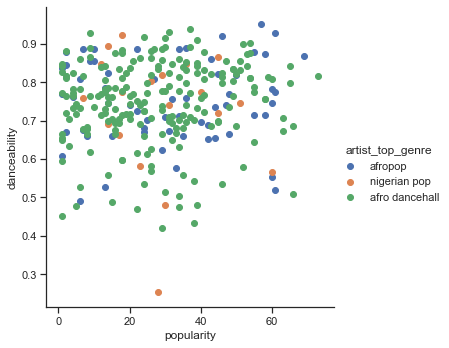
創建一個散點圖:
sns.FacetGrid(df, hue="artist_top_genre", height=5) \ .map(plt.scatter, "popularity", "danceability") \ .add_legend()同一軸上的散點圖顯示了類似的趨同模式
總的來說,對於聚類,你可以使用散點圖來顯示數據的聚類,因此掌握這種類型的可視化非常有用。在下一課中,我們將使用 k-means 聚類來探索這些數據中有趣的重疊群組。
🚀挑戰
為下一課做準備,製作一個關於你可能在生產環境中發現和使用的各種聚類算法的圖表。聚類試圖解決哪些問題?
課後測驗
回顧與自學
在應用聚類算法之前,正如我們所學,了解數據集的性質是個好主意。閱讀更多相關內容這裡
這篇有幫助的文章 介紹了不同聚類算法在不同數據形狀下的行為。
作業
免責聲明:
本文件使用 AI 翻譯服務 Co-op Translator 進行翻譯。儘管我們努力確保翻譯的準確性,但請注意,自動翻譯可能包含錯誤或不準確之處。原始語言的文件應被視為權威來源。對於關鍵資訊,建議使用專業人工翻譯。我們對因使用此翻譯而引起的任何誤解或錯誤解釋不承擔責任。