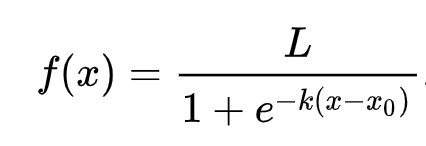History

leestott 1f5af4814d 🌐 Update translations via Co-op Translator		2 weeks ago
..
solution	🌐 Update translations via Co-op Translator	2 weeks ago
README.md	🌐 Update translations via Co-op Translator	2 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	2 weeks ago
notebook.ipynb	🌐 Update translations via Co-op Translator	3 weeks ago

README.md

Logisztikus regresszió kategóriák előrejelzésére

Előadás előtti kvíz

Ez a lecke elérhető R-ben is!

Bevezetés

Ebben az utolsó leckében a regresszióról, amely az egyik alapvető klasszikus gépi tanulási technika, megvizsgáljuk a logisztikus regressziót. Ezt a technikát arra használhatjuk, hogy mintázatokat fedezzünk fel bináris kategóriák előrejelzésére. Ez a cukorka csokoládé vagy sem? Ez a betegség fertőző vagy sem? Ez az ügyfél választja-e ezt a terméket vagy sem?

Ebben a leckében megtanulod:

Egy új könyvtár használatát az adatok vizualizálásához
Logisztikus regresszió technikáit

✅ Mélyítsd el a logisztikus regresszióval kapcsolatos tudásodat ebben a Learn modulban

Előfeltétel

A tökadatokkal való munka során már elég jól megismerkedtünk ahhoz, hogy felismerjük, van egy bináris kategória, amellyel dolgozhatunk: Color.

Építsünk egy logisztikus regressziós modellt, hogy előre jelezzük, adott változók alapján milyen színű lesz egy adott tök (narancs 🎃 vagy fehér 👻).

Miért beszélünk bináris osztályozásról egy regresszióval kapcsolatos leckében? Csak nyelvi kényelmi okokból, mivel a logisztikus regresszió valójában egy osztályozási módszer, bár lineáris alapú. Az adatok osztályozásának más módjairól a következő leckecsoportban tanulhatsz.

Fogalmazzuk meg a kérdést

A mi céljaink érdekében ezt binárisként fogalmazzuk meg: 'Fehér' vagy 'Nem fehér'. Az adatainkban van egy 'csíkos' kategória is, de kevés előfordulása van, így nem fogjuk használni. Ez amúgy is eltűnik, amikor eltávolítjuk az adatállományból a null értékeket.

🎃 Érdekesség: néha a fehér tököket 'szellem' tököknek hívjuk. Nem túl könnyű őket faragni, ezért nem olyan népszerűek, mint a narancssárgák, de nagyon jól néznek ki! Így a kérdésünket úgy is megfogalmazhatnánk: 'Szellem' vagy 'Nem szellem'. 👻

A logisztikus regresszióról

A logisztikus regresszió néhány fontos szempontból különbözik a korábban tanult lineáris regressziótól.

🎥 Kattints a fenti képre egy rövid videós áttekintésért a logisztikus regresszióról.

Bináris osztályozás

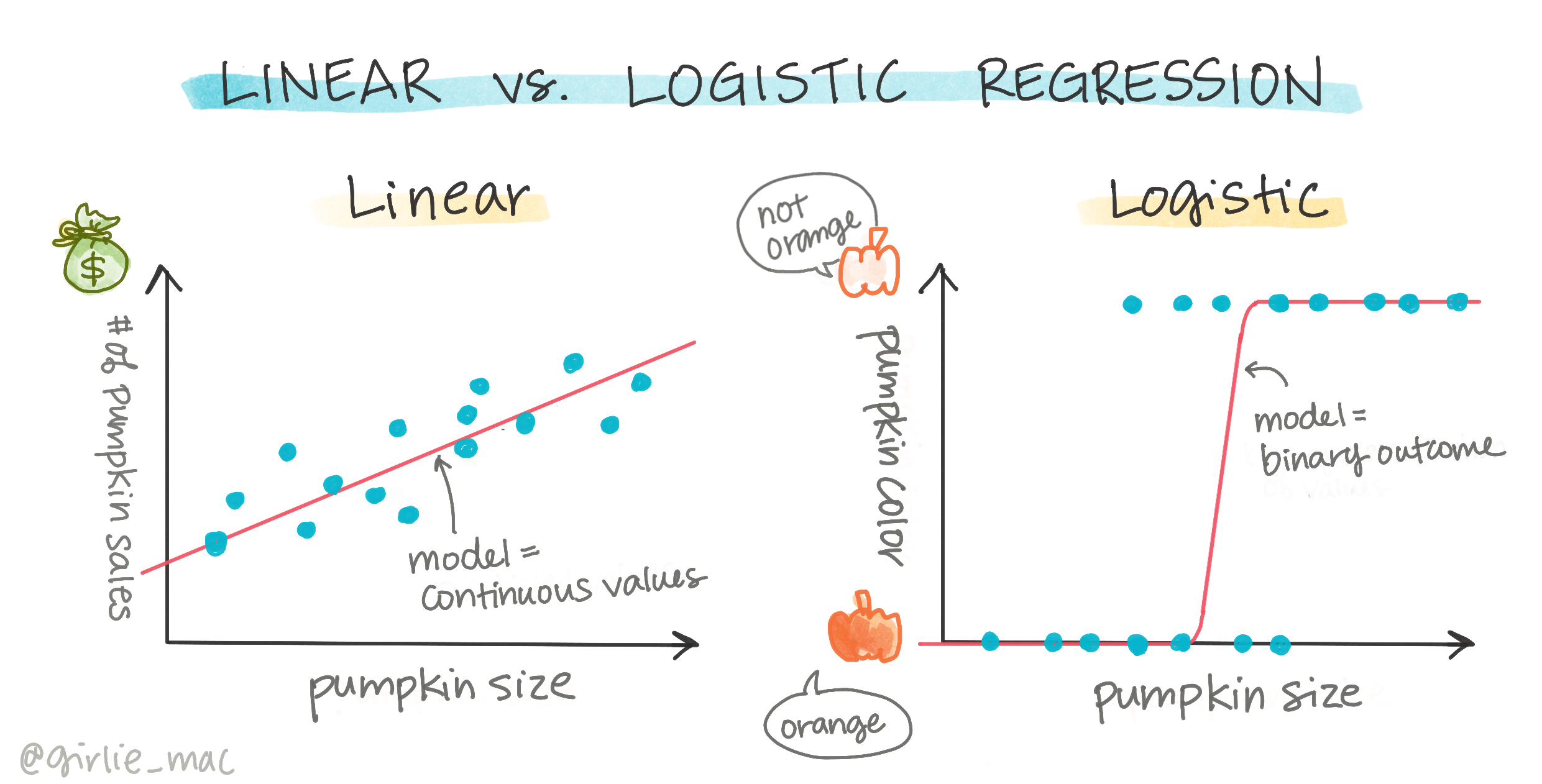
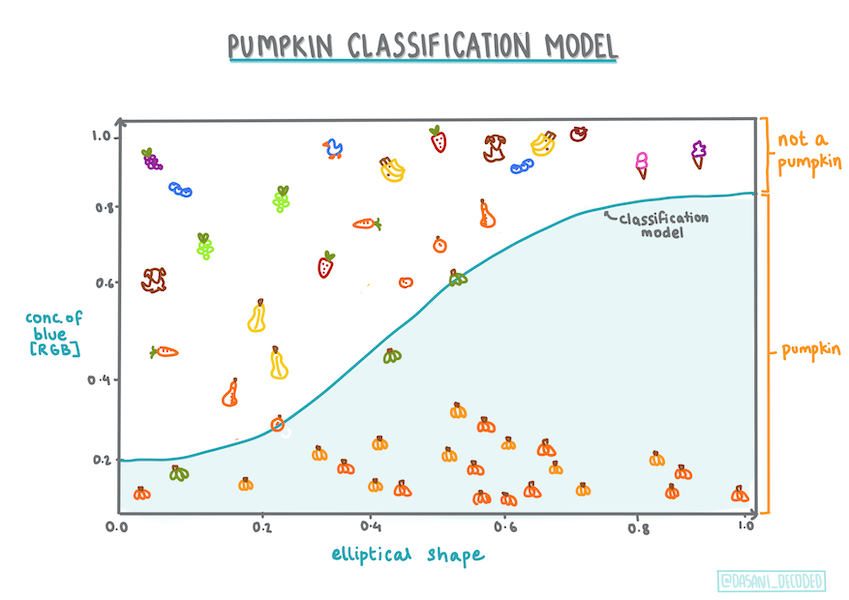
A logisztikus regresszió nem kínálja ugyanazokat a funkciókat, mint a lineáris regresszió. Az előbbi bináris kategóriáról ("fehér vagy nem fehér") ad előrejelzést, míg az utóbbi folyamatos értékeket képes előre jelezni, például a tök származási helye és betakarítási ideje alapján, mennyivel fog emelkedni az ára.

Infografika: Dasani Madipalli

Egyéb osztályozások

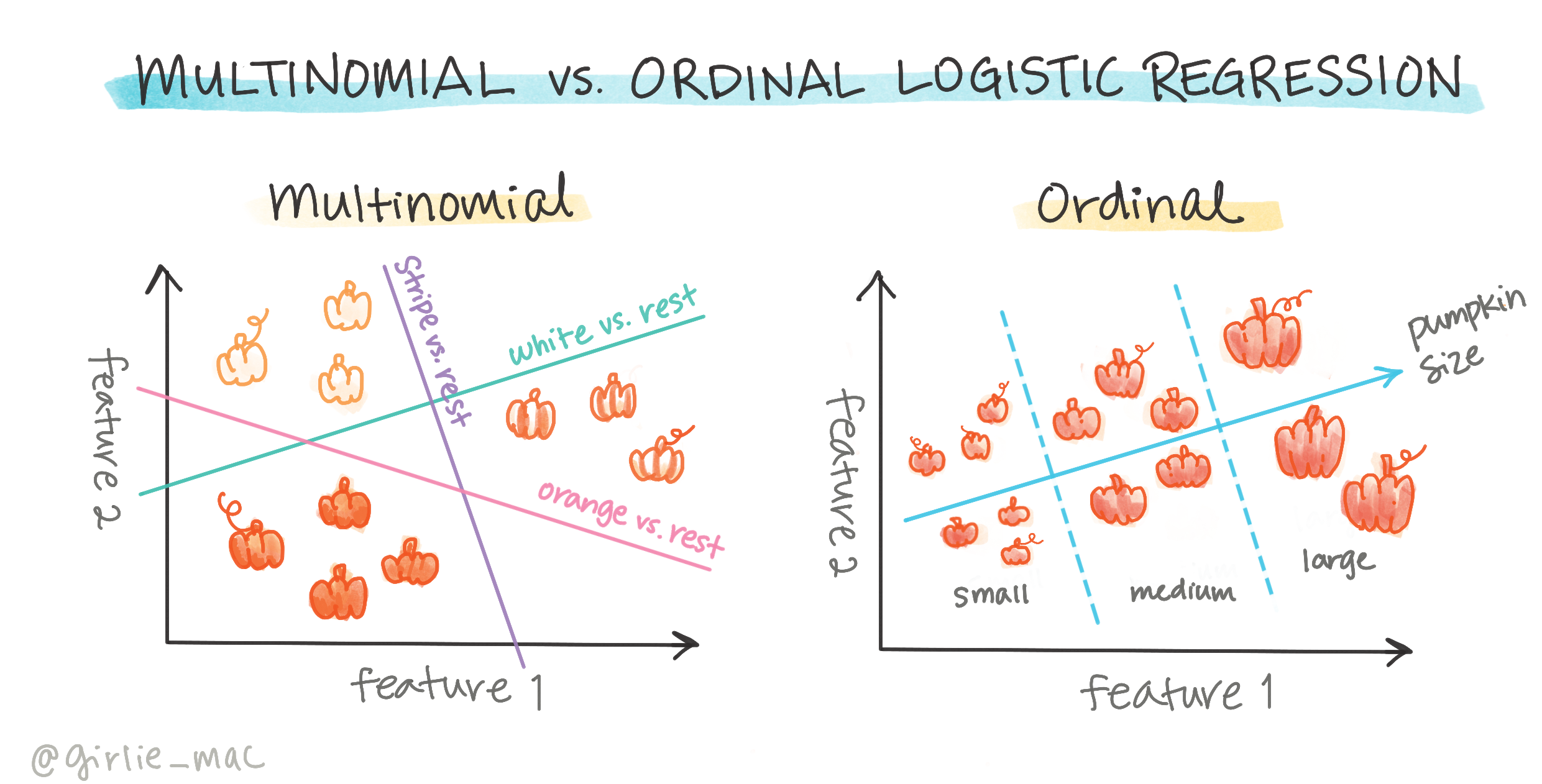
A logisztikus regressziónak vannak más típusai is, például multinomiális és ordinális:

Multinomiális, amely több kategóriát foglal magában - "Narancs, Fehér és Csíkos".
Ordinális, amely rendezett kategóriákat foglal magában, hasznos, ha logikusan szeretnénk rendezni az eredményeket, például a tököket, amelyek egy véges számú méret szerint vannak rendezve (mini, kicsi, közepes, nagy, XL, XXL).

A változóknak NEM kell korrelálniuk

Emlékszel, hogy a lineáris regresszió jobban működött, ha a változók korreláltak? A logisztikus regresszió ennek az ellenkezője - a változóknak nem kell egymáshoz igazodniuk. Ez jól működik az olyan adatokkal, amelyeknek viszonylag gyenge korrelációi vannak.

Sok tiszta adatra van szükség

A logisztikus regresszió pontosabb eredményeket ad, ha több adatot használunk; a mi kis adatállományunk nem optimális erre a feladatra, ezért ezt tartsd szem előtt.

✅ Gondold át, milyen típusú adatok alkalmasak jól a logisztikus regresszióhoz

Gyakorlat - adatok tisztítása

Először tisztítsd meg az adatokat egy kicsit, távolítsd el a null értékeket, és válassz ki csak néhány oszlopot:

Add hozzá a következő kódot:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Mindig megtekintheted az új adatkeretedet:

pumpkins.info

Vizualizáció - kategóriális diagram

Mostanra betöltötted a kezdő notebookot a tökadatokkal, és megtisztítottad úgy, hogy megmaradjon egy adatállomány néhány változóval, beleértve a Color-t. Vizualizáljuk az adatkeretet a notebookban egy másik könyvtár segítségével: Seaborn, amely a korábban használt Matplotlibre épül.

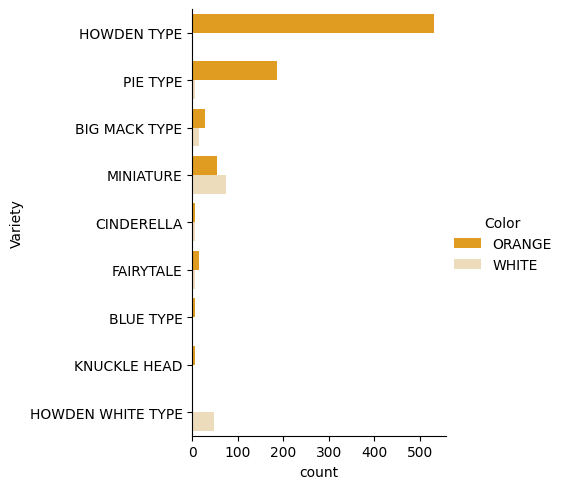
A Seaborn néhány remek módot kínál az adatok vizualizálására. Például összehasonlíthatod az adatok eloszlását a Variety és Color kategóriák szerint egy kategóriális diagramon.

Hozz létre egy ilyen diagramot a catplot függvény használatával, a tökadatainkat (pumpkins) használva, és színkódolást megadva az egyes tökkategóriákhoz (narancs vagy fehér):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Az adatok megfigyelésével láthatod, hogyan kapcsolódik a Color adat a Variety-hez.

✅ Ezen kategóriális diagram alapján milyen érdekes vizsgálatokat tudsz elképzelni?

Adatok előfeldolgozása: jellemzők és címkék kódolása

A tökadataink minden oszlopában szöveges értékek találhatók. A kategóriális adatokkal való munka intuitív az emberek számára, de nem a gépek számára. A gépi tanulási algoritmusok jól működnek számokkal. Ezért a kódolás nagyon fontos lépés az adatok előfeldolgozási fázisában, mivel lehetővé teszi, hogy a kategóriális adatokat numerikus adatokká alakítsuk, anélkül, hogy bármilyen információt elveszítenénk. A jó kódolás jó modell építéséhez vezet.

A jellemzők kódolásához két fő típusú kódoló létezik:

Ordinális kódoló: jól illeszkedik az ordinális változókhoz, amelyek kategóriális változók, ahol az adatok logikai sorrendet követnek, mint például az Item Size oszlop az adatállományunkban. Olyan leképezést hoz létre, amelyben minden kategóriát egy szám képvisel, amely az oszlopban lévő kategória sorrendje.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategóriális kódoló: jól illeszkedik a nominális változókhoz, amelyek kategóriális változók, ahol az adatok nem követnek logikai sorrendet, mint például az adatállományunkban az Item Size-től eltérő összes jellemző. Ez egy one-hot kódolás, ami azt jelenti, hogy minden kategóriát egy bináris oszlop képvisel: a kódolt változó értéke 1, ha a tök az adott Variety-hez tartozik, és 0, ha nem.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Ezután a ColumnTransformer-t használjuk, hogy több kódolót egyetlen lépésben kombináljunk, és alkalmazzuk őket a megfelelő oszlopokra.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Másrészt a címke kódolásához a scikit-learn LabelEncoder osztályát használjuk, amely egy segédosztály, amely segít normalizálni a címkéket úgy, hogy csak 0 és n_classes-1 közötti értékeket tartalmazzanak (itt 0 és 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Miután kódoltuk a jellemzőket és a címkét, egy új adatkeretbe (encoded_pumpkins) egyesíthetjük őket.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Milyen előnyei vannak az ordinális kódoló használatának az Item Size oszlop esetében?

Változók közötti kapcsolatok elemzése

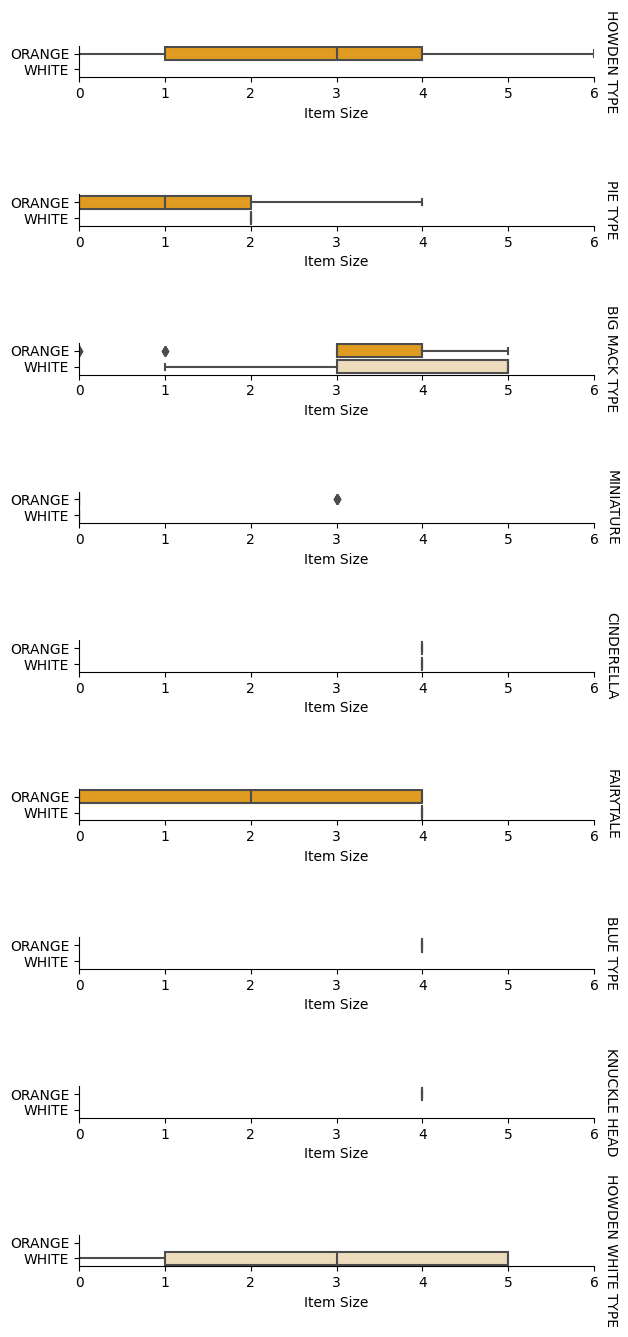
Most, hogy előfeldolgoztuk az adatokat, elemezhetjük a jellemzők és a címke közötti kapcsolatokat, hogy megértsük, mennyire lesz képes a modell előre jelezni a címkét a jellemzők alapján. Az ilyen típusú elemzés legjobb módja az adatok ábrázolása. Ismét a Seaborn catplot függvényét fogjuk használni, hogy vizualizáljuk az Item Size, Variety és Color közötti kapcsolatokat egy kategóriális diagramon. Az adatok jobb ábrázolása érdekében az Item Size kódolt oszlopát és a nem kódolt Variety oszlopot fogjuk használni.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Swarm diagram használata

Mivel a Color egy bináris kategória (Fehér vagy Nem), 'egy speciális megközelítést igényel a vizualizációhoz'. Vannak más módok is, hogy vizualizáljuk ennek a kategóriának a kapcsolatát más változókkal.

A változókat egymás mellett ábrázolhatod Seaborn diagramokkal.

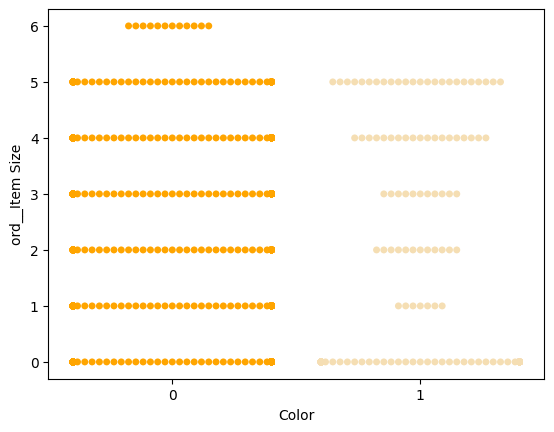
Próbálj ki egy 'swarm' diagramot az értékek eloszlásának megjelenítésére:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Figyelem: a fenti kód figyelmeztetést generálhat, mivel a Seaborn nem tudja megfelelően ábrázolni ilyen mennyiségű adatpontot egy swarm diagramon. Egy lehetséges megoldás a marker méretének csökkentése a 'size' paraméter használatával. Azonban légy tudatában annak, hogy ez befolyásolja a diagram olvashatóságát.

🧮 Mutasd a matematikát

A logisztikus regresszió a 'maximum likelihood' koncepcióján alapul, szigmoid függvények használatával. Egy 'szigmoid függvény' egy grafikonon 'S' alakú görbének tűnik. Egy értéket vesz, és 0 és 1 közé térképezi. A görbéjét 'logisztikus görbének' is nevezik. A képlete így néz ki:

ahol a szigmoid középpontja az x 0 pontján található, L a görbe maximális értéke, és k a görbe meredeksége. Ha a függvény eredménye nagyobb, mint 0.5, az adott címkét a bináris választás '1' osztályába sorolják. Ha nem, akkor '0'-ként osztályozzák.

Építsd fel a modelledet

Egy modell építése ezeknek a bináris osztályozásoknak a megtalálására meglepően egyszerű a Scikit-learn segítségével.

🎥 Kattints a fenti képre egy rövid videós áttekintésért a lineáris regressziós modell építéséről

Válaszd ki azokat a változókat, amelyeket az osztályozási modellben használni szeretnél, és oszd fel a tanulási és tesztkészleteket a train_test_split() hívásával:

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Most már betaníthatod a modelledet a fit() hívásával a tanulási adatokkal, és kiírhatod az eredményét:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Nézd meg a modelled eredménytábláját. Nem rossz, tekintve, hogy csak körülbelül 1000 sor adatod van:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Jobb megértés egy zavaró mátrix segítségével

Bár az eredménytáblát kifejezésekkel is kiírhatod az előző elemek nyomtatásával, könnyebben megértheted a modelledet egy zavaró mátrix használatával, amely segít megérteni, hogyan teljesít a modell.

🎓 A 'zavaró mátrix' (vagy 'hibamátrix') egy táblázat, amely kifejezi a modelled valódi vs. hamis pozitív és negatív értékeit, így mérve az előrejelzések pontosságát.

A zavaró mátrix használatához hívd meg a confusion_matrix() függvényt:

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Nézd meg a modelled zavaró mátrixát:

array([[162,   4],
       [ 11,  22]])

A Scikit-learnben a zavaró mátrix sorai (0. tengely) a valós címkék, míg az oszlopai (1. tengely) az előrejelzett címkék.

	0	1
0	TN	FP
1	FN	TP

Mi történik itt? Tegyük fel, hogy a modelledet arra kérik, hogy osztályozza a tököket két bináris kategória között: 'fehér' és 'nem fehér'.

Ha a modelled nem fehérként jósolja meg a tököt, és az valójában a 'nem fehér' kategóriába tartozik, akkor ezt valódi negatívnak nevezzük, amelyet a bal felső szám mut Hogyan kapcsolódik az összezavarodási mátrix a precizitáshoz és a visszahíváshoz? Ne feledd, a fentebb kinyomtatott osztályozási jelentés megmutatta a precizitást (0.85) és a visszahívást (0.67).

Precizitás = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Visszahívás = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ K: Az összezavarodási mátrix alapján hogyan teljesített a modell? V: Nem rossz; van egy jó számú valódi negatív, de néhány hamis negatív is.

Nézzük meg újra azokat a fogalmakat, amelyeket korábban láttunk, az összezavarodási mátrix TP/TN és FP/FN leképezésének segítségével:

🎓 Precizitás: TP/(TP + FP) Azoknak a releváns példányoknak az aránya, amelyek a visszakeresett példányok között vannak (pl. mely címkék lettek jól címkézve).

🎓 Visszahívás: TP/(TP + FN) Azoknak a releváns példányoknak az aránya, amelyek visszakeresésre kerültek, akár jól címkézve, akár nem.

🎓 f1-pontszám: (2 * precizitás * visszahívás)/(precizitás + visszahívás) A precizitás és visszahívás súlyozott átlaga, ahol a legjobb érték 1, a legrosszabb pedig 0.

🎓 Támogatás: Az egyes visszakeresett címkék előfordulásainak száma.

🎓 Pontosság: (TP + TN)/(TP + TN + FP + FN) Azoknak a címkéknek a százaléka, amelyeket egy mintában pontosan előre jeleztek.

🎓 Makro Átlag: Az egyes címkék súlyozatlan átlagos metrikáinak kiszámítása, figyelmen kívül hagyva a címkék egyensúlyhiányát.

🎓 Súlyozott Átlag: Az egyes címkék átlagos metrikáinak kiszámítása, figyelembe véve a címkék egyensúlyhiányát, azokat a támogatásukkal (az egyes címkék valódi példányainak száma) súlyozva.

✅ Gondolod, hogy melyik metrikát kell figyelned, ha csökkenteni szeretnéd a hamis negatívok számát?

Vizualizáljuk a modell ROC görbéjét

🎥 Kattints a fenti képre egy rövid videós áttekintésért a ROC görbékről

Készítsünk még egy vizualizációt, hogy lássuk az úgynevezett 'ROC' görbét:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

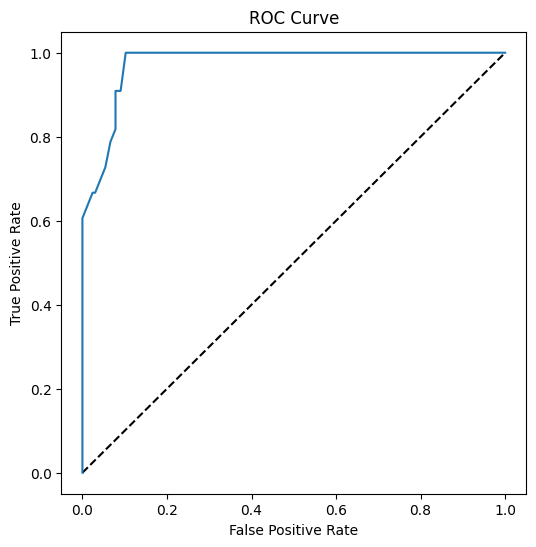
Használjuk a Matplotlibet a modell Receiver Operating Characteristic vagy ROC görbéjének ábrázolására. A ROC görbéket gyakran használják arra, hogy megtekintsék egy osztályozó kimenetét a valódi és hamis pozitívok szempontjából. "A ROC görbék jellemzően a valódi pozitív arányt ábrázolják az Y tengelyen, és a hamis pozitív arányt az X tengelyen." Ezért a görbe meredeksége és a középvonal és a görbe közötti tér számít: olyan görbét szeretnél, amely gyorsan felfelé és a vonal fölé halad. Ebben az esetben vannak kezdeti hamis pozitívok, majd a vonal megfelelően felfelé és fölé halad:

Végül használjuk a Scikit-learn roc_auc_score API-ját az úgynevezett 'Görbe Alatti Terület' (AUC) tényleges kiszámításához:

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Az eredmény 0.9749908725812341. Mivel az AUC 0 és 1 között mozog, magas pontszámot szeretnél, mivel egy modell, amely 100%-ban helyes előrejelzéseket ad, AUC értéke 1 lesz; ebben az esetben a modell elég jó.

A jövőbeli osztályozási leckékben megtanulod, hogyan iterálj a modell pontszámainak javítása érdekében. De most gratulálok! Befejezted ezeket a regressziós leckéket!

🚀Kihívás

Még sok mindent lehet kibontani a logisztikus regresszióval kapcsolatban! De a legjobb módja a tanulásnak az, ha kísérletezel. Keress egy adatállományt, amely alkalmas erre az elemzésre, és építs egy modellt vele. Mit tanulsz? Tipp: próbáld ki a Kaggle oldalt érdekes adatállományokért.

Előadás utáni kvíz

Áttekintés és önálló tanulás

Olvasd el ennek a Stanford-i tanulmánynak az első néhány oldalát a logisztikus regresszió gyakorlati alkalmazásairól. Gondolj olyan feladatokra, amelyek jobban illenek az egyik vagy másik típusú regressziós feladathoz, amelyeket eddig tanulmányoztunk. Mi működne a legjobban?

Feladat

Próbáld újra ezt a regressziót

Felelősség kizárása:
Ez a dokumentum az AI fordítási szolgáltatás, a Co-op Translator segítségével lett lefordítva. Bár törekszünk a pontosságra, kérjük, vegye figyelembe, hogy az automatikus fordítások hibákat vagy pontatlanságokat tartalmazhatnak. Az eredeti dokumentum az eredeti nyelvén tekintendő hiteles forrásnak. Kritikus információk esetén javasolt professzionális emberi fordítást igénybe venni. Nem vállalunk felelősséget semmilyen félreértésért vagy téves értelmezésért, amely a fordítás használatából eredhet.