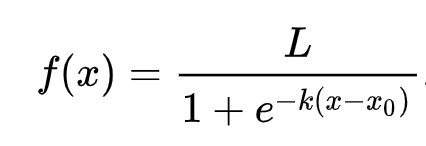History

leestott e4050807fb 🌐 Update translations via Co-op Translator		2 weeks ago
..
solution	🌐 Update translations via Co-op Translator	2 weeks ago
README.md	🌐 Update translations via Co-op Translator	2 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	2 weeks ago
notebook.ipynb	🌐 Update translations via Co-op Translator	3 weeks ago

Logistinen regressio kategorioiden ennustamiseen

Esiluentakysely

Tämä oppitunti on saatavilla myös R-kielellä!

Johdanto

Tässä viimeisessä oppitunnissa regressiosta, joka on yksi perinteisistä klassisen koneoppimisen tekniikoista, tarkastelemme logistista regressiota. Tätä tekniikkaa käytetään mallintamaan ja ennustamaan binäärisiä kategorioita. Onko tämä karkki suklaata vai ei? Onko tämä tauti tarttuva vai ei? Valitseeko asiakas tämän tuotteen vai ei?

Tässä oppitunnissa opit:

Uuden kirjaston datan visualisointiin
Logistisen regression tekniikoita

✅ Syvennä ymmärrystäsi tämän tyyppisestä regressiosta tässä Learn-moduulissa

Esitiedot

Työskenneltyämme kurpitsadataa käyttäen olemme nyt riittävän tuttuja sen kanssa huomataksemme, että siinä on yksi binäärinen kategoria, jonka kanssa voimme työskennellä: Color.

Rakennetaan logistinen regressiomalli ennustamaan, minkä värinen tietty kurpitsa todennäköisesti on (oranssi 🎃 vai valkoinen 👻).

Miksi puhumme binäärisestä luokittelusta regressiota käsittelevässä oppitunnissa? Ainoastaan kielellisen mukavuuden vuoksi, sillä logistinen regressio on todellisuudessa luokittelumenetelmä, vaikkakin lineaarinen sellainen. Opit muista tavoista luokitella dataa seuraavassa oppituntiryhmässä.

Määrittele kysymys

Tässä yhteydessä ilmaisemme tämän binäärisesti: 'Valkoinen' tai 'Ei valkoinen'. Datasetissämme on myös 'raidallinen' kategoria, mutta sen esiintymiä on vähän, joten emme käytä sitä. Se katoaa joka tapauksessa, kun poistamme datasetistä puuttuvat arvot.

🎃 Hauska fakta: kutsumme joskus valkoisia kurpitsoja 'aavekurpitsoiksi'. Niitä ei ole kovin helppo kaivertaa, joten ne eivät ole yhtä suosittuja kuin oranssit, mutta ne näyttävät siisteiltä! Voisimme siis myös muotoilla kysymyksemme näin: 'Aave' vai 'Ei aave'. 👻

Tietoa logistisesta regressiosta

Logistinen regressio eroaa aiemmin oppimastasi lineaarisesta regressiosta muutamalla tärkeällä tavalla.

🎥 Klikkaa yllä olevaa kuvaa saadaksesi lyhyen videoesittelyn logistisesta regressiosta.

Binäärinen luokittelu

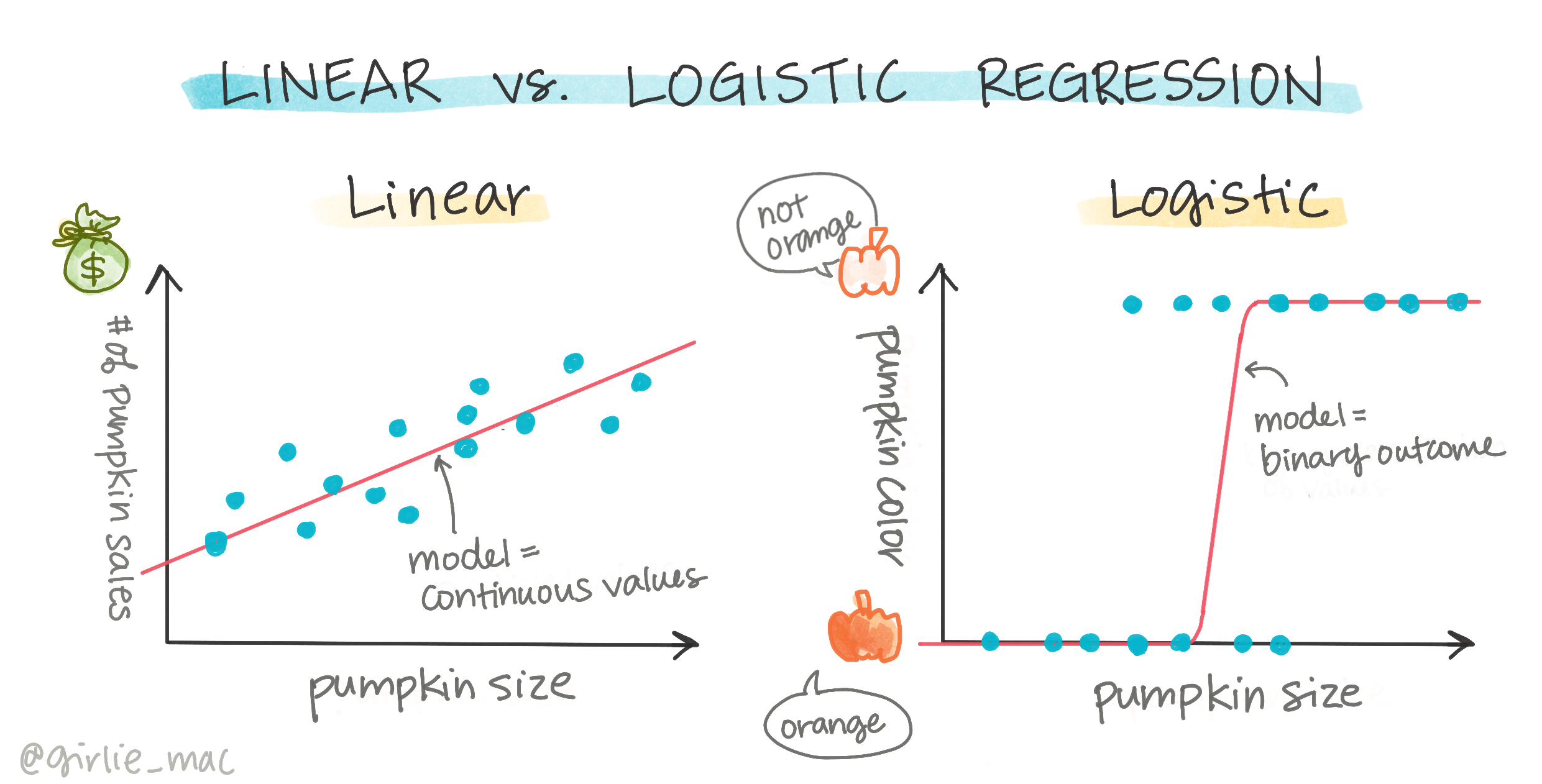
Logistinen regressio ei tarjoa samoja ominaisuuksia kuin lineaarinen regressio. Edellinen tarjoaa ennusteen binäärisestä kategoriasta ("valkoinen tai ei valkoinen"), kun taas jälkimmäinen pystyy ennustamaan jatkuvia arvoja, esimerkiksi kurpitsan alkuperän ja sadonkorjuuajan perusteella, kuinka paljon sen hinta nousee.

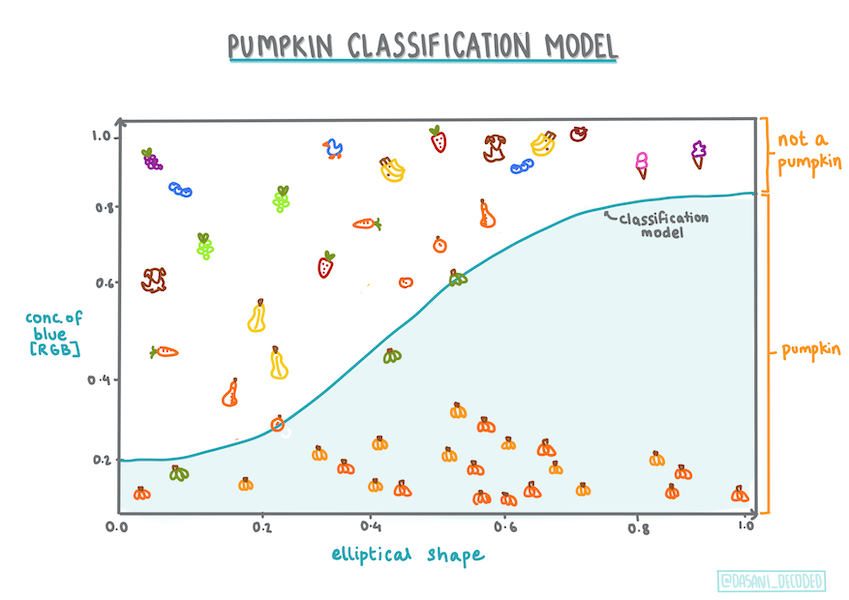
Infografiikka: Dasani Madipalli

Muut luokittelut

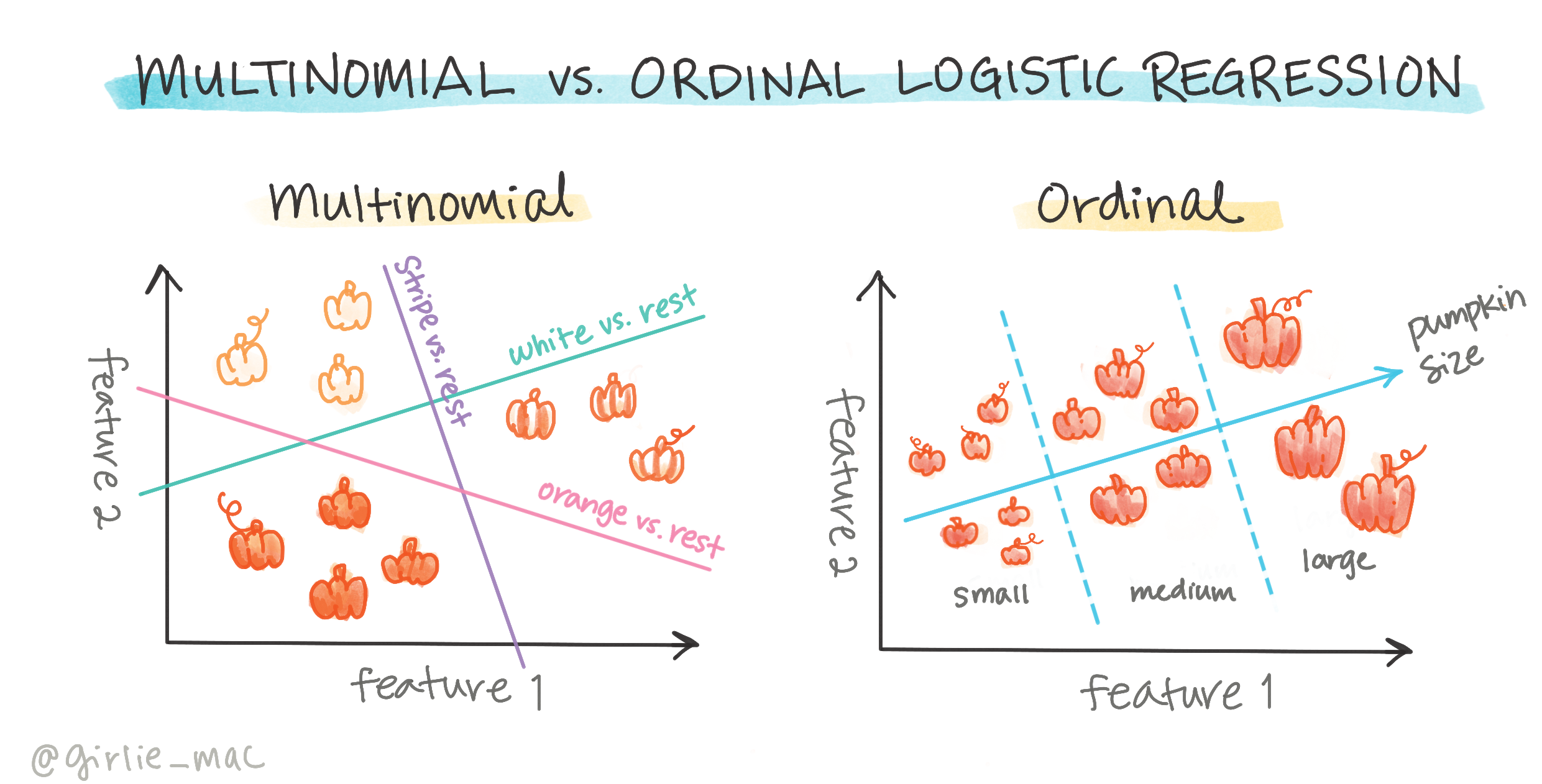
Logistisessa regressiossa on myös muita tyyppejä, kuten multinomiaalinen ja ordinaalinen:

Multinomiaalinen, jossa on useampi kuin yksi kategoria - "Oranssi, Valkoinen ja Raidallinen".
Ordinaalinen, jossa on järjestettyjä kategorioita, hyödyllinen, jos haluamme järjestää tulokset loogisesti, kuten kurpitsat, jotka on järjestetty kokojen mukaan (mini, sm, med, lg, xl, xxl).

Muuttujien EI tarvitse korreloida

Muistatko, kuinka lineaarinen regressio toimi paremmin korreloivien muuttujien kanssa? Logistinen regressio on päinvastainen - muuttujien ei tarvitse olla linjassa. Tämä sopii tälle datalle, jossa korrelaatiot ovat melko heikkoja.

Tarvitset paljon puhdasta dataa

Logistinen regressio antaa tarkempia tuloksia, jos käytät enemmän dataa; pieni datasetimme ei ole optimaalinen tähän tehtävään, joten pidä tämä mielessä.

🎥 Klikkaa yllä olevaa kuvaa saadaksesi lyhyen videoesittelyn datan valmistelusta lineaarista regressiota varten.

✅ Mieti, millaiset datatyypit sopisivat hyvin logistiseen regressioon.

Harjoitus - siivoa data

Ensiksi siivoa dataa hieman, poista puuttuvat arvot ja valitse vain tietyt sarakkeet:

Lisää seuraava koodi:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Voit aina vilkaista uutta dataframeasi:

pumpkins.info

Visualisointi - kategorinen kaavio

Olet nyt ladannut aloitusmuistion kurpitsadatalla ja siivonnut sen niin, että datasetissä on muutama muuttuja, mukaan lukien Color. Visualisoidaan dataframe muistiossa käyttäen eri kirjastoa: Seaborn, joka on rakennettu aiemmin käyttämämme Matplotlibin päälle.

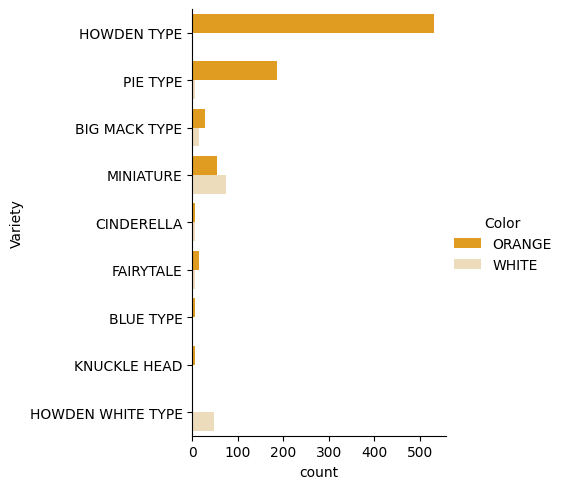
Seaborn tarjoaa käteviä tapoja visualisoida dataa. Esimerkiksi voit verrata datan jakaumia jokaiselle Variety- ja Color-arvolle kategorisessa kaaviossa.

Luo tällainen kaavio käyttämällä catplot-funktiota, käyttäen kurpitsadataamme pumpkins ja määrittämällä värikartta jokaiselle kurpitsakategorialle (oranssi tai valkoinen):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Tarkastelemalla dataa voit nähdä, miten Color-data liittyy Variety-arvoon.

✅ Mitä mielenkiintoisia tutkimusaiheita voit keksiä tämän kategorisen kaavion perusteella?

Datan esikäsittely: ominaisuuksien ja luokkien koodaus

Datasetissämme kaikki sarakkeet sisältävät merkkijonoarvoja. Kategorisen datan käsittely on ihmisille intuitiivista, mutta ei koneille. Koneoppimisalgoritmit toimivat hyvin numeroiden kanssa. Siksi koodaus on erittäin tärkeä vaihe datan esikäsittelyssä, koska se mahdollistaa kategorisen datan muuttamisen numeeriseksi dataksi ilman tietojen menetystä. Hyvä koodaus johtaa hyvän mallin rakentamiseen.

Ominaisuuksien koodaukseen on kaksi päätyyppiä:

Ordinaalikoodaus: sopii hyvin ordinaalisille muuttujille, jotka ovat kategorisia muuttujia, joiden data noudattaa loogista järjestystä, kuten datasetimme Item Size -sarake. Tämä luo kartoituksen, jossa jokainen kategoria esitetään numerolla, joka on sarakkeen kategorian järjestysnumero.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorinen koodaus: sopii hyvin nominaalisille muuttujille, jotka ovat kategorisia muuttujia, joiden data ei noudata loogista järjestystä, kuten kaikki muut datasetin ominaisuudet paitsi Item Size. Tämä on yksi-hot-koodaus, mikä tarkoittaa, että jokainen kategoria esitetään binäärisellä sarakkeella: koodattu muuttuja on yhtä kuin 1, jos kurpitsa kuuluu kyseiseen Variety-arvoon, ja 0 muuten.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Sitten ColumnTransformer-luokkaa käytetään yhdistämään useita koodauksia yhdeksi vaiheeksi ja soveltamaan niitä sopiviin sarakkeisiin.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

Toisaalta luokan koodaamiseen käytämme scikit-learnin LabelEncoder-luokkaa, joka on apuluokka normalisoimaan luokat siten, että ne sisältävät vain arvoja välillä 0 ja n_classes-1 (tässä 0 ja 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Kun olemme koodanneet ominaisuudet ja luokan, voimme yhdistää ne uuteen dataframeen encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Mitkä ovat ordinaalikoodauksen edut Item Size -sarakkeelle?

Analysoi muuttujien välisiä suhteita

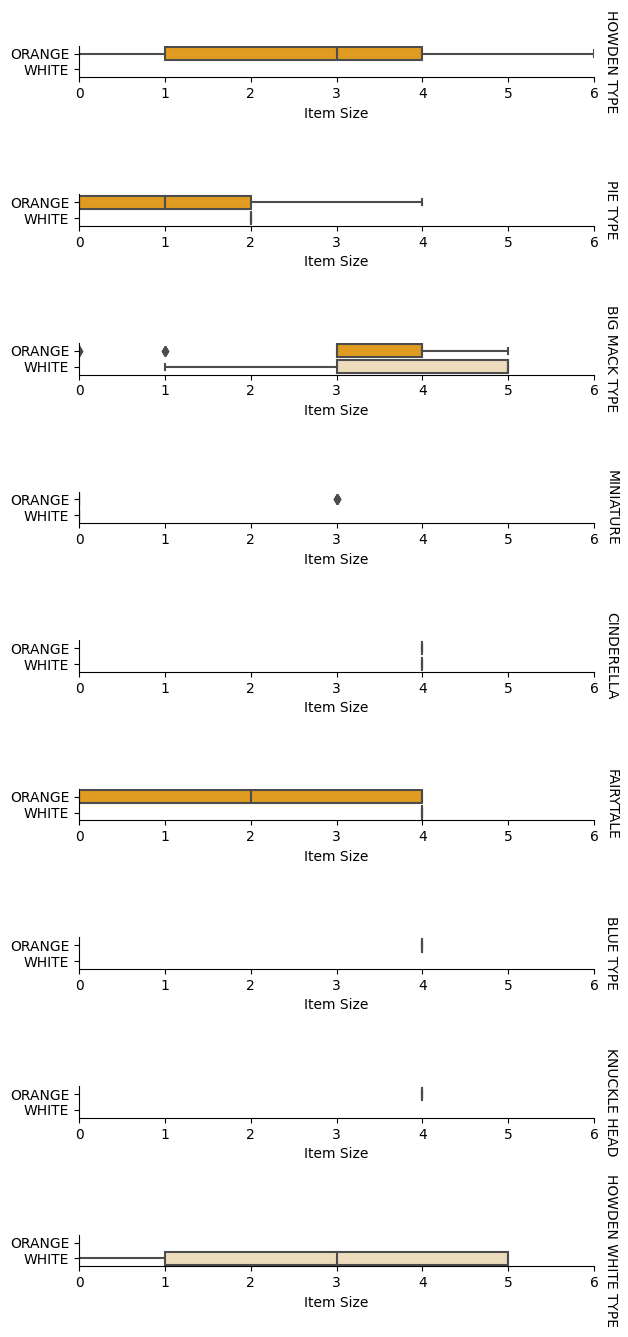
Nyt kun olemme esikäsitelleet datamme, voimme analysoida ominaisuuksien ja luokan välisiä suhteita saadaksemme käsityksen siitä, kuinka hyvin malli pystyy ennustamaan luokan annettujen ominaisuuksien perusteella. Paras tapa suorittaa tämäntyyppinen analyysi on datan visualisointi. Käytämme jälleen Seabornin catplot-funktiota visualisoidaksemme suhteet Item Size-, Variety- ja Color-arvojen välillä kategorisessa kaaviossa. Visualisointia varten käytämme koodattua Item Size -saraketta ja koodaamatonta Variety-saraketta.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Käytä swarm-kaaviota

Koska Color on binäärinen kategoria (valkoinen tai ei), se tarvitsee 'erikoistuneen lähestymistavan' visualisointiin. On olemassa muita tapoja visualisoida tämän kategorian suhde muihin muuttujiin.

Voit visualisoida muuttujia rinnakkain Seabornin kaavioilla.

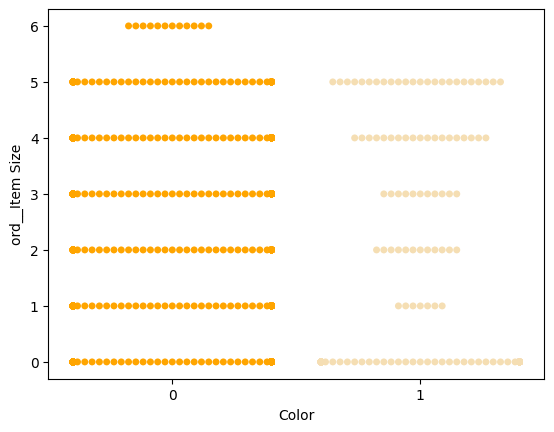
Kokeile 'swarm'-kaaviota arvojen jakauman näyttämiseksi:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Huomio: Yllä oleva koodi saattaa tuottaa varoituksen, koska Seaborn ei pysty esittämään näin suurta määrää datapisteitä swarm-kaaviossa. Mahdollinen ratkaisu on pienentää merkkien kokoa käyttämällä 'size'-parametria. Huomaa kuitenkin, että tämä voi vaikuttaa kaavion luettavuuteen.

🧮 Näytä matematiikka

Logistinen regressio perustuu 'maksimimäärän todennäköisyyden' käsitteeseen käyttäen sigmoidifunktioita. 'Sigmoidifunktio' näyttää graafilla 'S'-muotoiselta. Se ottaa arvon ja muuntaa sen välillä 0 ja 1. Sen käyrää kutsutaan myös 'logistiseksi käyräksi'. Sen kaava näyttää tältä:

missä sigmoidin keskipiste on x:n 0-pisteessä, L on käyrän maksimiarvo ja k on käyrän jyrkkyys. Jos funktion tulos on yli 0,5, kyseinen luokka saa binäärisen valinnan arvon '1'. Muussa tapauksessa se luokitellaan arvoksi '0'.

Rakenna mallisi

Binäärisen luokittelun mallin rakentaminen on yllättävän suoraviivaista Scikit-learnilla.

🎥 Klikkaa yllä olevaa kuvaa saadaksesi lyhyen videoesittelyn logistisen regressiomallin rakentamisesta.

Valitse muuttujat, joita haluat käyttää luokittelumallissasi, ja jaa data koulutus- ja testijoukkoihin kutsumalla train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Nyt voit kouluttaa mallisi kutsumalla fit() koulutusdatalla ja tulostaa sen tuloksen:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Tarkastele mallisi tulostaulukkoa. Se ei ole huono, kun otetaan huomioon, että sinulla on vain noin 1000 riviä dataa:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Parempi ymmärrys virhemaatriksin avulla

Vaikka voit saada tulostaulukon raportin termeistä tulostamalla yllä olevat kohteet, saatat ymmärtää malliasi helpommin käyttämällä virhemaatriksia mallin suorituskyvyn arvioimiseen.

🎓 'Virhemaatriksi' (tai 'virhemaatriksi') on taulukko, joka ilmaisee mallisi todelliset vs. väärät positiiviset ja negatiiviset arvot, ja siten arvioi ennusteiden tarkkuutta.

Käytä virhemaatriksia kutsumalla confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Tarkastele mallisi virhemaatriksia:

array([[162,   4],
       [ 11,  22]])

Scikit-learnissa virhemaatriksin rivit (akseli 0) ovat todellisia luokkia ja sarakkeet (akseli 1) ovat ennustettuja luokkia.

	0	1
0	TN	FP
1	FN	TP

Mitä tässä tapahtuu? Oletetaan, että malliamme pyydetään luokittelemaan kurpitsat kahteen binääriseen kategoriaan, kategoriaan 'valkoinen' ja kategoriaan 'ei-valkoinen'.

Jos mallisi ennustaa kurpitsan ei-valkoiseksi ja se kuuluu todellisuudessa kategoriaan 'ei-valkoinen', kutsumme sitä oikeaksi negatiiviseksi (TN), joka näkyy vasemmassa yläkulmassa.
Jos mallisi ennustaa kurpitsan valkoiseksi ja se kuuluu todellisuudessa kategoriaan 'ei-valkoinen', kutsumme sitä vääräksi positiiviseksi (FP), joka näkyy oikeassa yläkulmassa.
Jos mallisi ennustaa kurpitsan ei-valkoiseksi ja se kuuluu todellisuudessa kategoriaan 'valkoinen', kutsumme sitä vääräksi negatiiviseksi (FN), joka näkyy vasemmassa alakulmassa.
Jos mallisi ennustaa kurpitsan valkoiseksi ja se kuuluu todellisuudessa kategoriaan 'valkoinen', kutsumme sitä oikeaksi positiiviseksi (TP), joka näkyy oikeassa alakulmassa.

Kuten arvata saattaa, on toivottavaa, että oikeiden positiivisten ja oikeiden negatiivisten määrä on suuri ja väärien positiivisten ja väärien negatiivisten määrä pieni, mikä tarkoittaa, että malli toimii paremmin. Miten sekaannusmatriisi liittyy tarkkuuteen ja kattavuuteen? Muista, että yllä tulostettu luokitteluraportti näytti tarkkuuden (0.85) ja kattavuuden (0.67).

Tarkkuus = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Kattavuus = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ K: Miten malli suoriutui sekaannusmatriisin perusteella? V: Ei huono; on hyvä määrä oikeita negatiivisia, mutta myös joitakin vääriä negatiivisia.

Palataan aiemmin nähtyihin termeihin sekaannusmatriisin TP/TN ja FP/FN -kartoituksen avulla:

🎓 Tarkkuus: TP/(TP + FP) Relevanttien tapausten osuus haetuista tapauksista (esim. mitkä tunnisteet merkittiin oikein)

🎓 Kattavuus: TP/(TP + FN) Relevanttien tapausten osuus, jotka haettiin, riippumatta siitä, merkittiinkö ne oikein vai ei

🎓 f1-pisteet: (2 * tarkkuus * kattavuus)/(tarkkuus + kattavuus) Painotettu keskiarvo tarkkuudesta ja kattavuudesta, paras arvo on 1 ja huonoin 0

🎓 Tuki: Haettujen tunnisteiden esiintymien lukumäärä

🎓 Tarkkuus: (TP + TN)/(TP + TN + FP + FN) Oikein ennustettujen tunnisteiden prosenttiosuus näytteestä.

🎓 Makrokeskiarvo: Painottamattomien keskiarvojen laskeminen kullekin tunnisteelle, ottamatta huomioon tunnisteiden epätasapainoa.

🎓 Painotettu keskiarvo: Keskiarvojen laskeminen kullekin tunnisteelle, ottaen huomioon tunnisteiden epätasapaino painottamalla niitä niiden tuen (kunkin tunnisteen oikeiden tapausten lukumäärän) mukaan.

✅ Voitko miettiä, mitä metriikkaa sinun tulisi seurata, jos haluat vähentää väärien negatiivisten määrää?

Visualisoi tämän mallin ROC-käyrä

🎥 Klikkaa yllä olevaa kuvaa saadaksesi lyhyen videokatsauksen ROC-käyristä

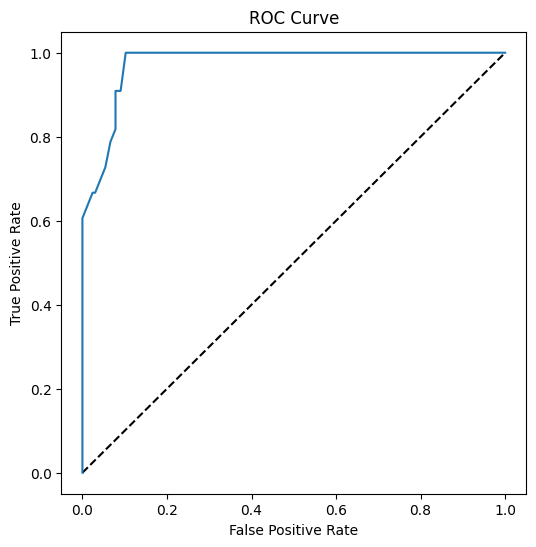
Tehdään vielä yksi visualisointi, jotta näemme niin sanotun 'ROC'-käyrän:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

Käyttämällä Matplotlibia, piirrä mallin Receiving Operating Characteristic eli ROC. ROC-käyriä käytetään usein luokittelijan tulosten tarkasteluun oikeiden ja väärien positiivisten osalta. "ROC-käyrillä Y-akselilla on yleensä oikeiden positiivisten osuus ja X-akselilla väärien positiivisten osuus." Käyrän jyrkkyys ja väli keskilinjan ja käyrän välillä ovat tärkeitä: haluat käyrän, joka nopeasti nousee ja menee linjan yli. Meidän tapauksessamme on aluksi vääriä positiivisia, ja sitten linja nousee ja menee kunnolla yli:

Lopuksi, käytä Scikit-learnin roc_auc_score APIa laskeaksesi todellinen 'Area Under the Curve' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Tulos on 0.9749908725812341. Koska AUC vaihtelee välillä 0–1, haluat korkean pistemäärän, sillä malli, joka on 100 % oikeassa ennusteissaan, saa AUC-arvon 1; tässä tapauksessa malli on melko hyvä.

Tulevissa luokitteluun liittyvissä oppitunneissa opit, kuinka voit parantaa mallisi pisteitä iteratiivisesti. Mutta nyt, onneksi olkoon! Olet suorittanut nämä regressio-oppitunnit!

🚀Haaste

Logistiseen regressioon liittyy paljon enemmän! Mutta paras tapa oppia on kokeilla. Etsi datasetti, joka sopii tämän tyyppiseen analyysiin, ja rakenna malli sen avulla. Mitä opit? vinkki: kokeile Kagglea löytääksesi mielenkiintoisia datasettejä.

Luennon jälkeinen kysely

Kertaus & Itseopiskelu

Lue tämän Stanfordin artikkelin ensimmäiset sivut logistisen regression käytännön sovelluksista. Mieti tehtäviä, jotka sopivat paremmin jommallekummalle regressiotyypille, joita olemme tähän mennessä opiskelleet. Mikä toimisi parhaiten?

Tehtävä

Uudelleen yrittäminen tässä regressiossa

Vastuuvapauslauseke:
Tämä asiakirja on käännetty käyttämällä tekoälypohjaista käännöspalvelua Co-op Translator. Vaikka pyrimme tarkkuuteen, huomioithan, että automaattiset käännökset voivat sisältää virheitä tai epätarkkuuksia. Alkuperäinen asiakirja sen alkuperäisellä kielellä tulisi pitää ensisijaisena lähteenä. Kriittisen tiedon osalta suositellaan ammattimaista ihmiskäännöstä. Emme ole vastuussa väärinkäsityksistä tai virhetulkinnoista, jotka johtuvat tämän käännöksen käytöstä.

README.md Unescape Escape