|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 2 weeks ago | |
| working | 2 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.md | 2 weeks ago | |
README.md
Introduktion til tidsserieforudsigelse
Sketchnote af Tomomi Imura
I denne lektion og den næste vil du lære lidt om tidsserieforudsigelse, en interessant og værdifuld del af en ML-forskers repertoire, som er lidt mindre kendt end andre emner. Tidsserieforudsigelse er en slags 'krystalkugle': baseret på tidligere præstationer af en variabel, såsom pris, kan du forudsige dens fremtidige potentielle værdi.
🎥 Klik på billedet ovenfor for en video om tidsserieforudsigelse
Quiz før lektionen
Det er et nyttigt og interessant felt med reel værdi for erhvervslivet, givet dets direkte anvendelse på problemer som prissætning, lagerbeholdning og forsyningskædeproblemer. Selvom dyb læringsteknikker er begyndt at blive brugt til at opnå flere indsigter for bedre at forudsige fremtidige præstationer, forbliver tidsserieforudsigelse et felt, der i høj grad er informeret af klassiske ML-teknikker.
Penn States nyttige tidsseriecurriculum kan findes her
Introduktion
Forestil dig, at du vedligeholder en række smarte parkeringsmålere, der giver data om, hvor ofte de bruges, og hvor længe over tid.
Hvad hvis du kunne forudsige, baseret på målerens tidligere præstationer, dens fremtidige værdi i henhold til udbud og efterspørgsel?
At forudsige præcist, hvornår man skal handle for at opnå sit mål, er en udfordring, der kunne tackles med tidsserieforudsigelse. Det ville ikke gøre folk glade at blive opkrævet mere i travle perioder, når de leder efter en parkeringsplads, men det ville være en sikker måde at generere indtægter til at rengøre gaderne!
Lad os udforske nogle af typerne af tidsseriealgoritmer og starte en notebook for at rense og forberede nogle data. De data, du vil analysere, er taget fra GEFCom2014-forudsigelseskonkurrencen. Det består af 3 års timelige elforbrug og temperaturværdier mellem 2012 og 2014. Givet de historiske mønstre for elforbrug og temperatur kan du forudsige fremtidige værdier for elforbrug.
I dette eksempel vil du lære, hvordan man forudsiger ét tidssteg fremad ved kun at bruge historiske forbrugsdata. Før du starter, er det dog nyttigt at forstå, hvad der foregår bag kulisserne.
Nogle definitioner
Når du støder på begrebet 'tidsserie', skal du forstå dets anvendelse i flere forskellige sammenhænge.
🎓 Tidsserie
I matematik er "en tidsserie en række datapunkter indekseret (eller listet eller grafet) i tidsorden. Oftest er en tidsserie en sekvens taget på successive lige store punkter i tid." Et eksempel på en tidsserie er den daglige lukningsværdi af Dow Jones Industrial Average. Brug af tidsserieplots og statistisk modellering ses ofte i signalbehandling, vejrforudsigelse, jordskælvforudsigelse og andre felter, hvor begivenheder opstår, og datapunkter kan plottes over tid.
🎓 Tidsserieanalyse
Tidsserieanalyse er analysen af ovennævnte tidsseriedata. Tidsseriedata kan tage forskellige former, herunder 'afbrudte tidsserier', som opdager mønstre i en tidsseries udvikling før og efter en afbrydende begivenhed. Den type analyse, der er nødvendig for tidsserien, afhænger af dataens natur. Tidsseriedata kan selv tage form af serier af tal eller tegn.
Analysen, der skal udføres, bruger en række metoder, herunder frekvensdomæne og tidsdomæne, lineær og ikke-lineær og mere. Lær mere om de mange måder at analysere denne type data på.
🎓 Tidsserieforudsigelse
Tidsserieforudsigelse er brugen af en model til at forudsige fremtidige værdier baseret på mønstre vist af tidligere indsamlede data, som de opstod i fortiden. Selvom det er muligt at bruge regressionsmodeller til at udforske tidsseriedata, med tidsindekser som x-variabler på et plot, analyseres sådanne data bedst ved hjælp af specielle typer modeller.
Tidsseriedata er en liste over ordnede observationer, i modsætning til data, der kan analyseres ved lineær regression. Den mest almindelige er ARIMA, et akronym, der står for "Autoregressive Integrated Moving Average".
ARIMA-modeller "relaterer den nuværende værdi af en serie til tidligere værdier og tidligere forudsigelsesfejl." De er mest passende til at analysere tidsdomænedata, hvor data er ordnet over tid.
Der er flere typer ARIMA-modeller, som du kan lære om her, og som du vil berøre i den næste lektion.
I den næste lektion vil du bygge en ARIMA-model ved hjælp af Univariate Time Series, som fokuserer på én variabel, der ændrer sin værdi over tid. Et eksempel på denne type data er dette datasæt, der registrerer den månedlige CO2-koncentration ved Mauna Loa-observatoriet:
| CO2 | YearMonth | Year | Month |
|---|---|---|---|
| 330.62 | 1975.04 | 1975 | 1 |
| 331.40 | 1975.13 | 1975 | 2 |
| 331.87 | 1975.21 | 1975 | 3 |
| 333.18 | 1975.29 | 1975 | 4 |
| 333.92 | 1975.38 | 1975 | 5 |
| 333.43 | 1975.46 | 1975 | 6 |
| 331.85 | 1975.54 | 1975 | 7 |
| 330.01 | 1975.63 | 1975 | 8 |
| 328.51 | 1975.71 | 1975 | 9 |
| 328.41 | 1975.79 | 1975 | 10 |
| 329.25 | 1975.88 | 1975 | 11 |
| 330.97 | 1975.96 | 1975 | 12 |
✅ Identificer den variabel, der ændrer sig over tid i dette datasæt
Tidsseriedatas karakteristika, der skal overvejes
Når du ser på tidsseriedata, kan du bemærke, at det har visse karakteristika, som du skal tage højde for og afhjælpe for bedre at forstå dets mønstre. Hvis du betragter tidsseriedata som potentielt leverende et 'signal', som du vil analysere, kan disse karakteristika betragtes som 'støj'. Du vil ofte have brug for at reducere denne 'støj' ved at afhjælpe nogle af disse karakteristika ved hjælp af statistiske teknikker.
Her er nogle begreber, du bør kende for at kunne arbejde med tidsserier:
🎓 Trends
Trends defineres som målbare stigninger og fald over tid. Læs mere. I konteksten af tidsserier handler det om, hvordan man bruger og, hvis nødvendigt, fjerner trends fra din tidsserie.
Sæsonvariation defineres som periodiske udsving, såsom julehandlen, der kan påvirke salget. Tag et kig på, hvordan forskellige typer plots viser sæsonvariation i data.
🎓 Udkast
Udkast er datapunkter, der ligger langt fra den normale datavarians.
🎓 Langsigtet cyklus
Uafhængigt af sæsonvariation kan data vise en langsigtet cyklus, såsom en økonomisk nedgang, der varer længere end et år.
🎓 Konstant varians
Over tid viser nogle data konstante udsving, såsom energiforbrug dag og nat.
🎓 Pludselige ændringer
Data kan vise en pludselig ændring, der kræver yderligere analyse. Den pludselige lukning af virksomheder på grund af COVID, for eksempel, forårsagede ændringer i data.
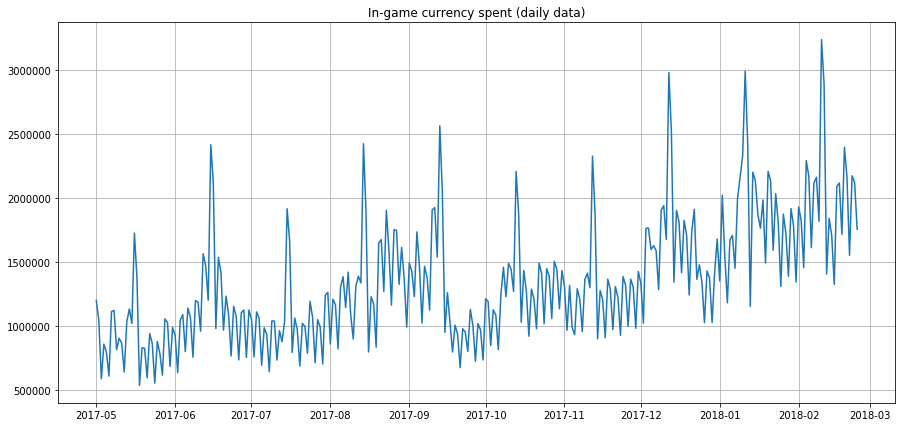
✅ Her er et eksempel på et tidsserieplot, der viser dagligt forbrug af in-game valuta over nogle år. Kan du identificere nogle af de karakteristika, der er nævnt ovenfor, i disse data?
Øvelse - kom i gang med data om energiforbrug
Lad os komme i gang med at oprette en tidsseriemodel for at forudsige fremtidigt energiforbrug baseret på tidligere forbrug.
Dataene i dette eksempel er taget fra GEFCom2014-forudsigelseskonkurrencen. Det består af 3 års timelige elforbrug og temperaturværdier mellem 2012 og 2014.
Tao Hong, Pierre Pinson, Shu Fan, Hamidreza Zareipour, Alberto Troccoli og Rob J. Hyndman, "Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond", International Journal of Forecasting, vol.32, no.3, pp 896-913, juli-september, 2016.
-
I
working-mappen for denne lektion, åbn notebook.ipynb-filen. Start med at tilføje biblioteker, der vil hjælpe dig med at indlæse og visualisere dataimport os import matplotlib.pyplot as plt from common.utils import load_data %matplotlib inlineBemærk, at du bruger filerne fra den medfølgende
common-mappe, som opsætter dit miljø og håndterer download af data. -
Undersøg derefter dataene som en dataframe ved at kalde
load_data()oghead():data_dir = './data' energy = load_data(data_dir)[['load']] energy.head()Du kan se, at der er to kolonner, der repræsenterer dato og forbrug:
load 2012-01-01 00:00:00 2698.0 2012-01-01 01:00:00 2558.0 2012-01-01 02:00:00 2444.0 2012-01-01 03:00:00 2402.0 2012-01-01 04:00:00 2403.0 -
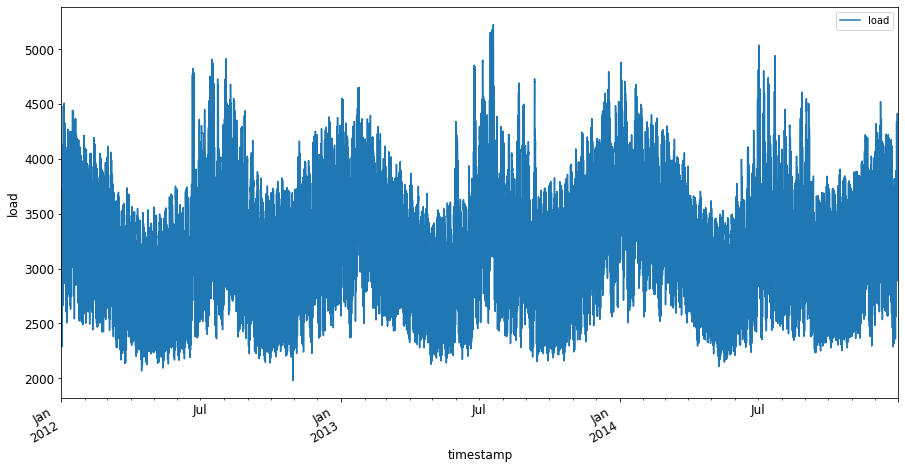
Nu, plot dataene ved at kalde
plot():energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12) plt.xlabel('timestamp', fontsize=12) plt.ylabel('load', fontsize=12) plt.show() -
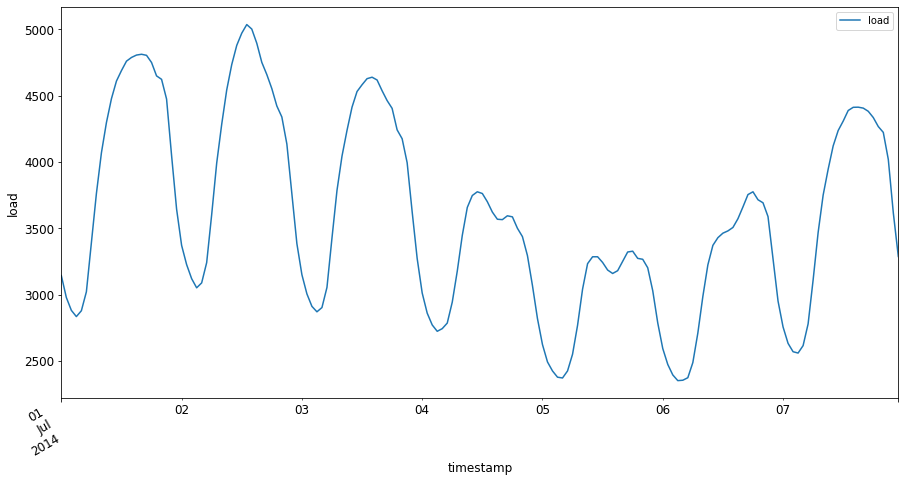
Nu, plot den første uge af juli 2014 ved at angive den som input til
energyi[fra dato]: [til dato]-mønsteret:energy['2014-07-01':'2014-07-07'].plot(y='load', subplots=True, figsize=(15, 8), fontsize=12) plt.xlabel('timestamp', fontsize=12) plt.ylabel('load', fontsize=12) plt.show()Et smukt plot! Tag et kig på disse plots og se, om du kan bestemme nogle af de karakteristika, der er nævnt ovenfor. Hvad kan vi udlede ved at visualisere dataene?
I den næste lektion vil du oprette en ARIMA-model for at lave nogle forudsigelser.
🚀Udfordring
Lav en liste over alle de industrier og områder, du kan komme i tanke om, der ville drage fordel af tidsserieforudsigelse. Kan du tænke på en anvendelse af disse teknikker inden for kunst? Inden for økonometrik? Økologi? Detailhandel? Industri? Finans? Hvor ellers?
Quiz efter lektionen
Gennemgang & Selvstudie
Selvom vi ikke dækker dem her, bruges neurale netværk nogle gange til at forbedre klassiske metoder til tidsserieforudsigelse. Læs mere om dem i denne artikel
Opgave
Ansvarsfraskrivelse:
Dette dokument er blevet oversat ved hjælp af AI-oversættelsestjenesten Co-op Translator. Selvom vi bestræber os på nøjagtighed, skal du være opmærksom på, at automatiserede oversættelser kan indeholde fejl eller unøjagtigheder. Det originale dokument på dets oprindelige sprog bør betragtes som den autoritative kilde. For kritisk information anbefales professionel menneskelig oversættelse. Vi er ikke ansvarlige for eventuelle misforståelser eller fejltolkninger, der opstår som følge af brugen af denne oversættelse.