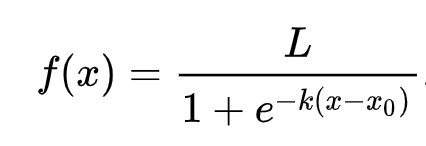History

leestott e4050807fb 🌐 Update translations via Co-op Translator		2 weeks ago
..
solution	🌐 Update translations via Co-op Translator	2 weeks ago
README.md	🌐 Update translations via Co-op Translator	2 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	2 weeks ago
notebook.ipynb	🌐 Update translations via Co-op Translator	3 weeks ago

README.md

Logistisk regression til at forudsige kategorier

Quiz før lektionen

Denne lektion er tilgængelig i R!

Introduktion

I denne sidste lektion om regression, en af de grundlæggende klassiske ML-teknikker, vil vi se nærmere på logistisk regression. Du kan bruge denne teknik til at finde mønstre og forudsige binære kategorier. Er dette slik chokolade eller ej? Er denne sygdom smitsom eller ej? Vil denne kunde vælge dette produkt eller ej?

I denne lektion vil du lære:

Et nyt bibliotek til datavisualisering
Teknikker til logistisk regression

✅ Uddyb din forståelse af at arbejde med denne type regression i dette Learn-modul

Forudsætning

Efter at have arbejdet med græskardataene er vi nu tilstrækkeligt bekendte med dem til at indse, at der er én binær kategori, vi kan arbejde med: Color.

Lad os bygge en logistisk regressionsmodel for at forudsige, givet nogle variabler, hvilken farve et givet græskar sandsynligvis har (orange 🎃 eller hvid 👻).

Hvorfor taler vi om binær klassifikation i en lektion om regression? Kun af sproglig bekvemmelighed, da logistisk regression faktisk er en klassifikationsmetode, omend en lineær-baseret en. Lær om andre måder at klassificere data på i den næste lektion.

Definer spørgsmålet

For vores formål vil vi udtrykke dette som en binær: 'Hvid' eller 'Ikke hvid'. Der er også en 'stribet' kategori i vores datasæt, men der er få forekomster af den, så vi vil ikke bruge den. Den forsvinder alligevel, når vi fjerner null-værdier fra datasættet.

🎃 Sjov fakta: Vi kalder nogle gange hvide græskar for 'spøgelsesgræskar'. De er ikke særlig nemme at skære i, så de er ikke lige så populære som de orange, men de ser seje ud! Så vi kunne også omformulere vores spørgsmål som: 'Spøgelse' eller 'Ikke spøgelse'. 👻

Om logistisk regression

Logistisk regression adskiller sig fra lineær regression, som du tidligere har lært om, på nogle vigtige måder.

🎥 Klik på billedet ovenfor for en kort videooversigt over logistisk regression.

Binær klassifikation

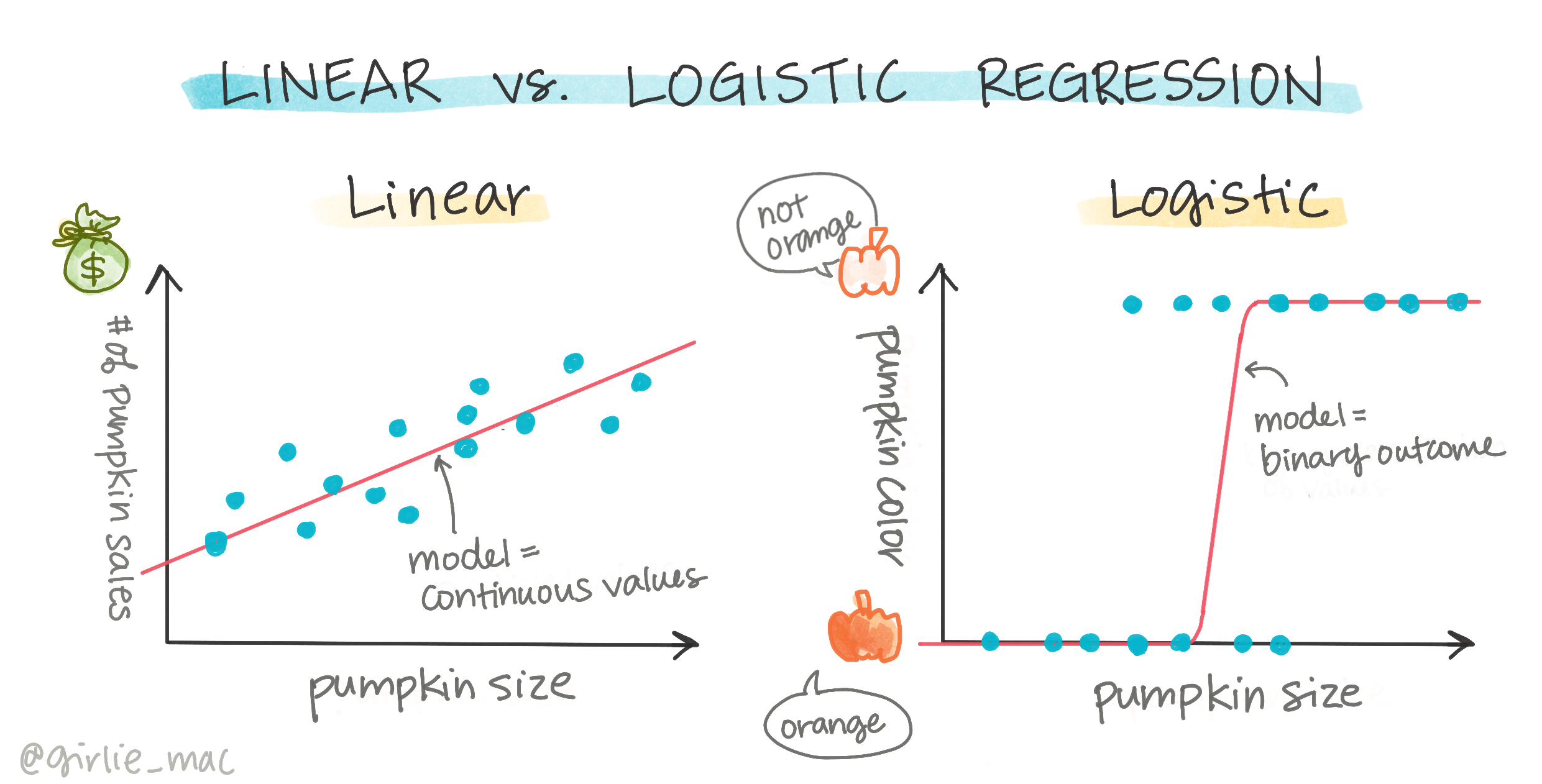
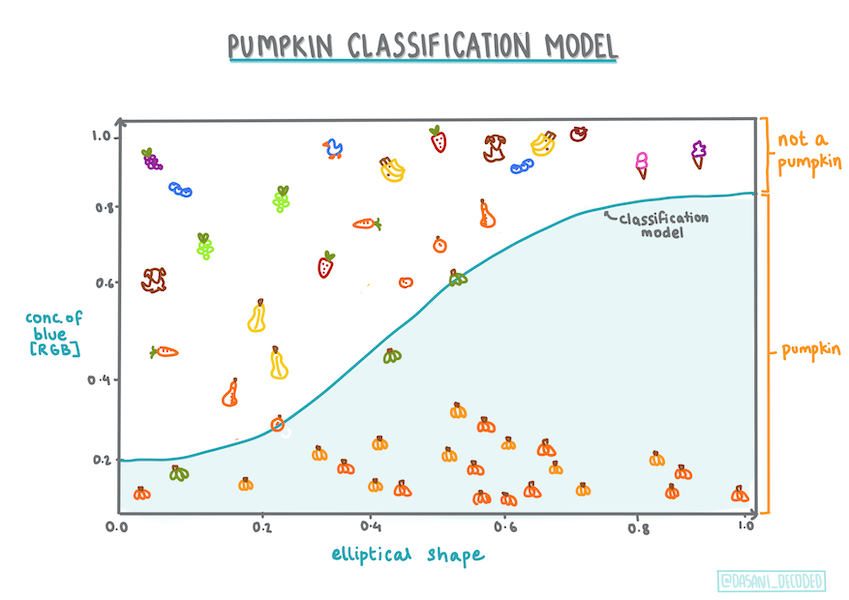
Logistisk regression tilbyder ikke de samme funktioner som lineær regression. Den førstnævnte giver en forudsigelse om en binær kategori ("hvid eller ikke hvid"), mens den sidstnævnte er i stand til at forudsige kontinuerlige værdier, for eksempel givet oprindelsen af et græskar og tidspunktet for høsten, hvor meget prisen vil stige.

Infografik af Dasani Madipalli

Andre klassifikationer

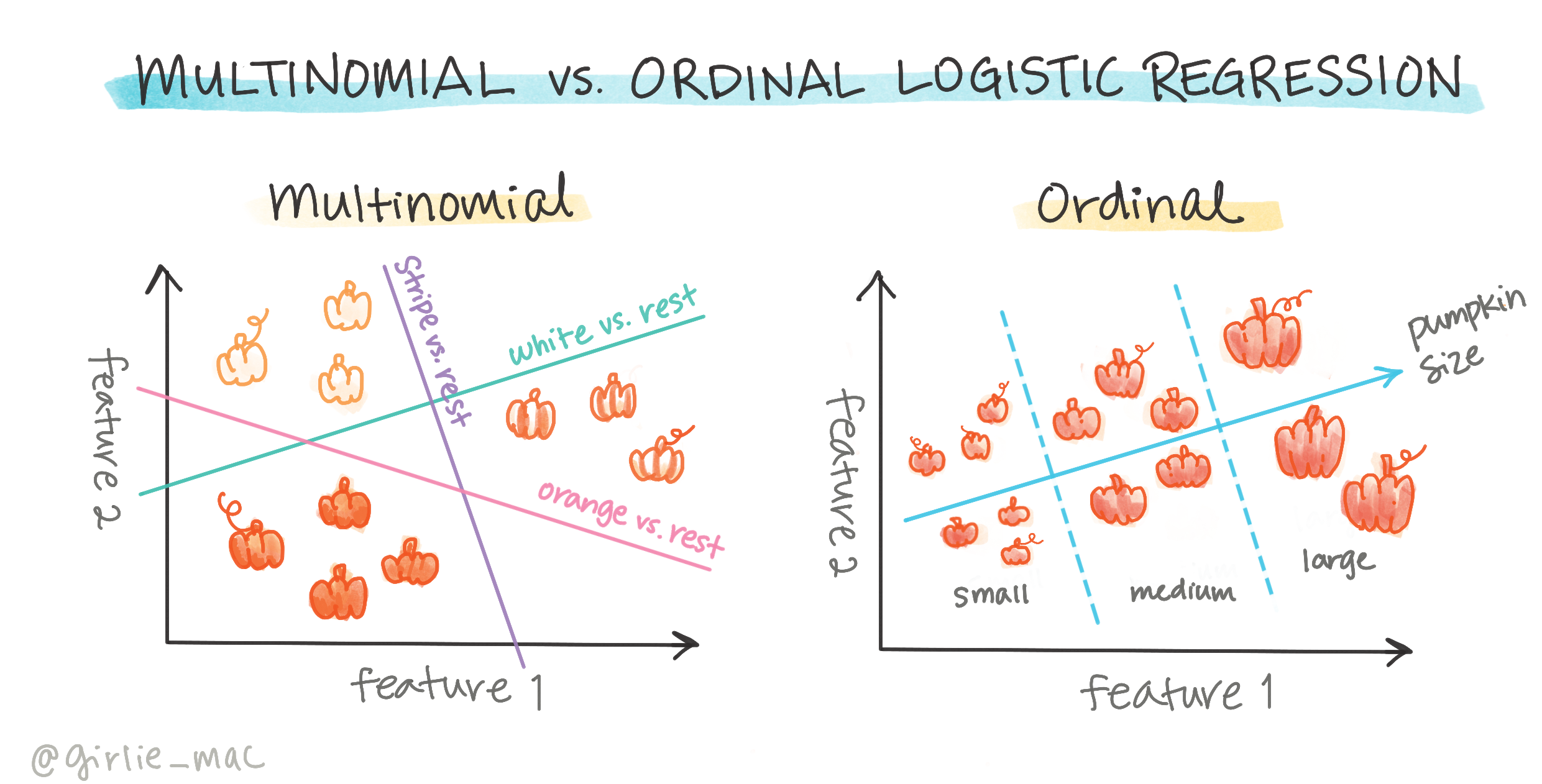
Der findes andre typer logistisk regression, herunder multinomial og ordinal:

Multinomial, som involverer mere end én kategori - "Orange, Hvid og Stribet".
Ordinal, som involverer ordnede kategorier, nyttigt hvis vi ønskede at ordne vores resultater logisk, som vores græskar, der er ordnet efter et begrænset antal størrelser (mini, sm, med, lg, xl, xxl).

Variabler behøver IKKE at korrelere

Kan du huske, hvordan lineær regression fungerede bedre med mere korrelerede variabler? Logistisk regression er det modsatte - variablerne behøver ikke at være i overensstemmelse. Det fungerer for disse data, som har noget svage korrelationer.

Du har brug for mange rene data

Logistisk regression giver mere præcise resultater, hvis du bruger flere data; vores lille datasæt er ikke optimalt til denne opgave, så husk det.

🎥 Klik på billedet ovenfor for en kort videooversigt over forberedelse af data til lineær regression

✅ Tænk over, hvilke typer data der egner sig godt til logistisk regression

Øvelse - ryd op i dataene

Først skal du rydde lidt op i dataene ved at fjerne null-værdier og vælge kun nogle af kolonnerne:

Tilføj følgende kode:


columns_to_select = ['City Name','Package','Variety', 'Origin','Item Size', 'Color']
pumpkins = full_pumpkins.loc[:, columns_to_select]

pumpkins.dropna(inplace=True)

Du kan altid tage et kig på din nye dataframe:

pumpkins.info

Visualisering - kategorisk plot

Nu har du indlæst start-notebooken med græskardata igen og ryddet op i den, så du har et datasæt, der indeholder nogle få variabler, inklusive Color. Lad os visualisere dataframen i notebooken ved hjælp af et andet bibliotek: Seaborn, som er bygget på Matplotlib, som vi brugte tidligere.

Seaborn tilbyder nogle smarte måder at visualisere dine data på. For eksempel kan du sammenligne fordelingen af dataene for hver Variety og Color i et kategorisk plot.

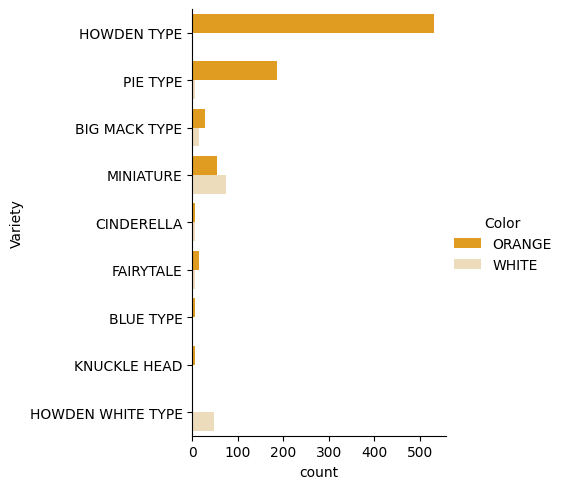
Opret et sådant plot ved hjælp af funktionen catplot, brug vores græskardata pumpkins, og angiv en farvekodning for hver græskarkategori (orange eller hvid):
```
import seaborn as sns

palette = {
'ORANGE': 'orange',
'WHITE': 'wheat',
}

sns.catplot(
data=pumpkins, y="Variety", hue="Color", kind="count",
palette=palette, 
)
```
Ved at observere dataene kan du se, hvordan Color relaterer sig til Variety.

✅ Givet dette kategoriske plot, hvilke interessante undersøgelser kan du forestille dig?

Databehandling: feature- og labelkodning

Vores græskardatasæt indeholder strengværdier for alle dets kolonner. At arbejde med kategoriske data er intuitivt for mennesker, men ikke for maskiner. Maskinlæringsalgoritmer fungerer godt med tal. Derfor er kodning et meget vigtigt trin i databehandlingsfasen, da det gør det muligt for os at omdanne kategoriske data til numeriske data uden at miste nogen information. God kodning fører til opbygning af en god model.

For feature-kodning er der to hovedtyper af kodere:

Ordinal encoder: Den passer godt til ordinale variabler, som er kategoriske variabler, hvor deres data følger en logisk rækkefølge, som kolonnen Item Size i vores datasæt. Den opretter en mapping, så hver kategori repræsenteres af et tal, som er rækkefølgen af kategorien i kolonnen.
```
from sklearn.preprocessing import OrdinalEncoder

item_size_categories = [['sml', 'med', 'med-lge', 'lge', 'xlge', 'jbo', 'exjbo']]
ordinal_features = ['Item Size']
ordinal_encoder = OrdinalEncoder(categories=item_size_categories)
```
Kategorisk encoder: Den passer godt til nominelle variabler, som er kategoriske variabler, hvor deres data ikke følger en logisk rækkefølge, som alle funktionerne bortset fra Item Size i vores datasæt. Det er en one-hot encoding, hvilket betyder, at hver kategori repræsenteres af en binær kolonne: den kodede variabel er lig med 1, hvis græskarret tilhører den Variety og 0 ellers.
```
from sklearn.preprocessing import OneHotEncoder

categorical_features = ['City Name', 'Package', 'Variety', 'Origin']
categorical_encoder = OneHotEncoder(sparse_output=False)
```

Derefter bruges ColumnTransformer til at kombinere flere kodere i et enkelt trin og anvende dem på de relevante kolonner.

    from sklearn.compose import ColumnTransformer
    
    ct = ColumnTransformer(transformers=[
        ('ord', ordinal_encoder, ordinal_features),
        ('cat', categorical_encoder, categorical_features)
        ])
    
    ct.set_output(transform='pandas')
    encoded_features = ct.fit_transform(pumpkins)

For at kode labelen bruger vi scikit-learn-klassen LabelEncoder, som er en hjælpeklasse til at normalisere labels, så de kun indeholder værdier mellem 0 og n_classes-1 (her, 0 og 1).

    from sklearn.preprocessing import LabelEncoder

    label_encoder = LabelEncoder()
    encoded_label = label_encoder.fit_transform(pumpkins['Color'])

Når vi har kodet funktionerne og labelen, kan vi flette dem til en ny dataframe encoded_pumpkins.

    encoded_pumpkins = encoded_features.assign(Color=encoded_label)

✅ Hvad er fordelene ved at bruge en ordinal encoder til kolonnen Item Size?

Analyser forholdet mellem variabler

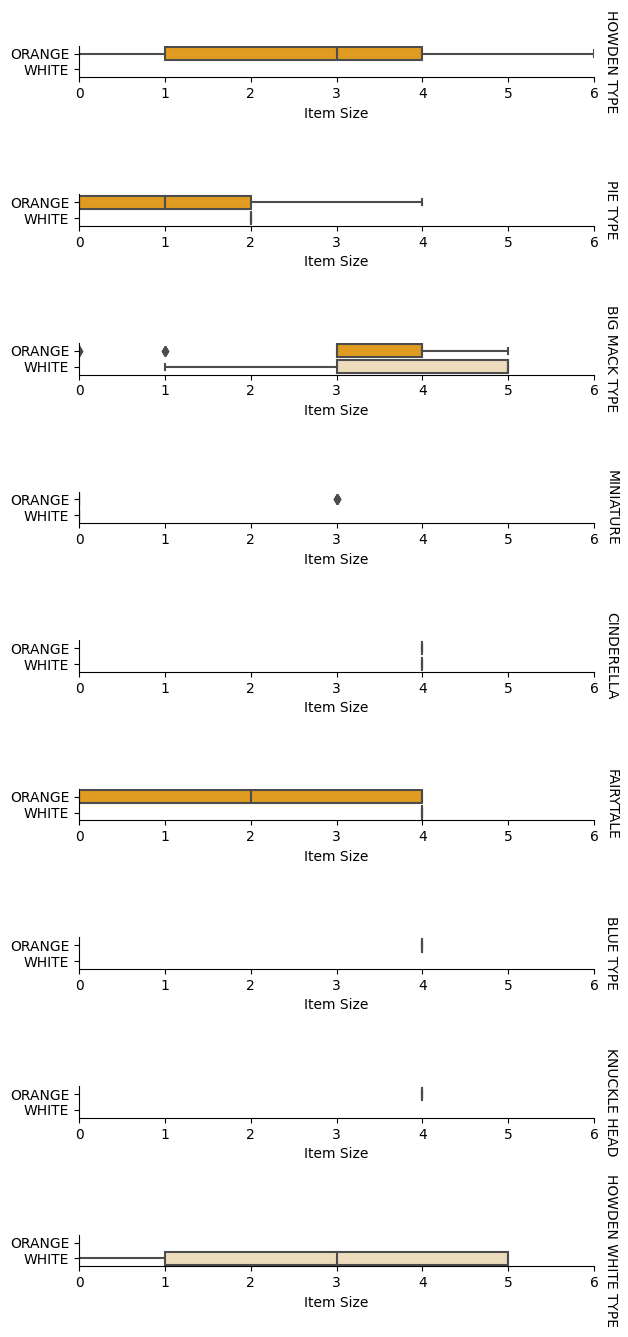
Nu hvor vi har forbehandlet vores data, kan vi analysere forholdet mellem funktionerne og labelen for at få en idé om, hvor godt modellen vil kunne forudsige labelen givet funktionerne. Den bedste måde at udføre denne type analyse på er at plotte dataene. Vi bruger igen Seaborn-funktionen catplot til at visualisere forholdet mellem Item Size, Variety og Color i et kategorisk plot. For bedre at plotte dataene bruger vi den kodede Item Size-kolonne og den ukodede Variety-kolonne.

    palette = {
    'ORANGE': 'orange',
    'WHITE': 'wheat',
    }
    pumpkins['Item Size'] = encoded_pumpkins['ord__Item Size']

    g = sns.catplot(
        data=pumpkins,
        x="Item Size", y="Color", row='Variety',
        kind="box", orient="h",
        sharex=False, margin_titles=True,
        height=1.8, aspect=4, palette=palette,
    )
    g.set(xlabel="Item Size", ylabel="").set(xlim=(0,6))
    g.set_titles(row_template="{row_name}")

Brug et swarm plot

Da Color er en binær kategori (Hvid eller Ikke hvid), kræver det 'en specialiseret tilgang til visualisering'. Der er andre måder at visualisere forholdet mellem denne kategori og andre variabler.

Du kan visualisere variabler side om side med Seaborn-plots.

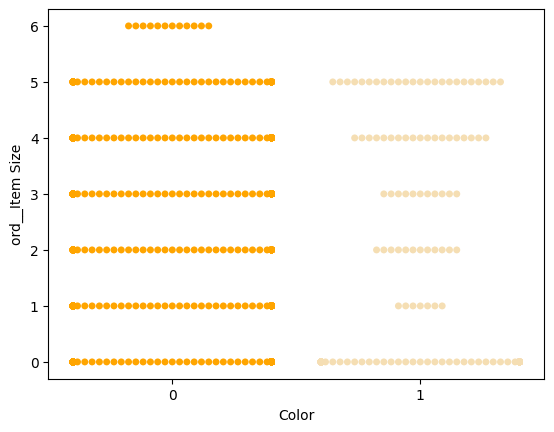
Prøv et 'swarm'-plot for at vise fordelingen af værdier:

palette = {
0: 'orange',
1: 'wheat'
}
sns.swarmplot(x="Color", y="ord__Item Size", data=encoded_pumpkins, palette=palette)

Pas på: Koden ovenfor kan generere en advarsel, da Seaborn har svært ved at repræsentere så mange datapunkter i et swarm-plot. En mulig løsning er at reducere størrelsen på markøren ved hjælp af parameteren 'size'. Vær dog opmærksom på, at dette påvirker læsbarheden af plottet.

🧮 Vis mig matematikken

Logistisk regression bygger på konceptet 'maksimal sandsynlighed' ved hjælp af sigmoid-funktioner. En 'Sigmoid-funktion' på et plot ligner en 'S'-form. Den tager en værdi og mapper den til et sted mellem 0 og 1. Dens kurve kaldes også en 'logistisk kurve'. Dens formel ser sådan ud:

hvor sigmoids midtpunkt findes ved x's 0-punkt, L er kurvens maksimale værdi, og k er kurvens stejlhed. Hvis resultatet af funktionen er mere end 0,5, vil den pågældende label blive givet klassen '1' af det binære valg. Hvis ikke, vil den blive klassificeret som '0'.

Byg din model

At bygge en model til at finde disse binære klassifikationer er overraskende ligetil i Scikit-learn.

🎥 Klik på billedet ovenfor for en kort videooversigt over opbygning af en lineær regressionsmodel

Vælg de variabler, du vil bruge i din klassifikationsmodel, og opdel trænings- og testdatasæt ved at kalde train_test_split():

from sklearn.model_selection import train_test_split

X = encoded_pumpkins[encoded_pumpkins.columns.difference(['Color'])]
y = encoded_pumpkins['Color']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Nu kan du træne din model ved at kalde fit() med dine træningsdata og udskrive resultatet:

from sklearn.metrics import f1_score, classification_report 
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)

print(classification_report(y_test, predictions))
print('Predicted labels: ', predictions)
print('F1-score: ', f1_score(y_test, predictions))

Tag et kig på din models score. Det er ikke dårligt, taget i betragtning at du kun har omkring 1000 rækker data:

                   precision    recall  f1-score   support

                0       0.94      0.98      0.96       166
                1       0.85      0.67      0.75        33

    accuracy                                0.92       199
    macro avg           0.89      0.82      0.85       199
    weighted avg        0.92      0.92      0.92       199

    Predicted labels:  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0
    0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
    0 0 0 1 0 0 0 0 0 0 0 0 1 1]
    F1-score:  0.7457627118644068

Bedre forståelse via en forvirringsmatrix

Mens du kan få en score-rapport termer ved at udskrive ovenstående elementer, kan du muligvis forstå din model lettere ved at bruge en forvirringsmatrix til at hjælpe os med at forstå, hvordan modellen klarer sig.

🎓 En 'forvirringsmatrix' (eller 'fejlmatrix') er en tabel, der udtrykker din models sande vs. falske positive og negative, og dermed vurderer nøjagtigheden af forudsigelserne.

For at bruge en forvirringsmatrix skal du kalde confusion_matrix():

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, predictions)

Tag et kig på din models forvirringsmatrix:

array([[162,   4],
       [ 11,  22]])

I Scikit-learn er rækker (akse 0) faktiske labels, og kolonner (akse 1) er forudsagte labels.

	0	1
0	TN	FP
1	FN	TP

Hvad sker der her? Lad os sige, at vores model bliver bedt om at klassificere græskar mellem to binære kategorier, kategori 'hvid' og kategori 'ikke-hvid'.

Hvis din model forudsiger et græskar som ikke hvidt, og det faktisk tilhører kategorien 'ikke-hvid', kalder vi det en sand negativ, vist ved det øverste venstre tal.
Hvis din model forudsiger et græskar som hvidt, og det faktisk tilhører kategorien 'ikke-hvid', kalder vi det en falsk negativ, vist ved det nederste venstre tal.
Hvis din model forudsiger et græskar som ikke hvidt, og det faktisk tilhører kategorien 'hvid', kalder vi det en falsk positiv, vist ved det øverste højre tal.
Hvis din model forudsiger et græskar som hvidt, og det faktisk tilhører kategorien 'hvid', kalder vi det en sand positiv, vist ved det nederste højre tal.

Som du måske har gættet, er det at foretrække at have et større antal sande positive og sande negative og et lavere antal falske positive og falske negative, hvilket indebærer, at modellen klarer sig bedre. Hvordan relaterer forvirringsmatricen sig til præcision og recall? Husk, at klassifikationsrapporten, der blev printet ovenfor, viste præcision (0.85) og recall (0.67).

Præcision = tp / (tp + fp) = 22 / (22 + 4) = 0.8461538461538461

Recall = tp / (tp + fn) = 22 / (22 + 11) = 0.6666666666666666

✅ Q: Ifølge forvirringsmatricen, hvordan klarede modellen sig? A: Ikke dårligt; der er et godt antal sande negative, men også nogle få falske negative.

Lad os genbesøge de begreber, vi så tidligere, ved hjælp af forvirringsmatricens kortlægning af TP/TN og FP/FN:

🎓 Præcision: TP/(TP + FP) Andelen af relevante instanser blandt de hentede instanser (f.eks. hvilke labels blev korrekt mærket)

🎓 Recall: TP/(TP + FN) Andelen af relevante instanser, der blev hentet, uanset om de blev korrekt mærket eller ej

🎓 f1-score: (2 * præcision * recall)/(præcision + recall) Et vægtet gennemsnit af præcision og recall, hvor det bedste er 1 og det værste er 0

🎓 Support: Antallet af forekomster af hver hentet label

🎓 Nøjagtighed: (TP + TN)/(TP + TN + FP + FN) Procentdelen af labels, der blev korrekt forudsagt for en prøve.

🎓 Macro Avg: Beregningen af de uvægtede gennemsnitlige metrikker for hver label, uden at tage højde for label-ubalance.

🎓 Weighted Avg: Beregningen af de gennemsnitlige metrikker for hver label, hvor der tages højde for label-ubalance ved at vægte dem efter deres support (antallet af sande instanser for hver label).

✅ Kan du tænke på, hvilken metrik du bør holde øje med, hvis du vil have din model til at reducere antallet af falske negative?

Visualiser ROC-kurven for denne model

🎥 Klik på billedet ovenfor for en kort videooversigt over ROC-kurver

Lad os lave endnu en visualisering for at se den såkaldte 'ROC'-kurve:

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

y_scores = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])

fig = plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()

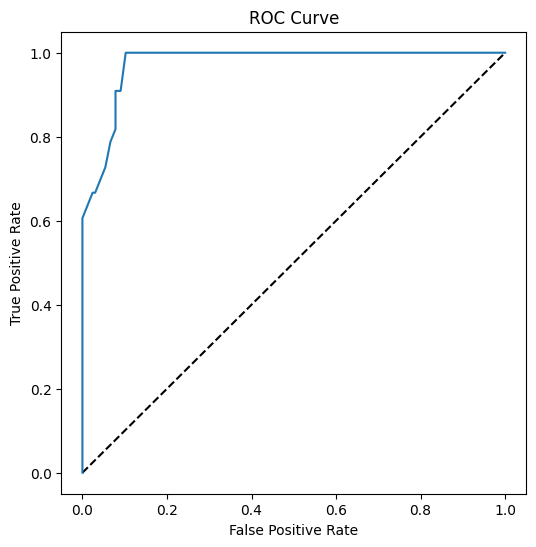
Ved hjælp af Matplotlib kan du plotte modellens Receiving Operating Characteristic eller ROC. ROC-kurver bruges ofte til at få et overblik over en klassifikators output i forhold til dens sande vs. falske positive. "ROC-kurver har typisk den sande positive rate på Y-aksen og den falske positive rate på X-aksen." Derfor betyder kurvens stejlhed og afstanden mellem midtlinjen og kurven noget: du vil have en kurve, der hurtigt bevæger sig op og over linjen. I vores tilfælde er der falske positive til at starte med, og derefter bevæger linjen sig op og over korrekt:

Til sidst kan du bruge Scikit-learns roc_auc_score API til at beregne den faktiske 'Area Under the Curve' (AUC):

auc = roc_auc_score(y_test,y_scores[:,1])
print(auc)

Resultatet er 0.9749908725812341. Da AUC spænder fra 0 til 1, vil du have en høj score, da en model, der er 100% korrekt i sine forudsigelser, vil have en AUC på 1; i dette tilfælde er modellen ret god.

I fremtidige lektioner om klassifikationer vil du lære, hvordan du kan iterere for at forbedre modellens scores. Men for nu, tillykke! Du har gennemført disse regression-lektioner!

🚀Udfordring

Der er meget mere at udforske omkring logistisk regression! Men den bedste måde at lære på er at eksperimentere. Find et datasæt, der egner sig til denne type analyse, og byg en model med det. Hvad lærer du? Tip: prøv Kaggle for interessante datasæt.

Quiz efter lektionen

Gennemgang & Selvstudie

Læs de første par sider af denne artikel fra Stanford om nogle praktiske anvendelser af logistisk regression. Tænk over opgaver, der er bedre egnet til den ene eller den anden type regression, som vi har studeret indtil nu. Hvad ville fungere bedst?

Opgave

Prøv denne regression igen

Ansvarsfraskrivelse:
Dette dokument er blevet oversat ved hjælp af AI-oversættelsestjenesten Co-op Translator. Selvom vi bestræber os på nøjagtighed, skal du være opmærksom på, at automatiserede oversættelser kan indeholde fejl eller unøjagtigheder. Det originale dokument på dets oprindelige sprog bør betragtes som den autoritative kilde. For kritisk information anbefales professionel menneskelig oversættelse. Vi påtager os ikke ansvar for eventuelle misforståelser eller fejltolkninger, der opstår som følge af brugen af denne oversættelse.